基于无标度网络的公交线路优化设计
陈龙 姚鸿飞 倪辰中 郁鑫斐 林启哲


摘 要:公交网路设计是解决城市公交网络的关键环节,需要在设计阶段充分考虑公交站点和线路的性质,利用复杂网络理论针对公交需求的变化提供相应的需求,加大公交覆盖范围,提高城市公交的分担率及其可持续发展。本文充分考虑公交站点和线路的性质,利用复杂网络理论针对公交需求的变化提供相应的需求,加大公交覆盖范围,提高城市公交的分担率及其可持续发展。依托复杂网络理论,将复杂网络与公交规划相结合,提出了解决线路规划矛盾问题的方法,并考量了公交站点分布度数及热力度等权重因素,对公交站点种类进行划分。通过研究利用BA无标度网络模型,在已有的数据上设计了一套合理的网络生成算法,探讨了南京市栖霞区部分公交网络的设计方法。分析了BA无标度网络的特征,应用BA无标度网络的理论设计并生成了南京市栖霞区部分公交网络。
关键词:无标度网络 拓扑性质 线网优化 加权网络 城市公交
中图分类号:O29 文献标识码:A 文章编号:1674-098X(2021)04(c)-0012-06
Optimal Design of Bus Routes Based on Scale Free Network
—— A Case Study of Qixia District, Nanjing
CHEN Long* YAO Hongfei NI Chenzhong YU Xinfei LIN Qizhe
(Nanjing University of Finance and Economics, Nanjing, Jiangsu Province, 210023 China)
Abstract: The design of public transport network is the key to solve this contradiction. In the design stage, we need to fully consider the nature of bus stops and routes, use complex network theory to provide corresponding demand for the change of public transport demand, increase the coverage of public transport, and improve the sharing rate of urban public transport and its sustainable development.In this paper, we fully consider the nature of bus stops and routes, use complex network theory to provide corresponding demand for the change of bus demand, increase the coverage of bus, improve the share rate of urban bus and its sustainable development. Based on the complex network theory, this paper combines the complex network with the public transportation planning, puts forward the method to solve the contradiction problem of route planning, and considers the weight factors such as the distribution degree and thermal degree of public transportation stations, and divides the types of public transportation stations.Based on the BA scale-free network model, this paper designs a set of reasonable network generation algorithm on the existing data, and discusses the design method of part of the public transport network in Qixia District of Nanjing City. This paper analyzes the characteristics of BA scale-free network, and applies BA scale-free network theory to design and generate part of the bus network in Qixia District of Nanjing City.
Key Words: Scale free network; Topology property; Line network optimization; Weighted network; Urban public transport
城市公交網络的矛盾性表现在高速发展的城市建设、快速增加的城市人口与落后的城市传统出行交通的线路规划之间的复杂关系。因此公交线路的合理设计应当与时俱进,优化公交线路网成为当下热点话题,也响应“十四五”的公交设计政策,以南京市栖霞区为例优化了公交线路,以期提高社会公共资源的利用效率,节约公交企业运营成本。
1 研究背景及研究意义
1.1 研究背景
城市公交网络的矛盾性表现在高速发展的城市建设、快速增加的城市人口与落后的城市传统出行交通的线路规划之间的复杂关系。然而在大部分城市中,城市公交网络无法解决类似的矛盾。当今城市的公交站点性质和公交线路性质多为静态,造成了公交系统供给侧需求不平衡的局面,严重影响了公交系统的有效性。
公交网路设计是解决这一矛盾的关键环节,首先要广泛地采集信息,利用信息分析站点和线路的性质,利用復杂网络理论对公交进行供给侧结构性改革。从现有阶段看,需求的变化是复杂网络理论应用于公交网络设计最重要的一环。
1.2 研究意义
目前对于公交网络的优化方案中很少从复杂网络的节点影响力的角度,来对公交网络中的站点进行深入研究。但在复杂网络视角下进行拓扑分析时,我们可以通过静态指标和动态指标来对整个网络进行分析。这两类指标分别对应的是结构和功能两个维度,会使得操作后的分析结果直观而全面。建立一套站点分类分级体系,会大大提高公交网络的供给能力,并且提高社会公共资源的利用效率,节约公交企业运营成本。
2 国内外研究现状
2.1 国内研究现状
国内关于交通建设的研究起步较晚,公交线网设计的方法主要有优化成网法、逐条布设、分层布设法以及全局最优法等4种算法。其中逐条布设、优化成网法最早由韩印(1994)提出,使用简便的优化算法,建立一系列的备选线路,并将其逐次累加在线路网上[1]。这些方法的优点是避免了公交线路中维数混乱问题。
分层布设法最早由陆建等(2004)提出,以公交线路功能层次划分为依据提出了线网层次规划设计法。通过分层赋予城市线网不同的性质,建立相应的优化网络模型,运用线性规划的多目标优化算法以此来便可获得最优结果[2]。
全局最优法方面,王志栋(1997)运用线路重复系数、线网覆盖率等数据,以公交线路网整体效率建立了线网优化设计的非线性0-1规划模型,综合了考虑公交的经济利益和社会效益[3]。陈洪仁等(2000)学者则以优化出行时间和公交投入作为研究的目标,研究的过程用了遗传算法求解该模型的方法[4]。
2.2 国外研究现状
国外发达国家的交通建设起步较早,对公交线路的研究已经形成了较为成熟的理论体系。
在线路设计方面,学者Hurdle(1973),Kuah(1988)对公交站点选取,客流需求分布等方面进行了初步的研究,但并没有形成系统的理论体系[5-6]。Pattnaik(1998)第一次在公交线路网设计方面运用了遗传算法,建立了公交线网设计模型[7]。进入21世纪,Gallo(2011)和Sivakumaran(2012)在考虑乘客的时间成本和车辆使用成本的基础上,使用蚁群算法建立最优线路模型[8-9]。
2.3 国内外研究的不足之处
国内外一般将公共交通出行需求视为单一的固定值,然后根据单一的公共交通需求矩阵设计并生成合理的公共交通网络。这样做的最大问题是忽略了公交需求随时间变化的性质,因此难以在公交线网中实际发挥优良的作用。
尽管现代大数据技术以及数理统计模型分析技术已经开始逐步被应用于区域性公交线路的设计,但都是聚焦于公交网络的线路性质,缺乏对站点性质的研究。
复杂理论在航运、互联网、电力等方面的应用,已经体现了复杂网络理论的应用价值,有效地提升了上述领域供给侧结构性改革,以及供给侧对需求侧的应变[10]。但该理论目前尚未系统性地应用于公交设计方面。
3 公交站点设计思路
复杂网络模型中邻接矩阵法的引用,可以计算出一种缩减乘客乘坐时间与换乘时间的站间距优化模型。同时,国内一些城市的公交站点设计思路还可以看到交通流返回波动理论的影子,这让公交车的停靠对城市整体车流的影响控制在了一个可以接受的范围,这让公交停靠站的位置分布更加合理[11-12]。在复杂网络模型视角下,这对中途停靠站的站距有着重大意义。换乘枢纽站承担着吸引与辐射的双重职能,需综合考虑市内外客运系统和客流流量及流向分布,以期达到枢纽成最佳布局吸引客流的作用[13]。
4 公交站点分级制度
一方面考察公交站点在路网空间的通达性,另一方面考察公交站点的客流量即站点承载压力情况,将通达度高、承载压力较强的一类站点(即吞吐客运量较大,一般为城市枢纽),作为关键节点有针对性的集中考察和优化,对各站点的承载压力与通达度进行可视化处理,即用数学模型评估这两项标准后,对其进行赋权,加权计算后以数字的形式反映其首位度,并以此为依据进行分级。
建立了基于邻接站点表示方法的南京市栖霞区公交网络模型如图1所示,图中网络节点代表站点,同一线路上的相邻两个站点有一条连边。
表1中列出了南京市栖霞区公交网络中部分站点,节点度的统计情况,其中节点度为0的站点,并不是由于该站点的吞吐量为0,而可能是由于该站点的终点,始发站两者的位置不同造成的。南京市栖霞区公交网络站点度的均值为5.3,说明平均每个站点经过5辆公交车。同时站点度小于5的站点最多,占比为80.5%。说明绝大多数的站点的度往往都比较小,并且只有极少数的站点可以具有不可替代的连接枢纽作用。
根据站点附近客流量热力图及站点在公交网络中的度数进行赋权计算后,对于高频站点应着重强调站点综合调度能力,可适当增加班次来缓解此类站点承载压力,做到站点节度与所承载压力程度的匹配。对于中低频站点,则更应该注重以该站点为中心的覆盖面积,更好的服务居民出行。
5 基于无标度网络的城市公交网络设计
在我们认知中城市公交系统中往往都存在着的拥挤效应问题,即当城市公交系统的供给能力与人们的出行需求不匹配,从而造成了某个某一段的拥挤问题。就目前国内外的研究该问题的解决方式而言,主要有两种手段:一方面探寻如何加强城市公交系统供给量,但是这样一来消耗了社会众多资源,造成浪费,带来了一定的财政负担,并且方法未必有效;另一方面是分析现有公交系统中的客运量和公交系统运营效率,进而运用改进提高公交系统的运营效率,这样的方法看似有效,缓解了公交网络的拥挤问题,然而并未从根源上解决问题,整体上的系统仍是拥挤的[14-15]。
本文研究公交网络的拓扑性质与分析,充分利用社会资源,从而使得网络拓扑结构最优化,缓解城市拥挤问题,并以南京市栖霞区为例进行设计。
5.1 网络结构、容量的关联性分析
在日常的城市公交网络中,拥挤效应是一个重要特性,会使得公交系统的服务效率、承载能力急剧降低[16]。研究复杂网络特性,拓扑结构是基础,任何网络结构都有其最大的存储量,并且综合了动力学过程及动态特征与网络的拓扑结构密切相关,因此希望能够寻找最有公交網络结构,使得公交网络容量达到最大化的目的。
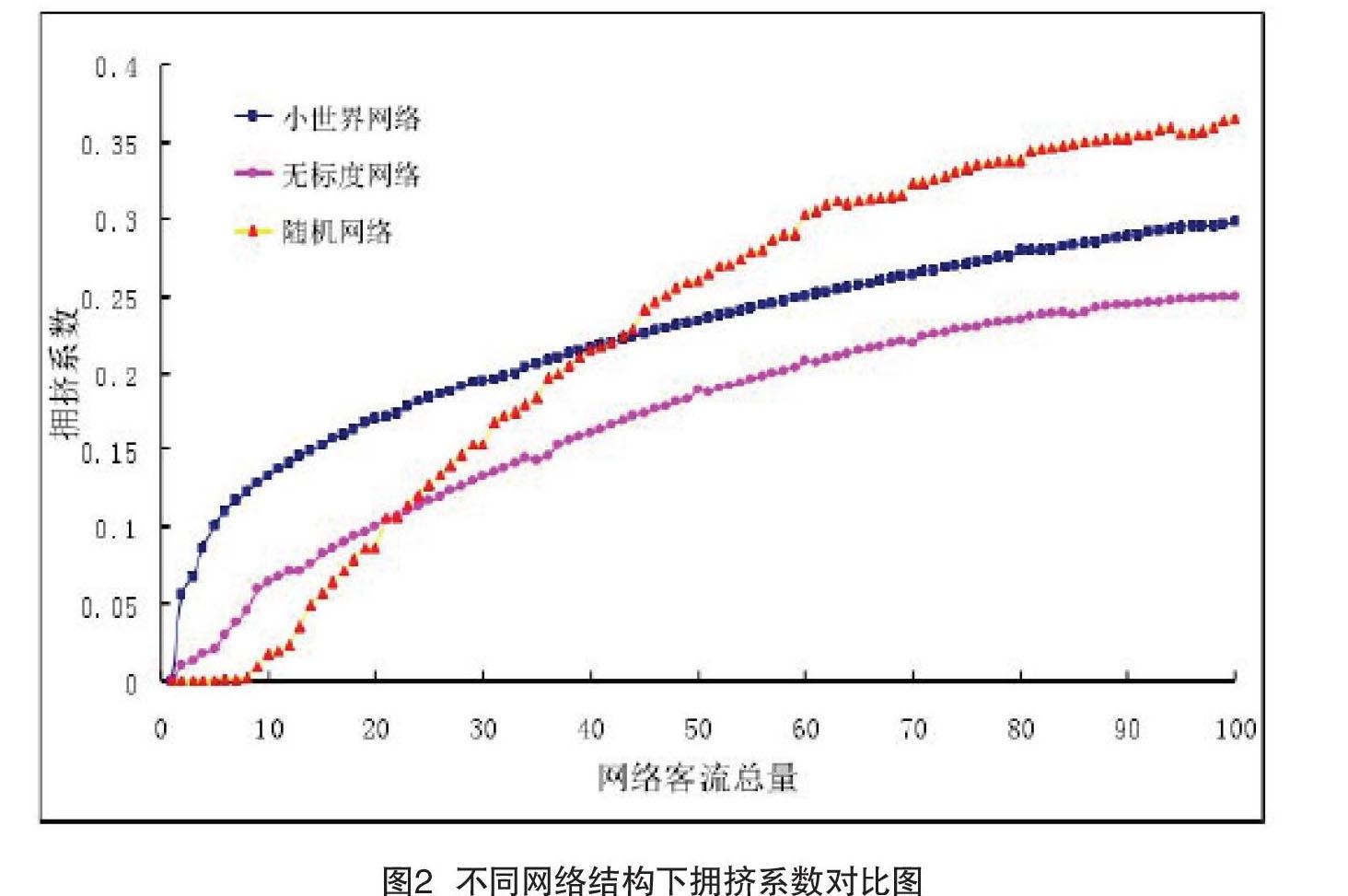
众多学者研究了网络模型、拓扑结构之间的关系。具体为生成节点总数N=400,节点平均度k=4的随即网络模型、小世界网络模型和无标度网络模型,其中无标度网络分布指数λ=2.5,随即网络的连接概率和小世界网络的重连概率都为p=0.1,按照边介数的大小分配最大容量C,当实际客运量超过C时则发生拥挤。图2是在仿真环境3种复杂网络拓扑结构中网络客运量与拥挤系数的关系图,其中拥挤系数为网络中发生拥挤的边数与网络中总边数的比值。
为了解决城市公共交通网络中的拥挤问题,设计了基于无标度网络拓扑结构的城市公共交通网络,使城市公共交通网络的容量最大化。通过对公交网络中边缘度大、节点度大的关键站点及其路径进行优化,可以有效地减少拥挤现象。
5.2 基于BA无标度网络模型的公交网络算法
复杂网络结构有两个重要特性:增长性和偏好连接性,即网络的规模是不断扩大的且新的节点更倾向于连接那些具有较高连接的节点[17-18]。
基于BA无标度网络模型的公交网络生成算法基本步骤如下:
(1)增长。选取m0个站点的初始公交网络开始,确定线路的首末站点集合,向网络中逐步引入新的站点,与网络中已存在的m个站点产生连边,这里m≤=m。
(2)优先连接。新加入的网络站点i以大小为Pi的概率与已经存在的站点j产生连接,其概率Pi的计算公式如下:
(1)
其中aij表示i与j之间的道路限制系数,Fij可以表示i站点与站点之间的相互引力,其计算公式如下:
(2)
其中Si、Sj,表示站点i与站点j的节点强度,k表示比例系数,f(Rij ,RjD)表示站点间的阻抗函数。
6 南京市栖霞区公交网络的设计与生成
本文以南京市栖霞区南京财经大学周边公交网络为例,验证BA无标度网络算法。图3为南京市栖霞区南京财经大学周边公交网络示意图,按照公交网络生成算法的基本流程,对南京市栖霞区南京财经大学周边公交网络进行设计,具体步骤如下。
(1)选取南京市栖霞区南京财经大学周边20条公交线路的始末站点及中间站点,两两组合,循环操作直到首末站点全部生成完毕,由此可以生成大约140种站点设计方案。
(2)旧站点Vn与网络中的新站点Vi按照偏好连接的原则进行连接,同时二者之间必须存在可达路径,循环操作,逐步增加网络规模。新点与旧点之间偏好连接的概率为两点之间的引力与旧点与周围所有已连接站点的引力和的比值,如公式所示:
(3)
其中,Πi表示已有站点Vn与新加入站点Vi之间产生连边的概率,值为0表示两站点之间不可能产生连边。bni表示两点之间的道路限制系数。Fni表示两点之间的引力。
(3)比较各个线路之间的优劣,将性能最优的20条备选线路布设在路网中。
该算法最终设计并生成了无标度网络结构的城市公交网络。表1是基于BA无标度网络生成算法所搭建的南京市栖霞区南京财经大学周边公交网络的基本信息,图4给出了140条备用线路集合构成的公交网络度分布情况,使用最小二乘法,回归方程可写为y=-2.6583x+0.764,故该公交网络度分布满足幂指数约为-2.58的幂率分布。
7 结语
本文充分考虑公交站点和线路的性质,利用复杂网络理论针对公交需求的变化提供相应的需求,提高城市公交的分担率及其可持续发展。以科学有效的复杂网络理论为依托,并考量了公交站点分布度数及热力度等权重因素,对公交站点种类进行划分。
利用公交网络生成算法,确定了无标度网络结构是解决南京市栖霞区公交网络拥挤问题的最优网络结构,分析了BA无标度网络的特征,设计并生成了南京市栖霞区部分公交网络。
公共交通对一个地区的经济具有着先导性、基础性、战略性的重要作用。进行公交网络优化,必须树立先进的系统观念,目光要具有前瞻性,谋划要具有全局性,布局要具有战略性,并且要在整体的层面上进行推进。在复杂网络网络模型的视角下,线路性质和站点性质是当今城市公交网路的两大显著特征。在这个时代背景下,该项目组响应“强富美高”的新南京建设愿景,也将根据“十四五”规划内容及时调整研究思路,确保研究成果更具实际意义和时代意义。
参考文献
[1] 钱蕾,韩印,姚佼.基于改进K-Means算法的交叉口影响路段行程速度估计[J].公路交通科技,2017,34(12):115-122.
[2] 陆建,王炜.城市交通系统可持续发展保障体系研究[J].城市交通,2004(3):10-13.
[3] 林开春.基于复杂网络的城市公交网络分析与优化[D].青岛:青岛大学,2018.
[4] 赵莉莉.复杂网络理论在城市公交系统中的应用[D].石家庄:河北师范大学,2010.
[5] Watts D J, Strogatz S H. Collective dynamics of |[lsquo]|small-world|[rsquo]|networks[J]. Nature, 1998, 393:440-442.
[6] Barabási A. Emergence of scaling in complex networks[M]// Handbook of Graphs and Networks: From the Genome to the Internet. Wiley‐VCH Verlag GmbH & Co. KGaA,2011:69-84.
[7] Yu B, Sun P, Chen T, et al. Confinement-induced novel morphologies of block copolymers.[J]. Physical Review Letters, 2006, 96(13):138306.
[8] 许丹,李翔,汪小帆.复杂网络病毒传播的局域控制研究[J]. 物理学报, 2007,56(3):1313-1317.
[9] Gattuso D, Miriello E. Compared Analysis of Metro Networks Supported by Graph Theory[J]. Networks & Spatial Economics, 2005, 5(4):395-414.
[10] 孙庆军.基于公交需求变化的柔性公交线网设计[D].哈尔滨:哈尔滨工业大学,2015.
[11] 狄兆华.基于复杂网络的城市公交网络拓扑特征及线路连通性分析[D].成都:西南交通大学,2015.
[12] 张枭.多模式公交拓扑网络构建及可达性评价研究[D].哈尔滨:东北林业大学,2019.
[13] 王非.基于复杂网络的公交线网特性分析与优化研究[D].北京:北京交通大学,2020.
[14] 冷順多.城市公共交通网络时间空间可达性模型研究与应用[D].北京:北京交通大学,2020.
[15] 魏超.城市轨道交通接驳公交线路设计问题[D].合肥:合肥工业大学,2015.
[16] 张君超.基于复杂网络的城市公交网络特性分析与演化研究[D].成都:西南交通大学,2010.
[17] 岳自豪.基于多模式分析的公交站点选址可视化系统设计与实现[D].杭州:浙江工业大学,2020.
[18] 王薇,王清华,郭明凤,等.城市定制公交线路及站点设计[J].中国市场,2019(27):120-121.

