基于参考依赖理论的出行者路径选择模型研究

赖元文，胡 亮，林 力,3

(1. 福州大学 土木工程学院，福建 福州 350116; 2.中交公路规划设计院有限公司，北京 100088；3.福建省交通规划设计院有限公司，福建 福州 350004)

0 引言

城市经济的快速增长，使得越来越多的人把汽车作为主要的交通方式，带给人们便利出行的同时，也导致了城市道路交通拥堵问题日益加剧。缓解城市交通拥堵，最关键的是从需求角度考虑，充分研究交通需求的本质。从微观角度，交通需求就是个体的择路行为，个体的出行路径选择行为集聚在宏观上表现为网络交通流的演化。这就要求我们深入探究出行者的路径选择行为的内在规律，用科学合理的模型来描述出行者的路径选择行为，从而能够预测城市交通状态、制订有效的交通控制诱导策略。传统的交通出行路径选择行为研究是以期望效用理论作为指导，理论的前提假设是个体选择行为只和当前状态有关，所建立的模型没有考虑个体决策特征。而参考依赖理论认为人们的决策行为不仅取决于备选方案的当前状态，而是将方案结果相对于参考点的相对值作为度量的标准。

参考点依赖理论最先应用于金融经济学领域的研究，之后才渐渐延伸至确定情境下的交通出行行为研究。Katsikopoulos等[1]采用行为学的实例验证方式揭示了出行选择行为中的参考点依赖特征。Borger等[2]考虑出行决策中的出行时间和收费，提出边际递减的价值函数形式，建立了基于参考点依赖的路径选择模型，通过试验证明出行决策中的损失规避特征。Hess等[3]在其研究中以自由流时间、减速时间、出行成本和路段收费作为特征属性，价值函数采用分段线性递减的形式，建立出行者路径选择模型。研究结果表明并非所有的出行特征属性都存在损失规避现象。范文博[4]在传统的出行路径选择logit模型中引入基于参考依赖的路径负效用，以此建立网络用户均衡模型，最后用相继平均法求解。研究结果表明出行者的参考点最终会跟随网络流量达到稳定状态。Lindsey等[5]提出出行者的出行效用由绝对效用和相对效用组成，绝对效用是指固有属性值带来的效用大小，相对效用是指与参考状态比较所得的收益-损失大小，并以此来研究道路拥挤收费问题。Delle等[6]考虑出行时间和拥挤收费的影响，以现状为参考点，建立参考点依赖下的多用户随机均衡模型。通过算例结果得出参考点依赖特性符合人们的实际出行行为，对路网的整体状态影响较大。Hjorth等[7]考虑出行时间和费用，重点研究出行者的时间价值，分析确定情境下时间价值对路径选择的影响。Li等[8]提出一种参考依赖下考虑异质性的均衡框架下的最优收费模型，最后使用基于遗传算法的解决方案来解决此优化问题。陈小君[9]将参考点引入旅行时间-运输费用的无差异曲线中，基于参考依赖理论对传统的时间价值模型进行改进，结果表明出行时间的损失规避程度要高于票价的损失规避程度。龚建[10]通过问卷调查，验证了在出行时间和拥挤收费两个属性上的参考依赖特征，提出多属性的出行决策模型。最后将系统出行时间最小作为目标，建立考虑拥挤收费的优化模型。徐红利等[11]考虑出行时间和拥堵收费两个属性，在确定性交通网络中建立了基于参考点依赖理论的出行路径选择决策模型，参考点的设置选取依据当前的出行时间和道路收费，研究表明以往的出行经验会影响路径选择的最后结果。娄路[12]建立了基于参考依赖理论的流量逐日演化模型，从出行者的心理角度出发，研究了参考点变动下的流量演化过程以及不同心态类型的出行者对应的路径选择对路网流量演化的影响。闫苗[13]同时考虑参考依赖和心理预算对路径选择的影响，在效用函数中选取出行时间和拥挤收费作为决策属性，建立了交通网络均衡模型，用于拥挤收费策略的研究。Avineri等[14]提出参考点的选取可以根据出行者的期望出行时间或者行程时间均值和中值，对每种情况下的异同点进行分析比较。Knetsch等[15]认为对于出行者而言可以将出行路径的自由流时间作为参照点。De Palma[16]和Kristensen H[17]等考虑影响参考点形成的多种因素，提出参考点可根据影响因素之间的关系来进行调整。

综合国内外研究现状可以发现，在运用参考依赖理论研究路径选择行为中，现在大多研究关注是路网均衡的分析，对交通系统的演化特征和规律研究不够深入，仅考虑路径属性因素的影响，忽略了出行者的行为特征，对出行者的决策理论缺乏行为学和心理学的理论基础和实证研究支撑。普遍将出行者视为群体，没有考虑个体异质性。在多属性路径选择决策问题研究方面，目前的研究侧重对各属性之间采用不同算法确定权重进行数理处理，没有从出行者的出行行为和出行决策心理角度考虑。

本研究旨在参考依赖理论的框架下围绕出行者路径选择问题展开深入研究，基于合理的行为假设解析出行行为发生的微观机理，运用参考依赖理论对传统路径选择模型进行改进和拓展，以期准确地反映出行者的路径选择行为特征和规律。

1 参考依赖决策过程

本研究中的出行者主要指有日常出行需求的私家车出行者。根据参考依赖理论，可以描述出行者的出行决策步骤如下：

(1)编辑阶段。出行者对本次出行的信息进行初步分析，并形成出行决策的参考点，参考点可以是内在的也可以是外在的。每条备选路径在每个属性上相对于该参考点分别会产生收益或者损失。

(2)评价阶段。对经过编辑阶段的路径信息进行评价，将各条备选路径在各个属性上的收益值和损失值分别赋予不同的权重。同等水平的收益与损失并不等效，损失会比等量的收益对出行者带来更大的心理效用。计算得出各条备选路径的参考依赖效用值，根据参考点的不同，效用值可正可负。

(3)选择阶段。根据出行效用的大小作出决策，效用值越高的路径被选择概率越大。

2 决策效用机制

假设效用函数U可以分解为单调且相互独立的出行时间效用函数F(T)和出行费用效用函数H(M)[9]。其中函数的自变量T和M分别为出行路径实际的时间长短和费用多少。根据出行特征，人们总是追求时间最少费用最小，所以时间效用函数和费用函数应均为单调递减函数。则可表示为：

U(T,M)=U[F(T),H(M)]。

(1)

由于假设的函数是可分解的，出行效用可用时间效用函数和费用效用函数的和来表示：

U(T,M)=F(T)+H(M),

(2)

F(T)=f(T)，

(3)

H(M)=h(M)。

(4)

在交通出行领域，常用的f(T)和h(M)函数形式有线性的、指数型的和幂函数型等，为方便分析研究，后续研究中时间和费用的效用函数采用线性形式。

根据参考依赖理论，可考虑将函数F(T)和H(M)替换为以(Tw，Mw)为参考点的效用函数，两个函数相互独立且单调：

(5)

(6)

对上式进行整理，可简化为：

U(i)=α(Tgi-λT·Tli)+β(Mgi-λM·Mli)，

(7)

式中，Tgi=max[Tw-Ti,0]；Tli=max[Ti-Tw,0]，Mgi=max[Mw-Mi,0]；Mli=max[Mi-Mw,0]。Tw和Mw分别为时间参考点和费用参考点；Tgi和Tli为路径i在时间属性上的相对收益和损失；Mgi和Mli为路径i在费用属性上的相对收益和损失；λT和λM分别为时间和费用的损失规避参数。

出行者选择路径i的概率为：

P(i)=prob(U(i)>U(j),∀i≠j)=

(8)

式中，P(i)为选择路径i的概率；j为任意备选路径。

3 问卷结构及内容

本研究采用SP调查方法，选择福州市的城区主要范围进行发放问卷，包括福州大学、东街口、五一广场、金山公园、宝龙城市广场和仓山万达广场6个区域，调查基本涵盖各个年龄段。调查共计发放问卷1 100份，通过初步整理筛选，剔除无效问卷124份，最终有效问卷976份，问卷有效率为88.7%。其中选择676份作为模型拟合数据，其余为模型验证数据。

在路径选择问卷中，备选路径的信息包括出行时间和出行费用组成(T,M)。如出行时间30 min，出行费用10元的路径K的基础信息可表示为：K(30,10)。正式问卷内容为：假设在一次出行中，给定两条备选路径信息A(30,5)和B(20,10)。首先在无参考点下，要求试验者根据两条路径的出行信息进行选择，得到选择路径A和路径B的比例。然后，给定一组参考点(Tw1，Mw1)，可解释为从出发点O到目的地D的历史出行经验，目的是为了提供给出行者一个参考状态，对行程有大概的心理认知。之后要求出行者根据本组参考点，重新在路径A和路径B中做选择。若不存在参考依赖特征，则选择路径A和路径B的出行者比例将不会发生太大变化。若存在参考依赖特征，则会出现两组试验者比例变化或逆转偏好。设置不同梯度的参考点，继续观察路径选择比例，可根据路径选择比例的变化探究出行者的选择行为特征。

不同参数取值下的路径状态如表1所示，根据出行时间和费用的不同组合，设置了9个参考点，如表2所示。

表1 不同参数取值下的路径状态Tab.1 Route states under different parameters

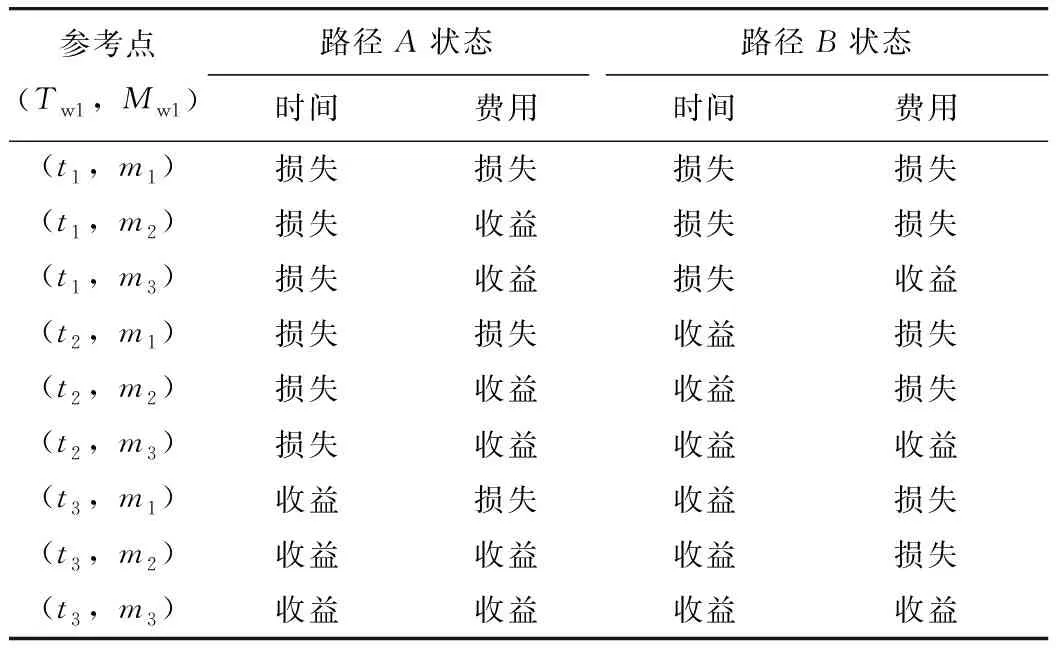
表2 不同参数取值组合下的路径状态Tab.2 Route states under different parameter combinations

时间价值判断问卷设计的主要内容为：假设日常出行中，从出发点O到目的地D，您经常选择的一条路径A出行时间为20 min，出行费用为10元。当您发现有另外一条路径B，B的出行时间为30 min，当出行费用M为多少时，您觉得这两条路径是没有太大差别，会在两条路径间自由选择切换。将出行者选择小于5的定义为高时间价值，大于等于5的定义为低时间价值。

对出行者进行划分之后，得出不同时间价值类型出行者在不同参考点下的路径选择结果，如表3所示。

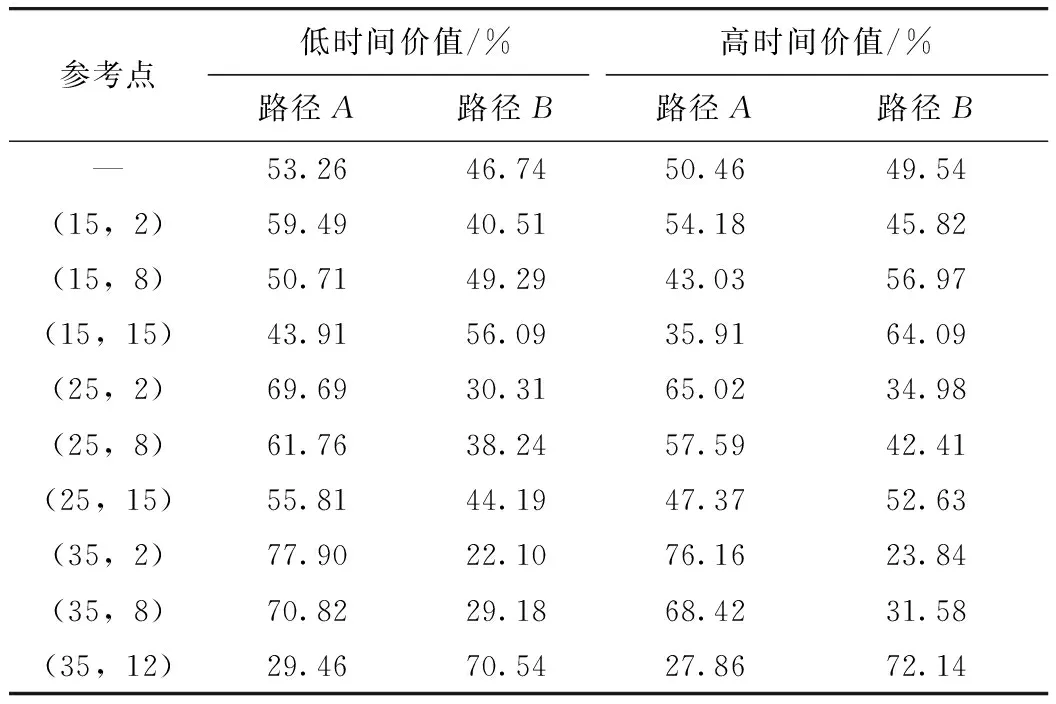
表3 不同时间价值类型出行者在不同参考点路径选择结果Tab.3 Result of route selection by travelers of different time value types at different reference points

4 参考依赖特征分析

以低时间价值类型的出行者数据为例分析。在无参考点下，根据logit模型，此时的路径选择比例为0.532 6∶0.467 4。在考虑参考点下，以参考点(15，2)为例，此时的路径选择比例为0.594 9∶0.405 1。选择比例发生变化，说明路径选择过程中存在参考依赖性，两条路径的效用发生了变化。

此外，从问卷数据中我们还可以观测到逆转偏好现象。在参考点(15，15)下，路径选择比例为0.439 1∶0.560 9，路径B的效用值超过了路径A。这是由于损失比等量的收益产生的心理效用更大，当参考点状态改变时，原来的收益可能变为损失，同理原本的损失也可能变为收益，这就使得效用函数大小发生改变，从而可能导致路径效用的差值发生符号变化，出现逆转偏好现象。

以两种类型时间价值的出行者在同一参考点下的路径选择结果来看，当参考点(25，8)时，低时间价值的出行者路径选择比例为0.617 6∶0.382 4，高时间价值的出行者路径选择比例为0.575 9∶0.424 1。说明同一参考点下，不同时间价值的出行者对同一出行路径的效用感知不同。在参考点(25，15)时，出现逆转偏好现象。

由此可得到，应用参考依赖理论能够对试验中的路径选择结果作出合理的解释，以此为基础建立路径选择模型是符合实际的，具有科学和试验依据。

5 参数标定与模型准确性验证

在利用问卷调查所得的数据，根据出行者的路径选择结果对考虑参考依赖的路径选择模型中的相关参数标定，并利用问卷预留数据进行模型的准确性验证。

本研究选用的方法为最小二乘法，通过构造平方损失函数，最佳参数值需要满足的条件是使所有数据组的残差平方和最小。一般求解方法为迭代法，对未知参数取偏导，通过迭代求得偏导数为0时的参数值。为提高迭代算法的收敛性，本研究拟采用遗传算法来求解。遗传算法是一种高效的全局搜索方法，能自适应地控制搜索过程以求得目标函数的最优解。

求解步骤如下，流程图见图1。

图1 遗传算法流程图Fig.1 Flowchart of genetic algorithm

(1)编码：为建立表现型和基因型的映射关系，需要“数字化”编码的方案。遗传算法运算时采用的是符号串，编码方式有二进制和浮点数；

(2)产生初始群体：通过随机的方法产生初始群体数据用来表示起始搜索点；

(3)适应度计算：每1条染色代表1个备选方案，适应性函数的大小体现了备选方案的优劣；

(4)随机算子：考虑随机因素，通过复制、交叉、变异3种方式产生新的个体。

(5)循环步骤3和4，终止条件根据目标函数要求或迭代次数确定，满足条件的参数即为最优解。

(9)

(10)

式中，U(Ak)为第k个参考点下路径A的效用值；U(Bk)为第k个参考点下路径B的效用值；Ak为第k个参考点下实际选择路径A的出行者比例；P(Ak)为第k个参考点下路径A的效用值大于路径B的效用值的概率。

用遗传算法估计参数α，λT，β，λM的取值过程中，算法的控制参数可取[18]：

(1)在模型中的符号已经代表收益和损失状态，故参数的取值范围均为正数：α>0，λT>0，β>0，λM>0；

(2)通过随机的方式产生个数为100的初始群体；

(3)将最小二乘法中构造的平方损失函数作为遗传算法的目标函数，即适应度；

(4)随机算子中，设定交叉概率为0.8，变异概率为0.01；

(5)当迭代次数达到200时，停止计算，得出所求解。

对不同类型时间价值出行者参考依赖效用函数中的α，λT，β，λM参数标定结果如表4所示。

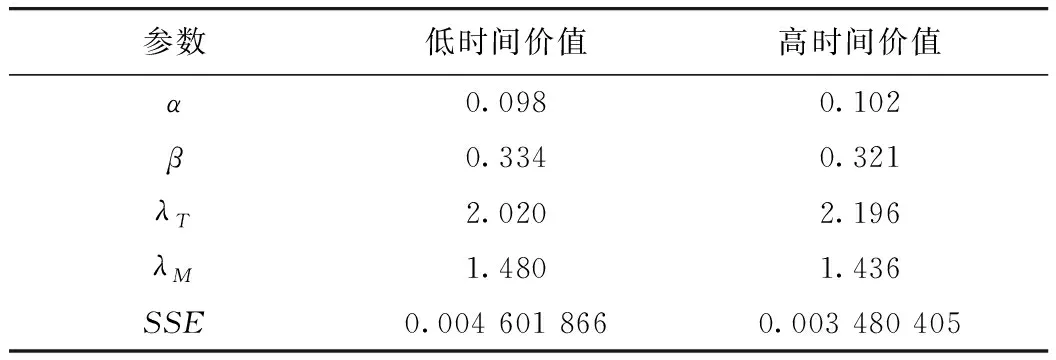
表4 基于参考依赖的路径选择模型参数标定结果Tab.4 Calibration result of route choice model parameters based on reference dependence

从总体来看，时间的损失规避参数λT和费用损失规避参数λM均大于1，说明出行者在时间属性和费用属性上都存在损失规避现象，损失会比等量的收益对出行者带来更大的心理效用。λT>λM说明出行者对于时间的损失规避程度要高于费用的损失规避程度，即出行者对时间损失的敏感性更高。虽然在费用属性上同样存在损失规避，出行时间的价值可以通过其与出行费用的替代关系来体现，而根据参考依赖理论人们在面对损失比收益时更敏感的心理，问卷调查分析中得出的出行时间损失的敏感性更高，在现实生活可表现为出行者对于不能准时到达目的地的厌恶程度比多花费出行费用的厌恶程度更高。

从两种类型出行时间价值的系数对比可以看出，高时间价值出行者的时间损失规避参数λT比低时间价值出行者高，说明了其对时间的要求更高，更加看重时间属性的收益损失，时间损失对其造成的影响作用较大。相应的，在费用属性上高时间价值出行者的费用损失参数λM会比低时间价值出行者低，说明相比于时间损失，费用的损失对其来说更容易接受，换句话来说愿意用更多的费用损失来换取时间上的较少量损失。

利用调查问卷的预留数据对模型的准确性进行验证，根据决策效用机制计算每条路径的理论效用值，得出理论路径选择比例，与实际调查结果进行对比，结果如表5和图2所示。

表5 实际调查结果与理论预测结果对比(以路径A为例)Tab.5 Comparison of actual survey result to theoretical prediction result (Take Route A for example)

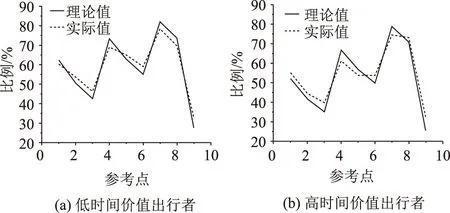
图2 不同时间价值出行者路径选择理论值与实际值对比Fig.2 Comparison of theoretical value to actual value of route choice for travelers with different time values

可以看出理论值与实际值之间的误差较小，根据参考依赖理论计算得到的理论值基本能反映出行者的实际路径选择情况，也验证了本研究模型的有效性。

6 模型使用范围及应用

本研究选取出行时间和费用作为路径选择的主要影响因素，以此建立基于参考依赖理论的路径选择模型。出行者根据选择具体某一条路径时在时间和费用属性上的收益和损失效用来作出决策，而收益损失是相对于时间和费用参考点的差值，这就使得出行者在作出出行决策时不仅考虑当前状态，还依赖于与参考点状态的比较。由于影响出行行为选择的因素众多，本研究提出的模型仅适用于多路径下出行时间和费用差异性较大的情况，假定各路径间其他影响因素情况较为接近。相比于个体决策行为只与当前状态有关的传统效用理论，考虑参考依赖理论的出行效用可以更加真实地反映人们的实际出行行为特征。

针对出行者的参考依赖特征，论文所提出的模型可以为交通管理部门提供交通管理策略，可通过向出行者提供带有路径参考点的信息，诱导人们的出行路径选择。

在实际出行中，无法获取每个出行者的出发地和目的地，可以以特定的路段区间作为调控的对象，针对易引起交通瓶颈的路段实施合理有效的诱导措施，缓解拥堵。具体思路为：

(1)针对某一相同起始点的几条可代替路径，根据实际的路况，获取相应的出行时间和出行费用。

(2)对于流量比较集中的路径要进行分流，让瓶颈路径的流量更加平均地分配到各条路径，以提高道路的总体通行效率。

(3)运用基于参考依赖理论的路径选择模型，以最后路径所要达到的理想流量为目标，反推所需的时间和费用参考点。

交通管理部门可通过广播或指示标志等途径将参考点传达到驾驶员，诱导驾驶员的路径选择，从而达到理想的网络状态。

7 结论

本研究在对出行者路径选择行为特征的研究基础上，建立考虑出行时间和出行费用的个体出行路径选择模型。通过对出行者进行SP调查，获取在不同参考点下的路径选择比例，分析不同时间价值类型出行者的路径选择行为差异。根据调查数据应用最小二乘法和遗传算法对不同时间价值出行者的收益损失参数进行标定并验证了模型有效性。

主要结论归纳如下：

(1)模型有效性。通过验证数据证明基于参考依赖理论所建立的出行路径选择模型具有有效性，可以进一步以参考依赖理论为框架研究出行者路径选择问题。

(2)出行者存在损失规避行为。模型参数标定中，出行者的时间损失规避参数和费用损失规避参数均大于1，说明出行者在时间属性和费用属性上都存在损失规避现象。对于出行者来说，同等数值的损失比同等收益带来的影响更大，出行者宁愿少获得一些收益，也不愿意承受损失的风险。

(3)时间价值影响出行路径选择。不同时间价值类型出行者有不同的损失规避系数，从而表现出不同的路径选择结果，高时间价值出行者的时间损失规避系数大于低时间价值出行者，费用损失规避系数则小于低时间价值出行者，即高时间价值出行者对于时间损失的重视程度更高，会选择高费用的路径来规避时间损失带来的效用。

(4)对所研究对象进行时间价值分类之后标定不同的模型参数能够较好地描述出行者的路径选择行为。