基于珠海万山定标场沿岸验潮仪的HY-2B雷达高度计定标研究

张宇飞，蒋兴伟，马超飞*

(1.国家卫星海洋应用中心，北京 100081)

1 引言

高度计从提出至今已有50余年，极大地促进了海洋科学、地球物理、大地测量等诸多领域的发展，其精度目前已经达到厘米级，能够很好地满足人们对海浪、海流等方面研究的需要。然而，高度计在对海面高度进行测量的过程中存在着偏差和偏移，其变量较多，不确定性较大，因此，高度计的数据产品质量需要严格的定标和验证来保证。卫星高度计的定标是指通过独立的方法，根据确定的受控信号（微波脉冲），定量地定义和比较测距系统的观测结果（海面高度）的过程。目前的高度计海面高度定标分为现场观测绝对定标与星星交叉相对定标，其中只有绝对定标能够给出绝对意义的高度计定标参数，反映真实的海面高度。

海洋二号B卫星（HY-2B）是我国第2颗海洋动力环境卫星，其于2018年10月26日发射。该卫星集主、被动微波遥感器于一体，具有高精度测轨、定轨与全天时、全天候、全球探测能力。雷达高度计是HY-2B最重要的一项载荷，其主要功能是用于测量海面高度、有效波高和海面风速，可用于重力场、全球流场等研究。

随着高度计定标需求日益增加，目前，国际上已经建成4个业务化高度计定标场。我国也由于HY-2系列定标需要，于珠海万山HY-2B的星下点附近建立了HY-2系列卫星高度计专用的定标场，目前，珠海万山定标场已经建设完成，主要设备布放于外伶仃岛、担杆岛、直湾岛和庙湾岛及周边海域。万山定标场位于HY-2B升轨轨道375与降轨轨道362交叉点附近。万山定标场目前布放有全球导航卫星系统（GNSS）浮标与永久性验潮站，除此之外，还建立了业务化运行的GNSS基准站，为验潮站提供水位基准，并为高度计定标提供湿大气路径延迟校正项。在HY-2B成功发射后，国家卫星海洋应用中心立即于2018年11−12月开展了HY-2B的在轨测试试验，于珠海万山定标场使用GNSS浮标与沿岸验潮仪进行了HY-2B雷达高度计定标检验试验。本文主要使用试验中的沿岸验潮仪数据，对我国HY-2B雷达高度计进行了初步定标工作。

2 高度计测高与定标

高度计测高测量的是卫星的高度计到星下点海面的距离。其观测过程可简述为高度计向星下点海面发射一束短微波脉冲，脉冲与海面相互作用，部分脉冲被粗糙的海面反射回高度计，高度计以发射脉冲与接收脉冲回波的时间差测量星下点足印内的平均海面高度。其计算公式如下式所示：

高度计作为一个精密的主动式微波雷达，其在对海面高度进行观测的过程中会受到诸如仪器误差、轨道误差、测距误差、地球物理误差等几个方面的影响。除地球物理误差外，其余3项均会直接影响高度计测距，地球物理误差的影响体现在计算海面动力地形高度时的偏差。因此，式（1）中的距离 R在对高度计进行绝对定标前，需要对上述地球物理误差以外的误差项进行校正。如果GNSS基站对坐标进行解算时去除了地球物理误差，则需要在高度计对海面高度进行计算时予以去除。进行误差校正后，高度计测得的海面高度如下式所示[1]：

式中，S SHalt为进行误差校正后的高度计测量的海面高度；halt为卫星高度计距参考椭球面的轨道高度；Rcorr为校正仪器误差、轨道误差与测距误差后高度计到星下点海面的距离；t idecorr为地球物理误差校正项。经过误差校正后，高度计到星下点海面的距离如下式所示[1]：

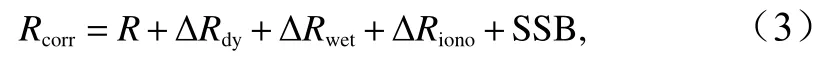
式中，R为与式（1）相同的测距误差校正前高度计距离测量值，其余各项均为测距误差校正项，包含干大气延迟校正 ∆Rdy、湿大气延迟校正 ∆Rwet、电离层延迟校正 ∆Riono与 海况校正 S SB。

地球物理误差校正项tidecorr如下式所示：

式中，∆Rsolid为地球固体潮；∆Rloading为负荷潮；∆Rpole为极潮。卫星高度计的绝对定标原理可以做如下解释：通过现场观测，在卫星星下点处、卫星过境时刻测量的海面绝对高度值，与卫星高度计星上测量的海面高度进行对比，二者对比的结果即为高度计的偏差或偏移（Bias）[2]，表达形式如下式所示：

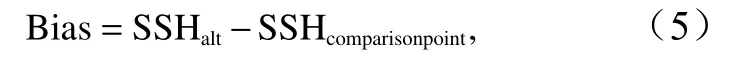
目前通用现场外定标，基本的方法大致有下列4种：（1）通过在星下点布放的GNSS浮标直接对海面高度进行测量[4]；（2）通过星下点离岸锚系压力验潮仪与GNSS浮标进行同步观测；（3）利用沿岸的验潮仪进行水位测量，再通过模型将沿岸水位外推至星下点；（4）通过陆上布放的有源定标器进行卫星高度计测距精度定标。其中，使用沿岸验潮仪进行的高度计定标方法仪器布放简单且便于维护，能够大范围布放，适合作为定标场长期业务化运行的主要测量手段[5]，也是本文对HY-2B进行绝对定标所使用的方法。

3 基于万山定标场沿岸验潮仪的HY-2B雷达高度计定标试验

高度计的绝对定标参数由现场观测数据与星上观测数据两部分组成。本节将分别对万山定标场HY-2B定标试验中这两部分数据的获取进行详细论述，并最终得到HY-2B雷达高度计在轨测试期间通过沿岸验潮仪计算得到的绝对定标参数。

3.1 通过沿岸验潮仪获取 SSHtg

通过上述方法，沿岸验潮仪现场观测获得的星下点海面高度如下式所示[8]：

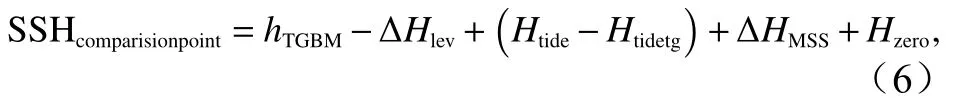
式中，SSHcomparisionpoint为间接测量的星下点海面高度；hTGBM为GNSS基站相对参考椭球面的高度；∆Hlev为GNSS基站与验潮仪0点的高度差；Htide为星下点处潮高；Htidetg为验潮仪处潮高；∆Hmss为验潮仪处与星下点处的平均海平面高度之差；Hzero为压力验潮仪0点至海面的水位高度，即验潮仪测量的瞬时水位变化。

本次HY-2B的定标试验在珠海万山定标场的直湾岛共布放了3个沿岸验潮仪，3个验潮仪均布放在定标场的同一经纬度坐标位置，使用与HY-2B相同的T/P参考椭球体。验潮仪中有2个布放在水下，1个布放在水面上用以进行大气校正，只有水下验潮仪记录了水位信息。验潮仪布放时间为2018年11月3日至12月12日，在此期间，HY-2B共经过验潮仪所在位置附近的星下点3次，分别为UTC时间11月12日、11月26日和12月10日的10时08分前后。经过比对，两个布放在相同位置的水下验潮仪在校正高程基准后测量结果一致，只使用其中的一个水下验潮仪进行定标即可。验潮仪具体参数如表1所示。

表1 万山定标场验潮仪位置与试验时间Table 1 Position and time of tide gauge experiment in Wanshan calibration site

水下验潮仪所记录的水位信息为验潮仪距离瞬时海面的距离，使用验潮仪观测的水位需要根据GNSS基站测量的验潮仪的高程转换为海面高度，如下式所示：

式中，SSHtg为验潮仪所测的海面高度，其余各项与式（6）中的各项含义一致。经过高程基准校正后，验潮仪试验测得的HY-2B过境当日的海面高度与过境时刻（北京时间）的海面高度如图1所示。

图1a至图1c分别为HY-2B周期001、周期002与周期003过境当日，万山定标场验潮仪所测量的海面高度变化。其中，曲线为海面高度变化的300 s滑动平均，用于消除海面的随机信号，测量频率为1 Hz，每日共测量86 400个海面高度数据。直线表示HY-2B经过星下点所对应的当地时间。二者的交点即为验潮仪所测的海面高度SSHtg。

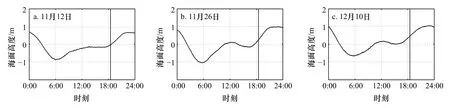
图1 验潮仪测量的海面高度与 HY-2B 过境时刻Fig.1 Sea surface height from tide gauge and HY-2B passing moment

3.2 通过 SSHtg计算 SSHcomparisionpoint

沿岸验潮仪所测量的海面高度并非星下点的海面高度，因此需要将海面高度通过式（6）将验潮仪处的海面高度外推至星下点。

HY-2B在经过万山定标场附近时会产生数个星下点足印，通过对比这些不同星下点的定标参数，可以研究高度计定标参数的变化趋势。在星下点的选择上，与验潮仪的距离范围选取不应过大也不应过小。选取范围过大时，除了潮汐与大地水准面的差异，还会产生其他误差，诸如地转流与中尺度涡的影响，不便于进行潮汐外推工作。在选取范围过小时，获得的定标参数有限，无法准确判断定标参数的变化趋势。蒋兴伟等[9]对万山定标场附近海面高度进行了长期观测，结果显示：在距离万山定标场担杆岛10 km处的同时刻最大潮差为2 cm，在5 km范围内同时刻最大潮差小于1 cm。而在20 km范围内可能会产生最大5 cm的同时刻潮位差。因此，选择万山定标场验潮仪位置附近10 km上下范围内的HY-2B星下点进行定标可以尽可能地减小同时刻潮差所带来的影响。

影响验潮仪与星下点海面高度差异的因素主要为大地水准面、平均海面动力地形与海洋潮汐差异，大地水准面与平均海面动力地形之和为平均海平面。本文主要使用DTU10平均海平面模型对平均海平面高度进行校正，使用 TMD（Tide Mode Driver）潮汐模型对同时刻潮汐偏差进行校正。

3.2.1 DTU10 平均海平面校正

平均海平面（Mean Sea Surface，MSS）是在一个较长时期内剔除了周期性海面高度变化信息后的平均海面。平均海平面的全球分布与大地水准面分布基本一致，高度差为−2～2 m。平均海平面与大地水准面的不同之处在于，平均海平面除大地水准面外还包含了平均海面动力地形。平均海平面高度的表达式为

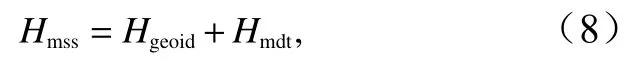
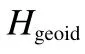
本文使用的平均海平面模型为丹麦国家空间中心发布的DTU10模型。相比于EGM2008大地水准面模型提供的最高1°分辨率，DTU10能够提供最高(1/60)°的远高于EGM2008的空间分辨率，覆盖范围为 90°S～90°N，其平均了包括 Jason-1/2、T/P、ERS、Envisat等多种高度计数据[10–11]。

不同于HY-2B使用的T/P参考椭球体，DTU10模型使用WGS84参考椭球体。WGS84与T/P存在约70 cm的高度差。T/P参考椭球体与WGS84参考椭球体的参数如表2所示。

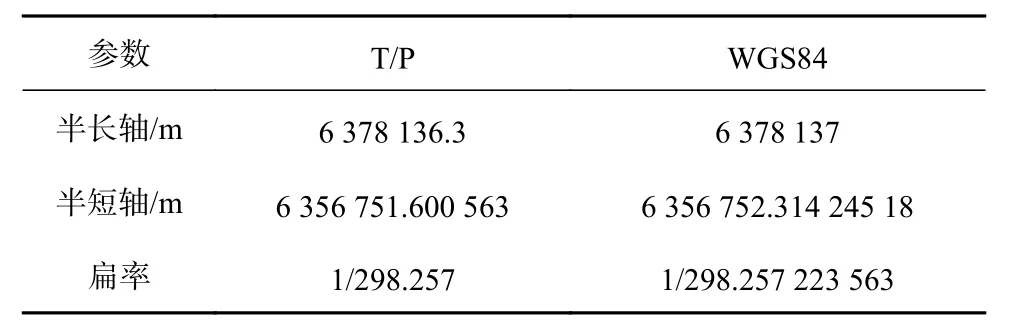
表2 参考椭球体参数Table 2 Reference ellipsoid parameters

在计算平均海平面高度时，需要进行严格的椭球转化，但是本文计算的是星下点与验潮仪处的平均海平面高度差，椭球差异可以忽略不计，因此不需要进行椭球转化。星下点与验潮仪距离与其对应的平均海面高度差如图2所示。

图2 平均海平面校正相关参数Fig.2 Parameters for mean sea surface correction

3.2.2 TMD 潮汐模型校正

TMD模型是一个基于最小二乘拟合的全球潮汐模型，同化了众多高度计产品数据。TMD模型提供的中国近海区域模型同化了531个周期的T/P高度计数据，225个周期的Jason-2数据，249个周期的Envisat浅水海面高度数据，共计156 779个星下点，其中代表性的站点有915个。此外，使用了总计104个验潮仪，其中包含51个沿岸验潮仪，44个TSW浅水验潮仪与9个TC沿岸验潮仪的长期观测数据进行误差校正。其中国近海区域模型为1 801×2 161的网格，分辨率能够达到（1/30）°，很好地满足了将沿岸验潮仪潮汐外推至星下点的需要[12]。

TMD 模型能够提供 8 个分潮 M2、S2、N2、K2、K1、O1、P1、Q1分别的相位、振幅、潮汐调和常数。在使用时可以根据需要选取不同的分潮进行调和分析。本论文在计算验潮仪与星下点潮差时选择了全部8个分潮进行潮汐预报。

根据TMD模型进行潮汐预报前首先验证TMD潮汐模型的准确性。使用TMD模型预报的验潮仪处海面高度与验潮仪实际测量结果对比结果如图3所示。

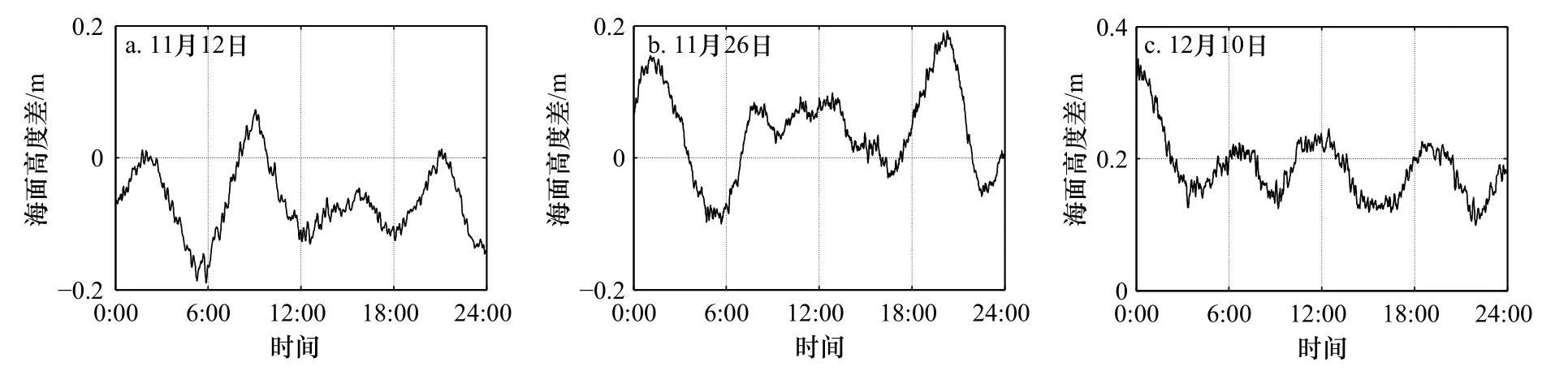
图3 TMD潮汐预报模型海面高度与验潮仪实测海面高度差Fig.3 Sea surface height differences between TMD tide prediction and tide gauge

潮汐模型的预报结果与实测结果存在着最大约0.35 m，均方根误差为0.18 m的差异。虽然潮汐模拟的潮位与实测潮位存在一定差距，但是二者表征的参数并不完全一致。潮汐模型反映的是潮位变化，验潮仪测量的是水位变化，水位数据需要采用调和函数提取水位数据中的潮汐部分再进行验证。

3.3 通过 HY-2B 高度计获取 SSHalt

本文通过HY-2B的IGDR产品计算验潮仪附近星下点海面高度。HY-2B的二级IGDR产品除了记录了星下点的经纬度与时间信息外，还提供了各种误差校正项，包括实时仪器误差、测距误差、地球物理误差等项。经过式（2）中去除误差校正项后，3次过境时分别测得的海面高度如图4所示。

图4 HY-2B 高度计测量沿轨星下点海面高度Fig.4 Sea surface height of calibration point from HY-2B altimeter

除周期003由于轨道漂移，星下点接近陆地，只获得1个测量值外，在周期001与周期002皆获得了1个以上的沿轨星下点海面高度，海面高度的测量值随着高度计升轨纬度的逐渐增加而逐渐降低。

3.4 定标结果

在经过上述误差校正后，可以通过式（5）计算得到HY-2B雷达高度计在发射后前3个周期的定标参数偏差，如图5所示。

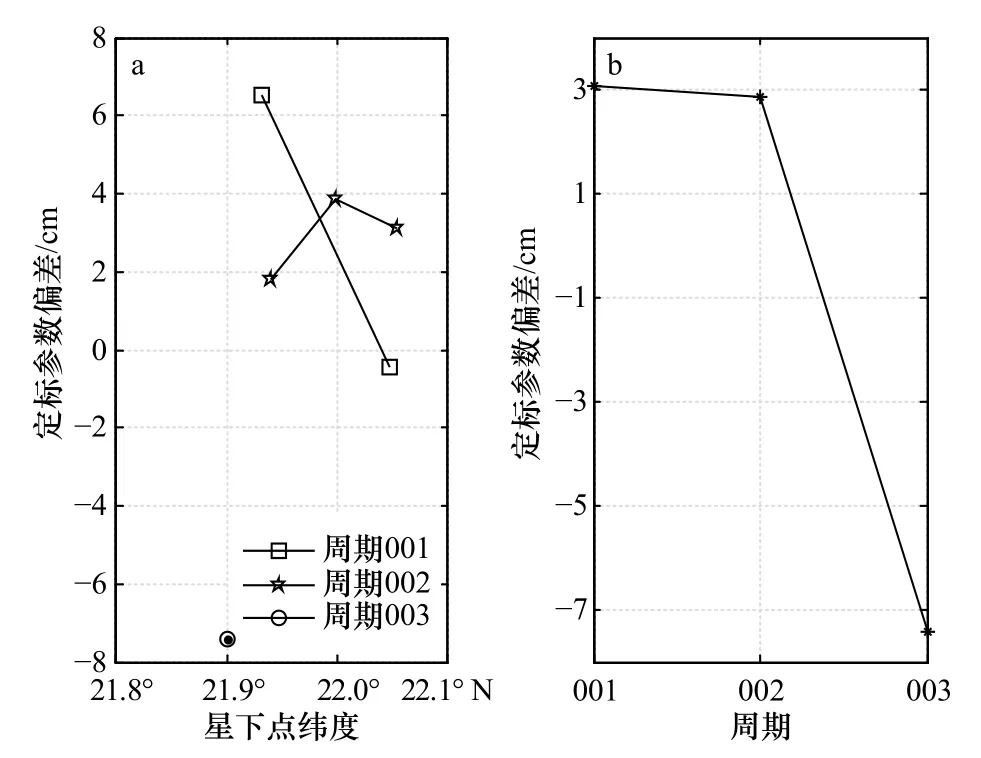
图5 HY-2B 前 3 个周期的定标参数偏差Fig.5 Calibration bias of HY-2B in first 3 cycles

计算得到3个周期的HY-2B雷达高度计定标参数分别为（3.06±3.48）cm、（2.85±1.03）cm、−7.41 cm，由此可见，高度计的定标参数存在沿星下点与轨道变化的差异。后续需要对HY-2B雷达高度计进行持续定标以确定漂移的大小以及原因。

4 结语

本文使用2018年11−12月于万山定标场布放的沿岸验潮仪对HY-2B雷达高度计进行了初步的定标工作，定标结果表明，HY-2B在珠海万山使用沿岸验潮仪定标可行且定标结果良好，定标参数总体比较稳定，存在少量漂移。

目前万山定标场的大地水准面已经测量完成，后续定标时将使用测量的大地水准面与平均动力地形代替本文中的DTU10平均海平面。万山定标场附近的浅水分潮模型没有建立，使用TMD模型进行潮汐外推时存在较大误差，无法精确地将沿岸验潮仪的测量结果外推至星下点。目前万山定标场已经建成永久性验潮站，后续将使用验潮仪数据建立更精确的潮汐模型。本文中验潮仪的布放时长仅有1个月，包含3个HY-2B重访周期的数据，测量数据较少。随着万山定标场的建设，GNSS浮标与永久性验潮站的布放与建立，多种现场观测的海面高度数据能够相互补充，未来HY-2系列高度计的定标精度能够不断提升。