沿岸流不稳定运动传播特性的小波相干谱分析

任春平，刘宇，赵喜萍

(1.太原理工大学 水利科学与工程学院，山西 太原 030024)

1 引言

沿岸流不稳定运动是指水平二维水流速度出现长周期波动，其波动周期一般大于100 s，属于超低频运动。这种长周期波动会伴随着沿岸流在沿岸方向传播，在传播过程中会诱导出大尺度涡旋，引起物质输移、能量交换，使得破波带内外水动力特性更加复杂，因此，其在时频域的传播特性对于岸滩演变、污染物、鱼卵等生物在垂直岸线和沿岸方向的输移、迁移有重要影响[1]。

目前，对沿岸流不稳定运动生成机理和数值研究已经取得了比较多的成果，但对于其传播特性还有待深入研究。Bowen和Holman[2]建立了沿岸流不稳定理论模型，Özkan-Haller和Kirby[3]基于二维浅水方程建立了沿岸流不稳定运动的数值模型，Dodd等[4]在Bowen和Holman的理论基础上建立了考虑底摩擦、侧混影响的不稳定模型。Reniers等[5]和Noyes等[6]分别在实验室内和现场观测到并利用频率波数谱分析了沿岸流不稳定运动，这些研究对推动沿岸流不稳定运动的研究起到了重要作用。要想用频率波数谱对沿岸流不稳定运动进行分析，需要在沿岸方向布设的流速仪多于2个，且频率波数谱主要用来从色散关系上证明沿岸流不稳定运动的存在，并不能像小波相干谱那样进行时间−空间域不稳定运动相关程度的分析。Ren等[7]基于线性不稳定理论，分析了平直斜坡上实验观测到的沿岸流不稳定运动。任春平等[8]对沿岸流不稳定运动和边缘波运动二者的相互关系做了实验研究，结果证明了沿岸流不稳定运动与边缘波不但可以共存（在垂直岸线方向和平行岸线方向），而且在沿岸方向能量有交换。沈良朵[9]研究了沿岸流非线性不稳定演化的特征。

上述研究集中在沿岸流不稳定运动产生机理及发展演化上，前提是不稳定运动在空间上同时产生，对于不稳定运动在空间产生的相位特性（即传播特性）没有涉及。本文即着眼于此，对沿岸流不稳定运动传播特性进行了分析。小波相干分析法可以分析该现象在空间的相关程度及相位差，通过该分析可以理解其传播特性以及入射波况对它的影响。由此得到的小波相干谱不仅可以用于确定两个时间序列在时频域的显著性关系，而且可以得到两个时间序列的相位差信息，这就为分析沿岸流不稳定运动传播特性提供了极大的便利。如果利用该方法能够计算得到平行于沿岸方向两个位置处沿岸方向流速时间历程的小波相干谱，就可以分析超低频区域内信号的相干特性，也就可以反映出沿岸流不稳定运动在沿岸方向的传播特性。Ruiz-Merchán等[10]和 Conde-Frias等[11]利用小波相干方法分析了重力波和低频波对波面升高、垂直岸线方向和沿岸方向速度的影响。

本文对所选实验波况，根据两列流速仪实测流速的时间历程，确定破波带内每列测量杆上沿岸流时均值最大的位置以及该位置向岸线和向海方向相邻两个位置，同时确定出另一列测量杆上的位置，对距离岸线相同位置处的沿岸方向流速时间历程做小波相干谱，以此分析沿岸流不稳定运动时频域传播特性及入射波况、地形对其传播特性影响。

2 实验简介

本文以大连理工大学海岸和近海工程国家重点实验室的沿岸流实验为基础，分析沿岸流不稳定运动在沿岸方向的传播特性。图1给出了实验布置，实验海岸地形为平直斜坡，其坡度分别采用1∶100和1∶40两种（图2），斜坡坡脚线与造波机夹角为30°，垂直岸线的两列流速仪共32个，每列16个，流速仪为双向流速仪，可以测量垂直岸线和沿岸方向的速度。从床底算起，流速仪布设于水深的1/3处，图3给出了1∶40地形上流速仪的放置位置，图4给出了波况4和波况9分别在x=2.5 m和x=4.0 m采集的沿岸方向流速时间历程。入射波分为规则波（波况1～5）和随机波（波况6～11），共11个波况，见表1，各组波要素造波时采用Jonswap谱，其谱峰升高因子为2.5。

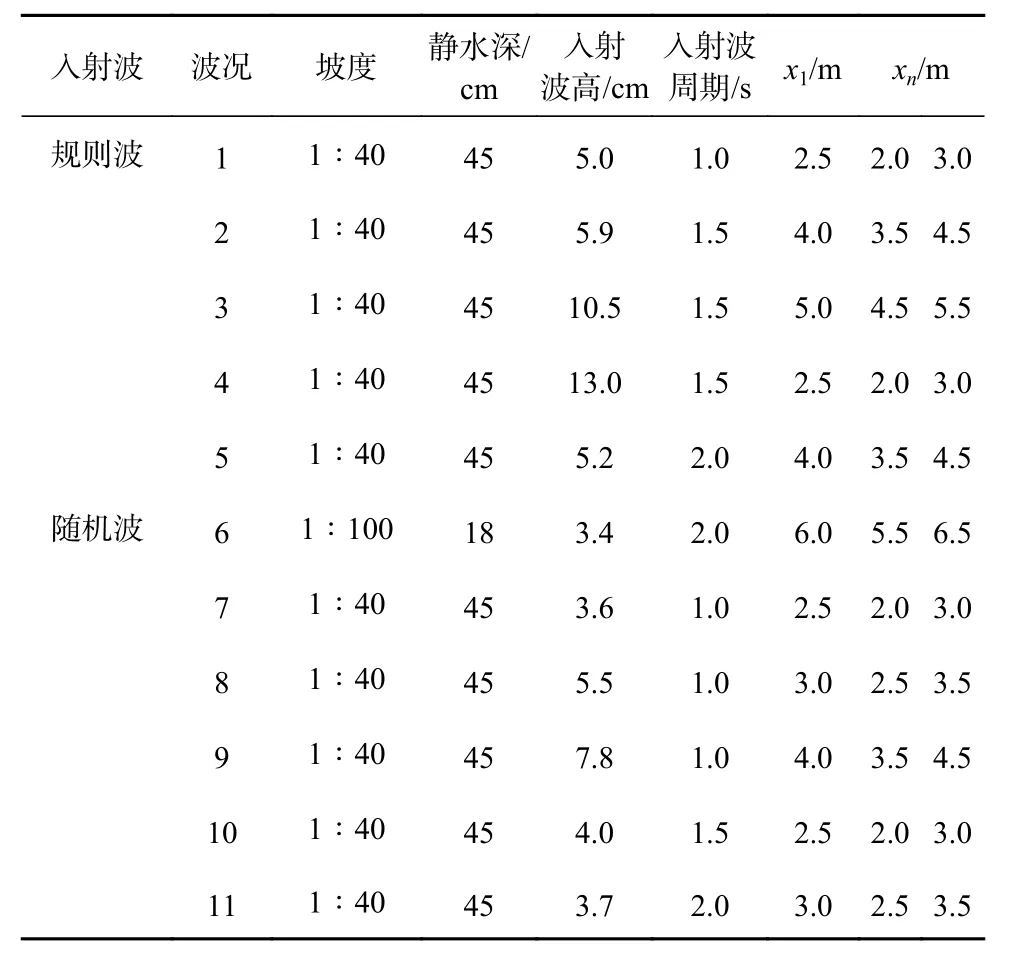
表1 波况参数Table 1 Wave parameters

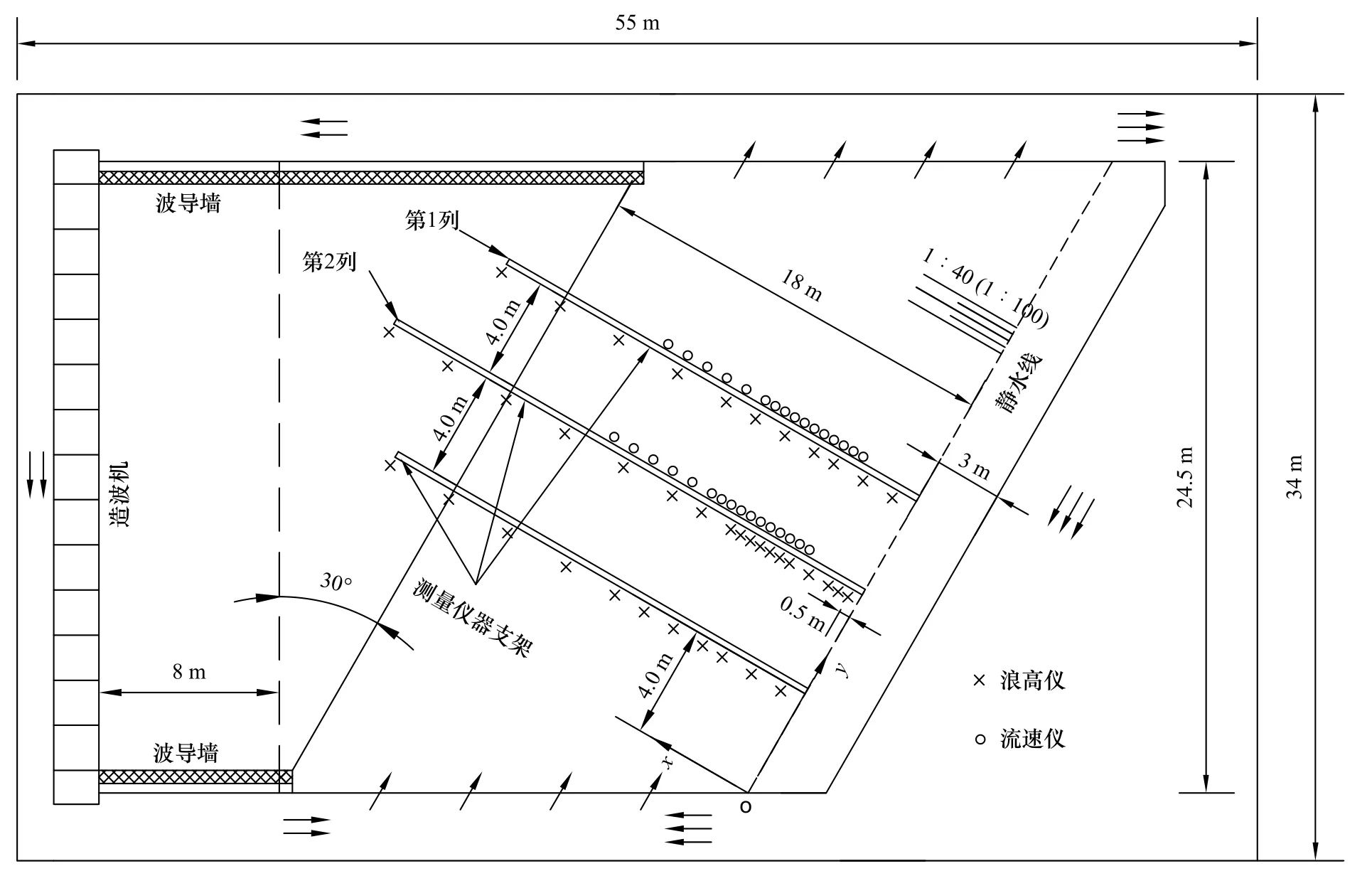
图1 实验布置Fig.1 Experimental layout

图2 实验地形Fig.2 Bottom profile

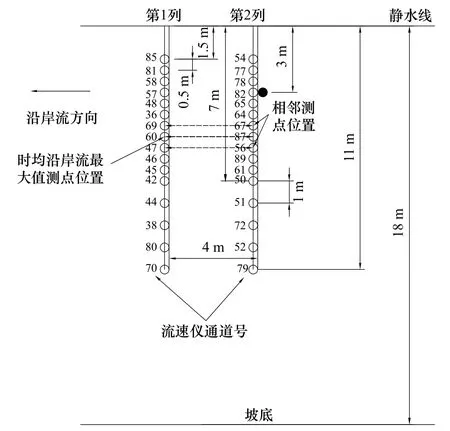
图3 1∶40 地形流速仪布置Fig.3 The layout of velocity meters for slope 1∶40

图4 波况 4 和波况 9 分别在 x=2.5 m 和 x=4.0 m 处采集的沿岸方向流速时间历程Fig.4 Time series of alongshore velocity at x=2.5 m and x=4.0 m for Case 4 and Case 9

3 小波相干分析方法

3.1 交叉小波变换

对于两个同步记录的随机时间序列xn、yn，对应的小波谱分别为WX、WY，为了研究它们之间的相关性，就需要进行交叉变换分析。小波交叉变换定义为WXY=WXWY∗，“*”表示复共轭，小波交叉谱 WXY为复数，所以，小波交叉谱能量定义为 |WXY|。实际上，小波交叉变换就是xn、yn协方差的时间尺度分解，它在时间轴上的积分即为小波交叉谱，其置信度水平源于两个 χ2分布小波谱乘积的平方根[12]。因此，小波交叉谱变换刻画了两个同步时间序列在时间−频率空间上的局部协方差，可以揭示它们共同的高能量区以及相位关系。

3.2 小波相位差

3.3 小波相干

所谓小波相干是指在时间−频率空间中两个同步时间序列共同变化区域（但不一定具有高能量）的相似程度。

小波交叉谱可以在时间−频率空间中刻画出时间序列里周期性强度一致的区域。但是在时间−频率域内局部化范围内，两种同步信号的相关程度反映不出来，这就需要小波相干的概念来描述。小波相干被用来度量时频空间中两个同步时间序列的局部相关程度，即使对应的是小波互谱中的低能量值区域，两者在小波相干谱中的相关性也可能很显著。

对于两个同步记录的随机时间序列xn、yn，其小波相干系数定义如下：

式中，s 为圆标准差；WnX、WnY、WnXY分别为时间序列xn、yn的小波变换和交叉小波变换；S为光滑算子，其定义如下：

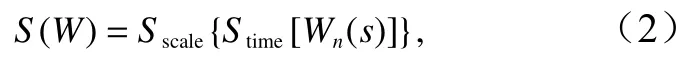
式中，Sscale表示沿着小波尺度轴进行光滑；Stime滑算子是很自然的，这样它就具有与所用小波相似的结果，其表达式如下：

式中，c1、c2为无因次常数，由具体时间序列的数值确定，Π为矩形函数，公式为

3.4 置信区间

由于小波不能够在时域完全局部化，所以小波变换的结果会受时间序列边缘的影响。因此引入锥形域分析考虑数据截断边界的影响，并且数据边缘不连续引起的小波功率下降到边缘值的e−2倍。

小波互谱的显著性检验，可以采用假设某一频率上WX、WY凝聚为0的F分布检验方法。本文按下式直接估计给定信度α条件下小波交叉谱的临界值置信区间的确定方法对于给定背景功率谱（pk）的平稳过程产生信号的零假设，可以评估小波功率的统计显著性[12]。

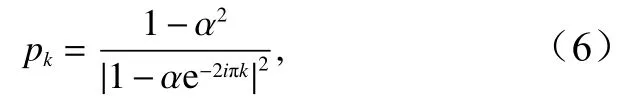
式中，k为傅里叶频率指数。

3.5 信号验证

为了清楚的理解小波变换、小波交叉谱及小波相干的性质，并验证程序的正确性，下面对测试信号进行小波交叉谱及小波相干的分析。考虑到沿岸流场中存在超低频和高频信号，因此选取的测试信号由低频和高频信号组成，两个测试信号分别为 X=y1+y2+y3，Y=y2，其中，

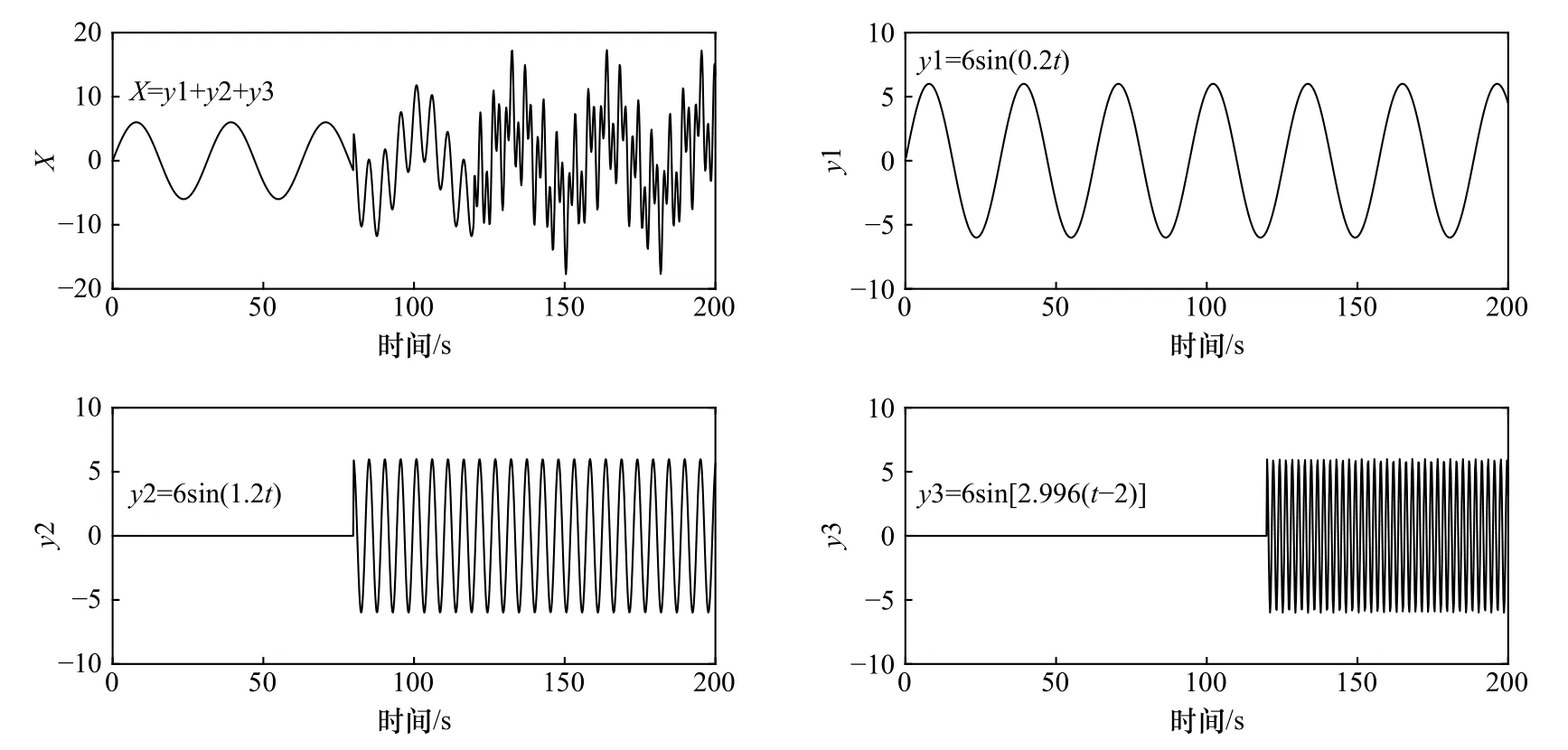
图5 X、y1、y2 及 y3 信号Fig.5 Test signals of X,y1,y2 and y3

图6分别给出了X和Y两个信号的小波谱及它们之间的小波交叉谱和小波相干图。由图6a可以看出组成X的3个信号y1、y2及y3在整个时间域上都能够识别出，y1在整个0～200 s都具有最强的能量，周期约 31.40 s。y2 和 y3 分别从 80 s和 120 s被识别出，周期分别约 5.23 s和 2.10 s。图 6c给出的是 X 和Y两个信号的小波交叉谱，小波交叉谱可以在时间−频率空间中刻画出时间序列里周期性强度一致的区域，从该图可以看出，X和Y两个信号在80～200 s之间，周期为5 s的能量存在很强的一致性，这与X和Y两个信号的特性是吻合的。图6d给出了X和Y 两个信号的小波相干谱，周期为 31.40 s、5.23 s、2.09 s 3种波动，它们满足倍频的关系，所以相关性比较明显。另外，可以看出在小波交叉谱中周期性能量一致的区域（80～200 s，周期为 5.23 s），这两个信号有很强的相似性，相关系数接近1，这样就可以识别出两个信号中具有相同频率成分的相干性，之所以在0～80 s之间也出现有相干系数接近于1的区域，是因为间隔以及数据截断的影响。

图6 X（a）和 Y=y2（b）的小波谱、X-Y 小波交叉谱（c）及 X-Y 小波相干谱（d）Fig.6 The wavelet power spectrum of X (a) and Y=y2 (b),and X-Y cross wavelet spectrum (c) and X-Y wavelet coherence spectrum (d)

在图6c和图6d中还给出了X和Y两个信号的相位差，如图中箭头所示。另外，图6每个图都给出了95%的置信区间，即图中圆锥形域内为95%置信水平。

4 规则波入射条件下沿岸流不稳定运动时频域特性

4.1 分析位置确定及数据预处理

根据沿岸流不稳定理论，其不稳定运动的产生是由沿岸流在垂直岸线方向存在速度剪切引起的，也将其称为剪切波。根据时均沿岸流速度剖面可以判断，速度梯度最大位置一般出现在时均沿岸流达到最大值的位置。因此，在第1根测量杆上确定时均沿岸流最大值位置及紧邻最大值的向岸线方向和向海方向的测点位置，对这3个位置与第2根测量杆上距离岸线相同位置处的沿岸方向流速时间历程，做小波相干谱，由于沿岸流不稳定运动在沿岸方向表现明显，所以只分析了沿岸方向速度的小波相干性。表1给出了波况1～11所确定小波相干分析位置，x1为时均沿岸流最大值位置，xn为与x1在向岸线和向海方向相邻测点对应的坐标。图3中标示了波况3根据实验结果确定的时均沿岸流最大值位置及向海和向岸线方向相邻位置。

在分析前对采集数据进行消除趋势项处理，且对沿岸流稳定出现后运动场进行分析，因此规则波和随机波情况分别对50 s和150 s后的时间历程作小波相干谱。

4.2 时频域传播特性及相位特性

图7至图11分别给出了波况1～5的3个位置处的小波相干谱，同时给出了相位差，如图中箭头所示。由图7可以看出，3个位置（2.5 m为时均沿岸流最大值出现的位置）得到的小波相干谱中，相干系数接近 1 的周期带大致有 3 个：0.25～0.5 s、1～4 s、16～32 s。0.25～0.5 s这个范围内 0.25 s、0.33 s以及 0.5 s与1 s入射波成倍频关系，所以这个范围相关性较强。1～4 s这个强相干信号是入射波所引起，说明破波带内波浪破碎后，其速度组成中有入射波浪引起的速度，表明破波带内的水动力要综合考虑波流作用。在16～32 s周期带内，也出现了强相干信息，特别是在2.5 m处，其强相干信号对应的周期甚至大于32 s，这说明出现了超低频信号，也就是沿岸流不稳定运动。通过与2 m和3 m处小波相干谱比较发现，对于大于32 s的超低频信号，在2 m和3 m处相干性减弱，说明在距离岸线2 m和3 m处沿岸流不稳定运动减弱，其传播特性也表现的比较弱。沿岸流不稳定运动是由垂直岸线方向沿岸流存在速度梯度引起的，2.5 m处其速度梯度接近最大，引起诱导出较强的不稳定运动，而随着沿岸流速度梯度向岸线和向海方向的减弱，其不稳定运动也减弱，因此该结果与沿岸流不稳定运动的剪切产生机理相吻合。在2 m及3 m的小波相干谱中出现了周期约为16 s的强相干信号，这是由于边缘波[13]的产生所引起的，而在2.5 m处则没有出现，说明在沿岸流不稳定出现后，会抑制边缘波。在某些位置的相关性不够强，还可能与边缘波的空间分布有关，在垂直于岸线方向，有的地方流速较大，有的地方流速较小。

图7 波况 1 中距离岸线 2 m（a）、2.5 m（b）及 3 m（c）处对应的小波相干谱Fig.7 Wavelet coherent spectrum at x=2.0 m (a),x=2.5 m (b) and x=3.0 m (c) under Case 1

由图7b可以看出在，2.5 m处出现的周期大于32 s的低频运动，其相干系数约为0.60，在2 m和3 m处则没有出现，说明该波况下沿岸流不稳定运动可能比较弱，也可能是采集时间历程较短(数据处理后，采集时间约为 130 s)，Reniers和 Battjes[14]也指出在他们的实验中，规则波情况下没有观测到沿岸流不稳定运动。

从图8至图11可以看出，在这几个波况下，3个位置处大于32 s周期的信号其相干性都较弱，只有在波况2下，4.5 m处（图8c）出现了相干系数接近1的超低频信号。由此可以看出，在本文实验规则波入射情况下，沿岸流不稳定运动较弱。

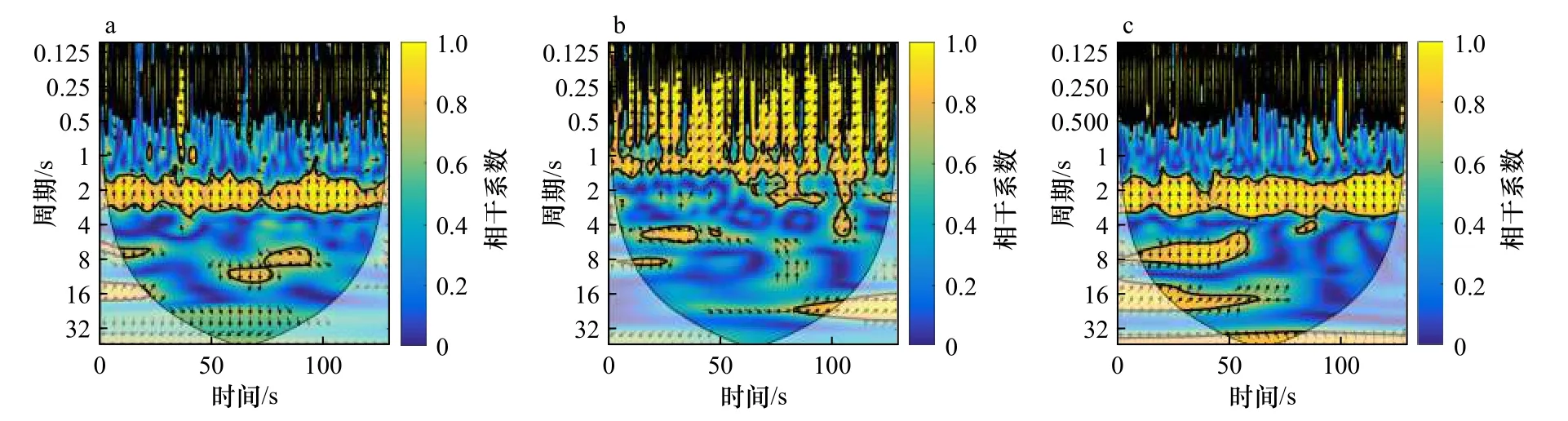
图8 波况 2 中距离岸线 3.5 m（a）、4.0 m（b）及 4.5 m（c）处对应的小波相干谱Fig.8 Wavelet coherent spectrum at x=3.5 m (a),x=4.0 m (b) and x=4.5 m (c) under Case 2

4.3 入射波高、周期对沿岸流不稳定运动传播特性的影响

从波况1～3可以看出，入射波周期不变，其对应的波高由5 cm增加到12.6 cm，从图7至图9可以看出，随着入射波高的增加，波况2在x=4.5 m处（图8c）出现了周期约为64 s的相干性很强的沿岸流不稳定运动，波况3在x=5.0 m处（图9b）也出现了周期约为64 s的沿岸流不稳定运动，表明随着入射波高的增加，沿岸流垂直岸线方向的速度梯度增加，同时非线性也随之增强，导致更容易诱导出沿岸流不稳定运动。

图9 波况 3 中距离岸线 4.5 m（a）、5.0 m（b）及 5.5 m（c）处对应的小波相干谱Fig.9 Wavelet coherent spectrum at x=4.5 m (a),x=5.0 m (b) and x=5.5 m (c) under Case 3

波况1与波况4，波况2与波况5这两对波况入射波高相近，入射波周期相差0.5 s。通过分析波况4（图 10）、波况 5（图 11）这两种情况下，3 个位置呈现出的沿岸流不稳定运动特性与波况6和波况2相似，分别比较波况1和波况4，波况2与波况5的小波相干谱，发现入射波周期对沿岸流不稳定运动的传播特性影响较小。

图10 波况 4 中距离岸线 2.0 m（a）、2.5 m（b）及 3.0 m（c）处对应的小波相干谱Fig.10 Wavelet coherent spectrum at x=2.0 m (a),x=2.5 m (b) and x=3.0 m (c) under Case 4

图11 波况 5 中距离岸线 3.5 m（a）、4.0 m（b）及 4.5 m（c）处对应的小波相干谱Fig.11 Wavelet coherent spectrum at x=3.5 m (a),x=4.0 m (b) and x=4.5 m (c) under Case 5

5 不规则波入射条件下沿岸流不稳定运动时频域特性

5.1 时频域传播特性及相位特性

与规则波情况类似，不规则波入射情况下确定的分析位置见表1。图12至图17分别给出了波况6～11 的3个位置处的小波相干谱，同时给出了沿岸方向流速时间历程的相位差，如图中箭头所示。

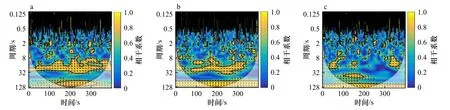
图12 波况 6 中距离岸线 5.5 m（a）、6.0 m（b）及 6.5 m（c）处对应的小波相干谱Fig.12 Wavelet coherent spectrum at x=5.5 m (a),x=6.0 m (b) and x=6.5 m (c) under Case 6

由图12可以看出，3个位置（6.0 m为时均沿岸流最大值出现的位置）得到的小波相干谱中，相干系数接 近 1 的 周 期 带 大 致 有 3 个 ：0.25～2 s，16～32 s，64～128 s。该波况入射波周期为 2 s，0.25～2 s这个范围内 0.25 s、0.5 s、1 s、2 s都是与入射波周期呈倍频关系，所以相关性较强。与规则波入射情况相似，说明破波带内波浪破碎后，其流场速度组成中有入射波浪引起的速度。在16～32 s周期带内，也出现了强相干信息，特别是在5.5 m和6.0 m处，其强相干信号连续出现，说明出现了超低频信号，根据低频波周期推测，这可能是由边缘波引起的，说明在试验中靠近岸线处出现了边缘波。并且16～32 s强相干信号在6.5 m处变弱，说明随着距离岸线的增加该周期信号减弱，这也从另一方面说明，在靠近岸线处出现了边缘波，同时该16～32 s周期信号基本呈现出同相特性，说明边缘波基本是同时产生的。

对于周期为64～128 s的信号，在3个位置处其相干系数接近1，说明在3个位置处都有沿岸流不稳定运动出现，并且在5.5 m和6.0 m处的相位差都约为 90°，而在 6.5 m 处则约为−30°。

从图13至图17可以看出，在这几个波况下，3个位置处64～128 s周期的信号其相干性都较强，只有波况 7（图 13）在 2.0 m 和 2.5 m 处该信号的相干系数较低（约为0.6）。并且从图14至图17可以看出，这4个波况，每个波况下3个位置处64～128 s信号的相位差都一致，波况8、9、10、11对应的相位差分别约为−30°、−30°、30°、30°。并且波况 6 和波况 7 分别在6.5 m 和 3.0 m 处得到的相位差也约为−30°。之所以产生正、负相位差，可能是由于在不规则波情况下破波点有变化[15]，导致不稳定运动在两个断面上产生正或负相位，其相位差都约为30°，这与实验入射角（实验波况的入射角都为30°）相近，或者称为相位守恒，这需要进一步进行理论分析。

图13 波况 7 中距离岸线 2.0 m（a）、2.5 m（b）及 3.0 m（b）处对应的小波相干谱Fig.13 Wavelet coherent spectrum at x=2.0 m (a),x=2.5 m (b) and x=3.0 m (c) under Case 7

图14 波况 8 中距离岸线 2.5 m（a）、3.0 m（b）及 3.5 m（c）处对应的小波相干谱Fig.14 Wavelet coherent spectrum at x=2.5 m (a),x=3.0 m (b) and x=3.5 m (c) under Case 8

5.2 入射波高、周期对沿岸流不稳定运动传播特性的影响

波况7～9，入射波周期不变，其对应的波高由3.6 cm增加到7.8 cm，从图13至图15可以看出，波况7在3.0 m处强相干的超低频信号周期处于100～110 s范围，而波况8和9则在64～128 s范围，说明随着入射波高的增加，生成的沿岸流不稳定运动周期范围将更广，同时非线性也随之增强，导致更容易诱导出沿岸流不稳定运动。

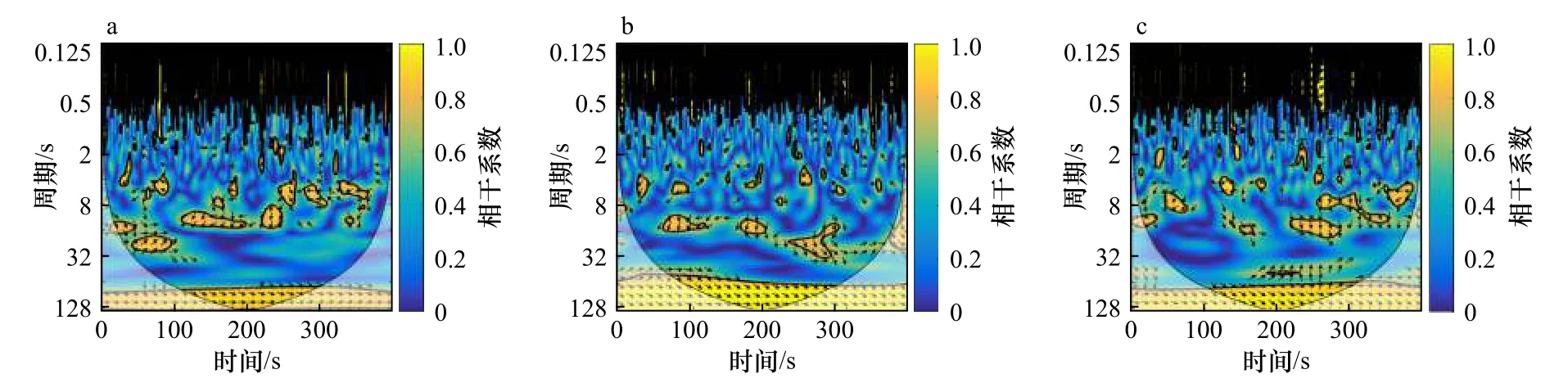
图15 波况 9 中距离岸线 3.5 m（a）、4.0 m（b）及 4.5 m（c）处对应的小波相干谱Fig.15 Wavelet coherent spectrum at x=3.5 m (a),x=4.0 m (b) and x=4.5 m (c) under Case 9

波况 7（图 13）、波况 10（图 16）以及波况 11（图 17），这3个波况入射波高相近，入射波周期分别为1.0 s、1.5 s及2.0 s。通过分析发现，入射波周期对沿岸流不稳定运动的特性影响较小，但是对于边缘波（周期约25 s）有较明显的影响，例如，波况 10、11 在 16～32 s范围内出现了强相干信号，而波况7中该信号的相干性显得有些弱，说明入射波周期对边缘波有较明显的影响。

图16 波况 10 中距离岸线 2.0 m（a）、2.5 m（b）及 3.0 m（c）处对应的小波相干谱Fig.16 Wavelet coherent spectrum at x=2.0 m (a),x=2.5 m (b) and x=3.0 m (c)under Case 10

图17 波况 11 中距离岸线 2.5 m（a）、3.0 m（b）及 3.5 m（c）处对应的小波相干谱Fig.17 Wavelet coherent spectrum at x=2.5 m (a),x=3.0 m (b) and x=3.5 m (c) under Case 11

5.3 坡度对沿岸流不稳定运动传播特性的影响

波况 6（入射波周期为 2.0 s，入射波高为 3.4 cm）和波况 11（入射波周期为 2.0 s，入射波高为 3.7 cm）入射波高与周期相近，只是坡度不同，分别为1∶100和1∶40，这两个波况下的小波相干谱，见图12和图17。本节将通过分析这两个波况的小波相干谱，研究坡度对沿岸流不稳定运动传播特性的影响。

通过比较图12和图17，可以看出波况6与波况11在3个位置处沿岸流不稳定运动都有较强相干性，前者不稳定周期范围约为 64～128 s，后者约为 100 s，说明1∶100坡上不稳定运动受浅化影响较明显，导致不稳定周期变化范围增大。就相位差而言，前者在 3 个 位 置 处分 别 为 90°、90°、−30°，后 者 为 90°、30°、30°，说明1∶100坡上不稳定运动相位差在垂直岸线方向有较大变化，而1∶40坡上则变化相对较小，这从另一方面说明1∶40坡上不稳定运动能量更强，或者说坡度越陡更易产生不稳定运动，这也与不稳定运动产生机理吻合，因为在陡坡情况下沿岸流垂直岸线方向速度梯度变化更大，也更易诱导出不稳定运动。

就16～32 s范围的边缘波而言，1∶100坡上的强相干域更加连续，说明在1∶100坡上更易诱导出边缘波，且其相位差在3个位置处基本接近。

因此可见，坡度越陡，越易诱导出超低频的不稳定运动，也就是其传播特性增强，坡度较缓的情况下，不稳定运动周期变化范围变大。另一方面，坡度越缓，边缘波传播特性表现的越明显。

6 结论

本文对所选实验波况，根据实测流速时间历程，确定破波带内沿岸流时均值最大位置以及该位置向岸线和向海方向相邻两个位置，对应的确定出另一列测量杆上相同位置，然后做小波相干谱。通过分析表明：

（1）不规则波更易诱导出沿岸流不稳定运动；沿岸流不稳定出现后，会抑制边缘波；破波带内波浪破碎后，其流场速度组成中有入射波浪引起的速度，表明破波带内的水动力要综合考虑波流作用。

（2）不规则波情况下破波点有变化，导致不稳定运动在两个断面上产生正或负相位，其相位差都约为30°，这与波浪入射角相近。

（3）入射波高的增加，非线性随之增强，生成的沿岸流不稳定运动周期范围将更广，沿岸流垂直岸线方向的速度梯度增加，导致更容易诱导出沿岸流不稳定运动；入射波周期对沿岸流不稳定运动的传播特性影响较小。

（4）坡度越陡越易诱导出超低频的不稳定运动，也就是在其传播特性增强，坡度较缓的情况下，不稳定运动周期变化范围变大。另一方面，坡度越缓，边缘波传播特性表现的越明显。