地震作用下渡槽内水体响应三维数值模拟与分析

杨梦薇，管光华

地震作用下渡槽内水体响应三维数值模拟与分析

杨梦薇，管光华*

（武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

【】研究输水渡槽在地震荷载作用下的水体响应特性，为渡槽振动条件下的流固耦合分析及满溢风险评估提供指导。采用FLOW-3D三维仿真软件，从地震荷载作用方式、地震荷载频率、渡槽内水体流量大小3个角度出发，设置了3组数值仿真实验，并由仿真结果分析了渡槽水体在典型地震荷载作用下的响应特性。渡槽边壁在靠近自由液面处受到水体的垂直作用力最大，其数值为底部和中部的10倍以上；施加单一方向地震荷载时，水平方向地震荷载水体波动比竖直方向大2.5%；地震荷载频率增大，水体运动剧烈程度先增大后减小，在一定区间内存在使得水体响应最为剧烈的频率；流量增大，水体对边壁的垂直作用力最大值被削弱20%以上，但水体漫顶的风险也随之增加。在渡槽结构进行抗震设计时应考虑自由液面附近的渡槽边壁强度。此外增大渡槽流量会减小水体对边壁的作用力，但渡槽漫顶风险也随之增加。

渡槽；地震响应；数值模拟；水位；垂直边壁加速度

0 引言

【研究意义】渡槽是输配水渠道系统中一种常见的交叉建筑物，常用于输送渠水跨越山冲、谷口、河流、渠道及交通道路等。渡槽作为交叉建筑物，除输水外还兼顾排洪、排沙、通航、导流多项功用[1]。作为水利工程中重要的输水建筑物，渡槽的结构安全与输水工程的稳定运行息息相关。影响渡槽运行安全性的非常规因素有地震荷载、温度应力[2-3]等。而随着我国引调水工程逐步向中西部地区推进，渡槽的抗震分析愈发引起人们的重视。譬如近年建设中的滇中引水工程，部分渡槽穿越强地震区，一旦渡槽在地震作用下发生破坏，将会导致全线供水中断，同时事故对工程所在地造成的破坏亦较为强烈[4]，则探索渡槽在地震荷载作用下的响应规律，并进行相应的抗震设计显得尤为重要。而关于结构的抗震分析，其主要的研究方法为时程分析法，但该方法仅针对结构本身而言[5]。对于渡槽这一特殊水工建筑物，在地震荷载作用下，如果仅仅考虑其结构自身的振动，而忽略了巨大的水体质量惯性作用，则结果与实际情况可能大相径庭[6-7]。因此分析地震作用下的渡槽结构安全，需要对槽内水体动边界特性有深入的认知。

【研究进展】地震发生时，渡槽在地震作用下发生振动，并给渡槽内的水以一定的作用力使之紊动，紊动的水体反过来又对渡槽的振动产生影响，这样的相互作用过程称为渡槽与水体的耦合作用[8]。此前，关于渡槽结构分析的方法主要有以下几种。首先是Westergaard的附加质量模型[9]，高兑现等[10]将其用至渡槽结构，将槽内的水作为附加质量进行计算，但该方法忽略了水的压缩性和紊动作用，只适用于渡槽结构动力学定性分析。之后Housner提出模拟脉动压力和对流压力的等效质量-弹簧模型[11]，季日臣等[12]、张多新等[13]以此为基础建立了渡槽FSI（Fluid Solid Interaction）动力学模型，但该方法仅适用于刚性槽墩的近似分析，对于柔性槽墩其计算结果偏危险[14]。希尔伯特-黄变换（Hilbert-Huang transform，HHT）是Norden等[15]在1998年提出的一种分析非线性非平稳信号的自适应时频处理新方法，张建伟将其用于提取渡槽结构振动的有效信息[16]，并用其对比FSI系统耦合模型和附加质量模型的计算结果，发现前者在模拟阶次和精度上均优于后者[17]。Hirt等[18]创立了ALE（Abitrary Lagrange-Euler）法，吴轶等[19-20]用该方法建立了U形、矩形渡槽水体大幅紊动的ALE模型，该方法可以有效模拟流体与结构的耦合作用，但建模及运算都较复杂。此外，关于渡槽结构分析的方法还有位移有限元模型[21]、位移-压力有限元格式[22]、边界元模型[23]，上述3种方法均未模拟真实流体，而用简化计算加以代替[24-25]。【切入点】综上所述，目前采用的渡槽结构分析方法均未将渡槽内流体作为研究对象单独分析而得出渡槽内的流体动态边界变化规律。【拟解决的关键问题】以位于某新建灌区的渡槽为工程背景，选取渡槽内水体的水位及垂直边壁加速度为分析指标，对不同地震荷载作用类型、不同地震荷载频率及不同流量工况下的水体进行数值模拟，研究地震作用下渡槽内水体的三维水流特性，为渡槽振动条件下的流固耦合分析及结构破坏机理与特点提供参考，亦可为渡槽的满溢风险评估提供指导。

(3)专业注重实验和实训课程，每学期开设3-4周课时集中实训，还将部分课程以“理论+实验”的方式教学，培育学生实务以及应用技术的能力。

1 材料与方法

1.1 研究物理模型

选用某新建灌区渡槽，采用CAD软件对渡槽上部结构及槽内水体进行建模，取渡槽的纵向计算长度为100 m，纵坡=1/1 000，糙率为=0.015。槽内初始水深为设计流量设=11.5 m3/s对应的恒定均匀流水深恒定=1.994 m[26]。渡槽的加大流量为加大=13.8 m3/s。图1为渡槽横截面示意图。

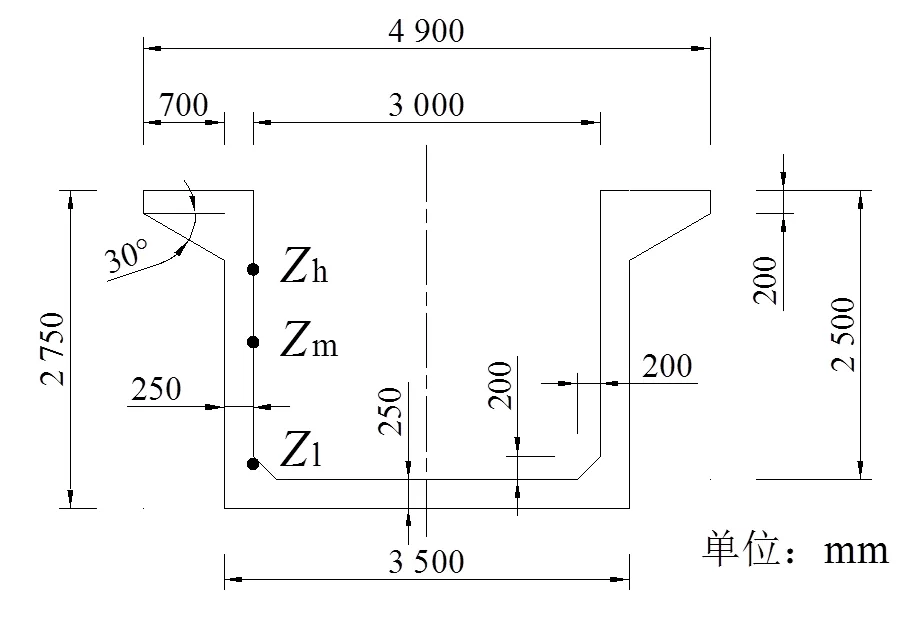
图1 渡槽横截面

1.2 参数设置及网格剖分

渡槽与流体接触的所有壁面均采用无滑移固壁条件，并选择计算精度和可信度较高的RNG（Renormalized group）-紊流模型进行仿真计算。对网格的6个面进行边界条件设定：渡槽入口处（max）设为流量进口边界，并设置进口流量；出口处（min）设为固定水位的压力出流边界，设压力为0，但给定下游水位为恒定=1.994 m，即为设计流量下对应的恒定均匀流水深；min、max以及min边界都是水流与渡槽的接触面，故设边界为墙边界；max设定为压力边界，并令压力及流体体积分数均为0[27-28]。

我国的外语导游主要为入境的外国友人方便在中国的游览而提供服务，其主要工作内容为来华的外国游客提供语言服务和旅游向导，解决游客在行程中的食、宿、行、游、购、娱等方面的各种问题。中国已连续多年保持全球第四大入境旅游接待国地位，在入境市场的供应链中，导游人员在其中发挥着不可或缺的重要作用。然而，与日益增长的入境游客数量不相符的情况却是我国的外语导游总量并不充足，存在需求大、缺口多的问题，在一定程度上影响了我国旅游产业的新兴客源市场的开拓。

选用不同尺寸的均匀网格作网格无关性分析，计算施加水平竖直地震荷载时，采用不同网格尺寸计算得到的渡槽左右边壁最高水位，以及渡槽左边壁代表位置处-方向垂直边壁加速度最值分别如表1和表2所示，表中的误差均为相对于最精细网格的计算结果。

由表1可知，网格尺寸由0.1 m减小至0.08 m、再减小至0.05 m时，计算出的左右边壁最高水位差异较小，较粗的网格相对于最精细网格的计算误差均小于0.3%。则加密网格对于水位计算结果影响较微弱。由表2可知，随着网格的加密，代表位置的加速度最值计算结果差异显著。其中0.1 m网格与0.05 m网格计算结果差异较大，其误差百分比均超过70%。而0.08 m网格相比0.05 m网格，计算结果误差均小于40%。考虑到加密网格带来的巨大计算时间成本，最终决定选用计算误差较小的尺寸为0.08 m的网格进行仿真计算。本研究数值模拟区域为计算长度100 m的渡槽及槽内水体，选用单元尺寸为0.08 m的单层网格，网格单元总数达1 742 500个。

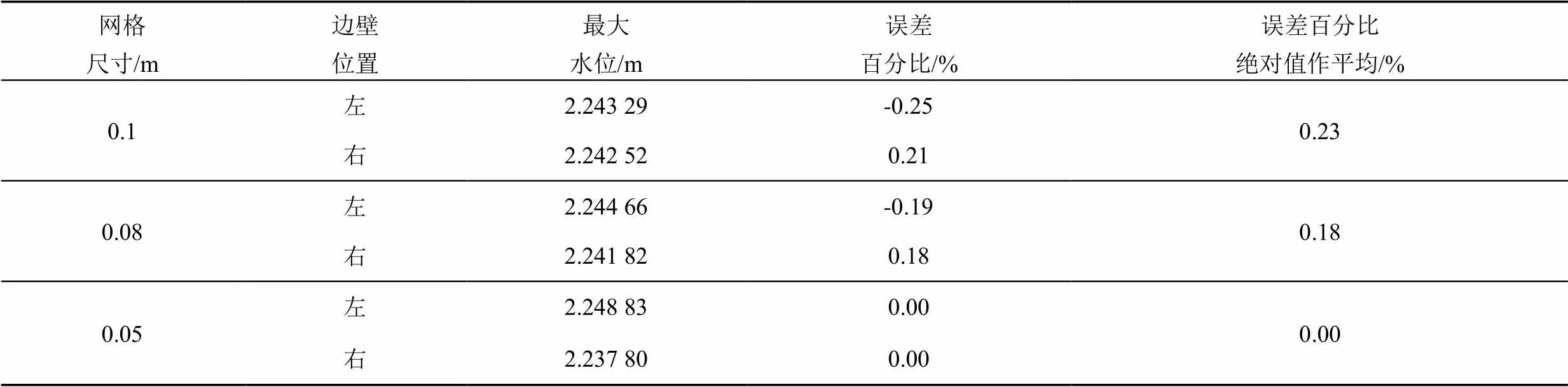
表1 不同网格划分计算的最高水位

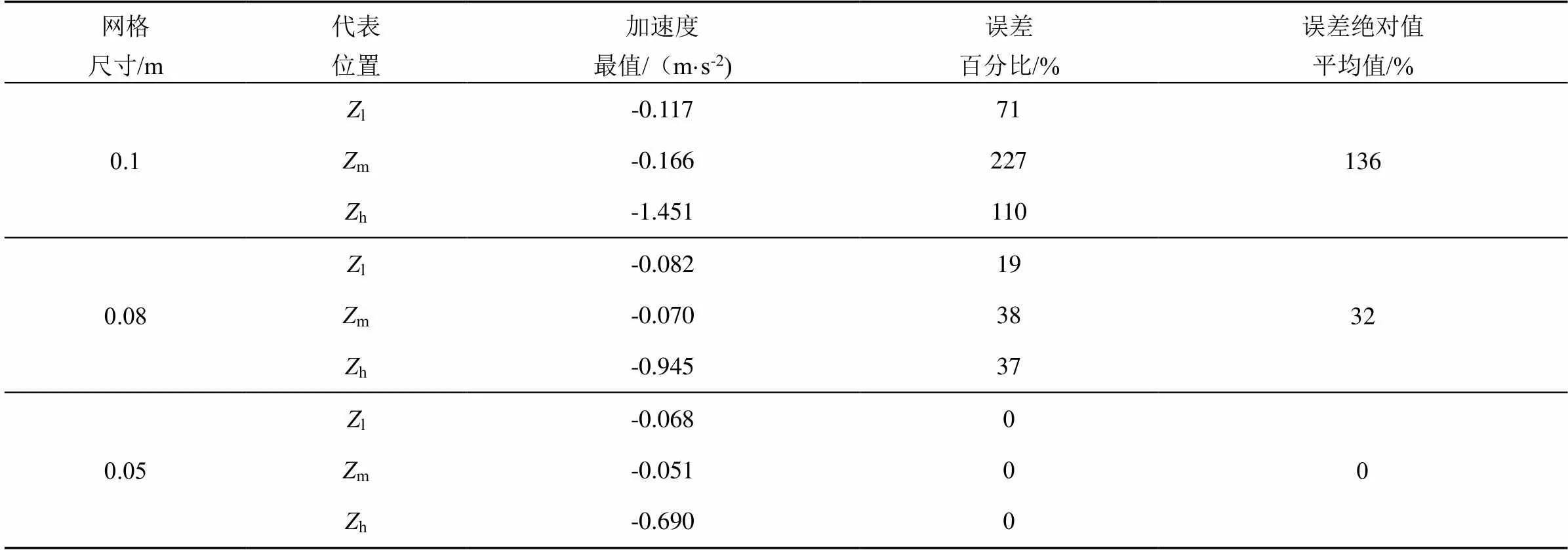
表2 不同网格划分计算的-x方向垂直边壁加速度最值

1.3 工况设置与地震波处理

考虑到垂直渡槽边壁的加速度是导致渡槽侧壁产生应变的主要原因，对渡槽中间截面（中=50 m）左边壁（左=0.244 m）处选取3个代表位置l=0.386 m、m=1.428 m以及h=2.069 m，分析由垂直边壁速度v计算得到的相邻时间点内的垂直边壁平均加速度。其中分析垂直边壁加速度的代表点位置如图1（a）所示。

此外，考虑到渡槽的安全性，选取渡槽在设计流量下受到水平竖直地震荷载时水体对渡槽左边壁有最大垂直边壁作用力的时刻作抗倾覆分析。经计算，得到抗倾覆力矩为倾覆力矩的96倍，远大于倾覆力矩，则渡槽虽然受到水体和惯性力作用，其结构仍安全，此时产生的倾覆力矩可以忽略不计。

论文还对KOYNA地震波进行了地震频谱分析，将缩放后的方向地震加速度在Matlab中作快速傅里叶变换（FFT变换），将原始波形转化为频谱输出，然后再选取典型频率，通过反傅里叶变换（IFFT）得到变换后的对应该频率的地震加速度[31]。由Matlab输出的频谱变换过程图如图3所示。又根据奈奎斯特采样定律，在信号转换过程中，为了完整保留原始信号的信息，采样频率应大于信号中最高频率的2倍。而实际应用中，采样频率一般为信号最高频率的2.56～4倍[32]。为避免地震波失真，最大采样频率取原地震加速度采样频率的4倍，即对频率=0～12.5 Hz范围内对应的地震加速度进行分析，并以=1.49、4.20、5.78、9.70 Hz的4组频率对应的地震加速度为典型进行分析。

笼统的说《摩西五经》是宗教书籍是不行的，要细读文本。必须感谢的是，冯象翻译中的解释和他附加的小标题，使《摩西五经》不再是信徒念的经，而是人文学者研究的文本。

基于AutoCAD进行二次开发的结构施工图审核软件对于连续梁的识别是根据连接柱的平面位置来确定的，而基于BIM技术的结构施工图审核技术是通过结构模型中的梁构件属性直接指定2根相同属性的梁构件属于1根连续梁，大大加快了读取构件的速度。

数据层采用PostgreSQL数据库，负责空间数据和属性数据的存取，维护各种数据间的关系，通过用户的调用完成对数据的持久化工作，并且保障整个系统数据源的安全性。另外，数据层还包括数据实体类与通用类库，二者均面向全局，前者主要定义了基础数据实体模型，便于规范业务数据实体对象。后者主要是封装程序开发经常用到的方法和操作，例如数据转换、字符串处理等。

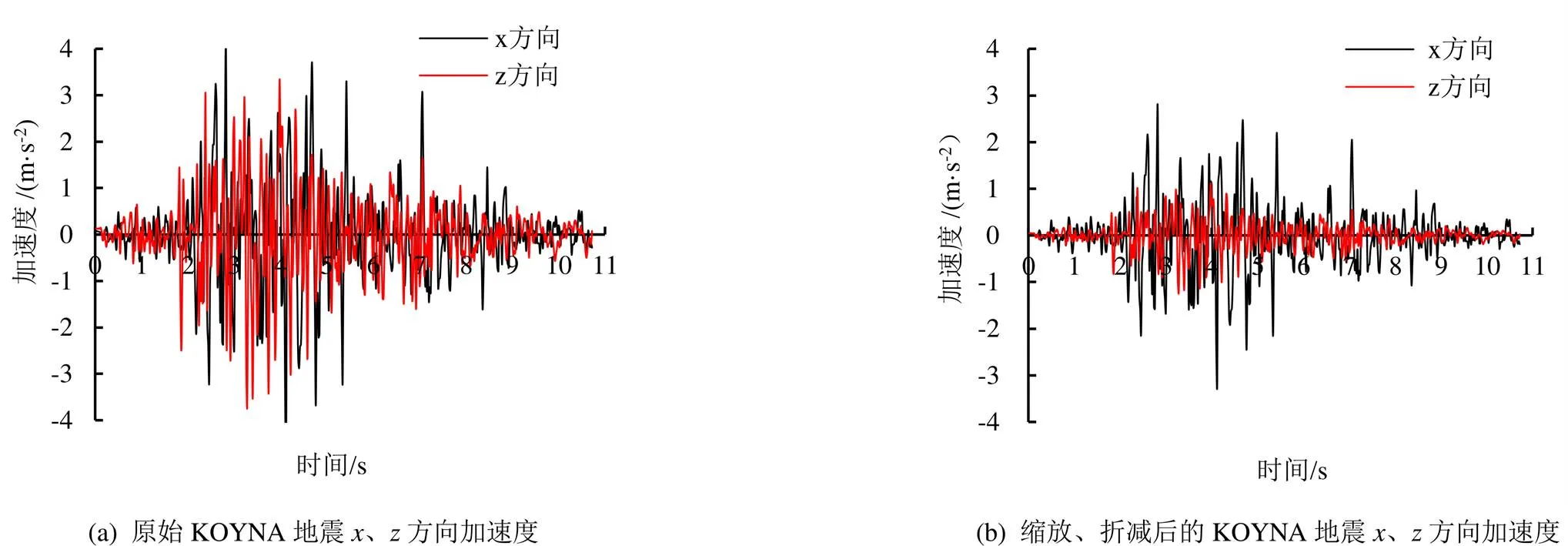
图2 KOYNA地震x、z方向加速度

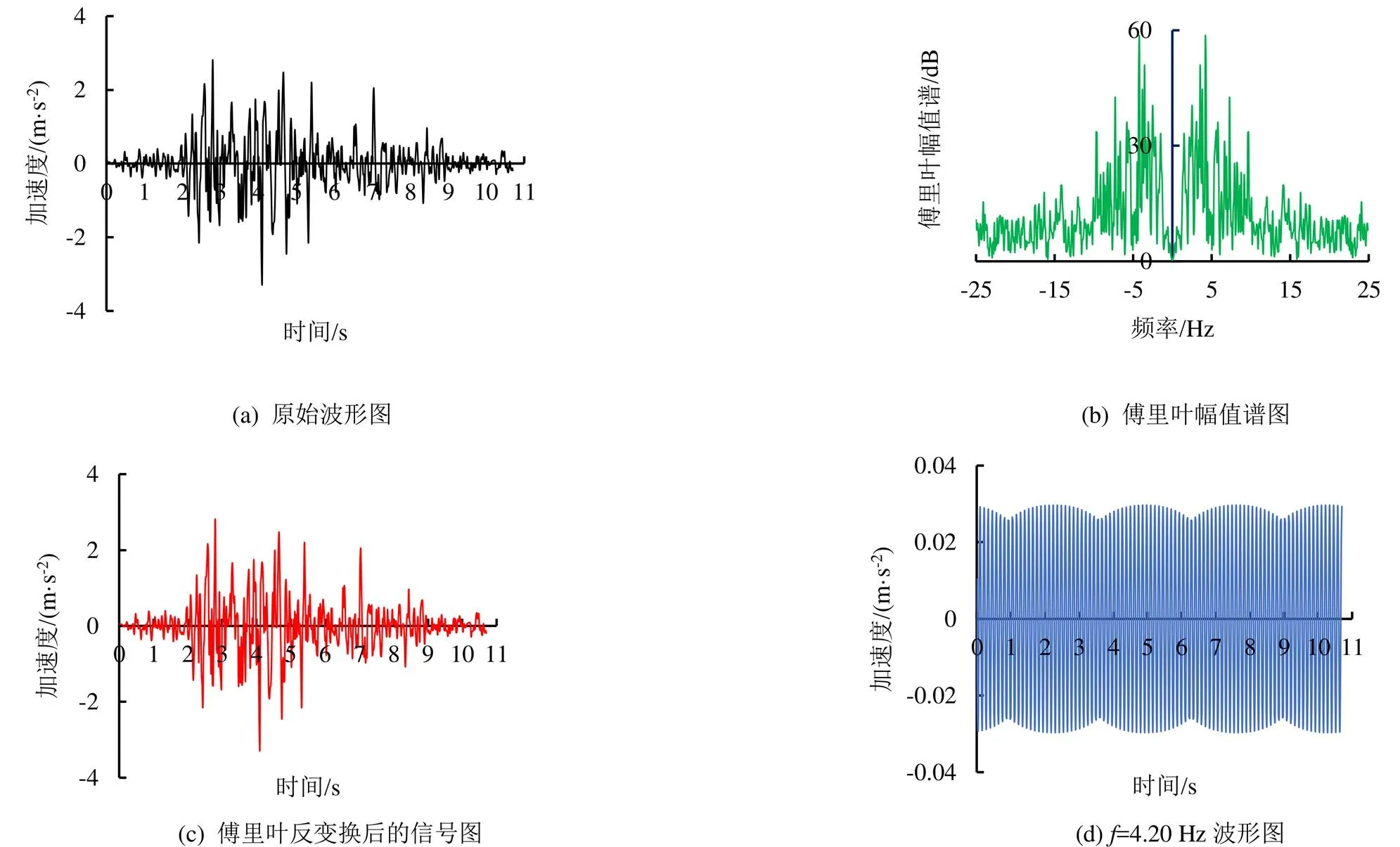
图3 Matlab输出的地震频谱分析过程

1.4 模型计算原理

模型计算时采用了离散的N-S方程格式以及紊流模型，其计算原理如下。

地震发生时，渡槽内的水流流动状态属于湍流，而N-S方程（Navier-Stokes方程）是描述黏性不可压缩流体动量守恒的运动方程，可以很好地求解湍流。FLOW-3D将N-S方程进行雷诺平均化，求解的是时均化的N-S方程[33-34]。

按照《固体废物浸出毒性浸出方法醋酸缓冲溶液法》(HJ/T 300—2007)对飞灰样品进行毒性浸出。吸取17.25 mL冰醋酸至1 L容量瓶，用水稀释至刻线，摇匀，作为浸提剂待用。称取100 g样品，置于2 L提取瓶中，根据样品的含水率，按液固比为201(L/kg)计算所需浸提剂的体积，加入浸提剂，盖紧瓶盖后固定在翻转式振荡器上，调节转速为(30±2) r/min，于(23±2) ℃下振荡(18±2) h。在压力过滤器上装上0.6 μm的玻纤滤膜，用稀硝酸清洗滤膜和过滤装置，打开空压机并进行过滤，所得滤液即为浸出液。

Retailers hated the term but then tried to reinvent it. It was the day their profits went from red to black — so they said.

在地震作用下，渡槽内水体剧烈紊动，水面急剧变化，需要采用精细的紊流模型。RNG-紊流模型通过大尺度运动和修正后的黏度项体现小尺度的影响，使小尺度运动系统地从控制方程中去除，可以更好地处理高应变率及流线弯曲程度较大的流动[35-36]。

2 结果与分析

2.1 水位

考虑到水位变化可能会造成渡槽满溢，选取渡槽中间截面（中=50 m）靠近左、右边壁处（左=0.244 m和右=3.256 m）的水位进行分析。

由图6可知，靠近自由液面处水体垂直边壁加速度远大于渡槽中部和底部加速度，以“竖直水平”情况为例，靠近自由液面处水体垂直边壁加速度分别是渡槽中部和底部加速度的13.8倍和11.9倍，说明靠近自由液面处水体受地震作用响应更剧烈，则靠近自由液面处渡槽边壁受到水体垂直作用力最大。

表3 设计流量3种地震荷载最大水位汇总

对比设计流量、加大流量2种不同流量工况下的左边壁处水位变化过程，如图5所示。由图5可得，设计流量与加大流量水位峰值出现时间大致相同，但加大流量工况下水位明显高于设计流量工况，前者左边壁最大水位相比后者抬升了9.4%。因此加大流量工况下水体漫顶的风险增大。

对比4种代表频率（=1.49、4.20、5.78、9.70 Hz）对应的地震加速度作用下的最大水位如图4所示。由图4可知，对于4种频率，左右边壁最大水位均存在以下大小关系：H=4.20Hz>H=5.78Hz>H=1.49Hz>H=9.70Hz。由大小关系可知，随着频率的增加，水体响应剧烈程度先增大后减小，说明在=1.49～5.78 Hz区间，存在对水体运动影响最为显著的频率。其中“=4.20 Hz”情况右边壁最高水位比“=9.70 Hz”情况仅增大了1.08%，则频率的改变对于最高水位变化影响微弱。

图4 典型频率地震荷载作用下左右边壁最大水位变化

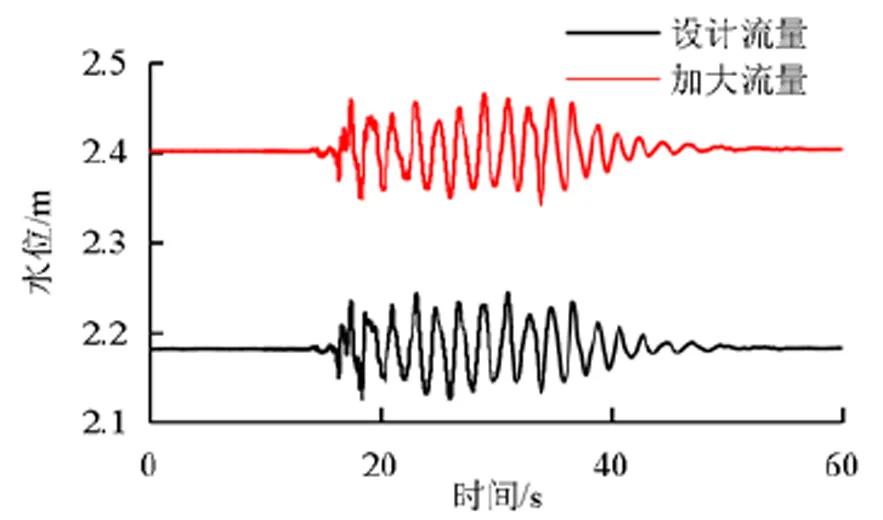
图5 不同流量工况下左边壁水位变化过程

2.2 加速度

由于KOYNA地震波[29-30]关于水平方向和竖直方向的加速度资料较完整，可以较好地应用于仿真模拟，论文将其作为典型地震荷载，分别在设计流量工况、加大流量工况下对渡槽施加地震荷载。关于地震荷载的施加，分别从地震荷载作用方式、地震荷载频率、渡槽内水体流量大小3个角度出发，设立了3类对照组，通过分析对比仿真计算中的水位和垂直边壁加速度结果，得到对渡槽施加不同方向的地震荷载、不同频率的地震荷载、以及同一地震荷载作用下不同流量工况渡槽内水体的响应特性。

对比4种代表频率（=1.49 Hz，4.20 Hz，5.78 Hz，9.70 Hz）对应的地震加速度作用下渡槽左边壁各代表点处与左边壁法线方向相反（-方向）的最大垂直边壁加速度如图7所示。由图7可知，对于4种频率，左边壁均存在大小关系为：a=4.20 Hz>a=5.78 Hz>a=9.70 Hz且a=4.20 Hz>a=1.49 Hz>a=9.70 Hz，与最大水位随频率的变化存在类似的规律，再次说明在=1.49～5.78 Hz区间,存在对水体运动影响最为显著的频率。随着水位的抬升，各代表位置处“=4.20 Hz”情况左边壁-方向最大垂直边壁加速度分别为“=9.70 Hz”情况的2.6、2.7倍以及3.5倍，则频率的改变对于垂直边壁最大加速度的变化影响显著。

对比设计流量工况下单独施加竖直地震荷载、单独施加水平地震荷载、同时施加竖直水平地震荷载3种情况渡槽代表位置处的水位分布，统计不同情况下的最大水位如表3所示。由表3可知，只施加竖直方向地震加速度时，左右边壁最大水位相较另外两种情况水位抬升幅度较小。其中“水平方向”情况左右边壁最高水位均比“竖直方向”情况增大了2.5%，而“竖直水平”情况左边壁最高水位相比“水平方向”情况仅增加0.1%，其右边壁最高水位不增反降，说明竖直方向加速度的加入相较水平方向加速度对水体影响较为微弱。

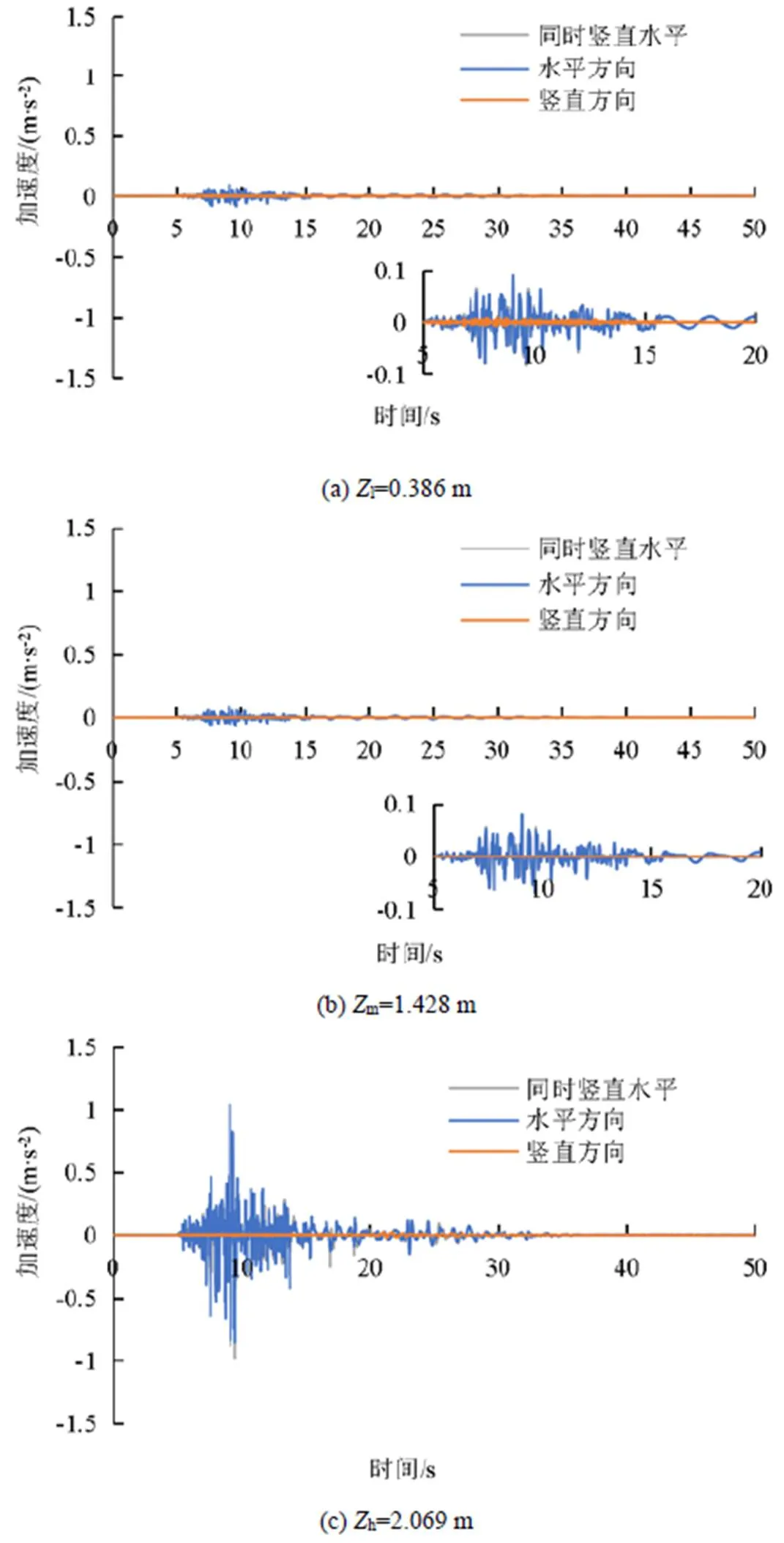
图6 3种地震荷载作用下代表位置处垂直边壁加速度变化

表4 3种荷载作用下-x方向垂直边壁加速度最值对比

而对比表4，在渡槽底部、中部和靠近自由液面处，“水平方向”情况水体在左边壁的-方向加速度最值分别是“竖直方向”情况的10.5、95.0倍和40.9倍，说明水体在水平方向地震荷载作用下运动更剧烈。另外，随着水位的抬升，3个代表位置处“同时竖直水平”情况垂直边壁加速度最值较“水平方向”情况增大了5.07%、4.80%和10.83%，说明2个方向地震荷载同时作用产生的水体响应较某一方向单独作用时的水体响应更大。

由于KOYNA地震震中烈度为Ⅷ-Ⅸ度，而选用的渡槽模型则位于设防烈度为Ⅵ度的地震区，为了适应渡槽的工程背景，论文按照烈度比例对地震进行线性缩放。另外，同时考虑水平方向和竖直方向地震作用时，地震作用总效应等效于竖直地震作用乘以0.5的遇合系数后与水平地震作用的叠加[1]。原始KOYNA地震方向（渡槽横截面水平方向）和方向（渡槽横截面竖直方向）加速度图以及缩放后的方向与缩放且0.5倍折减的方向地震加速度如图2所示。

对比设计流量工况下单独施加竖直地震荷载、单独施加水平地震荷载、同时施加竖直水平地震荷载3种情况渡槽代表位置处的垂直边壁加速度分布，得到3种地震荷载作用下垂直边壁加速度变化如图6所示。另外统计不同荷载作用下、与渡槽左边壁内侧法线方向相反（-方向）的最大垂直边壁加速度，汇总得到表4，表4中加速度下标1、2、3分别对应单独施加竖直地震荷载、单独施加水平地震荷载、同时施加竖直水平地震荷载3种情况的计算结果。

对比设计流量工况和加大流量工况渡槽水体垂直边壁加速度结果，保证渡槽尾端水深不变，在“同时竖直水平”地震波组合作用下，统计渡槽左边壁各代表点处与左边壁法线方向相反（-方向）的最大垂直边壁加速度，汇总得到表5。由表5可知，随着水位抬升，各代表点处加大流量工况下-方向加速度最大值分别为设计流量工况的0.8、0.7倍和0.2倍，说明流量增大会削减加速度峰值，减小水体对渡槽边壁的作用力。

(一)社会热点事件。由于某一事件成为人们关注的社会热点，因而人们制造出许多与之相关的词语并在网络交流中广泛运用。如：

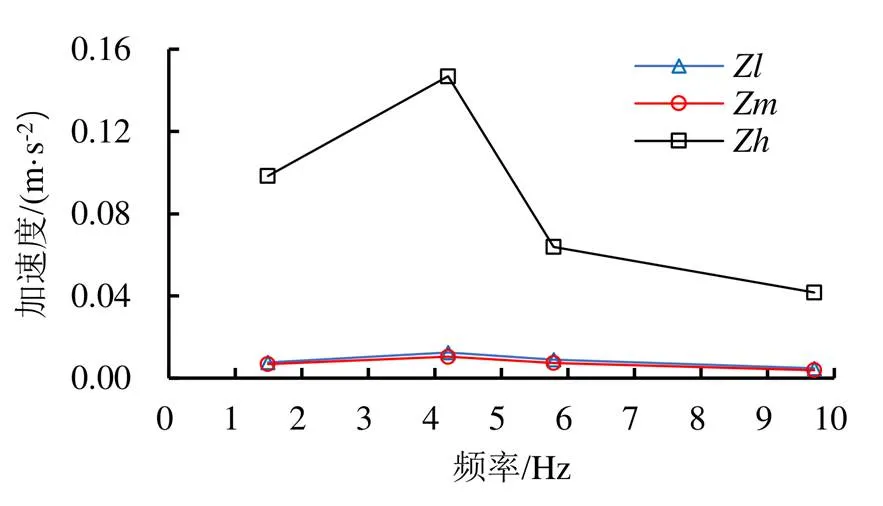
图7 典型频率地震荷载作用下左边壁-x方向最大垂直边壁加速度变化

表5 不同工况水体垂直边壁加速度-x方向最大值

3 讨论

此前分析渡槽结构的方法主要有Westergaard[9]的附加质量模型，Housner[11]的等效质量-弹簧模型，Hirt等[18]创立的ALE法等。上述方法或忽略水体的压缩性与紊动作用，或存在使用的局限性且对部分渡槽计算结果偏危险，或建模过程烦冗计算成本消耗过巨。且以上方法均未模拟真实流体，而采用简化建模近似代替槽内水体。但地震作用下渡槽与槽内水体的耦合过程中槽内水体为动态边界，若要了解其动态变化规律，则需对渡槽内水体建模以更直观地得出该动态边界的变化特性。

本研究根据某新建灌区渡槽尺寸设计了模型，并基于FLOW-3D软件对典型地震荷载作用下的渡槽水体进行仿真，以分析其水力特性。相比前人对渡槽-水耦合模型进行简化的近似处理[9-25]，本研究则直接对地震工况下的渡槽水体进行建模分析，进而得出渡槽内的流体动态边界变化规律，建模过程相对简单，计算成本不高，更易推广，且可以为渡槽振动条件下的流固耦合分析提供重要依据。由仿真结果得出，地震作用下，渡槽内水体的运动与地震荷载的方向、地震荷载的频率以及流量大小有关。靠近自由液面处，水体对渡槽边壁的作用力最大，在结构设计时应考虑自由液面附近的渡槽边壁强度。对于现有的水工建筑物抗震设计规范关于渡槽的抗震措施，本研究建议在八级以上的水平方向地震计算时考虑附加水压力荷载，以保证渡槽设计的安全性。另外，渡槽流量增大虽然会减小水体对边壁的作用力，但其导致的渡槽漫顶风险仍不容忽视。

本研究仍然存在一些待改进的地方：论文在渡槽建模时对渡槽模型进行了简化处理，没有考虑包括排架在内的下部结构在地震作用时对上部结构的影响，在之后的研究中需要对渡槽模型进一步优化，对渡槽的下部结构合理建模，使得计算结果更贴合实际值；论文在设置地震工况时对地震荷载的施加过程进行了简化处理，将水平、竖直方向地震加速度直接作用在渡槽上，而忽略了不同方向地震波传播的滞后性，在后续的研究中需要对地震荷载施加过程逐步细化，使结果在实际工程中更具应用性；论文在设置流量工况时未考虑流量小于设计流量的情况，这是因为研究地震荷载时，当流量低于设计流量，渡槽与水体间的耦合作用相对较弱，且水体不会出现满溢的风险，在后续的研究将考虑渡槽施加风荷载的情况，则需要对渡槽在设计流量的75%、50%、25%工况的水力特性进一步分析说明。

4 结论

1）针对本文仿真的各种工况，均存在靠近自由液面处渡槽边壁受到水体垂直作用力最大的情况。其中靠近自由液面处水体垂直边壁加速度均为渡槽中部和底部垂直边壁加速度的10倍以上。

2）施加单一方向地震荷载时，水平方向地震荷载比竖直方向对水体作用更显著。其中前者水面波动比后者增大了2.58%。

3）同时施加2个方向地震荷载时，水体响应较某一方向单独作用时更大。相比单一方向地震荷载作用，同时施加两个方向地震荷载时相同位置处的垂直边壁作用力增大了5%～10%。

4）改变地震荷载频率，随着频率的增大，水体紊动剧烈程度先增加后减小，并在一定区间内存在使得水体运动最为剧烈的频率。论文选取了=0～12.5 Hz的频率区间中4个代表频率对应的地震加速度进行仿真，在渡槽底部、中部和靠近水面处，“=4.20 Hz”情况左边壁-方向最大垂直边壁加速度为“=9.70 Hz”情况的2.5～3.5倍。

5）改变水体流量，流量的增大会削弱水体对边壁的垂直作用力，但此时因水位更高，水体漫顶的风险增加。在渡槽底部和中部加大流量工况加速度最大值比设计流量工况减小了20%以上，而在靠近水面处前者仅为后者的0.2倍。

[1] 陈德亮,夏富洲,陈尧隆. 水工建筑物[M]. 第5版. 北京：中国水利水电出版社, 2008: 32-377.

CHEN Deliang, XIA Fuzhou, CHEN Yaolong. Hydraulic Structures [M]. 5th Edition. Beijing: China Water Power Press, 2008: 32-377.

[2] 冯晓波, 王长德, 管光华. 大型渡槽温度场的边界条件计算方法[J]. 南水北调与水利科技, 2008, 6(1): 170-173.

FENG Xiaobo, WANG Changde, GUAN Guanghua. Boundary condition calculation method of temperature field in large-scale aqueduct[J]. South-to-North Water Transfers and Water Science & Technology, 2008, 6(1): 170-173.

[3] 宋书卿, 王长德, 冯晓波, 等. 空心渡槽的温度应力研究[J]. 中国农村水利水电, 2005(11): 86-88,90.

SONG Shuqing, WANG Changde, FENG Xiaobo, et al. Research on thermal stress of cavity aqueduct[J]. China Rural Water and Hydropower, 2005(11):86-88,90.

[4] 周云, 房艳国, 王家祥, 等. 滇中引水工程穿过活动断裂防震抗震思路研究[J]. 三峡大学学报(自然科学版), 2019, 41(S1): 7-11.

ZHOU Yun, FANG Yanguo, WANG Jiaxiang, et al. Earthquake resistanceand prevention methodsof tunnels through active faultsof water diversion projectin central Yunnan [J]. Journal of China Three Gorges University ( Natural Sciences), 2019, 41(S1): 7-11.

[5] 水工建筑物抗震设计标准. GB 51247—2018[S].

Standard for seismic design of hydraulic strcutures. GB 51247—2018[S].

[6] 季日臣, 夏修身, 陈尧隆. 水体晃荡作用对渡槽横向抗震影响的研究[J]. 水力发电学报, 2007(6): 30-34.

JI Richen, XIA Xiushen, CHEN Yaolong. Research on influence of water shake acting on aqueduct transverse seismic response[J].Journal of Hydroelectric Engineering, 2007(6): 30-34.

[7] 李遇春, 楼梦麟, 周成. 大型渡槽的竖向地震效应分析[J]. 地震工程与工程振动, 2008, 28(2): 102-107.

LI Yuchun, LOU Menglin, ZHOU Cheng. Analysis of vertical seismic effects for large -scale aqueduct bridges[J]. Earthquake Engineering and Engineering Vibration, 2008, 28(2): 102-107.

[8] 彭辉, 刘德富, 罗先启. 南水北调中线漕河渡槽流固耦合机理研究[J]. 灌溉排水学报, 2006(5): 75-77.

PENG Hui, LIU Defu, LUO Xianqi. Study on the fluid-solid interaction mechanism of caohe aqueduct in South-to-North Water diversion middle line project[J]. Journal of Irrigation and Drainage, 2006(5): 75-77.

[9] WESTERGAARD H M. Water pressures on dams during earthquakes[J]. Transactions of the American Society of Civil Engineers, 1933, 98(2): 418-433.

[10] 高兑现, 李正农, 唐永胜, 等. 渡槽结构地震反应分析[J]. 水力发电学报, 2004,23(5): 40-43,31.

GAO Duixian, LI Zhengnong, TANG Yongsheng, et al. Anti-seismic analysis of aqueduct structure[J]. Journal of Hydroelectric Engineering, 2004, 23(5): 40-43,31.

[11] HOUSNER G W. Dynamic Pressure on Accelerated Fluid Containers[J]. Bulletin of the Seismological of America, 1957,47(1): 15-35.

[12] 季日臣, 夏修身, 陈尧隆, 等. 考虑流-固耦合梁式矩形渡槽横向地震响应研究[J]. 地震学报, 2007,29(3): 328-334,337.

JI Richen, XIA Xiushen, CHEN Yaolong, et al. Transverse seismic response of beam aqueduct considering fluid-structure coupling[J]. Acta Seismologica Sinica, 2007, 29(3): 328-334,337.

[13] 张多新, 王清云, 白新理. 地震作用下大型渡槽动力响应分析研究[J]. 水力发电, 2008, 34(6): 51-54.

ZHANG Duoxin, WANG Qingyun, BAI Xinli. Research on the Dynamic Response Analysis of Large Scale Aqueduct under Seismic Action[J]. Water Power, 2008, 34(6): 51-54.

[14] 刘云贺, 胡宝柱, 闫建文, 等. Housner模型在渡槽抗震计算中的适用性[J]. 水利学报, 2002 (9): 94-99.

LIU Yunhe, HU Baozhu, YAN Jianwen, et al. Applicability of Houser Model to aseismic characteristics calculation of aqueduct[J]. Journal of Hydraulic Engineering, 2002 (9): 94-99.

[15] NORDEN H, ZHENG S, STEVEN R L, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[M]. London: Royal Society, 1998:904-962.

[16] 张建伟, 江琦, 曹克磊, 等. 基于二次滤波的HHT渡槽模态参数辨识方法[J]. 农业工程学报, 2015, 31(15): 65-71.

ZHANG Jianwei, JIANG Qi, CAO Kelei, et al. HHT modal parameter identification for aqueduct based on secondary filtering[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(15): 65-71.

[17] 张建伟, 付杰, 赵瑜, 等. 水体-结构-地基耦联的泵站出水塔地震响应分析[J]. 农业工程学报, 2018, 34(11): 128-135.

ZHANG Jianwei, FU Jie, ZHAO Yu, et al. Seismic response analysis of outlet tower based on water-structurefoundation coupling system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(11): 128-135.

[18] HIRT C W, AMSDEN A A, COOK J L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds[J]. Journal of Computational Physics, 1974, 14(3): 227-253.

[19] 吴轶, 莫海鸿, 杨春. 大型矩形渡槽-水耦合体系的动力性能分析[J]. 地震工程与工程振动, 2004(4): 137-142.

WU Yi, MO Haiou, YANG Chun. Dynamic characteristics of large rectangular aqueduct-water coupling system[J]. Earthquake Engineering and Engineering Vibration, 2004(4): 137-142.

[20] 吴轶, 莫海鸿, 杨春. U形渡槽水体大幅晃动的ALE有限元模拟[J]. 华南理工大学学报(自然科学版), 2003(9): 90-93.

WU Yi, MO Haihong, YANG Chun. ALE Simulation of large sloshing of water in U-shaped aqueduct[J]. Journal of South China University of Technology(Natural Science Edition), 2003(9): 90-93.

[21] 李遇春, 楼梦麟, 尚伟, 等. 大型渡槽抗震分析中流体的位移有限元模式[J]. 水利学报, 2003(2): 93-97.

LI Yuchun, LOU Menglin, SHANG Wei, et al. Displacement-based fluid finite element for seismic-resistant analysis of large-scale aqueduct[J]. Journal of Hydraulic Engineering, 2003(2): 93-97.

[22] 张多新, 王清云, 刘东常. 基于FSI系统的(ui, p)格式大型渡槽动力分析[J]. 长江科学院院报, 2009, 26(2): 41-44,47.

ZHANG Duoxin, WANG Qingyun, LIU Dongchang. Dynamic analysis of large aqueduct based on format (ui, p)of FSI System[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(2): 41-44,47.

[23] 李遇春, 楼梦麟. 强震下流体对渡槽槽身的作用[J]. 水利学报, 2000(3): 48-54,60.

LI Yuchun, LOU Menglin. Action of fluid on aqueduct body during strong earthquake[J]. Journal of Hydraulic Engineering, 2000(3): 48-54,60.

[24] 张多新, 王清云, 白新理. 大型渡槽结构动力学研究进展[J]. 自然灾害学报, 2011, 20(4): 22-30.

ZHANG Duoxin, WANG Qingyun, BAI Xinli. Research progress in structural dynamics of large scale aqueduct[J]. Journal of Natural Disasters, 2011, 20(4): 22-30.

[25] 张文学, 黄荐, 陈盈, 等. 渡槽结构考虑流固耦合的横向地震响应简化计算公式[J]. 工程力学, 2017,34(8): 69-75,95.

ZHANG Wenxue, HUANG Jian, CHEN Ying, et al. A Simplified formula for the calculation of the transverse seismic response of aqueducts considering fluid-structure interaction[J]. Engineering Mechanics, 2017, 34(8):69-75,95.

[26] 赵昕, 张晓元, 赵明登, 等. 普通高等教育“十一五”规划教材水力学[M]. 北京: 中国电力出版社, 2009:181-185.

ZHAO Xin, ZHANG Xiaoyuan, ZHAO Mingdeng, et al. Textbooks for the eleventh five-year plan for general higher education Hydraulics[M]. Beijing: China Electric Power Press, 2009: 181-185.

[27] 刘英, 王文娥, 胡笑涛. 基于CFD的U形渠道量水柱体型比选研究[J]. 灌溉排水学报, 2014,33(Z1): 163-167.

LIU Ying, WANG Wen’e, HU Xiaotao. Comparison of water-measuring column in U-shaped channel based on CFD[J]. Journal of Irrigation and Drainage, 2014,33(Z1): 163-167.

[28] 冉聃颉, 王文娥, 胡笑涛. 梯形喉口无喉道量水槽设计及其水力性能模拟与试验[J]. 农业工程学报, 2017,33(15): 177-183.

RAN Danjie, WANG Wen’e, HU Xiaotao. Design of trapezoidal cut-throated flume and its hydraulic performance simulation and test[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(15): 177-183.

[29] LEE J, FENVES G L. Plastic-damage Model for Cyclic Loading of Concrete Structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900.

[30] YADAV A, BANSAL B K, PANDEY A P. Five decades of triggered earthquakes in Koyna-Warna Region, western India – A review[J]. Earth-Science Reviews, 2016, 162: 433-450.

[31] 孙耀充. 曲线风格有限差分模拟地震波在各向异性介质和固—液耦合介质中的传播[D]. 合肥:中国科学技术大学, 2017.

SUN Yaochong. Numerical simulation of seismic wave propagation in anisotropic media and fluid-solid media by curvilinear grid finite difference method[D]. Hefei: University of Science and Technology of China, 2017.

[32] 吴天行, 华宏星. 机械振动[M]. 北京: 清华大学出版社, 2014: 132-137.

WU Tianxing，HUA Hongxing. Mechanical Vibration [M]. Beijing: Tsinghua University Press, 2014: 132-137.

[33] 杨峥. 基于FLOW-3D的U型渠道板式流量测量装置有限元分析[J]. 广东水利水电, 2018(12): 69-74.

YANG Zheng. Study on Hydraulic Characteristics of U-Channel channel flow measuring device based on FLOW-3D[J]. Guangdong Water Resources and Hydropower, 2018 (12): 69-74.

[34] 李绍武, 尹振军. N-S方程的数值解法及其在水波动力学中应用的综述[J]. 海洋通报, 2004(4): 79-85.

LI Shaowu, YIN Zhenjun. Review on the research of the numerical solvers to N-S equation and their applications in water wave hydrodynamics[J]. Marine Science Bulletin, 2004 (4): 79-85.

[35] 朱亚磊, 马孝义, 战国隆, 等. 平坦V形量水堰的数值模拟[J]. 人民黄河, 2010,32(6): 98-99,101.

ZHU Yalei, MA Xiaoyi, ZHAN Guolong, et al. Numerical simulation of flat V-shaped weir[J]. Yellow River, 2010, 32(6): 98-99,101.

[36] 李福宝. 流体力学[M]. 北京: 冶金工业出版社, 2010: 158.

LI Fubao. Hydrodynamics[M]. Beijing: Metallurgical Industry Press, 2010: 158.

Numerical Simulation of Earthquake-induced Water Dynamic in Aqueduct

YANG Mengwei,GUAN Guanghua*

(State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

【】Aqueduct is a watercourse to carry away water from its source to distributing points, and its operation and safety are affected by many factors. The purpose of this paper is to analyze the response of water dynamics in the aqueduct to seismic load in an attempt to help aqueduct design under different scenarios.【】The analysis was based on numerical simulations. The seismic load was characterized by loading mode and loading frequency. The three-dimensional free-surface water flow in the aqueduct under different flow rate as affected by different combinations of loading characteristic factors was simulated using the FLOW-3D software, from which we calculated the force imposed by the flowing water to the aqueduct. 【】The maximum vertical force induced by the seismic load was at the edge wall of the aqueduct proximal to the free water surface, which was more than ten-fold that at the bottom and in the midst of the aqueduct. When the seismic load was imposed in a single direction, the force induced by it to the aqueduct was 2.5%higher in the horizontal direction than in the vertical direction. With the frequency of seismic load increasing, the intensity of water body movement increased first and then declined when the frequency exceeded a threshold value. 【】Designing aqueducts potentially subject to seismic load should consider the strength of the side wall near the free water surface. While an increase in water flow rate reduces the force imposed by the water body to the side-walls under seismic load, it could risk overflow.

aqueduct; seismic load; numerical simulation; free water surface; acceleration of vertical sidewall

TV135.3

A

10.13522/j.cnki.ggps.2020510

1672 - 3317（2021）07 - 0089 - 08

杨梦薇, 管光华. 地震作用下渡槽内水体响应三维数值模拟与分析[J]. 灌溉排水学报, 2021, 40(7): 89-96.

YANG Mengwei, GUAN Guanghua. Numerical Simulation of Earthquake-induced Water Dynamic in Aqueduct[J]. Journal of Irrigation and Drainage, 2021, 40(7): 89-96.

2020-09-11

国家自然科学基金项目（51979202，51009108）；“十三五”国家重点研发项目（2016YFC0401810）

杨梦薇（1997-），女。硕士研究生，主要从事灌排自动化和水力除藻研究。E-mail:yangmengwei@whu.edu.cn

管光华（1979-），男，江苏人。硕士生导师，博士，主要从事渠道系统自动化运行调度理论与技术、量水理论与方法、排工程新结构方面的研究。E-mail: GGH@whu.edu.cn

责任编辑：韩 洋