化“静”为“动”：提升学生的数学转化能力

张超

[摘 要]与几何图形有关的动态变化题已成为教学热点之一，这类问题有助于培养学生的自主探索精神和创新意识。在“滚动圆的周长和面积”教学中，利用转化思想解决由静态圆到动态圆，圆的运动轨迹所形成的周长和面积这一类问题，从而提升学生的数学转化能力。

[关键词]滚动圆;运动轨迹;转化能力

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）20-0078-02

转化思想贯穿“空间与几何”的教学过程，在小学数学教材中，处处可寻到转化思想的身影。如推导圆的面积公式时，可以通过对圆进行割补、拼接，转化成已学过的图形，这就是运用转化思想将不熟悉的知识转化为已学过的知识，将新知与旧知联系起来，从而加深理解。如何让学生将转化思想运用到实际问题中呢？这是笔者一直在思考的问题。

下面笔者以“滚动圆的周长和面积”教学为例，从学生的实际能力出发，谈谈如何提升学生的转化思想。

一、化曲为直导入课堂，初步渗透转化思想

新课程背景下的练习课，要深入研究课程标准、教材，落实“四基”要求，教师应熟做每一道例题和习题，深入分析例题和习题所蕴含的知识点，关注习题与例题的匹配性与关联性，分析习题的难度。在设计题目的同时，充分考虑知识的形成线索和学生学习的认知线索，不能高于学生的实际能力，也不能是简单的重复训练，而是要考虑到题目的层次性、可行性、全面性和发展性。

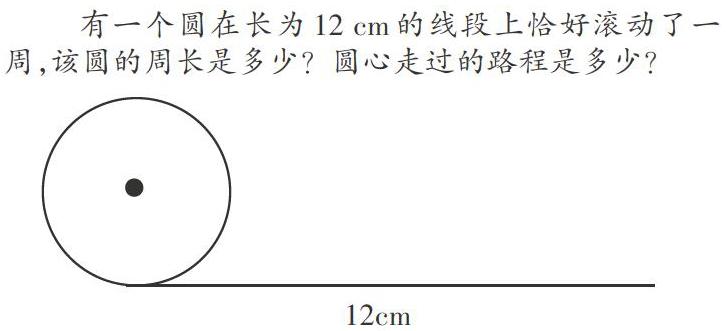
在复习导入环节，打破常规，不再直接给出圆的半径或直径来求圆的周长，而是告诉学生“有一个圆在长为12 cm的线段上恰好滚动了一周”，这会勾起学生回忆。在教学圆的周长时，就是利用了“滚动法”探究出圆的周长计算公式，同时渗透“化曲为直、化未知为已知”的思想，教会学生数学不仅仅要学会计算，更要了解其中的数学思想。

解决完第一个问题之后，再看第二个问题：圆心走过的路程是多少？聪明的学生通过观察就可以发现：圆从起点出发，滚动一周到终点，圆心走过的路程恰好是这条线段的长度，也就是12 cm。通过这两个问题，学生不再机械地套公式、代数据、算得数。这样的导入环节能大大调动学生的学习积极性，使之乐于开动脑筋多思考，打开思维。

二、练习设计由浅入深，充分运用转化思想

练习应该要有系统性和层次性，要符合由易到难、由浅入深的规律，习题应该少而精。在“滚动圆的周长和面积”的练习课中，改变传统的方式，以题组模式为主线，一步一步提升难度。

1.求同思变，探究圆心走过的路程

把圆在直线上滚动转到在一个平面图形上滚动，在滚动过程中，有学生就发现：在平面图形的边上，圆还是沿直线滚动，但是滚动到角上时，圆不能再往前滚动了，而是要“转弯”，去另外一条边上继续滚动，如此重复，直到回到起点才停下来不再滚动。在这个过程中，圆心的运动轨迹不再完全是直的了，而是在每个角上会形成一段弧线。学生再结合扇形的知识，便恍然大悟：原来在每个角上形成的弧线拼起来就是一个完整的圆;直边加起来就是所绕图形的周长。从而得出结论：圆心的运动轨迹=圆的周长+所绕图形的周长。把学生非常熟悉的“圆在直线上滚动”转变成“绕着平面图形滚动”，把不熟悉的运动轨迹转化为学生熟悉的，问题也就迎刃而解了，同时也培养了学生求同思变的思维。

2.由线到面，掌握圆扫过的面积

题组二是在题组一的基础上展开的，由于学生已经有了题组一的练习经验，有一定的空间观念，可以先放手让学生思考，猜一猜圆片扫过的是什么图形？学生在脑海中形成动图的画面，再画出运动轨迹讨论，尝试得出结论。圆扫过的面积分成两个部分，一部分在平面图形直边上形成的是长方形，长方形的长是该直边的长度，宽是圆的直径，所以形成的所有长方形的面积总和=平面图形的周长×直径;另一部分是在每个角上扫过形成的图形都是扇形，由题组一知道，每个角上的扇形拼起来就是一个完整的圆。这样的推理过程，既锻炼了学生的空间想象能力和动手操作能力，又培养了学生的概括能力和小组合作意識。

该组练习的模型与题组一的模型完全一致，题组一要研究的是圆心的运动轨迹，连点成线，求周长;而题组二虽然是相同的模型，运动轨迹也都一致，但是要求的是面积。前后两个题组紧紧衔接在一起，由点到线，由线到面，环环相扣，学生的思维也由浅入深。

三、追本溯源题组设计，初步形成反思意识

本节课适合在学生学完圆的周长和面积之后教学，进行课后拓展。通过变式题，将圆绕不同封闭图形外面滚动时圆心走过的路程的计算方法进行统一。在此基础上，对比圆在长方形外滚动和圆在长方形内滚动这两种不同情况，提炼圆在长方形内滚动时圆心的经过路线和圆扫过的面积的计算方法。

习题一方面是考查学生对周长和面积意义的理解，帮助学生巩固圆的周长及面积的计算方法;另一方面是通过图形形状的变化与解决策略不变渗透思想方法，以及通过图形形状不变而圆的位置改变，引导学生找出圆在不同平面图形外滚动时的内在联系，体会圆在同一个图形内外滚动时的本质区别。

教师在“滚动圆的周长和面积”的教学过程中，应当结合实际教学内容，从学生的已有知识出发，通过多种多样的变式训练，不断渗透并深化转化思想，从而让学生了解、掌握和运用转化思想，发展空间观念，形成数学思维，提高转化能力。

（责编 黄 露）