海啸波与环形岛礁相互作用及致灾机理研究

黄嘉豪，朱刘杰，崔庆宇，樊 煜，倪兴也

（河海大学 港口海岸与近海工程学院，江苏 南京 210098）

0 引言

海啸波是自然界中破坏性最强的灾害之一，由于海啸波波长往往长达上百公里，因此在深水大洋中传播速度极快，对于近岸航行中的船只威胁较大且难以提前预警，不仅会造成巨大的财产损失，还会导致人员伤亡。因此，研究海啸波与环礁之间的相互作用具有重要的意义。由于海啸波的首波与孤立波类似，本文采用孤立波来模拟海啸波的传播［1］。

国内外学者对于孤立波在近岸区域的变形做了 许 多 深 入 的 研 究，温 鸿 杰 等［2－3］通 过 在SPH（Smoothed Particle Hydrodynamics）模 型 中引入动量源函数和人工速度衰减函数来稳定生成和吸收规则波与随机波，并研究了随机波在岸礁上的传播规律。姚宇等［4］基于Navier-Stokes方程通过OpenFOAM程序采用大涡模拟法（LES）模拟湍流和修正的流体体积法（VOF）捕捉自由液面，研究了孤立波在岛礁的传播与变形。房克照等［5］基于高阶Boussinesq方程建立了数学模型模拟了孤立波在潜礁地形上的传播与变形。高睿等［6］通过SPH方法研究了孤立波沿斜坡堤的传播、变形与破碎过程。但在海啸波对环礁的相互作用尤其是对环礁上建筑物以及礁湖内船只的影响方面仍然研究较少。DualSPhysics是一款开源的弱可压流体模型，常用于海岸工程问题的研究［7］。本文基于DualSPhysics，采用无网格的SPH方法构建了一个能模拟孤立波与概化环礁地形相互作用的数值模型，通过设置多组不同地形条件与礁坪水深来研究孤立波在环礁上的传播与演化过程，通过放置浮体的方式来探究海啸波对建筑物与船只的作用。

1 数值模型简介

SPH方法是一种拉格朗日无网格方法，相比基于欧拉方法的有网格模型，其在模拟波浪破碎、翻卷等大变形具有显著的优越性，可以避免大变形时由于网格扭曲而影响精度。对于极端波浪与环礁地形的相互作用问题，流体自由表面变形剧烈，因此选用SPH方法进行数值模拟能得到更高的准确性。

SPH方法的基本思想是将连续的流体介质离散为一系列的微粒，每个粒子具有如密度、质量、速度等一系列物理量，通过追踪每个粒子的运动来推求整个系统的物理特性。

1.1 SPH方法基本原理

在SPH方法中，对任意一个场函数，其积分近似都可以表示为

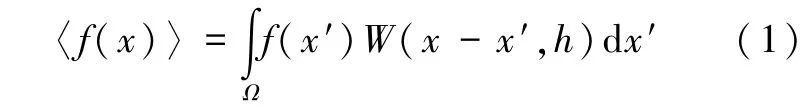
式中，＜f（x）＞为函数f（x）的近似值，x为位置矢量，W（x－x′，h）为一种加权函数或者核函数，h为光滑长度。SPH方法最终要将函数的积分近似表达式转化为所有粒子叠加求和的离散化形式，使流体被离散为数量有限的粒子，每个粒子具有独立的物理属性，离散化后的函数积分表达式可变为：

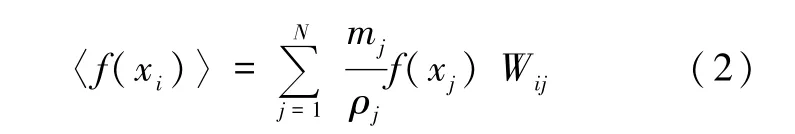
式中，mj、ρj分别为j粒子的质量与密度，Wij＝W（xi－xj，h），即对函数f（x），其在任意一点处的函数值可以通过光滑函数对其光滑长度h内的所有粒子插值求和获得。

1.2 控制方程

本文采用的SPH 水动力学模型通过求解Navier-Stokes方程来模拟水体的强非线性运动过程，其中拉格朗日形式的动量方程为：

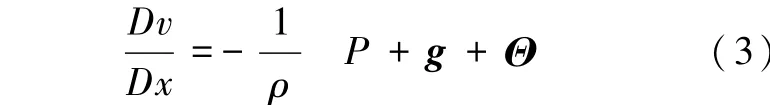
式中，Θ为耗散项。

在弱可压缩SPH模拟的整个过程中每个粒子的质量保持不变，只有密度发生微小的波动。这些密度变化是通过求解连续性方程获得：

在SPH方法中流体被视为弱可压缩流体，并通过状态方程根据粒子密度确定流体压力

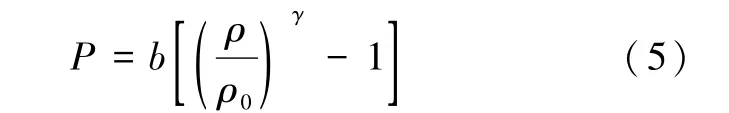
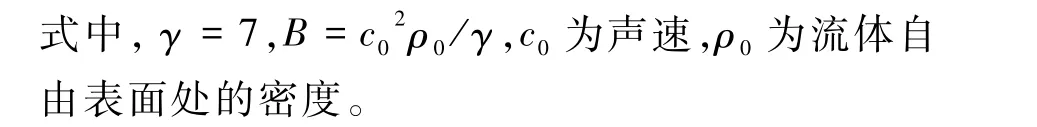
本文采用动力学边界条件DBC（Dynamic Boundary Condition），该边界条件下边界粒子的控制方程与流体粒子相同，当流体粒子与边界粒子间的距离小于光滑半径时，边界粒子将产生对流体粒子的排斥力，同时边界粒子的密度和压力将增加。

2 模型设置

采用DualSPhysics构建数值波浪水槽，水槽尺寸为850m×100m×60m（长×宽×高），如图1所示。其中左端设置一造波板，用于生成孤立波；中部的环礁地形概化为向海坡、礁坪、潟湖坡、潟湖4个部分。环礁坡脚距造波板200m，礁坪长度为200m，潟湖坡坡度统一为1∶5，由于研究的是海啸波在近海区域传播，因此外海水深取10m，礁坪高度也取10m，潟湖内水深参照永乐环礁三维DEM（Digital Elevation Model）在2～40m中选取［8］，考虑到模型范围未包括潟湖中心水深较深的地区，因此选择10m作为代表。外海段波高测点间隔50m 布置，向海坡段波高测点间隔10m布置。潟湖内则在潟湖坡脚处和距坡脚50m处布置两处测点，水槽末端800～850m处设置阻尼消波区，用以消除反射波。

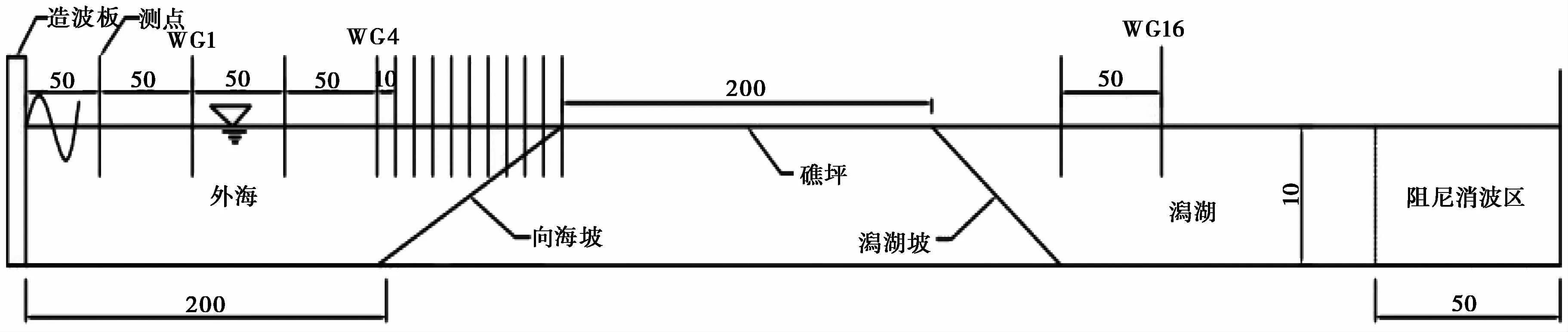
图1 孤立波在环礁地形上传播模型示意图Fig.1 Schematic diagram of solitary wave propagation model on atoll topography

外海段布置波高测点4个，从50～200m间隔50m布置，潟湖段由于模型坡度有变化导致长度不一，因此将波高测点沿高程布置，高程每上升0.5m布置一波高测点，直至礁坪。礁坪段上沿途每隔10m设置波高测点与流速测点。潟湖坡上在距离坡脚10m处间隔10m布置7个测点，用以研究礁坪上的涌波对潟湖的影响。

2.1 数值模型收敛性分析

设置4组粒子间距不同的算例，用以分析SPH方法中粒子间距与数值模拟精度的关系，即模型的收敛性。考虑到计算效率，4组算例入射波高均为8m，粒子间距 dp分别取0.08m、0.15m、0.12m 和 0.10m，粒 子 数 量 分 别 为1339596个、378417个、601602个和858146个。波高数据来自距造波板200m 处的测点。数据处理时横坐标取时间，纵坐标取自由液面高程。数值模拟波面沿时间变化如图 2所示。在8.66～8.98s前后孤立波发生剧烈变形，波前端变陡至几乎与静水面垂直，随后波峰向下翻卷呈舌状投入水中，随后波浪在传播过程中多次破碎，呈现出强非线性。在200m 处，上一次波浪破碎后投入水体的水舌使得波浪前端的水体壅高，壅高水体首先在17.98s时通过测点，随后破后波波峰在18.62s时通过测点，因此液面高度随时间变化在15～20s区段内应呈现出“升高—回落—再升高”的特点。由图2可见，当粒子间距dp设置为0.15m时由于粒子数量过少，模拟精度差，无法体现这一过程，而当粒子间据dp设置为0.12m和0.10m时虽然能较好地模拟液面的复杂变化，但由于粒子数量较少，数据沿程频繁发生发生突变。若将粒子间距dp设置为0.08m则可以很好地解决这一问题，不仅能够准确地模拟海啸波传播过程中的变化特点，还模拟出60s的传播过程在计算机上运行时间需要8h左右，计算效率和精度均得到保证。为检验数值模拟方法的准确性，将波高6m，不设置其他地形的条件下在200m处测得的波面变化数据与孤立波理论波形相对比：结果如图3所示，理论值与数值模拟结果吻合良好，表明本文数值模型结果可靠。

图2 不同粒子间距自由液面高度随时间的变化Fig.2 Time-dependent variation of free surface height at different particles spacing

图3 理论值与数值模拟波形对比Fig.3 Comparison of theoretical values and numerical simulation

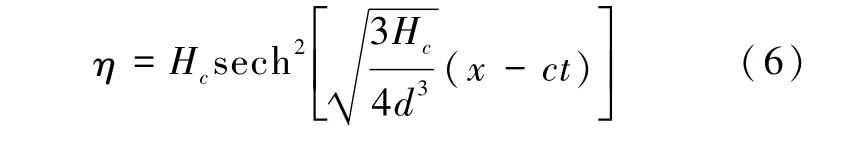
2.2 粒子分辨率对作用力的影响

通过计算10m高墙体上一侧静水压力大小来分析粒子间距对作用力的影响［9］。理论静水压力为490500N.如图4所示，作用力振荡随着时间推移逐渐减小，粒子分辨率dp＝0.08m的算例振荡显著小于粒子间距较大的另外两组。3个算例最后 20 组数据的平均值分别为492654N、498280N、476103N，与理论值的误差分别为0.44%、1.59%、2.94%。因此当粒子采用较小间距时，能够降低作用力测量的误差，综合考虑数值模拟精度和计算效率，本文均采用粒子间距dp＝0.08m进行模拟。

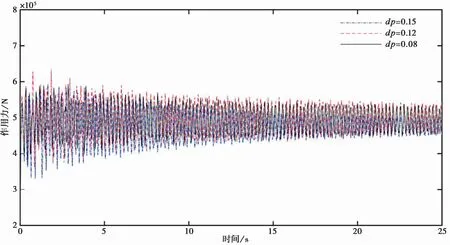
图4 三种不同粒子间距下的作用力振荡Fig.4 The vibration of forces with three kinds of particle spacing

3 孤立波在不同地形珊瑚礁上的传播与演变

基本的模型设置参数见表1，工况1至工况5设置了5组不同礁前斜坡坡度，研究坡度对孤立波在斜坡上传播、演化、破碎以及波能耗散的影响。工况6则在斜坡上部设置一护岸结构，并与工况4对比研究护岸结构与孤立波间的相互作用。工况7与工况8通过在礁坪上放置建筑物，在瀉湖内放置浮体来研究海啸波对岛礁建筑和停泊船只的危害。

表1 各组工况参数设置Tab.1 Setting of operating conditions

3.1 礁前斜坡坡度对孤立波传播变形的影响

在保持珊瑚礁礁坪高程与静水面平齐的情况下，建立了5组不同礁前坡度的算例以探究礁前坡度对海啸波在环礁地形上传播的影响。

根据合田良实波浪破碎指标［10］：

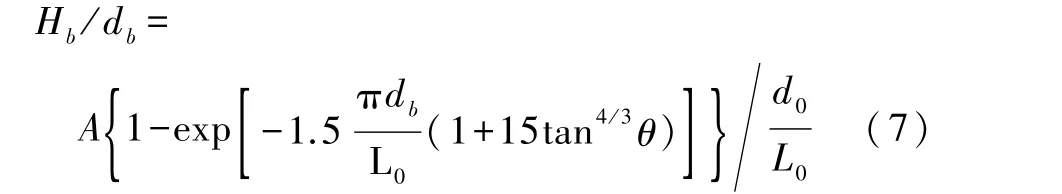
可知不同礁前坡度下孤立波均在水深约2.2m处破碎。

孤立波在向海坡段前传播过程中存在能量的耗散，在坡脚处波高衰减为5.86m，当波浪刚进入向海坡段时，波形尚未发生明显变化。随着水深逐渐减小，波形的不对称度显著增大，孤立波的前缘逐渐变陡峭，后部波面趋于平坦，直至280m附近，孤立波以卷破波的形式发生破碎，波高急剧下降。根据图5中不同坡度不同测点液面高程随时间变化可以看出，每个测点的液面高程数据均会出现多个较明显波峰，其中首个波峰对应入射波，其后数个对应反射波。反射波在向深水传播的过程中色散性逐渐体现，出现一系列波高较小的短波，由于反射波在造波板上二次反射末尾段水面再度出现较大的抬升。在入射波高相同的情况下通过对比反射波波高即可估计出不同坡度下波能的反射情况。1∶4坡度的首个反射波波高比为1∶8和1∶12的坡度分别高0.15m、0.32m，反射波波高随着坡度的增大而增大，波能反射率亦随之增大。图5a还能观察到反射波存在较明显的包络现象，即不同时刻的反射波在25～40s存在重叠，推测是由于陡峭的斜坡水深变化剧烈，色散性未充分体现，不同波长的反射波未完全分开。当坡度减小时，包络现象越来越不明显，各反射波相互之间独立性较好。

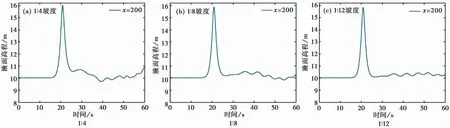
图5 不同坡度下自由液面高随时间变化图Fig.5 Time-dependent variation of the height of free surface under differ ent slopes

坡度对孤立波在礁前斜坡上传播时的波高变化有影响，当坡度较陡时，孤立波以激破波的形式破碎。如1∶4坡度工况下孤立波传播到岛礁附近并发生浅化变形，波峰逐渐变得尖陡，波高在200m 的坡脚处显著增大，随后在204～232m维持在较高位并缓慢下降。随着水深不断变浅，孤立波受到底部摩阻影响在234m处周围发生破碎，随后波浪涌上礁坪并迅速崩塌，波前水质点速度增至25m／s，相较于波峰刚传至坡脚处增幅达264%。当坡度为1∶6～1∶10时，孤立波的破碎形式由激破波向卷破波过渡，随着坡度趋缓，孤立波在斜坡上传播时间增加，非线性特征得到充分发展，波高最大值出现位置后移。由坡度为1∶12的波面最大高度随位置变化图可见，在240～286m处波高激增，在286～292m之间波浪发生破碎，约在286m处破碎前波高达极大值6.22m，破碎后在292～314m 间波高骤降37%。

因此当坡度较陡时，孤立波在刚进入礁前斜坡段波高便快速增长并出现最大值，随着坡度逐渐平缓，最大波高出现位置后移且波高度较1∶4坡度时逐渐下降，1∶8坡度下最大波高较1∶4坡度下降0.18m。当坡度进一步趋缓时，最大波高出现位置继续后移，但波高度则由于孤立波浅水非线性特征的充分发展而有所回升，1∶12坡度的最大波高相较1∶8坡度增加了0.32m。

潟湖内的波高与礁前斜坡坡度的相关关系与孤立波最大波高和坡度的关系相似，1∶6坡度条件下潟湖内波高分别比1∶8、1∶10坡度高34%和54%。但随着传播距离的增加均先剧烈衰减而后趋于稳定。

3.2 护岸对海啸波的防护效果

图6 不同坡度下最大波高沿程变化Fig.6 The maximum height of wave surface variations with different slopes

为探究在环礁地形上建设护岸结构对海啸波传播的影响，选取工况4与工况6对比试验，工况6相比于工况4在礁前斜坡段250m以后添置了护岸结构，护岸结构由宽3m的阶地，坡度为1∶2.5的光面斜坡及高为2m的胸墙三部分组成。护岸从底部起沿斜坡每隔10m布置了多个波压力测点，胸墙沿高度每隔0.5m布设测点以讨论护岸结构物在海啸波冲击下的安全性。礁前斜坡、礁坪、潟湖沿程布置一定数量的波高测点以研究护岸结构物对海啸波的防护效果。最大波浪力出现在护岸胸墙处，达到1612.5kPa，而护坡上最大波浪力也达到906kPa这一数据远大于岛礁护坡与胸墙推荐采用的设计标准值［11］，因此在海啸波的冲击下一般的护岸结构破坏几乎是必然的，若岛礁上有重要设施要保护，应考虑在胸墙前布置护面块体来耗散水流的冲击力或提高护岸结构的设计参数。

从两算例中选取了200m和320m处的4个测点的数据来研究护岸结构物对海啸波的防护效果。如图9所示，该点避开了孤立波撞击胸墙后飞溅的水体。前文已对200m处的波高情况进行过分析，此处不再赘述。随着水流在礁坪上的传播，37.10s后，测点处仅剩一层流体粒子向潟湖方向运动，有时该测点处甚至没有水体，因此37.10s后数据尤为平直。

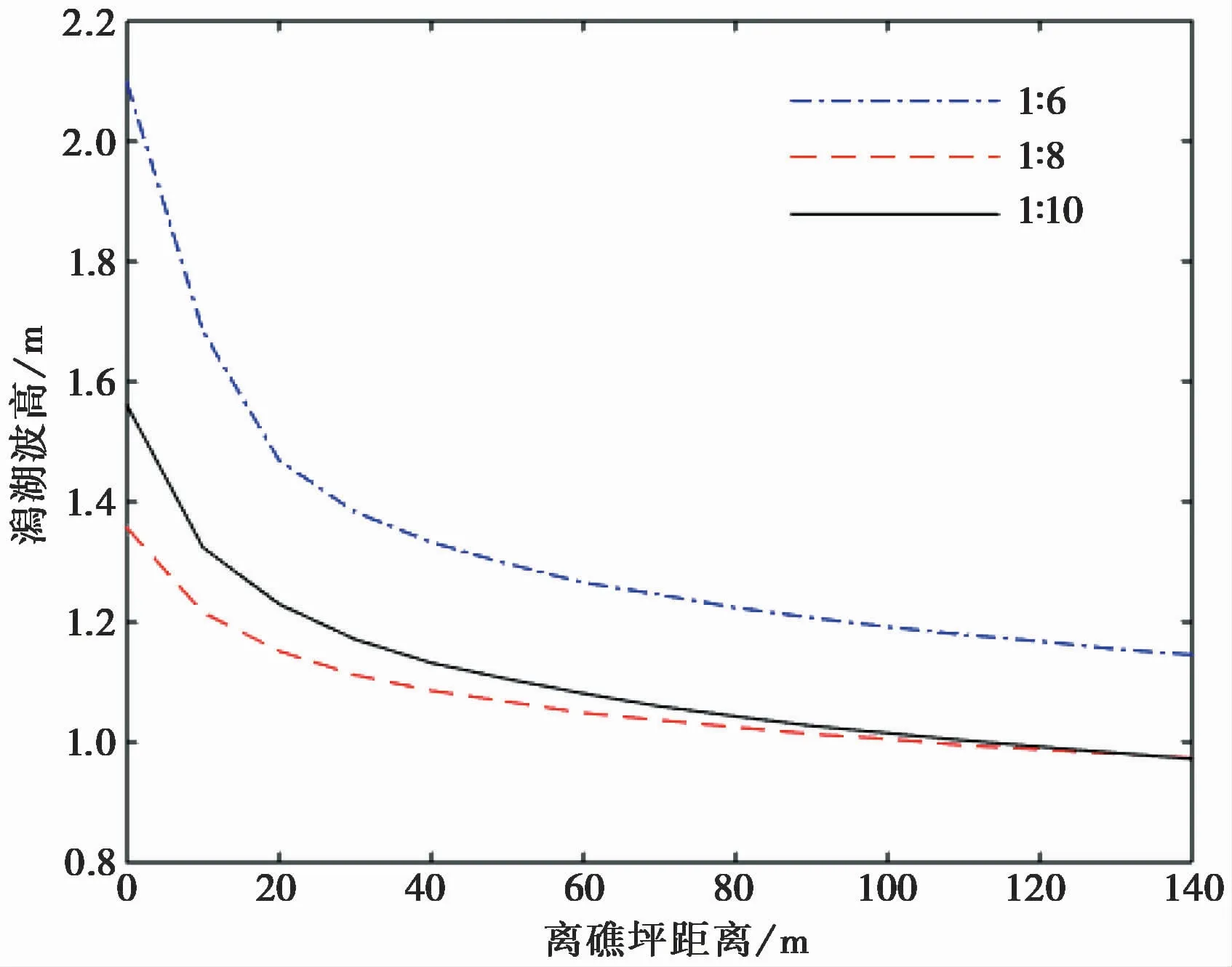
图7 潟湖内波高随礁前斜坡坡度的变化规律Fig.7 The variation of wave height in the lagoon with slope gradient in front of reef

图8 波浪与护岸结构相互作用及越浪过程Fig.8 The interaction between wave and r evetment structure and overtopping process

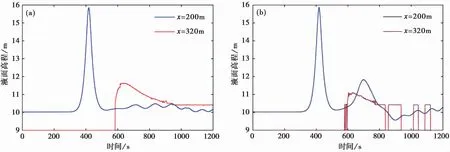
图9 无护岸（a）与有护岸（b）工况下x＝200m 与x＝320m 处液面高度Fig.9 Free surface level at x＝200m and x＝320m with（a）or without revetment（b）

两组数据存在几个明显的不同点：一是有护岸情况下反射波波高显著大于无护岸，最大反射波波高可以达到入射波高的36.16%，而无护岸时仅为13.98%，因此胸墙的存在能够提高波浪的反射率。二是礁坪上波高显著减小，有护岸时礁坪上的最大波高比无护岸情况减小0.527m。

3.3 海啸波对建筑物的荷载

假设在400m处的礁坪上有一高为8m，长度10m的两层楼建筑物。

在建筑物迎浪方向沿高每隔0.5m 设置波压力测点，并计算整个建筑物所受到的x方向与z方向作用力。无护岸时建筑物迎浪方向压强分布如图10所示，最大瞬时局部力出现在建筑物底部，超过2900k N／m2，建筑物整体受力也达到399.6kN／m2。民用工程大多难以承受如此大的荷载，因此对于常受海啸影响的有建筑岛礁，应设置如护岸、防波堤等防护措施。设置护岸后由于越浪量降低，建筑物中部2m 高处受力也从769.2k N／m2减小至241.2kN／m2，同时整体受力也减小到286.2kN／m，减小了28.4%，建筑物的稳定性相应提升，但底部仍受礁坪上传播的高速水流冲击，虽然最大局部力减小了48.7%，局部瞬时荷载仍达到了1500kN／m2，因此可以考虑对建筑物底部进行加固或者在礁坪上沿程布设多级消力坎等补充防护措施，考虑到不影响岛礁上人员正常生活，消力坎高度建议设置为0.5～1m。

图10 最大波压力沿建筑物高度的分布Fig.10 The distribution of maximum wave pressures along the height of the building

3.4 孤立波对潟湖的影响及停泊船只安全分析

选取1∶10坡度的算例来研究孤立波经一系列能量损失后对潟湖的影响，采用1m波高作为停泊安全的评判标准［12］。潟湖内自500m开始间隔10m布置一系列波高测点，同时浮体设置在距离礁坪50、100、150m 以研究停泊点离礁坪的距离对船只停泊安全的影响，三个停泊处水深始终为10m，以保证现实中船舶停泊拥有较好的水深条件，不会搁浅。测得结果见表2，3个测点的最大波高及浮体受力的衰减均在34%以上，因此护岸能显著的降低潟湖内的波高以及靠近礁坪处浮体的受力，同时最大横摇角度也降低30%以上，表明护岸很好的改善了船舶的泊稳条件。受限于计算能力，本文中200m的礁坪宽度在实际环礁地形中属于偏小的一类，在此条件下即使有护岸靠岸停泊的波高和侧向波浪力仍过大，而离岸停泊对波高、浮体受力和船舶横摇的削减幅度最大达到了96.8%、65.2%以及90.2%，所以对于较小的环礁离岸停泊更为安全。

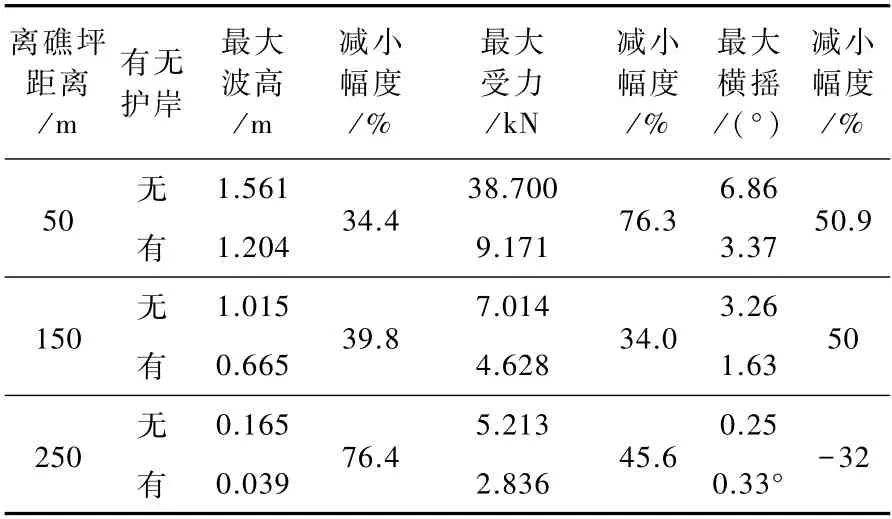
表2 实验各工况波浪要素Tab.2 Wave elements in various operating conditions

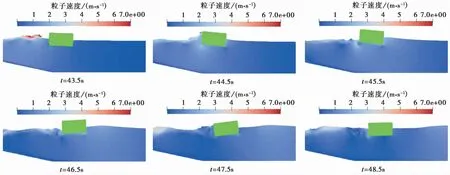
图11 波浪作用下浮体的运动过程Fig.11 The movement process of floating under the action of wave

4 结论

本文针对孤立波与环礁地形的相互作用进行了数值模拟，分析了孤立波在环礁地形上的传播演化特征以及岛礁建筑物与停泊船只上荷载随时间的变化规律，得出了以下结论：

（1）礁前斜坡坡度越大，波能反射率越高，但其浅水非线性特征得不到充分发展，礁坪前缘波高反而更大。

（2）潟湖内的波高受到礁前斜坡坡度以及波浪破碎形式的影响，破碎形式为滚破波时波高最小，卷破波和激破波则较大。

（3）近岸波高为6m的海啸波对护岸胸墙处作用力最大达到1600kPa，对护面部分也能达到900kPa，能够破坏一般的护岸结构，应考虑多种措施如放置护面块体共同使用来防灾减灾。

（4）护岸能有效降低礁坪上建筑物整体所受荷载，但即使设置护岸建筑物底部最大荷载仍能达到1500kN／m2，因此最好在建筑物前设置一些措施如消力坎来应对高速水流。

（5）护岸能降低潟湖内波浪和船只所受侧向波浪力，但最好将船只停靠在来波方向对岸，留足水域供波浪消能。