结构抗侧刚度计算方法的研究现状与进展

董 策，郭 迅，齐芳月，王 超，唐小宝

（1.防灾科技学院，河北 三河 065201；2.中国地震局建筑物破坏机理与防御重点实验室，河北 三河 065201）

0 引言

我国地域辽阔，地处欧亚地震带和环太平洋地震带之间，受太平洋板块、印度洋板块的挤压影响，使得我国地震频繁发生且分布广，其造成的次生灾害也非常严重［1］。如1976年唐山7.6级地震、2008年汶川8.0级地震等大地震都造成了重大的人员伤亡和财产损失［2］。

地震引起的建筑结构倒塌是造成人员伤亡的主要原因［3］，因此建筑结构抗震研究是非常重要的研究方向。基于实际震害，国内外专家学者在建筑抗震方面的研究取得了大量的成果，如国内颁布并实施的《建筑结构抗震设计规范》等。在对高度不超过40m的多层框架结构或多层砌体结构进行抗震设计时，一般采用底部剪力法计算水平地震剪力，其中层间水平地震剪力是按照墙段层间等效抗侧移刚度（以下简称“抗侧刚度”）进行分配的，所以要算地震剪力的分配，首先要计算出纵横轴各墙体的抗侧刚度。在地震作用下，建筑结构中设置不均匀的构件抗侧刚度越大，分配得到的水平地震剪力就越大，此构件就容易率先发生破坏，进而导致结构整体破坏，即所谓的“凝震聚力，个个击破”［4］，因此抗侧刚度是建筑抗震设计中一个非常重要的参数。

从近些年国内外学者对结构抗侧刚度的研究来看，不考虑圈梁构造柱的砌体结构抗侧刚度计算方法的研究成果较为完善，而对考虑构造柱的砌体抗侧刚度研究尚有不足。对RC框架结构抗侧刚度的研究较多，发表了不少的成果。本文基于这些成果理论主要从砌体结构和RC框架结构抗侧刚度在弹性阶段内的理论计算加以总结分析。

1 砌体结构抗侧刚度计算方法

1.1 无洞墙段抗侧刚度计算

对于不考虑圈梁、构造柱影响的不开洞砌体墙段在计算其抗侧刚度时，根据力学知识一般假定墙段的上端为嵌固约束，下端为固定约束（图1），在水平推力作用下墙段顶端产生的侧向位移的倒数即为墙段的抗侧刚度［5，6］。在计算墙段抗侧刚度时要依据墙段的高宽比综合考虑剪切和弯曲变形的影响。

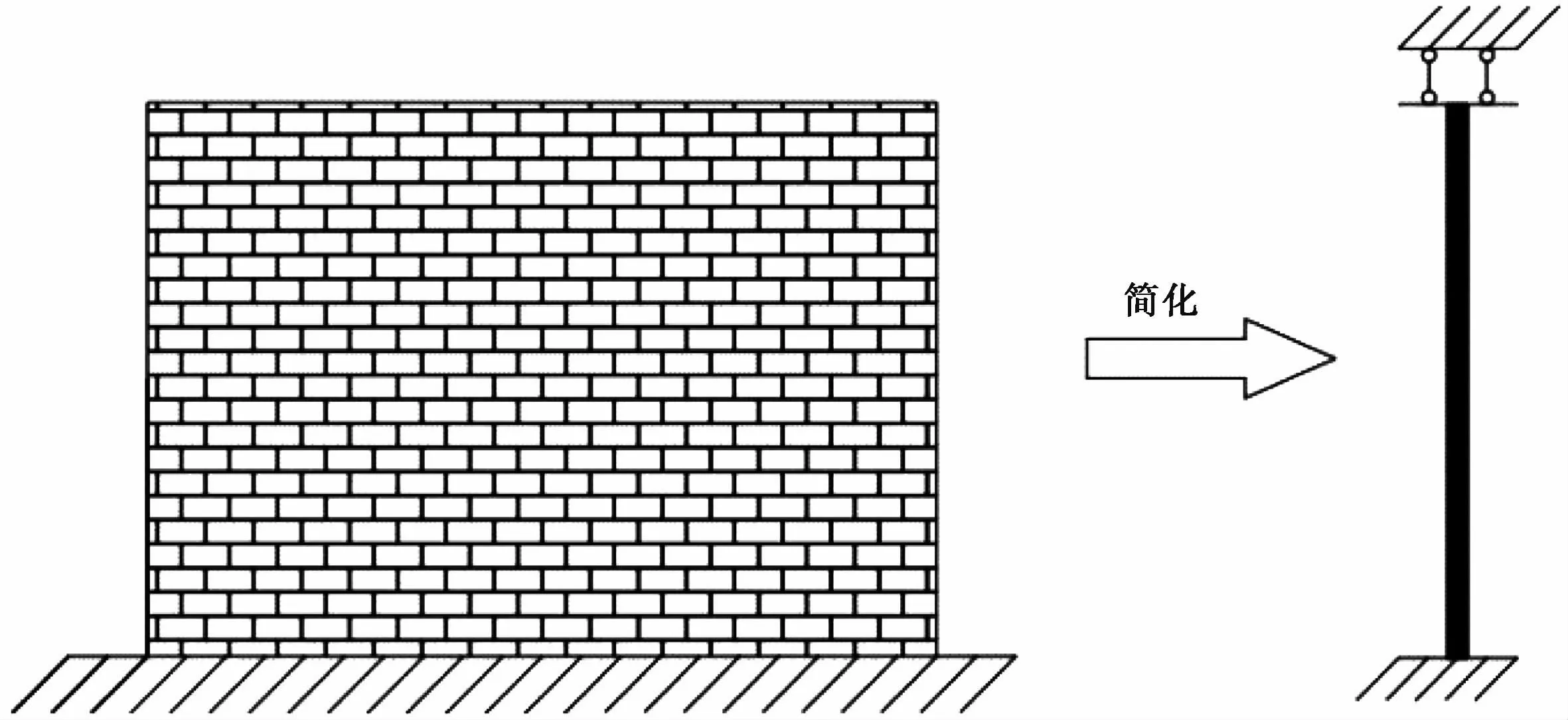
图1 墙片简化图Fig.1 Simplifiedwallsheet

剪切侧移：

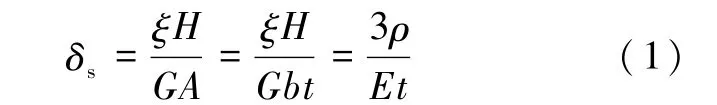
弯曲侧移：

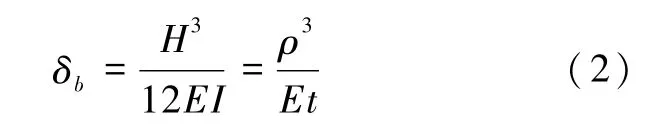
式中：H、B、t为墙段的高度、宽度和厚度；E为砌体墙的弹性模量；G为剪切模量，根据材料泊松比一般取G＝0.4E；ξ为剪切变形截面系数，矩形截面取1.2；ρ为墙段的高宽比，即ρ＝H／B。

依据 《建筑结构抗震设计规范》（GB50011－2010）（以下简称《抗震规范》）［7］中对高宽比的规定有：

①ρ＜1时，仅考虑剪切变形的影响，即抗侧刚度

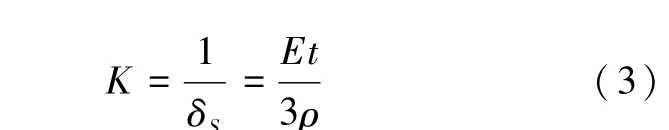
②1≤ρ≤4时，需同时考虑剪切和弯曲变形的影响，即

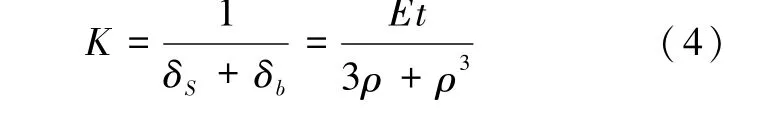
③ρ＞4时，以弯曲变形影响为主，可不考虑抗侧刚度。

以上为弹性阶段不考虑圈梁、构造柱影响时砌体结构墙段抗侧刚度理论计算方法，在诸多文献中都已给出［5.6，8，9］。通过对唐山地震、汶川地震等数次地震的震害调查研究发现，圈梁、构造柱的合理设置能显著提高结构的抗震能力，表明构造柱对结构抗侧刚度的贡献是非常大的，显然上述抗侧刚度计算方法是不完善的。现行《抗震规范》中的第7.1.8条也指出计算底层框架或底部两层框架－抗震墙砌体建筑房屋纵横向抗侧刚度时，上部砌体部分中的构造柱要参与计算考虑其影响，所以抗侧刚度的计算方法应加以改进［7］。

《设置钢筋混凝土构造柱多层砖房技术规程》（TDT／T13—94）［10］（以下简称《规程》）中详细规定了砖混结构对构造柱的设置及抗侧刚度的计算等。此规程中墙体抗侧刚度的计算方法在式（4）的基础上做了细化处理，同时考虑了构造柱、开洞及剪弯作用的影响，《规程》中采用了折算法考虑构造柱的作用，其公式如下：

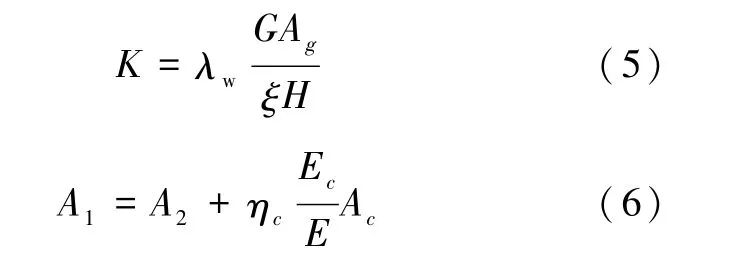
式中：A1为墙段折算后的水平截面面积；A2为墙段扣除孔洞及构造柱截面积后的砖砌体水平截面净面积；Ac为构造柱截面面积；ηc为构造柱参与墙体工作系数，H／B≥0.5时，取0.30；H／B＜0.5时，取0.26；Ec为混凝土的弹性模量；Ag为墙段水平截面的毛面积；λw为考虑墙段孔洞和弯曲变形的刚度修正系数。

此种计算方法虽然考虑了构造柱对结构抗侧刚度的贡献，但其中构造柱参与墙体工作系数并未考虑构造柱位置设置带来的影响。如果工作系数取值过大会导致墙体受力计算时墙体分配到的剪力过大，造成的误差也相应增大［11］，所以此公式工作系数取值需进一步改进。

刘红彪、周洋 等［11，12］通 过 对 设 置 圈 梁、构 造柱的砌体墙片进行有限元分析及拟静力实验验证，研究了圈梁以及构造柱设置位置对墙片抗侧刚度的影响，并对《规程》中计算方法进行了完善。结果表明不同高度的圈梁对墙片刚度的影响并不大，计算抗侧刚度时可忽略其影响。同时结合式（4）和式（6）给出了具体构造柱参与工作系数的取值，进行刚度计算时取ρ＝Ht／A1。即

1.2 开洞墙段抗侧刚度计算

国内外关于开洞墙段抗侧刚度不同的计算方法中约束条件也不尽相同，本文对此进行了总结分析。

Tri-ServiceManual法［13－15］将开洞墙体的侧向位移分成三部分进行计算，如图2所示。首先计算与整片墙体等面积的实体墙的抗侧向位移Δw，其次计算与开洞墙带部分等面积的实体墙的抗侧向位移Δs，然后计算洞口两侧小墙体部分的抗侧向位移Δp，最后计算整片开洞墙体的总侧向位移Δ＝Δw－Δs＋Δp，进而得到墙体的抗侧刚度即K＝1／Δ。此方法的局限性在于只适用于一或两层的开口墙体抗侧刚度的简化计算，其计算结果与实际相比误差大。

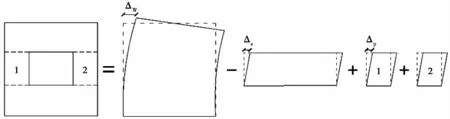
图2 刚度计算示意图Fig.2 Schematicdiagram ofstiffnesscalculation

Tri-ServiceManual法计算抗侧刚度时要考虑墙体端部约束对变形的影响，针对此Brandow等［15，16］研究指出开洞形成的墙带以及洞口两侧划分的墙体应予以假定为上下端固定约束（图3），实体墙端部约束应假定为底部固结、顶端嵌固（图1），各部分宜按相应的方法计算侧向位移。而Lindeburg和Baradar［17］指出开洞墙体划分后各部分端部约束均应假定为下端固定、上端嵌固，在此条件下考虑变形影响并进一步计算墙体的抗侧刚度。假定的约束条件不同，由此计算的抗侧刚度也随之不同。

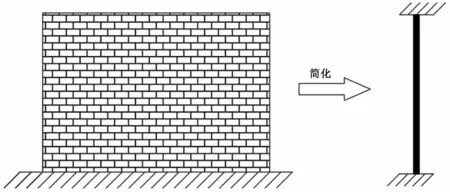
图3 墙体等效图Fig.3 Wallequivalentdiagram

Benjamin和Williams法［18，19］研究指出对于开洞墙体仅计算洞口两侧墙肢部分（图4中②和③部分）的抗侧刚度即可，上下墙带的位移变形较小对整片墙抗侧刚度的影响可忽略。此法计算简单，但墙体的总刚度往往会被高估。

图4 开洞墙体划分图Fig.4 Openingwalldivisiondiagram

Dickey和Schneider法［20］则强调洞口两侧墙肢及上下端墙带的侧向位移变形都需要考虑，此法在计算时应考虑两种约束的不同：当墙体顶端约束较小可忽略或无约束时，墙肢应视为悬臂梁，反之视为滑动铰支座。

Qamaruddin法［21－23］与Benjamin法相似，但其关于墙体顶端约束的假定却不相同，依据开口情况考虑洞口上下方墙带尺寸的影响，采用部分固结条件计算［20］。该方法的精确性相比其他方法有所提高，但不适用于以剪切破坏为主的抗侧刚度计算。

Balasubramanian法等［24－27］对开口墙体据不同的边缘约束条件划分并计算各部分刚度，然后叠加组合总体刚度。该方法全面考虑了门窗洞口出裂缝开展趋势对弯曲变形的影响，对砌体结构计算结果的准确性有所提高，但其计算过程相当复杂不符合实用条件。

现行《抗震规范》中开洞率对墙段抗侧刚度的影响有明确的规定，即墙段宜按照门窗洞口进行划分，依据开洞率的大小将墙片划分为小开口墙和大开口墙，对设置构造柱的小开口墙段按毛墙面的抗侧刚度乘以洞口影响系数进行计算［7］。该方法计算结果与实际抗侧刚度结果相差偏大，存在一定的不合理之处，需要改善优化。

刘红彪、周洋等［11－12］对开洞墙体的抗侧刚度进行了深入研究。指出计算开口砌体墙片的抗侧刚度仍按照上述无洞墙体抗侧刚度的计算公式进行，同时通过对开洞墙体进行拟静力试验和有限元分析，结合前人研究成果确定了墙体依据洞口位置划分为若干墙肢，逐个计算刚度，最后利用刚度串并联法整合出开洞墙体的总刚度，见式（7）。与《抗震规范》相比该方法避免了对墙体开洞率的考虑，并将构造柱的影响考虑了进去，划分原则如图5所示。该法与上述方法相比不同之处在于计算总的抗侧刚度时考虑了墙体各部分串并联的关系，在一定程度上提高了计算结果的准确性。

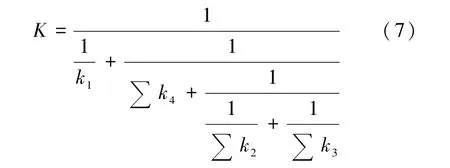
式中：k1、k2、k3、k4分 别 指 图5中①、②、③和④各部分的墙段抗侧刚度之和。

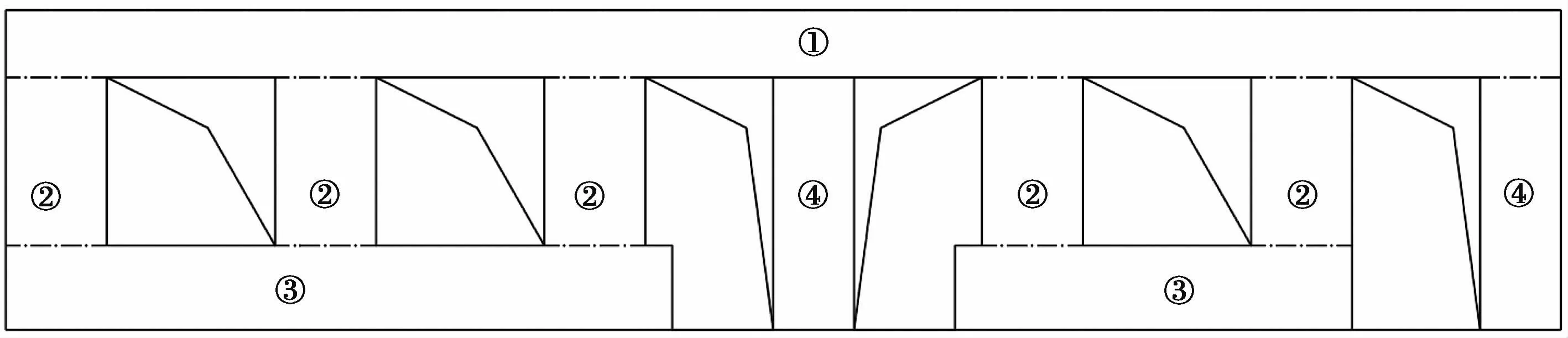
图5 带洞墙片划分原则Fig.5 Principleofdividingwallwithholes

2 RC框架结构抗侧刚度计算方法

钢筋混凝土框架结构中柱的抗侧刚度与梁的线刚度有关，在现行规范中常用D值法求解RC框架的刚度［8］。依据结构力学［28］考虑柱的反弯点高度受上下层梁线刚度比、层高变化等因素有关，对以D表示柱的抗侧刚度进行修正，即为D值法。公式表示为：

式中：Dij为第i层第j根柱的抗侧刚度；iz为框架柱线刚度；h为框架柱高度；α为柱上下端节点弹性约束的修正系数。

RC框架结构中的填充墙在工程设计时一般被认为是非结构构件，然而数次地震的实际震害显示，实心砌体砖填充墙的存在以及布置方式大大地影响了框架结构的抗震性能［29－32］，对框架结构的破坏“功不可没”［33］。因此填充墙这一影响因素受到了国内外专家学者的重视并进行了大量的研究，得到了许多的结论［34－36］，在计算带填充墙的RC框架抗侧刚度时应把填充墙的影响考虑进去。

《建筑抗震设计规范》（GBJ11－89）［37］（以下简称《89规范》）中给出了填充墙框架的抗侧刚度计算的公式：

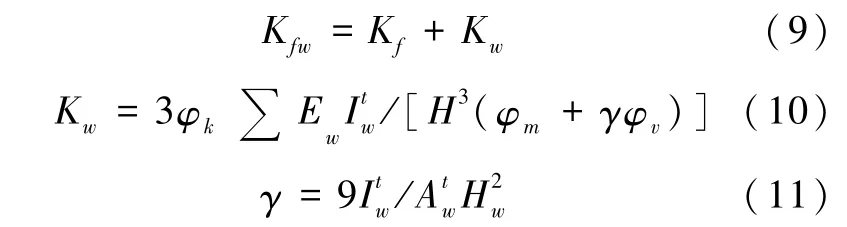
式中：Kf为框架柱的总抗侧刚度；Kw为填充墙的抗侧刚度；Aw为填充墙水平截面积；Hw为填充墙高度；Ew为砌体填充墙弹性模量；φk为侧移刚度折减系数；γ为剪切影响系数；φm、φv为洞口影响系数，无洞口时取1。

《89规范》给出的层间抗侧刚度计算公式，考虑了实心砖砌体填充墙对框架结构刚度的贡献，同时考虑了层间变化和开洞带的影响，分别通过层数三等分及洞口位置给出了刚度折减系数的取值和洞口影响系数的计算公式。此法对于洞口率大于60%的填充墙不予考虑，虽然考虑的影响因素比较全面但是在实际计算中存在一定的误差。2001修订版《抗震设计规范》规定地震作用下的层间剪力与层间位移的比值即为楼层的侧向刚度，而现行10版《抗震规范》修订后删除了《89规范》给出的填充墙框架的抗侧刚度计算公式及01版的规定。

黄华等［38］通过有限元软件对一个10层的填充墙框架结构进行了模拟分析，其中填充墙采用的是shell63单元，填充墙和框架之间采用了半刚性连接。该模拟结果结合《抗震规范》和《规程》假定条件给出了层间抗侧刚度的计算式（12），并确定了填充墙抗侧刚度折减系数βw取值为0.25。此法仅依据有限元模拟给出了相应的结论，没有结合实际实验加以验证，通过此公式算得的结果误差大并不实用。

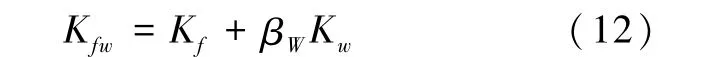
吴绮云等［39］将砌体填充墙及钢筋混凝土框架看作成整体的组合板结构，在单向反复水平推力的作用下研究了组合结构的受力破坏过程，并分析了其变形和破坏的特点，最后给出了线弹性阶段抗侧刚度的计算公式：

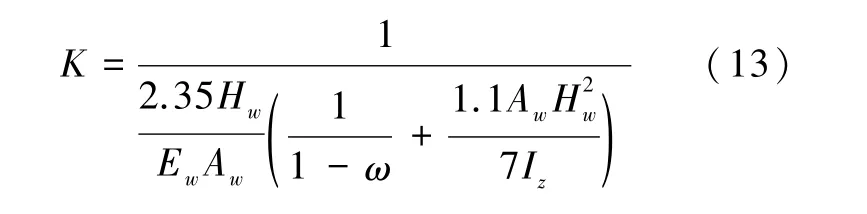
式中：ω为开洞影响系数；Iz为整体组合板的惯性矩。

童岳生等［40－41］在水平反复荷载的作用下对多榀一层单跨的砖砌填充墙框架进行了试验研究，对取得的力－位移曲线深入分析后采用填充墙刚度和框架刚度相叠加的方式，提出了较为实用的三折线刚度计算法，并给出了线性阶段的抗侧刚度计算公式：

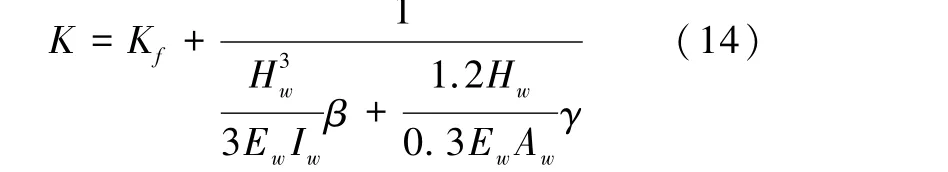
式中：β、γ为开洞影响系数。

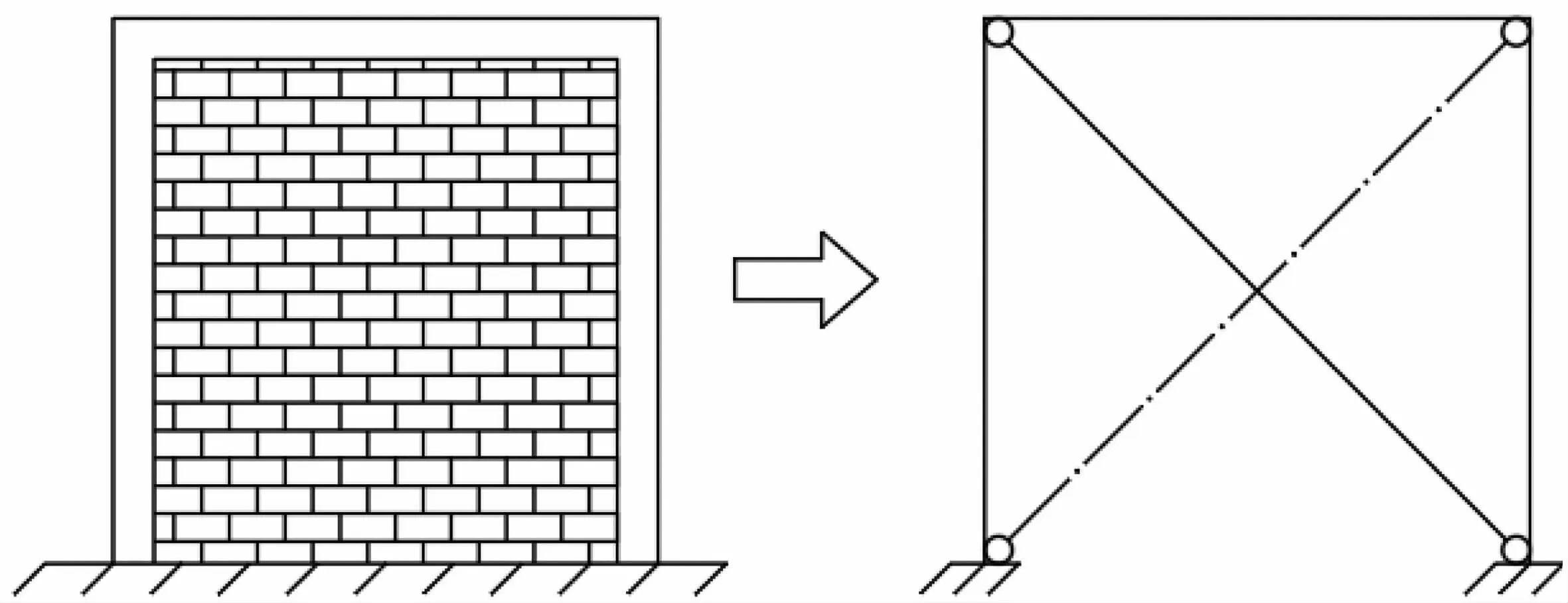
图6 等效斜压杆模型简化图Fig.6 Simplifieddiagram ofequivalentobliquestrutmodel

关国雄等［42］对一个1∶3的四层砖砌填充墙RC框架结构模型进行了振动台试验，将砖砌体填充墙和钢筋混凝土框架近似地看做成整体结构，考虑了填充墙的变形模量降低因子等，结合实验结果和结构动力性能分析，提出了层间抗侧刚度的计算公式：

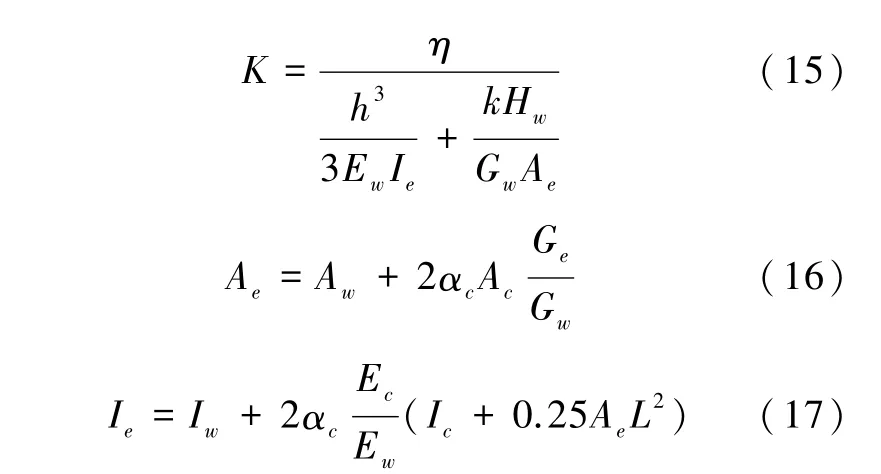
式中：η为填充墙的变形模量降低因子，弹性阶段取η＝1；h为钢筋混凝土框架高度；k为填充墙的剪切贡献系数；L为框架的跨度；αc为抗侧刚度的影响系数，墙与框架接触好时取1。

以上对带填充墙钢筋混凝土框架抗侧刚度的研究方法和计算公式是基于结构力学知识考虑剪弯变形直接通过实验、有限元模拟及理论分析得到的，其计算值与实测值相比存在一定的误差。除以上研究方法外，国内外学者采用等效斜压杆模型计算抗侧刚度的研究方法较为普遍。Polyajcov［43］指出把填充墙视作为一个只承受压力作用的与RC框架相连的斜压支撑杆即为等效斜压杆模型如图2所示。

乔墩等［44］通过对多种计算方法的比较，选取了等效斜压杆模型计算整体结构的抗侧刚度，给出了抗侧刚度的计算式（18）。并且发现等效斜压杆模型中斜压杆宽度ω的取值是关键，国内外学者对压杆宽度进行了各种研究，如Simth等［45］通过给出一个特征参数λ来表征压杆宽度对钢筋混凝土框架及砖砌填充墙刚度的影响；Papia等［46］研究指出压杆宽度还与框架柱的变形有着紧密的联系，给出了一个计算过程相当复杂的公式等。通过对比分析，乔墩给出的计算公式中最终采用了MSTC［47］提供的压杆宽度计算式（18），由此得到的抗侧刚度计算结果较为准确。

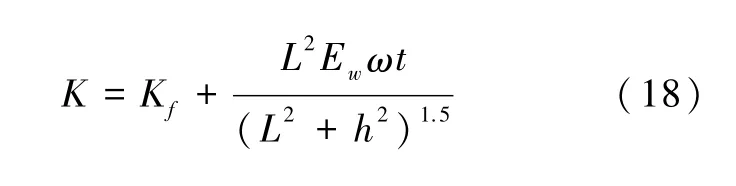
此外，对带填充墙的框架结构弹性抗侧刚度计算方法的研究，不管是直接考虑剪切和弯曲变形给出的计算公式，还是采用等效斜压杆模型考虑压杆宽度等因素给出的计算公式，对于开洞的影响很少进行深入的分析。国内外实际震害显示，洞口设置会改变填充墙的刚度和强度，甚至改变整体结构的受力机制，使结构破坏加重。孔璟常等［48］通过对开洞填充墙的框架结构进行实验和有限元模拟分析，考虑了洞口大小、高宽比、开口形式及设置位置等影响因素，基于等效斜压杆简化模型，提出了开洞填充墙的刚度折减系数，给出了相应的计算公式等，但对于开洞填充墙的RC框架结构还需进一步研究。

3 结论与讨论

国内外学者不断通过实验和有限元模拟对结构线弹性阶段的抗侧刚度计算方法进行研究，且取得了突出的理论成果。本文通过对以往的理论计算方法进行对比分析，并探讨了各种计算方法的优缺点，得到了以下结论：

（1）对于砌体结构，构造柱的存在大大地影响了结构的抗侧移刚度，而且对于考虑构造柱影响的抗侧刚度计算研究理论成果相对较少，仅有的考虑构造柱的计算方法计算值误差较大，有待进一步改进优化。同时是否开洞、洞口尺寸以及洞口所处位置等因素也是结构抗侧刚度计算的关键所在，现有的研究成果较少且存在不足之处。

（2）对于钢筋混凝土框架结构，一般采用D值法计算其抗侧刚度。填充墙的存在虽然在工程设计中不作为构件考虑，但其对RC结构的抗震性能影响是很大的，故在计算刚度时要把填充墙考虑进去。直接考虑填充墙剪切弯曲变形得到的计算值大概是实测值的1～10倍；利用等效斜压杆模型计算的刚度深受压杆宽度的影响，其次填充墙的布置方式、填充材料、是否开洞、洞口大小等因素也需要进一步研究。

不论是砌体结构还是框架结构，现有的结构抗侧刚度计算方法都存在一定欠缺，尚需进一步的深入研究和改进完善。全面考虑各种因素对结构抗侧刚度的影响，完善相应的计算理论，才能进一步优化抗震设计，为建筑抗震的韧性评价提供服务。