一种低轨卫星星座测控地面站调度策略研究

安元元，李伟超，王伟，杨旭海，韦沛，王霄

一种低轨卫星星座测控地面站调度策略研究

安元元1,2,3，李伟超1,2，王伟1,2，杨旭海1,2，韦沛1,2,3，王霄1,2

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3. 中国科学院大学，北京 100049）

随着不同用途低轨星座快速发展，低轨星座对地面站的需求越来越强烈。根据任务需求和约束，需要对低轨卫星测控地面站资源调度采取最优的策略。本论文主要针对特定的低轨卫星Walker星座，研究遥测、遥控及数据传递等测控任务的最优调度，调度的基本条件是优先观测亟待数据更新的卫星。根据上述测控原则，本文提出了两种调度策略：1.优先选择俯仰角高的卫星；2.优先选择可视弧段长的卫星。现有4个测控地面站，分别为：长春、喀什、昆明、西安，每站均为单天线(同时只能观测一颗卫星)，通过仿真，验证两种策略优势，结果表明：虽然两种策略都可实现对地面站的调度，但策略2可避免天线频繁切换操作，策略2在实际应用上优于策略1，更适合于实际卫星测控任务。

低轨卫星；遥测遥控地面站；资源调度；优化仿真

0 引言

以卫星运行高度划分，卫星可分为同步轨道卫星（geosynchronous earth orbit，GEO，35 786 km）、中轨卫星（medium earth orbit，MEO，8 000～20 000 km）和低轨卫星（low earth orbit，LEO，500～2 000 km）[1]，低轨卫星距离地面近，具有时延小，路径损耗小，发射功率小等优势，广泛应用于各个领域[2-3]。特别是近年来在卫星导航领域的应用，建立基于低轨卫星星座的通信与导航相融合的、全新的卫星导航系统已成为发展趋势。低轨卫星星座测控和精密定轨成为下一代GNSS（Global Navigation Satellite System）导航系统的关键技术之一受到广泛关注[4]。我国于20世纪初组建北斗卫星导航系统，2020年6月23日，北斗全球卫星导航系统完成卫星组网。仿真研究表明，加入低轨卫星星座后，下一代北斗导航系统地面测站可见卫星数显著增加，全球PDOP（position dilution of precision）值有明显提升，全球区域导航精度均有提升，其中美洲区域提升效果最为显著[5]。低轨卫星增强地面区域监测站测定北斗卫星导航系统，可以减少地面站监测站的布设数量，提高跟踪弧段，优化空间几何构型，提高定位精度，从而显著提升北斗导航系统的服务性能[6]。卫星测控指的是接收卫星上各种实时状况和信息、为卫星提供各种系统控制信息[7]。低轨卫星覆盖区域小，实现全球覆盖需要较多的卫星，因此低轨卫星星座测控凸显其复杂性、重要性[8-9]。表1列举了部分国家的低轨卫星星座及实现覆盖的卫星数。

表1 全球覆盖的星座计划

低轨卫星的测控调度既要确保卫星的遥控、数据传递任务圆满完成，又要使有限的地面站资源合理、最优的使用。不同低轨星座由于其星座构成、任务的不同，其地面站资源最优化调度策略存在很大的不同。随着低轨星座及卫星数量的不断增加，传统的人工调度地面站资源方式无法满足实际的测控需求，因此必须研究相关的策略、模型和算法，提升卫星地面站的使用效率，实现卫星测控地面站高效、自动化调度。

对低轨卫星测控的调度策略的研究颇多，T. D. Gooley[10-11]对低轨道卫星的调度建立了整数规划模型，J. C. Pemberton[12]建立了约束（constraint satisfaction problem，CSP）模型，考虑了3类约束：资源约束、任务约束和时间约束。金光等[13-14]建立了Petri网卫星调度模型，还有学者研究建立了Agent模型，S. E. Burrowbridge[15-16]通过贪婪算法实现一个地面站对多颗低轨卫星的调度方案，贺成杰等[17]发现禁忌搜索算法优于列生成算法，W. J. Wolfe[18]发现遗传算法优于贪婪算法，王军民等[19]提出了基于卫星调度规则的启发算法。基于已有的模型和算法，已经产生了大量的、有价值的研究成果。本文结合我国不具备全球布站的不利条件，给出特定卫星星座的卫星测控相适应调度策略、模型和算法的最佳调度方案。

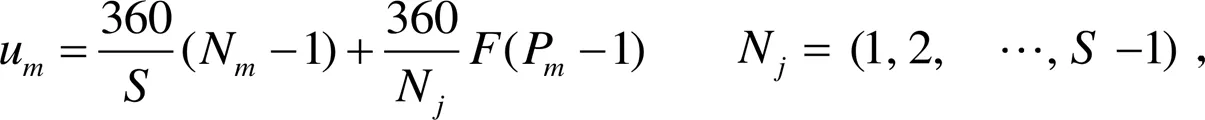
本论文涉及4个单天线地面站，分别为长春、喀什、昆明和西安。基于上述特定星座和现有的地面站，研究最优测控调度策略，使设计的策略既满足测控需求，又能使地面站资源使用优化。

地面站调度的约束条件如下：

① 由于卫星本身存储空间有限，每天必须下载其状态信息，确保每颗卫星每天至少观测20 min；

② 为保证每颗星被均匀观测，因此需要优先观测次数少的卫星；

③ 考虑尽可能少地切换卫星操作。

1 调度方案与策略

1.1 低轨卫星星座的覆盖特征

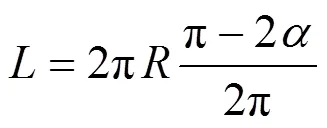
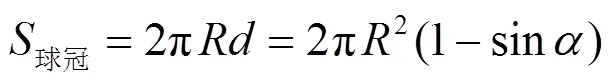
图1 卫星与地面站的几何关系

根据上面公式，不同高度的卫星覆盖情况见表2，本文研究的卫星高度为975 km，运行周期约1.8 h，覆盖弧长是6 657 km，覆盖面积是3.402×107km2，覆盖率为6.6%，因此覆盖全球至少需16颗卫星，对于卫星导航系统，要同时观测多于4颗卫星，全球覆盖至少需64颗以上卫星。

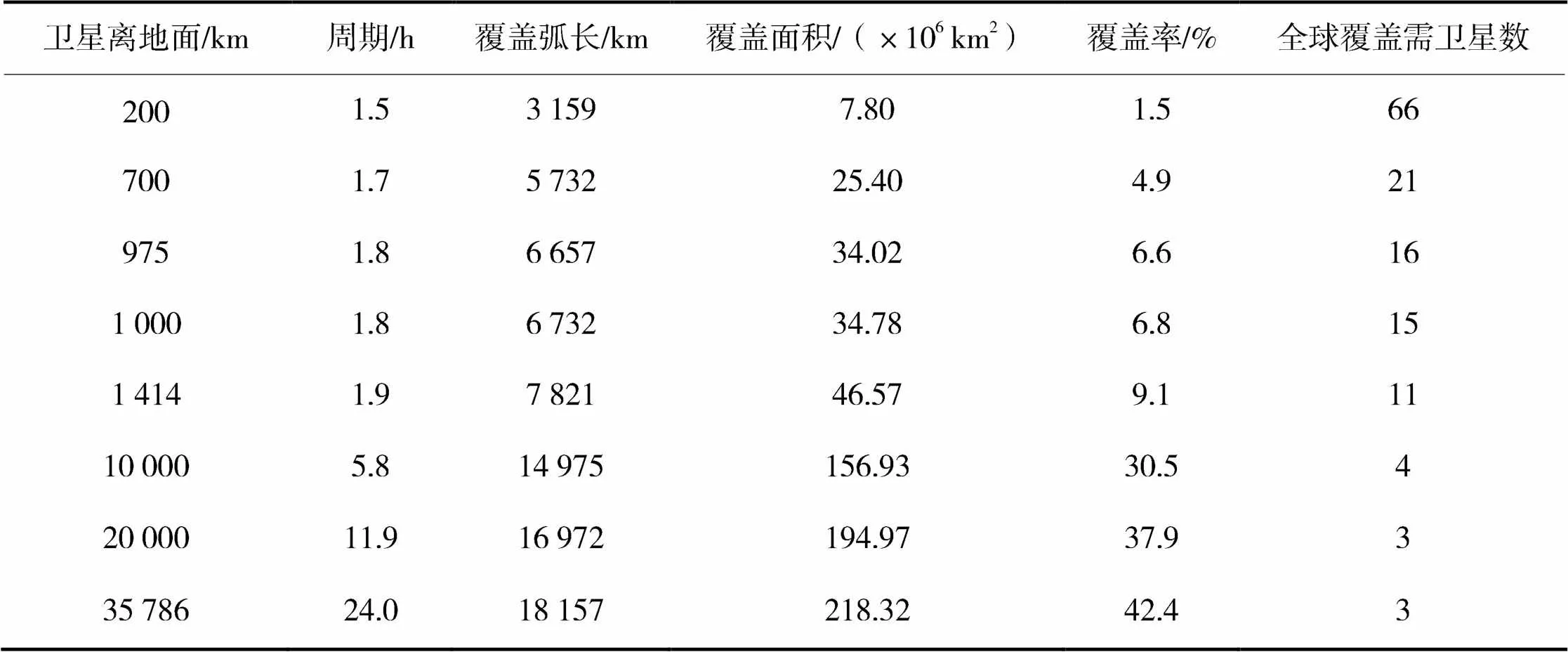
表2 不同高度卫星的覆盖情况

1.2 低轨卫星可观测弧段

上面从概念上讨论了低轨卫星全球覆盖情况，对于不同的观测站，由于地理位置不同实际可观测到的弧段在时域上是不一样的，多站可实现时域上观测互补，相应引出了不同站的调度策略。

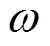
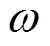
图2 卫星从轨道坐标系转换到站心坐标系

上面坐标系转换过程的数学表达式为

先研究一颗种子卫星S1（轨道参数是：轨道半长轴7 353.14 km，偏心率0，倾斜角55°，升交点赤经0°，近地点幅角0°，初始时刻真近点角0°）情况，然后根据Walker星座的特点扩到整个星座。

图3模拟长春、喀什、昆明、西安观测种子卫星时方位角和仰角的变化情况，仿真起始时刻是2020年7月25日0时，仿真时间是1d。图4模拟种子卫星对4个地面站的可见弧段，表3给出4个地面站的观测圈数和可观测的总时间。

图3 不同测控站可见种子卫星的极坐标图

图4 不同测控站可见种子卫星的观测弧段

表3 地面站观测情况

从上面仿真可见：由于测站分布在国内，测站（除喀什之外）互补性不是很大，在半天时间内几乎无法观测到卫星（低轨卫星覆盖小），在这时段内卫星无法进行测控，突显调度的困难性，因此测控地面站资源调度显得比较重要。

1.3 低轨卫星星座的可视弧段

上面研究了一颗卫星可观测弧段情况，下面扩展到整个星座可观测弧段。首先对待观测的颗卫星进行编号，图5表示卫星编号方式：前2位代表轨道的编号（1起算），后2位代表卫星在轨道内的序号（1起算）。

图5 卫星编号换算图

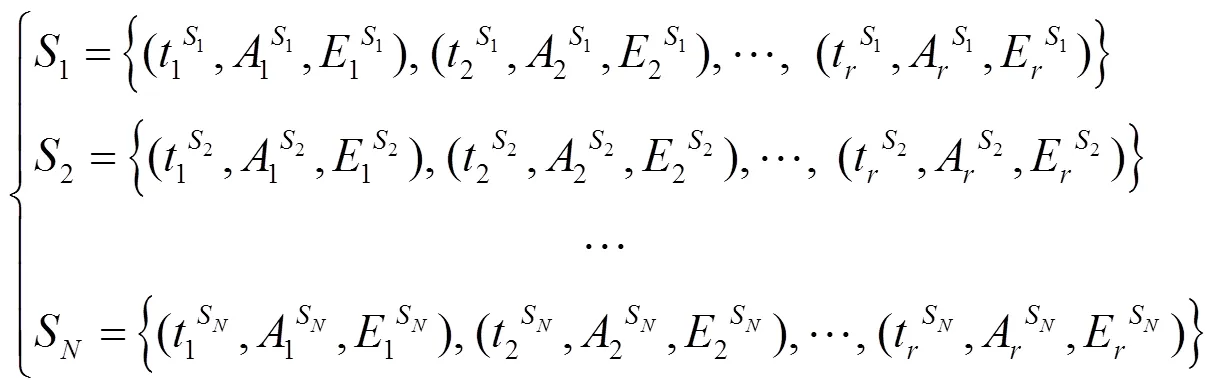
2 低轨卫星调度策略

2.1 调度策略1

调度策略1的约束条件：① 优先选择观测在某时刻被观测次数最少的卫星，使每颗卫星尽可能被均匀观测；② 其次选取俯仰角高的卫星。图6所示策略1框图，给出了4个地面站联合观测120颗低轨卫星的调度流程，如果多个站可同时观测到一颗星，则选取当前时刻最大俯仰角所对应的地面站，如果一个站可同时观测到多颗星，首先选取较长时段未被观测的卫星进行观测，其次再选取俯仰角最高的卫星进行观测。

图6 策略1调度流程图

2.2 调度策略2

调度策略2的约束条件：① 优先选择观测次数最少的卫星，使每颗卫星尽可能被均匀观测；② 其次选择连续观测时间最长的地面站。如果多个地面站可同一时间段观测到同一颗卫星，则优先选取观测时间最长的地面站；如果一个地面站可同一时间段观测到多颗星，首先选取较长时段未被观测的卫星进行观测，其次选取可观测时间最长的卫星。策略2的调度流程图见图7。

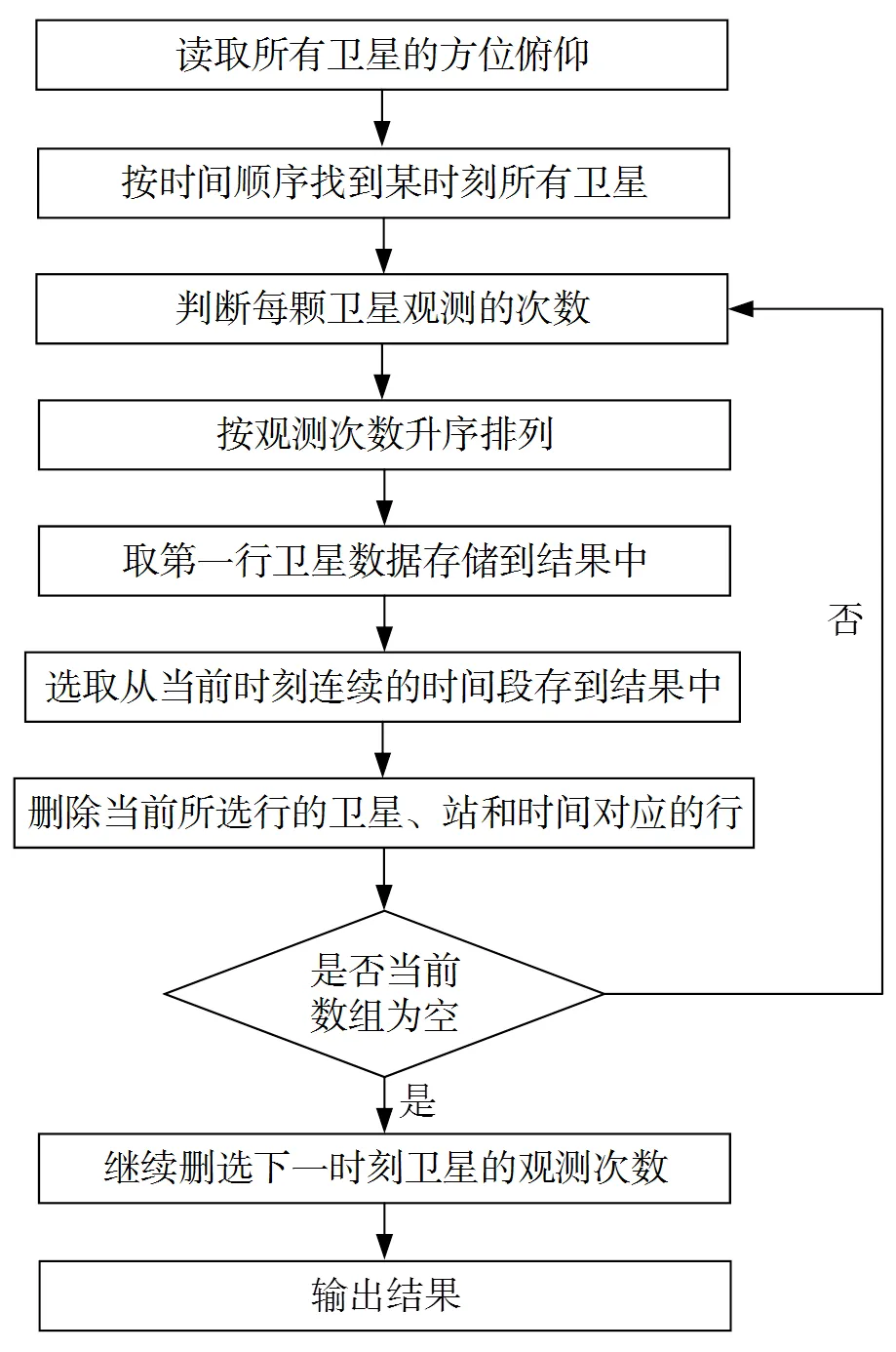
图7 策略2调度流程图

多星多站调度研究中，多星争夺地面站资源以及地面站资源的充分利用可在方案中得到解决。

3 结果与分析

3.1 仿真数据说明

本文所选仿真数据的时间是24 h，时间窗口间隔为60 s，1 d共1 440历元。选取的4个地面站分别为：长春、喀什、昆明、西安，每个地面站的天线均为单天线，天线可观测的俯仰角范围为5°～85°。星座设定为：轨道高度975 km，轨道倾斜角55°，每个轨道面是10颗卫星，共12个轨道面。先插入一颗种子卫星，通过Walker星座建立120颗卫星的卫星轨道，星座卫星运行情况见图8。

图8 卫星和地面站的分布

3.2 仿真结果分析

策略1和策略2每颗卫星观测时间比较见图9，其中，横轴代表卫星编号，纵轴代表每颗卫星的观测时间。由图9（a）可知，方案1卫星1 d最长可观测的总时间54 min，最短时间为33 min。由图（b）可知，策略2卫星最长可观测的总时间是70 min，最短时间为25 min，其余卫星的观测时间均在50 min附近波动。在两种策略中，都满足了约束条件，即每颗卫星每天至少被观测到20 min，由于地面站分布局限，卫星编号从20到40可观测的时间较短。在策略2中，卫星的观测时间变长，观测数增多。

以长春站为例，策略1和策略2的地面站可观测卫星情况见图10，横轴代表可观测时间，纵轴代表卫星编号。通过两种策略的对比发现：在0～500 min，策略1中的某时刻，被观测的卫星可能不在同一轨道平面或者下一时刻观测到的不是同一颗卫星，此时地面站需要不断切换天线以便捕捉到卫星，增加了地面站切换天线的频率。

4个地面站两种调度结果见图11和图12，通过对比发现，在图11中，观测星的原则是在某时刻选择俯仰角高的卫星，每一时刻因观测的卫星不同，导致频繁切换卫星，看似一条“直线”，实则是一些分布比较散落的点。图12中，观测星的原则是在某时刻选择连续观测时间最长的卫星，会在某一时间段内对某颗卫星进行连续观测，看似一些散落的“点”，因重叠部分较多，实则是比较连续的点。

图11 策略1的4个地面站调度卫星结果

图12 策略2的4个地面站调度卫星结果

4 结论

本文对卫星地面站调度策略作了研究，对特定的任务提出了两种不同的低轨卫星地面站调度策略。对这两种策略进行了详细研究，通过对两种策略的仿真计算，从每颗卫星的观测时间、某个地面站（本文以长春站为例）观测卫星的情况和卫星地面站调度情况进行对比，策略2对每颗卫星的观测时间长，观测卫星切换操作少，可保证均匀观测，可获取卫星至少20 min遥测遥控数据，策略2在实际应用上优于策略1，更适合实际卫星测控任务。

论文研究针对特定的星座，但是方法本身可借用于其他星座的调度研究。

[1] 贺达健. 低轨卫星网络移动性管理技术研究[D]. 长沙: 国防科学技术大学, 2016.

[2] 杨波. 低轨卫星增强导航技术研究[D]. 成都: 电子科技大学, 2017.

[3] 肖楠, 梁俊, 张基伟. 中国低轨卫星星座组网设计与规划[J]. 电讯技术, 2010, 50(12): 14-18.

[4] 赵齐乐, 刘经南, 葛茂荣. GPS导航星座及低轨卫星的精密定轨理论和软件研究[J]. 武汉大学学报(信息科学版), 2005, 30(4): 375-375.

[5] 丁欢. 基于低轨卫星增强的北斗定位系统分析[J]. 自动化应用, 2020(8): 147-151.

[6] 王乐, 燕兴元, 张勤, 等. 低轨卫星增强BDS卫星定轨技术探讨[J]. 导航定位学报, 2017, 5(4): 51-57.

[7] 吴星. 遥测遥控信号的被动解调技术[D]. 成都: 电子科技大学, 2014.

[8] 马福建. 低轨星座增强GNSS精密定位关键技术研究[D]. 武汉: 武汉大学, 2018.

[9] 关梅倩, 焦文海, 贾小林, 等. 基于导航增强的低轨卫星星座设计[C]//第九届中国卫星导航学术年会论文集—S07卫星导航增强技术, 哈尔滨: 中国卫星导航系统管理办公室学术交流中心, 2018: 22-26.

[10] GOOLEY T D. Automating the satellite range scheduling process[D]. Ohio: Air Force Institute of Technology, 1993.

[11] GOOLEY T D, BORIS J J, MOORE J T. Automating air force satellite control network(AFSCN) scheduling[J]. Mathematical and Computer Modelling, 1996, 24(2): 91-101.

[12] PEMBERTON J C, GALIBER F. A constraint-based approach to satellite scheduling[J]. Theoretical Computer Science, 2001: 101-114.

[13] 金光, 武小悦, 高卫斌. 卫星地面站资源调度优化模型及启发式算法[J]. 系统工程与电子技术, 2004, 26(12): 1839-1841+1875.

[14] 金光, 武小悦, 高卫斌. 基于冲突的卫星地面站系统资源调度与能力分析[J]. 小型微型计算机系统, 2007, 28(2): 310-312.

[15] BURROWBRIDGE S E. Optimal allocation of satellite network resources[D]. Virginia: Virginia Tech, 1999.

[16] BARBULESCU L, WATSON J P, WHITLEY L D, et al. Scheduling space-ground communications for the air force satellite control network[J]. Journal of Scheduling, 2004, 7(1): 7-34.

[17] 贺仁杰, 谭跃进. 基于约束满足的卫星地面站资源优化分配问题研究[J]. 计算机工程与应用, 2004, 40(18): 229-232.

[18] WOLFE W J, SORENSEN S E. Three scheduling algorithms applied to the earth, observing systems domain[J]. Management Science, 2000, 46(1): 148-168.

[19] 王军民, 谭跃进. 多星联合动态调度问题的启发式算法研究[J]. 计算机工程与应用, 2007, 43(21): 21-25.

[20] 杨霞, 李建成. Walker星座星间链路分析[J]. 大地测量与地球动力学, 2012, 32(2): 143-147.

Research on schedule strategy of ground stations for LEO satellites

AN Yuan-yuan1,2,3, LI Wei-chao1,2, WANG Wei1,2, YANG Xu-hai1,2,, WEI Pei1,2,3, WANG Xiao1,2

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Precise Positioning and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)

Recently, with the rapid development of low-orbit constellations for various purposes, the requirements of ground stations are also increased. According to mission requirements and constraints, it is necessary to find an optimal strategy for the resource scheduling of ground stations used for telemetry, track and command (TT&C). This paper focuses on the schedule strategy of ground stations to track of the specific low-orbit satellites, i.e., Walker constellation, for the purpose of TT&C, data transmission and other measurements. The basic principle of scheduling is to give high priority to the satellites that are in urgent need of data transfer. According to such principle, two schemes are proposed: (1) selecting the satellite with the highest elevation angle. (2) selecting the satellite with the longest continuous observation time. There are currently four ground stations: Changchun, Kashi, Kunming, and Xi’an, all of which are equipped with single antenna. The properties of the two schemes are studied through simulation and the result shows that: although both of the two schemes can achieve the scheduling aim, the antennas switch frequency of scheme 2 is lower than that of scheme 1. Therefore, in general, the scheme 2 is better than the scheme 1.

low-orbit satellite; TT&C station; resource scheduling; optimized simulation

10.13875/j.issn.1674-0637.2021-02-0120-12

安元元, 李伟超, 王伟, 等. 一种低轨卫星星座测控地面站调度策略研究[J]. 时间频率学报, 2021, 44(2): 120-131.

2020-11-08；

2020-12-18

北斗专项重点资助项目（Y616ZF2S00）；中国科学院青年创新促进会会员资助项目（1188000LWC）