混凝土密肋式锥面网壳的动力特性分析*
杨水艳,张华刚*,2,马克俭,2
(1.贵州大学 空间结构研究中心,贵州 贵阳 550025;2.贵州省结构工程重点实验室,贵州 贵阳 550025)
我国薄壁结构最早使用于20世纪40年代后期,如1948年在常州建成的一个仓库便是用了圆柱面壳体结构[1]。因薄壁结构曲面施工困难和理论计算复杂等问题,至60年代后期,薄壁结构的使用逐渐萧条。近年来,数值计算技术的发展使薄壁结构的计算分析变得较为容易,但施工困难是尚未有效解决的问题,因此,我国许多学者致力于壳体结构的形式创新研究。马克俭等[2]提出了将空腹夹层板弯曲成曲面形式的空腹网壳结构,并于2008年在中国电建集团贵阳勘测设计院会议中心工程中成功应用。常玉珍等[3]提出了外包U型钢的组合肋壳结构。金杰等[4]在钢管中注入混凝土而提出了钢管混凝土网壳结构。上述结构形式推动了壳体结构的发展。
为有效解决混凝土曲面支模难和降低工程造价等问题,张华刚等[5-8]提出由密肋平板在脊线处交汇形成新型混凝土折板式密肋网壳。其中,混凝土人字形折板式密肋网壳已成功运用到实际工程中。在关岭美食城工程中,用钢量仅为43.0 kg/m2,可见这类新型结构的用钢量较低,具有良好的经济技术指标。
为了解混凝土密肋式锥面网壳结构的动力特性,基于数值模拟分析,采用子空间迭代法[9]求解结构自振频率及振型,以期为这种结构的抗震分析提供参考。
1 结构形式及算例基本情况
1.1 结构形式
结构形式如图1所示。通过将圆锥沿曲面等分切割成三角形密肋平板,再由密肋平板在脊线处交汇形成锥面网壳。密肋梁网格采用正交正方的形式布置,在边梁与脊线交汇处设置支座,并约束其全部自由度。
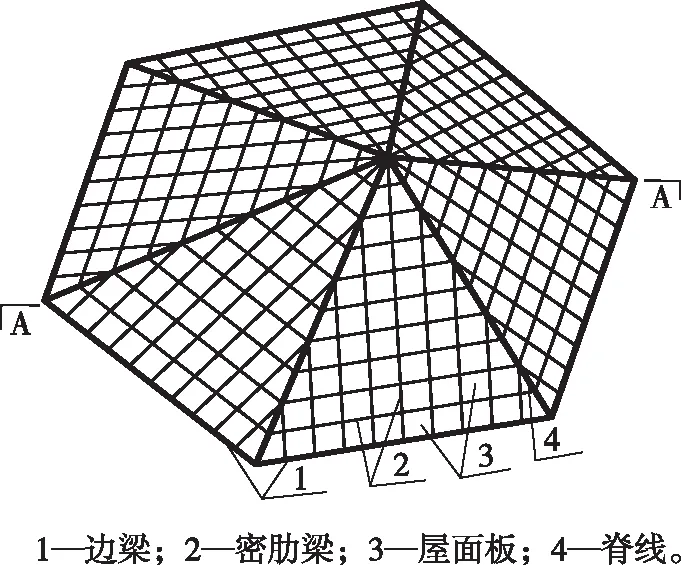
图1 网壳锥面结构
1.2 算例情况
如图2所示,结构跨度为30 m,矢高为7.5 m,经承载力设计后,屋面板厚为60 mm,边梁截面尺寸为400 mm×800 mm,脊线截面尺寸为300 mm×700 mm,密肋梁截面尺寸为150 mm×400 mm。结构自振分析时,屋面板采用板壳单元,其余构件均采用空间梁单元,混凝土材料的弹性模量Ec=3.25×104N/mm2,泊松比v=0.2,钢筋混凝土密度为2.42×103kg/m3;结构不计自重的恒载取5.0 kN/m2,上述均为本文所有算例的共性参数。
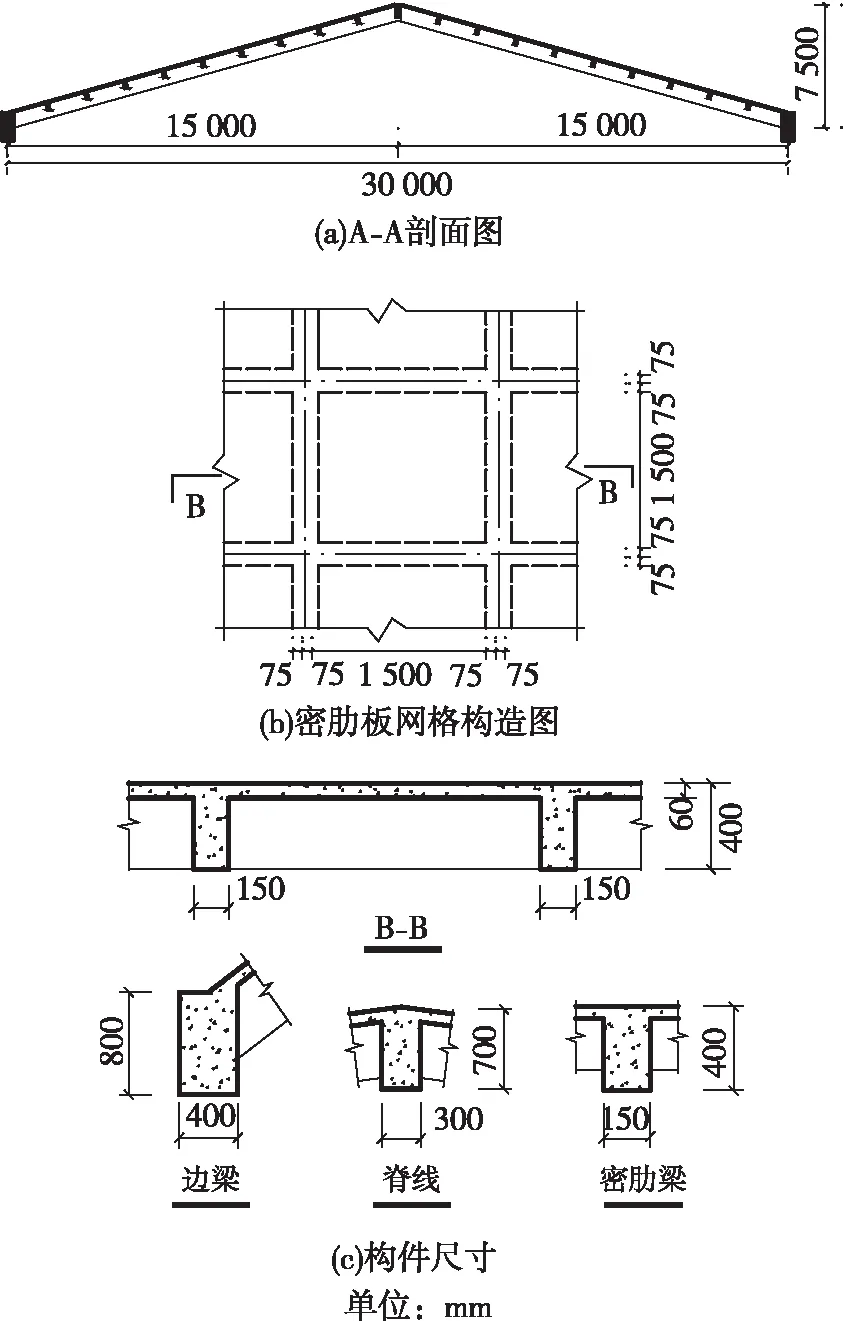
图2 结构布置及几何尺寸
2 自振特性分析
2.1 自振频率
结构前50阶自振频率如图3所示。频谱分布较为密集,且随振型阶数的增大有明显的跳跃性,可见结构刚度分布较为均匀,结构成对出现的振型较多,这是结构有多条对称轴的缘故[10-12]。
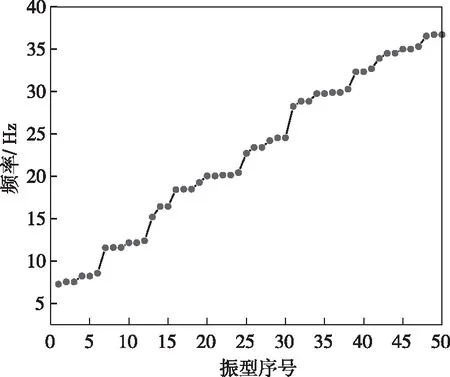
图3 结构前50阶自振频率
2.2 振型
结构前9阶振型如图4所示。低阶振型主要以竖向振动为主,模态坐标较大区域位于边梁附近的密肋平板上。第1阶振型沿环向关于脊线各有6个半波反对称振动,第2~5阶振型呈现2个半波振动,第6阶振型沿环向关于脊线各有6个半波正对称振动,第7~9阶振型在每块密肋平板上均出现多个振动区域。低阶振型的振动节线大体为脊线,可见脊线对结构具有拱向支承的作用。
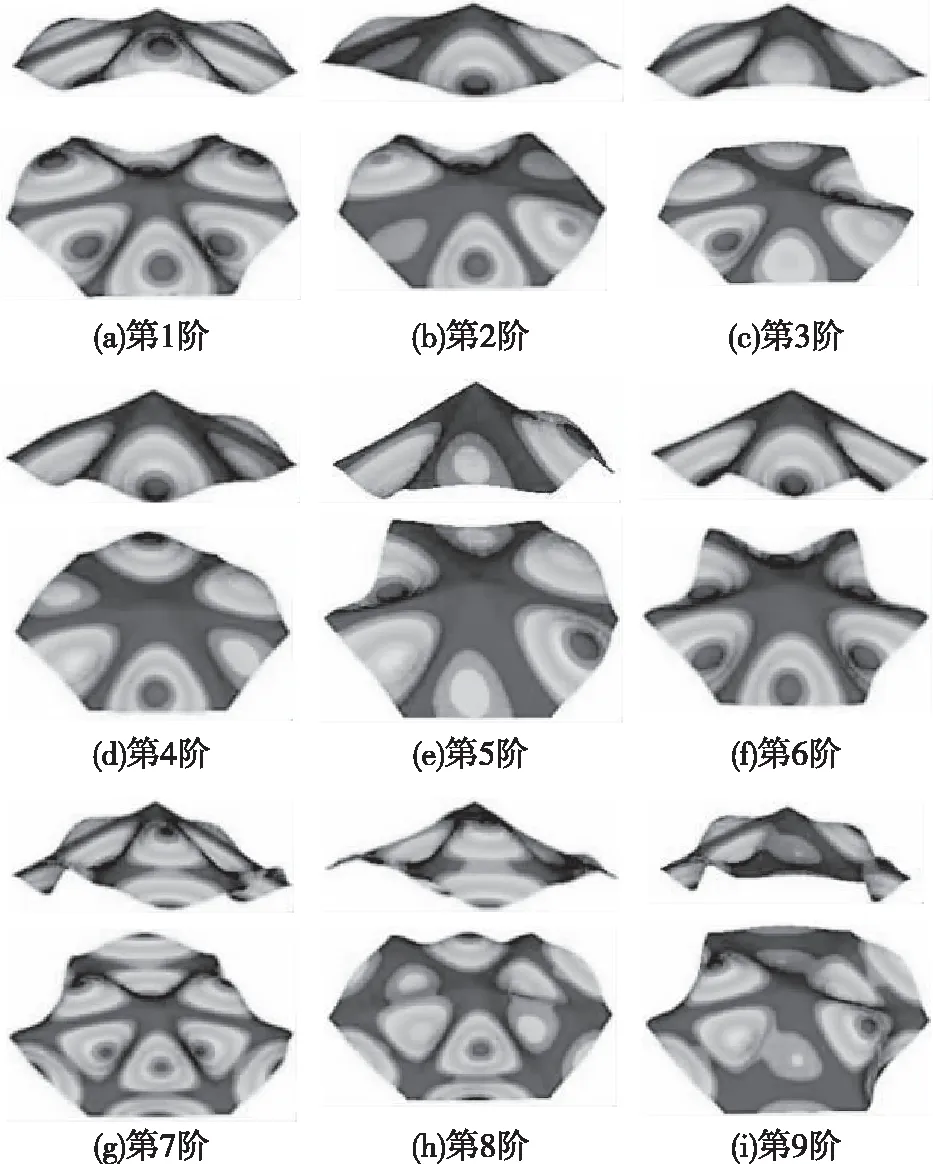
图4 屋盖的前9阶振型图
综上分析,结构第1阶竖向振动频率可近似反映其整体刚度。在下文参数化分析时,主要考察不同因素对结构基频的影响[13]。
3 自振频率的参数化分析
3.1 参数化分析算例
在基本算例的基础上,分别考虑矢跨比、边梁刚度、脊线刚度、密肋梁刚度和屋面板厚等因素对结构基频的影响。算例取值情况如下:
1)仅改变屋盖矢跨比计算6个算例,矢跨比分别取1/8、1/7、1/6、1/5、1/4和1/3。
2)考虑边梁刚度的影响时,主要通过改变其截面高度实现,脊线截面高度取650 mm,边梁截面高度分别取700、750、800、850、900、950 mm。
3)考虑脊线刚度的影响时,边梁截面高度取900 mm,脊线截面高度分别取600、650、700、750、800、850 mm。
4)考虑密肋梁刚度的影响时,密肋梁截面高度分别取300、350、400、450、500、550 mm。
5)考虑板厚的影响时,屋面板厚分别取50、60、70、80、90、100 m。
3.2 矢跨比的影响
改变屋盖矢跨比对基频的影响如图5所示。基频随着矢跨比的增大而持续减小。由图5可见:当矢跨比为1/8时,基频为8.19 Hz;当矢跨比为1/3时,基频为6.57 Hz,基频降幅约为19.8%;矢跨比在1/8~1/5范围内基频变化率较小,这是因为随着矢跨比的增加,结构的展开面积增大,在网格数不变时,将降低结构整体刚度,并增大结构质量。在考虑结构网格数不变的情况下,相当于间接稀疏了斜板的部分网格,从而导致结构刚度的减小。因此,矢跨比的改变对结构刚度影响较为明显,建议结构矢跨比的选取不宜大于1/5。
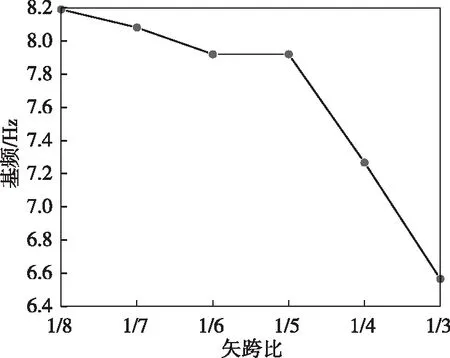
图5 矢跨比对基频的影响
3.3 边梁刚度的影响
边梁刚度的改变对基频的影响如图6所示。随着边梁截面高度的增大,结构的基频不断增大。由图6可见:当边梁截面高度为700 mm时,基频为6.72 Hz;当边梁截面高度为950 mm时,基频为7.88 Hz,基频增幅约为17.3%。边梁作为结构的主要传力构件,增大边梁的刚度会加强对密肋梁的约束,进而延缓结构变形,提高结构整体刚度。因此,改变边梁刚度对提高结构整体刚度有一定贡献,建议边梁截面高度的取值宜按跨度的1/40~1/30确定。
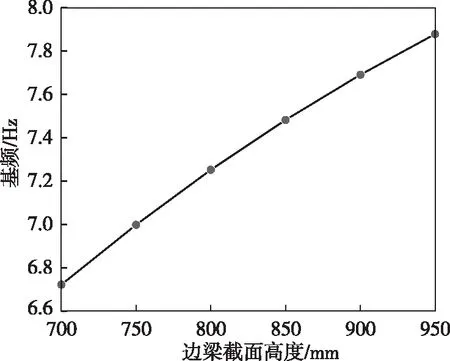
图6 边梁刚度对基频的影响
3.4 脊线刚度的影响
脊线刚度对结构基频的影响如图7所示。提高脊线刚度对结构的基频影响较小。由图7可见:当脊线截面高度为600 mm时,基频为7.67 Hz;当脊线截面高度增到850 mm时,基频为7.75 Hz,基频增幅仅为1.0%。因为脊线成拱后自身刚度较大,而密肋平板才是结构变形的薄弱环节,因此,增大脊线截面高度对结构整体刚度的提高效果不明显,脊线截面高度的选取满足强度设计要求即可。
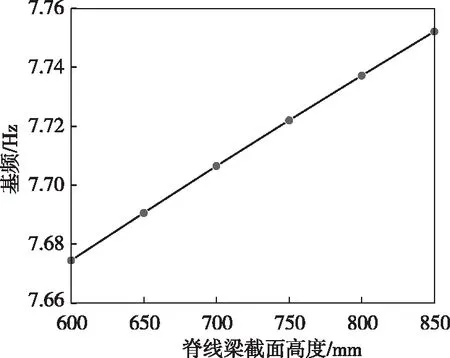
图7 脊线刚度对基频的影响
3.5 密肋梁刚度的影响
密肋梁刚度的改变对基频的影响如图8所示。基频随着密肋梁刚度的增大而增大。由图8可见:当密肋梁截面高度取300 mm时,基频为6.51 Hz;当密肋梁截面高度取 550 mm时,基频为8.05 Hz,基频增幅约为23.7%。因结构整体刚度受密肋平板控制,加大密肋梁刚度可直接增大每块密肋板的刚度,进而明显提高屋盖整体刚度,但过大的密肋梁刚度会加大结构自重。密肋梁截面高度的选取宜按跨度的1/100~1/75确定。
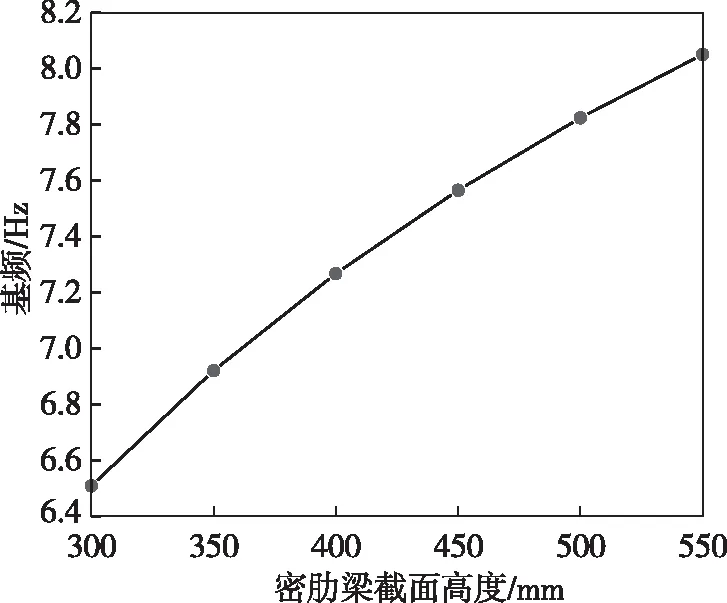
图8 密肋梁刚度对基频的影响
3.6 板厚的影响
屋面板厚的改变对基频的影响如图9所示。随着屋面板厚的增大,基频呈持续下降的趋势。由图9可见:当屋面板厚为50 mm时,基频为7.46 Hz;当屋面板厚为100 mm时,基频为6.67 Hz,基频降幅约为10.6%。
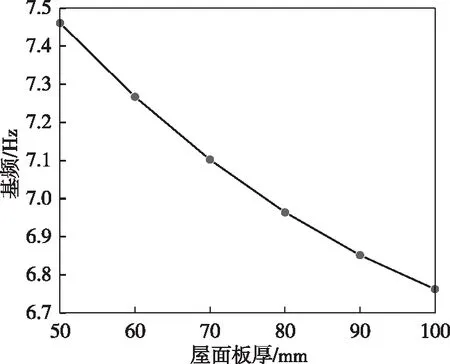
图9 屋面板厚对基频的影响
综上分析可得,屋面板厚度增加对结构刚度的贡献不足以抵消其质量增加对基频的影响,而质量增加又会加大地震作用,因此,建议屋盖板厚选取满足构造要求即可。
4 基频公式拟合
4.1 等效刚度的计算
由上述数值模拟分析可知,结构的刚度由边梁、脊线、密肋梁和屋面板厚提供,可将其连续化进行等效刚度的计算[14]。根据图10分别计算密肋梁的等效薄膜刚度B1和等效抗弯刚度D1分别为:
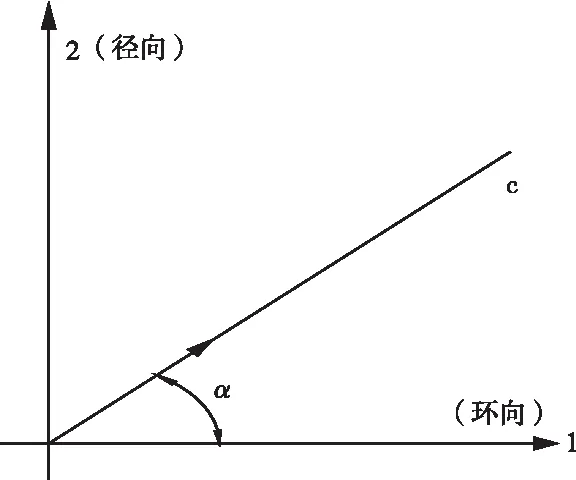
图10 密肋梁的等效刚度计算
(1)
(2)
式中:E为弹性模量;A1为环向肋的截面面积;S1为环向肋间距;Ac为脊线截面面积;Sc为脊线的肋间距;α为脊线与环向肋的夹角;I1为环向肋的惯性矩;Ic为脊线惯性矩。
屋面板的薄膜刚度和抗弯刚度分别为:
(3)
(4)
式中:t为板厚;v为泊松比。
结构的等效薄膜刚度B和等效抗弯刚度D分别为:
B=B1+Bb
(5)
D=D1+Db
(6)
4.2 基频公式拟合
基频f与相关物理量的散点图如图11所示。
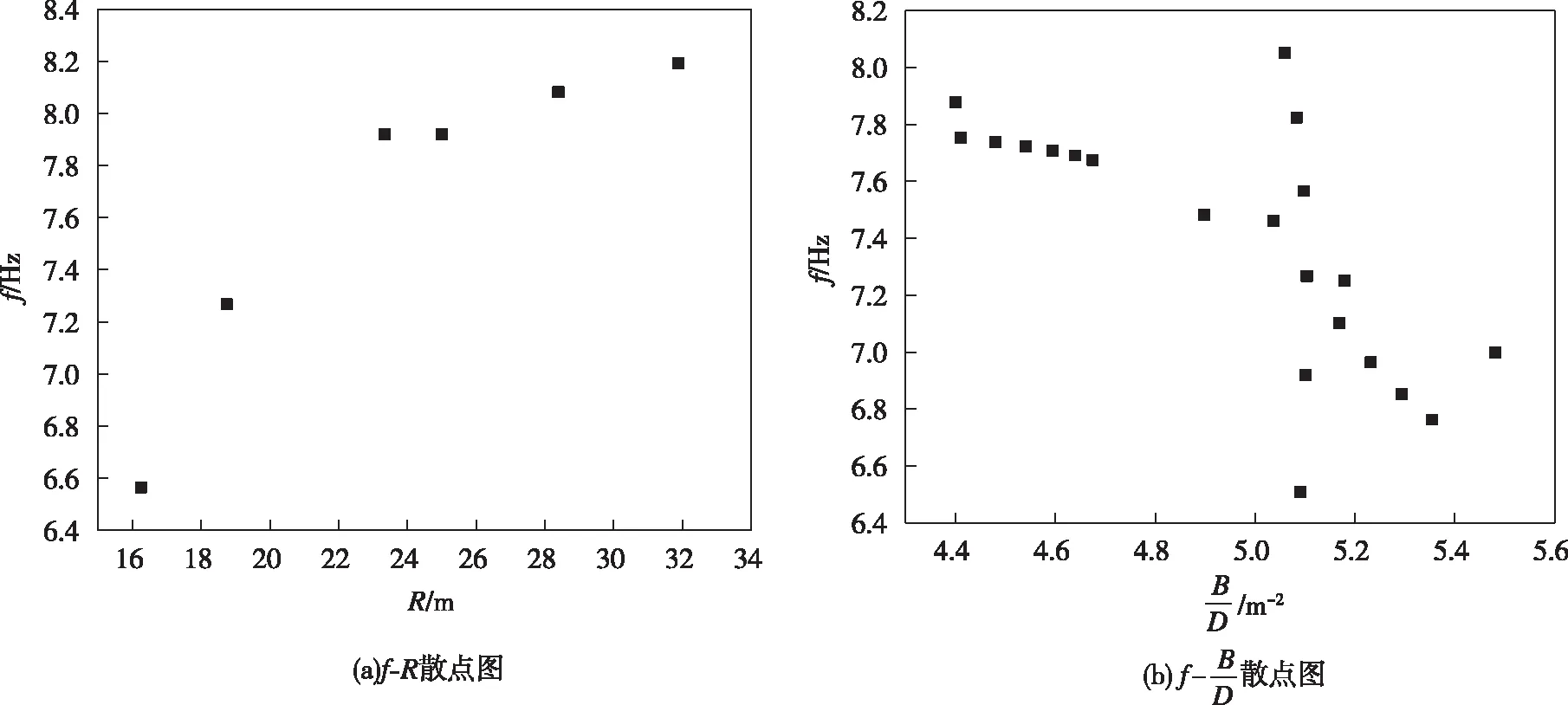
图11 基频与相关物理量的散点图
f与B/D大致呈线性关系,与R整体又呈曲线关系。根据其特点将基频函数关系设为[14]
(7)
其中:
(8)
式中:R为圆锥面的曲率半径[15];L为跨度;γ为矢跨比;待定参数K、a、b、c需依据理论结果由拟合确定。则按最小二乘法, 可得基频的近似计算公式为
(9)
基频误差计算公式为
(10)
结构基频理论值与拟合值对比分析结果见表1。误差在15%以内,在工程精度可接受范围内。
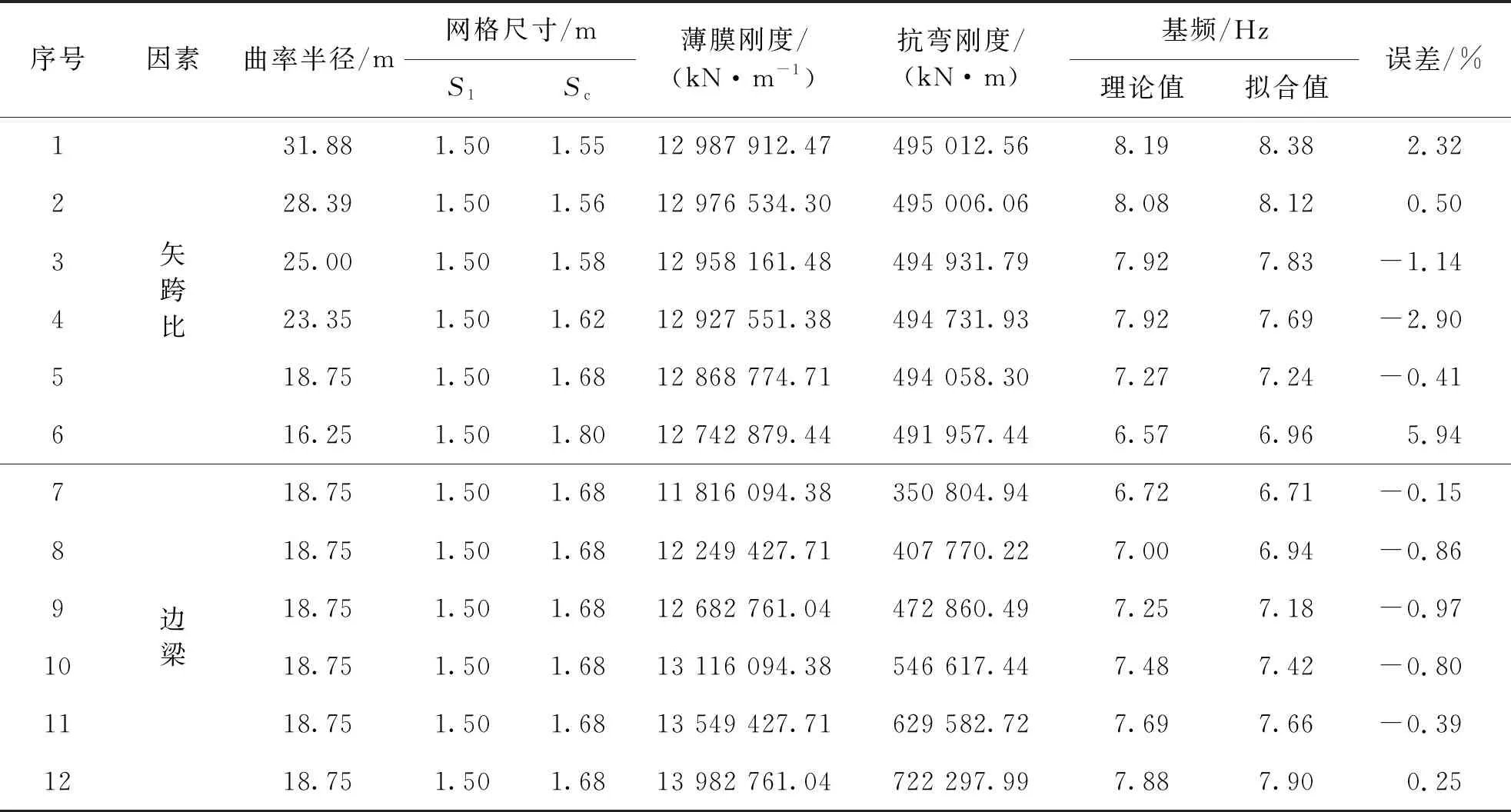
表1 结构基频拟合值及理论值对比结果
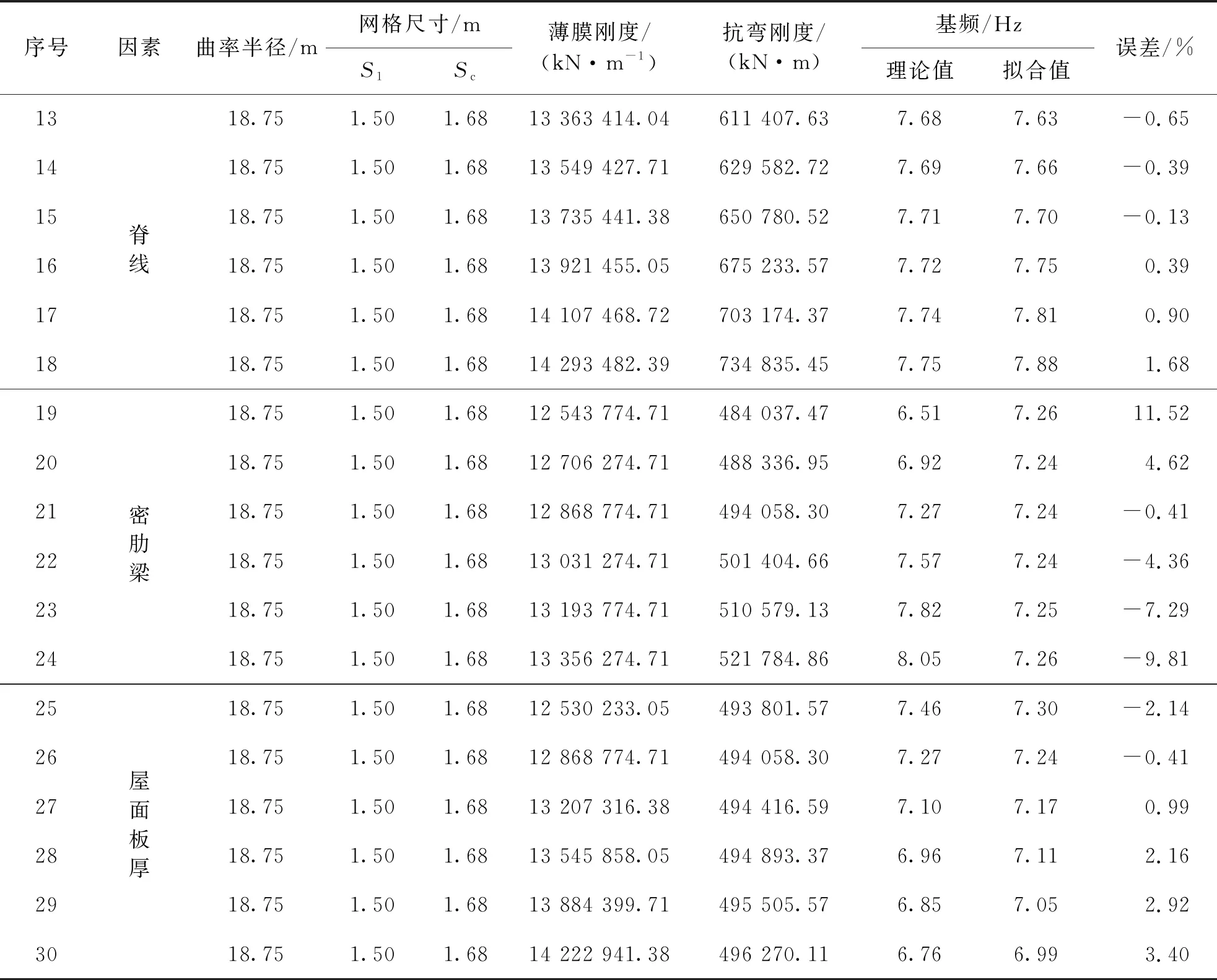
续表
5 结语
1)结构的振型以竖向振动为主,且在密肋折板中下区域的竖向振动出现较早。因结构刚度分布均匀,频率多次“重频”且有明显的跳跃点。
2)网格数不变时,增大结构矢跨比对结构整体刚度的控制是不利的,建议选取屋盖矢跨比不宜过大。
3)边梁刚度的增大会加强对密肋板的约束,进而提高结构整体刚度。建议边梁截面高度的选取宜按跨度的1/40~1/30确定。
4)脊线是振动节线,且其成拱后自身刚度较大,因此,增大脊线刚度对提高结构整体刚度效果不明显。
5)增大密肋梁刚度对提高结构整体刚度的影响较大,但大的密肋梁高度会加大结构自重,密肋梁截面高度的取值宜按跨度的1/100~1/75确定。
6)结构基频的拟合公式计算误差能满足工程设计精度。

