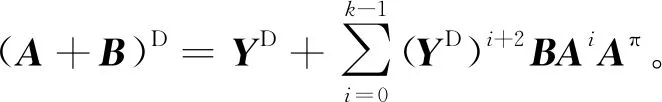矩阵之和Drazin逆的简单表示*

杨晓英,王亚强,刘 新

(1.四川信息职业技术学院 基础教育部,四川 广元 628017;2.宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013)

设Cm×n表示m×n阶复矩阵的集合，A∈Cn×n,若X∈Cn×n满足下列方程[1]：

Ak+1X=Ak,XAX=X,AX=XA

则称X为A的Drazin逆,记作X=AD，称k为A的指数，记作ind(A)=k。记Aπ=I-AAD。矩阵的Drazin逆是矩阵广义逆的一种类型,如果矩阵的Drazin逆存在必唯一。 矩阵的Drazin逆在信息安全、图像增强以及神经网络中有着广泛的应用， 这也促使许多学者执着于是否可以在没有任何限制条件的情况下给出Drazin逆的表示。 直到现在，两个矩阵之和在没有条件下的Drazin逆表示仍然是一个开放性的问题。 一些学者已经讨论了两个矩阵之和在特定条件下Drazin 逆的表示结果，见文献[1-6]。 本文通过对其中一个矩阵进行核-幂零分解，然后结合Drazin逆的性质和利用已有引理，给出两个矩阵之和分别在AπBA=0和AπB=0条件下Drazin逆的简单表示。

为了给出两个矩阵之和Drazin逆的新表示，首先给出几个重要的引理。

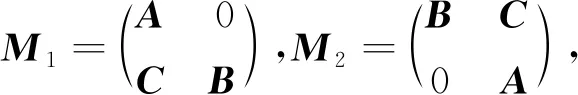
其中

引理2[8]1)如果PQ=0,Q是s-幂零的,则

2)如果PQ=0,P是s-幂零的,则

1 主要结果

下面，我们应用以上引理给出在AπBA=0和AπB=0条件下两矩阵之和Drazin逆的表示。

首先，给出两矩阵之和在AπBA=0条件下Drazin逆的表示。

定理1设A,B∈Cn×n，如果AπBA=0，则

其中，Y=(A+B)ADA，ind(A)=k，max{ind(A),ind(B)}≤m≤ind(A)+ind(B)。

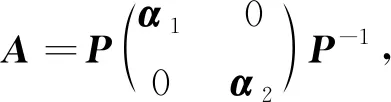
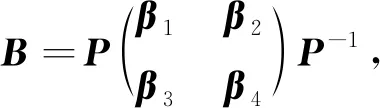
β1∈Ck×k，由

可得：β3α1=0，β4α2=0。

由α1为非奇异的，得β3=0，所以

由引理1，得

其中

(α1+β1)Dβ2(α2+β4)D

其中，ind(α2+β4)=r，ind(α1+β1)=s。

由于β4α2=0，α2为k阶 -幂零矩阵，由引理2， 得

(1)

由

Y=(A+B)ADA

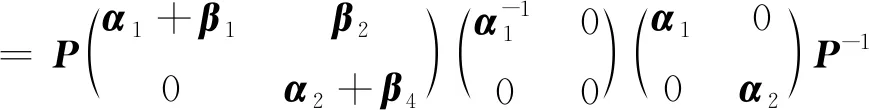
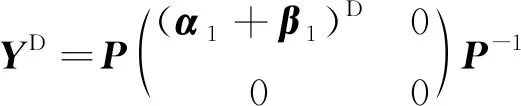
由

AπAi(BD)i+1

进而有

由式(1)，显然

(α2+β4)π=I-(α2+β4)D(α2+β4)

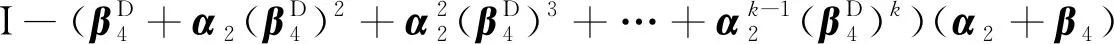
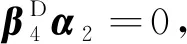
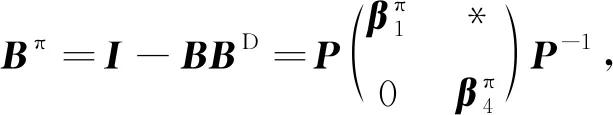
所以

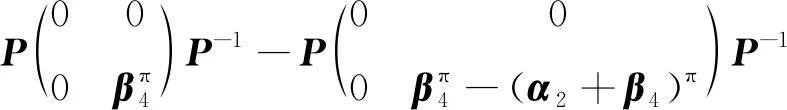
接下来我们计算，

((α1+β1)D)j+2β2(α2+β4)j(α2+β4)π

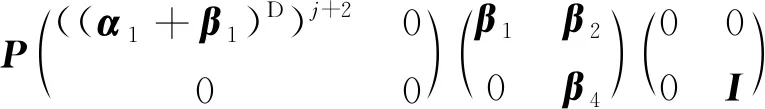
综合以上式子，得

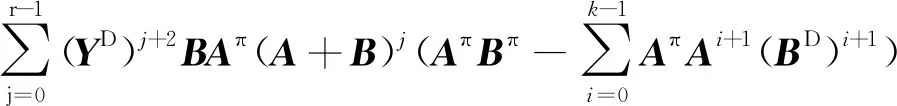
其中，Y=(A+B)ADA。

下面，我们应用以上引理，给出在AπB=0条件下两矩阵之和Drazin逆的表示。

定理2设A,B∈Cn×n，如果AπB=0，ind(A)=k，则

其中，Y=(A+B)ADA。

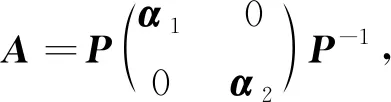
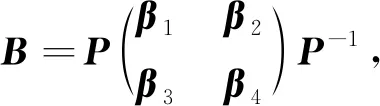
β1∈Ck×k。

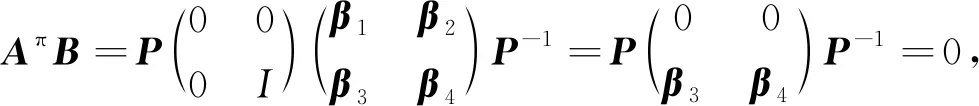
易得：β3=0，β4=0。

所以

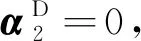
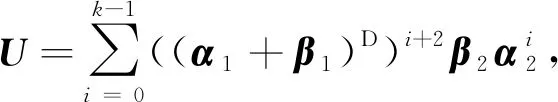
(YD)i+2BAiAπ=