一种惯性测量单元标定补偿方法

陈健 杨富锋 靳展

（南京理工大学发射动力学研究所 江苏省南京市 210094）

1 引言

因为尺寸小、成本低、精度高、易于集成和可大规模生产等优点，微机电（MEMS）惯性传感器受到越来越多人们的欢迎，广泛应用于民用和军用领域[1-3]。但由于尺寸与成本的因素，大多数MEMS陀螺仪的零偏稳定性都不是很高，有的甚至达到100°/h。此外，大多数MEMS 传感器的应用场合是低动态的，加速度在应用过程中整体较小，由其带来的输出误差即g 值敏感系数误差相比零偏稳定性等带来的输出误差可以忽略，在陀螺仪的标定中通常不做考虑[4]。因而，很少有参考文献关注研究g 值敏感系数的标定和补偿。

同时，在传统的误差标定补偿方面，常采用静态旋转多位置方法、动静结合方法进行标定[5-7]。为了考虑地球角速度对陀螺仪各方向输出的影响，需要对转台进行复杂的寻北操作来消除载体坐标系与东北天坐标系不重合带来的误差。常用的寻北装置为陀螺经纬仪，操作使用复杂，需要操作人员具有娴熟的操作经验和较高的专业素质，而且测试前期的准备时间较久，不利于实验的快速进行。

因此，本文结合以上两个问题设计了一种考虑g 值敏感系数的无需寻北的标定补偿方法，具有良好的参考和研究意义。

2 惯性测量单元误差模型建立

惯性测量单元传统的误差模型，主要基于零偏漂移误差、标度因数误差、非正交性误差、随机漂移误差这四项建立[8-10]，误差模型分别如下所示：

2.1 陀螺仪

表1：静态十二位置法标定的陀螺仪与加速度计输入

表2：陀螺仪各项误差系数标定结果

表3：加速度计各项误差系数标定结果

表4：12 个位置的均值与均方差

表4：12 个位置的均值与均方差

是否考虑g 值敏感系数 均值（°/h） 均方差是15.274 0.1465否16.748 1.1863

式（1）中，ωi、Wgi、Fgi、Kgij、εgi、δgi（i=x,y,z j=x,y,z）分 别为陀螺仪的三轴输入、输出、标度因数、安装误差、零偏与随机误差，陀螺仪模型可简写为如下形式：其中，Kg、εg、δg为包含陀螺仪各项误差系数的矩阵，ω、Wg为陀螺仪的输入输出矩阵。

2.2 加速度计

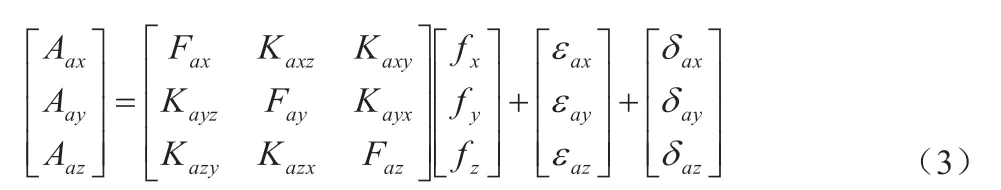
式（3）中，fi、Aai、Fai、Kaij、εai、δai（i=x,y,z j=x,y,z）为加速度计的三轴输入、输出、标度因数、安装误差、零偏与随机误差，加速度计模型可简写为如下形式：

其中，Ka、εa、δa为包含加速度计各项误差系数的矩阵，f、Aa为加速度计的输入输出矩阵。

由于随着科学技术的发展与MEMS 技术的进步，MEMS 传感器精度不断提升，陀螺仪的零偏不稳定性等误差较大的情况逐步改善，g值敏感系数所引起的误差占比逐步上升，已经不能够轻易忽略；此外，高精度MEMS 传感器的应用场合也随着精度的提升而扩展，高动态的应用场合越来越多。因此，在高性能MEMS 陀螺仪中，也需要对g 值敏感系数进行标定和补偿，以提高陀螺仪的测量精度和动态性能。

结合以上问题与情况的考虑，考虑g 值敏感系数建立陀螺仪新的误差模型。

式（5）中，Gij(i=x,y,z,j=x,y,z)为MEMS 陀螺仪的三轴g 值敏感系数，其余参数同式（1）所示。

简化形式为：

3 IMU标定方案确定

传统标定方法需要感应地球自转角速度在东北天三轴分量作为标定依据，因此需要在标定前对转台进行寻北，以使载体坐标系与东北天坐标系重合。本文设计了一种考虑g 值敏感系数的无需寻北12 位置标定补偿方法，具体步骤如下：

3.1 STIM300的转台静态输出数据采集与处理

将STIM300 固定安装在三轴转台内框中，X 轴指向天向，旋转内框调整IMU 初始位置使其Y 轴与中框法线重合，这样中框旋转不会带来天向的误差，此时内外框法线重合。由于未进行寻北操作，初始位置IMU 的Z 轴只是大致为北，即内外框的初始法线与真北方向存在一个未知的小误差角α，选取十二位置法进行标定，每个位置以及陀螺和加速度计的输入值如表1 所示。

操控转台将其旋转到表1 所示的12 个位置，每个位置都静止采集半小时数据，对每一个位置处采集的数据进行均值化处理，消除随机噪声带来的随机误差的影响。经过均值化处理后，得到12个位置的MEMS 陀螺仪与加速度计输出为：

3.2 陀螺仪和加速度计的零偏计算

考察表1 中12 个位置的陀螺仪与加速度计输入，易见各方向其和可以正负抵消，因此将这些位置的输出进行叠加求和计算后，地球自转角速率和重力加速度项可以消去，得出陀螺仪和加速度计的零偏误差如下：

其中，εgx、εgy、εgz、εax、εay、εaz为陀螺仪与加速度计的三轴零偏误差；Wigx、Wigy、Wigz、Aiax、Aiay、Aiaz为陀螺仪与加速度计在12 个位置的X、Y、Z 轴输出的均值。

3.3 STIM300的转台动态速率实验数据采集

控制转台转动，依次将IMU 的X 轴、Y 轴、Z 轴指向天向，使惯性测量单元转台绕X 轴、Y 轴、Z 轴旋转，通过转台速率控制依次输入各档速度：±100°/s、±200°/s、±300°/s。每次速率实验采集10 分钟的微惯性测量单元输出数据。

当采集完每个轴的6 次速率实验的MEMS 陀螺仪输出数据后，进行均值化处理消除随机噪声带来的随机误差的影响。同时利用整圈标定法可以减少地球自转角速率对陀螺仪输出的影响，使其水平轴的分量在转台旋转整周时被平均掉。经过整周均值化处理后，得到18 次速率实验的MEMS 陀螺仪三轴输出为：

图1：STIM300 示意图

图2：三轴多功能测试转台

其中，i=X±、Y±、Z±表示试验中转台绕x，y，z 轴旋转，+/-表示转台正转或反转，j 表示转台转速为100°/s、200°/s、300°/s时的实验数据。

3.4 MEMS加速度计的标度因数与安装误差计算

由加速度计的误差模型式（3）及其简化形式（4）可知，标度因数与安装误差的值均可由矩阵Ka得到，所以只要求得矩阵Ka的值，就能计算出标度因数与安装误差的值。由于随机误差由数据的均值化处理基本消去，从而可以列出12 个位置加速度计输出与输入的关系。

式（12）可简化为：

其中，加速度计零偏由式（10）已计算出，则A，B 均为已知数，Ka可通过线性最小二乘法求得：

由Ka可得加速度计的标度因数与安装误差值。

3.5 陀螺仪的标度因数与安装误差计算

同上可知，陀螺仪的标度因数与安装误差计算可转化为Kg矩阵的求解。考察速率实验陀螺仪与加速度计输入，由于正反转只有旋转轴的陀螺仪输入不同，两者取差后可消去零偏与g 值敏感度的影响，以绕X 轴旋转的一组正反转数据为例：

结合速率实验的所有数据可以列出陀螺仪输出与输入的关系：

式（16）可简化为：

其中，A，B 均为已知数，Kg可通过线性最小二乘法求得：

由Kg可得陀螺仪的标度因数与安装误差值。

3.6 陀螺仪的g值敏感度计算

陀螺仪的g 值敏感度计算也可转化为G 矩阵的求解。考察静态标定中12 个位置的陀螺仪与加速度计输入，易见1 与2，3 与4，5 与6，7 与8，9 与10，11 与12 位置的陀螺仪输入可通过两两相加消除北向误差角α 的影响，以位置1 与2 的数据为例：

结合静态12 位置标定的所有数据可以列出陀螺仪输出与输入的关系：

式子可简化为：

其中，A，B，Kg，εg均为已知数，G 可通过线性最小二乘法求得：

由G 可得陀螺仪的标度因数与安装误差值。

综上，即可计算出陀螺仪与加速度计的各确定性误差参数值，通过下式对陀螺仪和加速度计输出进行补偿，其中 和 为补偿了确定性误差后的陀螺仪与加速度计输出。

4 实验与结果分析

本文使用的STIM300 是一款小型、无GPS 辅助的IMU，内置3 个倾角仪以确保精准的系统调平，对磁场不敏感且进行了全温补偿，所有的轴都相对封装基准面进行了机械和电气对准，适合各种商用、军用制导及惯性导航应用。其示意图与标定所使用的三轴转台如图1 和图2 所示。

首先利用传统的静态24 位置试验与速率试验结合的标定方法对该IMU 系统进行标定。然后，采用本文提出的不寻北12 位置标定方法对该IMU 进行标定，试验结果如表2 和表3 所示。

从上述标定结果可以看出，不寻北12 位置标定方法精确地标定出了陀螺仪与加速度计的，在不需要寻北的情况下，该方法的标定精度与传统标定方法的标定精度相当。

接着，为了考察求得的g 值敏感度补偿结果的作用，分别对静态12 位置的陀螺仪输出进行包含g 值敏感度的补偿以及传统方法的补偿。考察表2.1 中各位置的陀螺仪输入，由于静态时IMU 只受地球自转角速度与重力加速度影响，易见：

由于地球自转角速率的模值ωe=15°⁄h，易见考虑g 值敏感系数的结果与真实值更为接近。

5 结论

本文提出的标定方法与传统方法相比具有无需寻北，方便快捷的特点，且考虑了g 值敏感误差的影响，对于像文中这种高精度IMU 来说，有效地减少MEMS 陀螺仪因加速度所引起的g 值敏感误差，提高了陀螺仪的动态性能和测量精度，具有重要的工程应用价值。