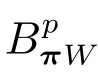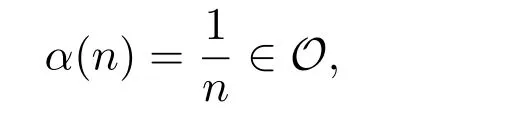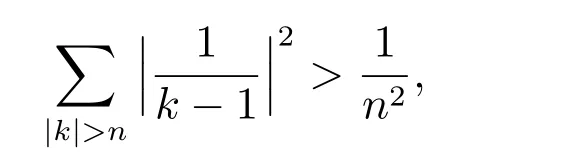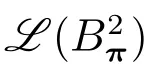过采样技术下Shannon采样重构的任意慢收敛
武 瑛, 高萌瑶, 张雪林
(1-西安科技大学理学院,西安 7 10054;2-陕西师范大学数学与统计学院,西安 7 10062)
1 引言
Shannon采样定理是信号重构理论的基础,并已成为通信工程和信息论中最重要的数学技术之一.与此同时该定理也渗透了许多物理和工程分支,如信号分析、图像处理、雷达、声纳、声学、光学、全息、气象学、海洋学、晶体学、物理化学、医学成像等等[1].该定理具有悠久的研究历史,曾被多位学者独立研究发现.最早于1915年由Whittake在数学文献中做出阐述[2],而后Kotel’nikov于1933年在工程文献上发表了采样定理的相关文章[3].1948年Shannon利用采样定理证明了模拟带限信号在信息意义上等价于其按Nyquist速率采集的样本级数[4].因此,它也被称为Nyuist-Shannon采样定理和Whittaker-Kotel’nikov-Shannon采样定理,并作为插值理论中的基本定理.Shannon采样定理阐述了用离散样本重构连续信号的方法,具体来说它主要分析了两个问题:第一,哪类具有有限能量的连续时间信号,可以通过仅使用等距离采样来做出唯一地表示;第二,如何进行重构.关于更详尽的相关解释建议参考文献[5].在数学上,这个定理描述如下.
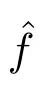

其中

前人已经对(1)中主级数的收敛速率进行了广泛研究.原始的研究致力于采样定理在每一个点t∈R处的点点收敛,并证明了该主级数在R的每一个紧支集上是一致收敛的.此外,文献[6]证明了主级数依L2范数收敛到信号f,即

在p=2时成立.当1 理论上来说,要得到精确的重构就需要无限多的样本.然而在实际应用中,只能获得有限个样本,这也就势必造成了所谓的截断误差.一般地,信号f的n阶截断误差定义为 其中Sn是n阶有限维重构算子,定义为 截断误差可以根据采样率和范数来估计,然而这些估计总是需要某些函数类内信号的先验界,并且一般不适用于带限信号.因此,尽管可以得到某些信号的收敛速率,但是对于所有带限信号,其收敛速率慢的程度依然无从估计. 众所周知,过采样可以加速重构序列的收敛.具体来说,过采样是对[−πW,πW]上的带限信号采用更高的采样率˜W>W来采取样本.在文献[9]中,作者证明了用过采样技术后,对于p=∞,(2)式全局一致收敛.然而,对于一般的带限信号,收敛速率依然是未知的.在文献[10]中,作者证明了应用过采样并认真选择重构基底函数后,在局部有界区间上收敛速度能够达到指数收敛.这也为实际应用中只能选取有限个样本的情况提供了更好的重构方法. 正是由于重构收敛速率的慢,和对于所有带限信号而言的收敛速率有多慢的未知性,在一定程度上影响了采样重构理论的实际应用.因此,研究重建的收敛速度有多慢,在理论上是有意义的.此外,在文献[11]中讨论了收敛速率有多慢,并且遗留了关于加速技术下的重建算子序列是否仍然是“任意慢”的问题.根据于本文的研究成果,也对上述遗留问题做出了回答,即加速技术并没有为慢收敛带来改善. 在本文中,作者应用算子列的慢收敛理论,从重构算子序列Sn的角度来分析香农重构的收敛速率.文章的主要结论见第3节,作者证明了重构算子序列Sn“任意慢”地收敛到恒等算子.具体来说,当1 设Lp(R),1≤p<∞,是所有R上p次幂Lebesgue可积信号的函数空间,其中Lp定义为 对于σ>0,Bσ是所有复平面C上整函数的函数空间,其整函数需满足如下性质:对任意的ε>0,存在一个常数C(ε),使得 文献[12,13]中Banach空间的算子序列慢收敛理论,提供了描叙线性算子序列强收敛的定量方法.令O是收敛到0的所有递减正序列的集合,即 X和Y是同一个标量域上的两个赋范线性空间,且将L(X,Y)定义为所有从X到Y的有界线性算子构成的赋范线性空间.当X=Y时,L(X,Y)简化为L(X).对于序列{Ln}⊂L(X,Y),该序列强收敛到L∈L(X,Y),即 文献[12]中给出任意慢收敛的定义如下. 定义1 对于任意α∈O,若存在x=xα∈X,使得 ‖Ln x−Lx‖Y≥α(n),∀n∈N, 则称序列{Ln}任意慢收敛到L. 以下两个定理是本文所用到的结果.其中定理2意味着满足一定条件时,一个强收敛到恒等算子的有界线性算子序列实际上是任意慢收敛的.定理3是对经典Bernstein嗜睡定理的概括,它为后续任意慢收敛的证明提供了启发和理论支撑.我们先列出定理[14,15]. 定理2 设Fn是从Banach空间X到它自身的映射序列,且使得 则有下列叙述等价: 1)Fn强收敛到恒等算子I; 2)Fn任意慢收敛到恒等算子I; 3)Fn几乎任意慢收敛到恒等算子I. 定理3 设{0}=L0⊂L1⊂L2···是Banach空间X的有限维闭子空间序列,Y是X的无限维闭子空间.那么对于任意α∈O,存在y∗∈Y,使得 下述定理说明了重构算子序列{Sn}在奈奎斯特速率下的收敛速度. 证明 由Sn的定义可知,对任意的n∈N,Sn都是有限维的,即 故根据已知等式(8)和定理2可知,Sn强收敛到恒等算子I且Sn任意慢地收敛到恒等算子I. 其中 W3=W2+δ>W2>W1. 下述定理也是本节内容的主要结果之一. 为了证明定理6,我们需要来自文献[17]中的引理如下. 由引理1,我们有 根据(11)和(12)式可得,对于任意m,有 于是,由(15)和(16)式,可得 因为m=k时sinc(m−k)=1,m̸=k时sinc(m−k)=0,所以(17)式右边的双求和可简化为对满足m=k的m和k求和,这里使用k作为求和指标,我们有 再次利用引理1,级数 是收敛的,即意味着随着n→0, 其中C仅依赖于p和W.我们可以构造出信号f使得该信号满足 即说明奈奎斯特速率下重构算子序列是任意慢收敛的.以p=2为例,对收敛速度很慢的 构造信号f为 ε=(c−∞,···,c−1,c0,c1,···,c∞), 其中 该数列ε的余项收敛到0也是任意慢的.

2 预备知识

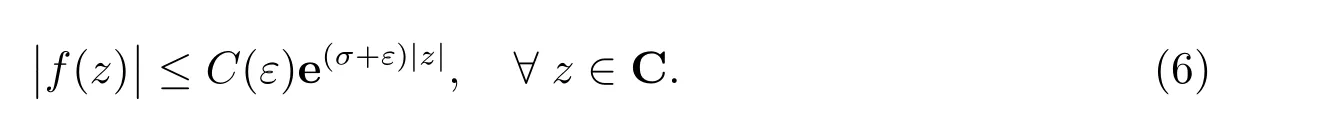




3 重构算子序列的收敛速度
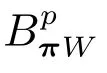


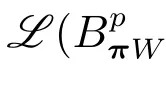
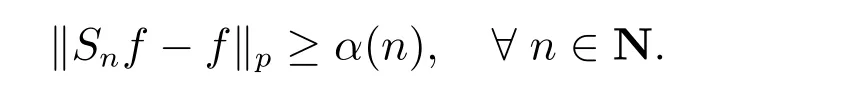
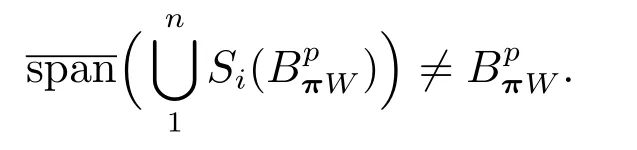



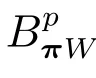
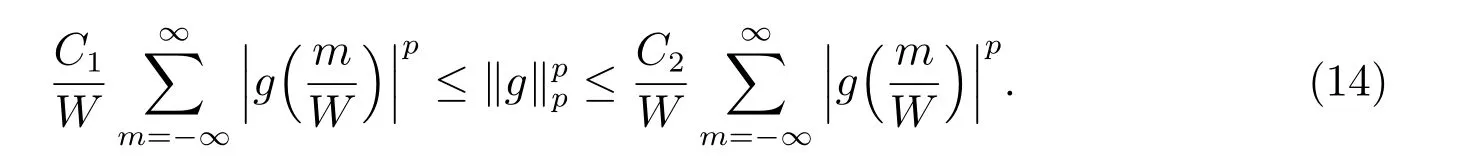
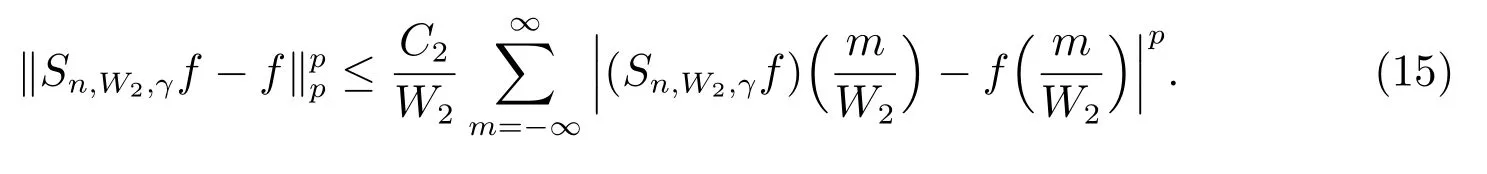





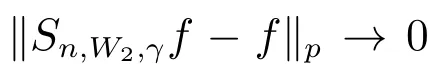


4 结论与应用