多决策覆盖信息系统的约简
许丽婷 李进金† 林艺东 李怡靓
(1-闽南师范大学数学与统计学院,漳州 3 63000;2-福建省粒计算及其应用重点实验室,漳州 3 63000)
1 引言
粗糙集理论[1-3]作为一种处理不精确、不一致、不完整等各类不完备信息的有效工具,由波兰科学家Pawlak在1982年创立.粗糙集理论是一种天然的数据挖掘或者知识发现方法,它与概率论[4]、模糊理论[5]、证据理论[6-8]等领域都有相关的结合.
覆盖粗糙集理论为经典粗糙集的一种推广,其约简理论一直受到广泛的关注.Zhu[9]对覆盖提出了一种约简方法,该约简是产生相同覆盖上、下近似的最小覆盖,为数据挖掘中消除冗余提供了一种有效技术.覆盖信息系统可以进一步的推广到覆盖决策信息系统,其中用划分刻画决策属性的覆盖决策信息系统的约简理论的研究十分广泛.夏秀云等[10]利用信息熵,讨论协调覆盖决策系统的相关约简.辨识矩阵是覆盖决策信息系统约简理论的一个重要的工具.Chen等[11]在决策为划分的覆盖决策信息系统中提出了一种减少覆盖决策系统属性的方法.由于决策为划分有一定的局限性,因此一些学者将决策从划分推广为覆盖,然后再对覆盖决策信息系统的约简理论进行研究.张燕兰和李进金[12]在文献[11]的基础上研究了在决策为覆盖的覆盖决策信息系统中保持正域不变的相对约简,并通过构造辨识矩阵求其约简.Zhang和Li[13]介绍了一族覆盖的两种相对约简,并且通过构造了两个辨识矩阵研究所有相对约简的结构.然而在根据辨识矩阵求其约简的过程中,由于辨识矩阵过于复杂,而导致计算过程中时间复杂度为指数级.在数据集相对较大时难以计算.本文通过将决策为覆盖的覆盖决策信息系统转化为多决策覆盖信息系统,提出了两类新约简,并将此系统下的两类约简与文献[13]下的约简方法进行比较.
本文通过特征函数将覆盖决策信息系统转化为多决策覆盖信息系统.首先,在多决策覆盖信息系统下定义了两类协调集,构造了两个辨识矩阵,通过这两个辨识矩阵研究多决策覆盖信息系统的约简问题,讨论多决策覆盖信息系统中的两类协调集与覆盖决策信息系统中的上近似协调集之间的联系.
2 预备知识
在采集数据的过程中,可能由于条件不够等原因使得一些对象的决策缺失或者不能完全确定,这时若将决策刻画为划分,则会导致数据部分失真,故在一些决策信息系统中的决策属性以覆盖刻画更恰当,下面将给出例子进行解释说明.
例1 若某企业想要判断每项技术的成熟性,为了对技术进行创新决策.设决策信息系统为(U,A,F,d),U表示每项技术的集合,共有5项技术待评估.A={a1,a2}表示影响各项技术成熟程度的属性,a1表示市场需求的情况,a2表示需求变化的情况.F={f1:U→Vl(al∈A)}为每项技术和各个属性的关系,即每项技术在各个属性下的取值,Vl为属性al的值域.d:U→Vd表示技术的成熟程度,Vd为属性d的值域.如表1所示,有一个连续值决策信息系统,其条件属性和决策属性的取值范围在[0,4]内.
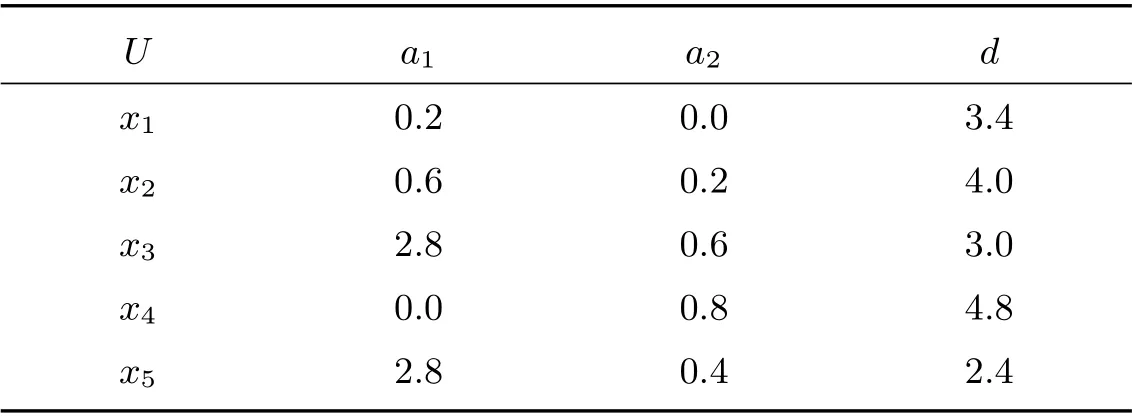
表1 例1中的决策信息系统
对任意B⊆A,d,定义RB,Rd如下
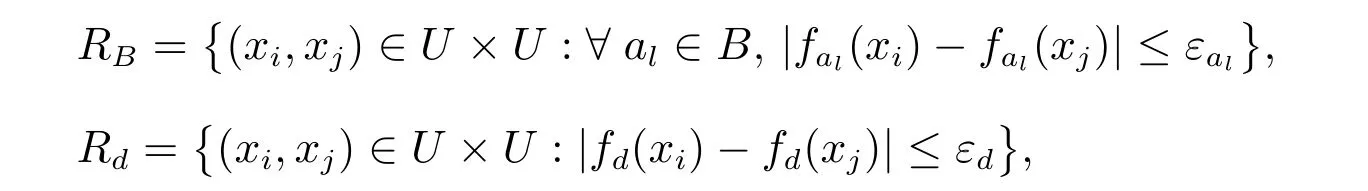
其中εal>0,εd>0,显然RB,Rd满足自反、对称,但一般不满足传递.因此
Ci={(Rai)s(x)|x∈U},i=1,2,Cd={(Rd)s(x)|x∈U}
为覆盖.
若εa1=0.4,εa2=0.2,εd=1.2,则可得到三个覆盖为
C1={{x1,x2,x6},{x1,x2},{x3,x5},{x1,x4}},
C2={{x1,x2,x5},{x1,x2,x3,x5},{x3,x4,x5},{x3,x4},{x2,x3,x5}},
Cd={{x1,x2,x3,x5},{x1,x2,x3,x4},{x1,x3,x5},{x2,x4}}.
例2 如表2所示,给出了一个不完备决策信息系统I=(U,A,F,d),其中对象集为U,属性集为A,F={f1:U→Vl(al∈A)}代表对象和属性的关系集,Vl为属性al的值域,d:U→Vd,其中Vd取有限值.
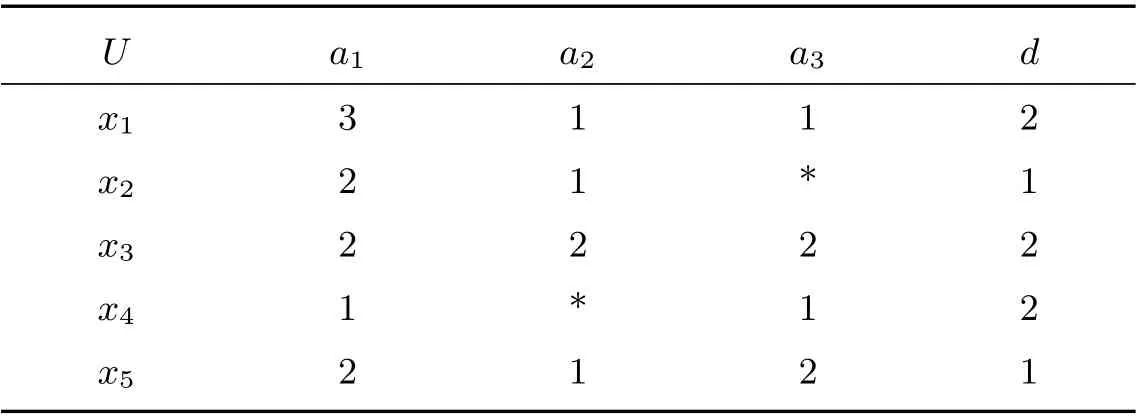
表2 例2中的不完备决策信息系统
对于B⊆A,定义如下优势关系
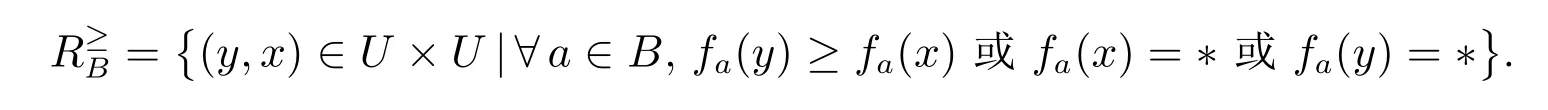
设I=(U,A,F,d)为不完备决策信息系统,对于决策d,U可以被划分为有序的类
D={Dt,t∈T},T={1,2,···,k}.
对于任意r,s∈T,若r>s,则代表Dr中的元素优于Ds中的元素,因此,这些有序的决策类可以分别使用向上联合和向下联合近似来表示,有
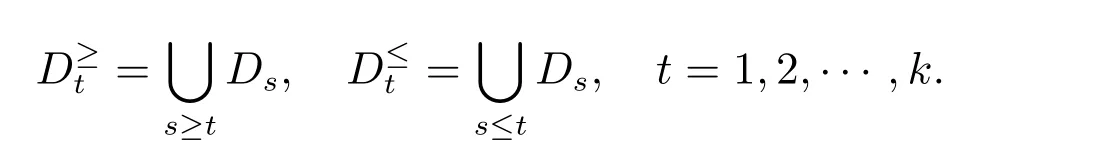
由表2可得
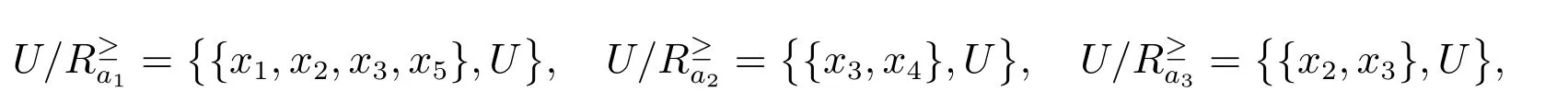
决策类为D={D1,D2},其中D1={x2,x5},D2={x1,x3,x4}.由于2>1,因此D2中的对象比D1中的对象优,根据向上联合近似的定义可以得到
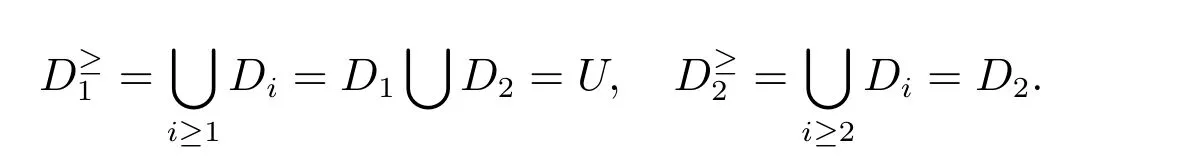

例1和例2表明在一些决策信息系统中,利用覆盖刻画其条件属性与决策属性更具有合理性,故研究以覆盖刻画其决策的覆盖决策信息系统的属性约简问题具有理论与实践意义.以下给出了覆盖决策信息系统的相关知识,其决策以覆盖刻画.
定义1[11]设A={Cj|j=1,2,···,n}为U上的一族覆盖,对任意x∈U,则x在覆盖A下的邻域定义为
(x)A=∩{K|x∈K,K∈Cj,j=1,2,···,n}.
A诱导的U上的一个覆盖为
cov(A)={(x)A|x∈U}.
对任意B⊆A,x,y∈U,有如下性质:
1)y∈(x)B⇔(y)B⊆(x)B;
2) (x)B=∩C∈B(x)C;
3) (x)A⊆(x)B,(x)B=(x)cov(B).
根据定义1,可得一对关于覆盖cov(A)的近似算子.
定义2[9]设A={Cj|j=1,2,···,n}为U上的一族覆盖,对任意X⊆U,X关于cov(A)的上近似算子定义为

易得它的对偶下近似算子为
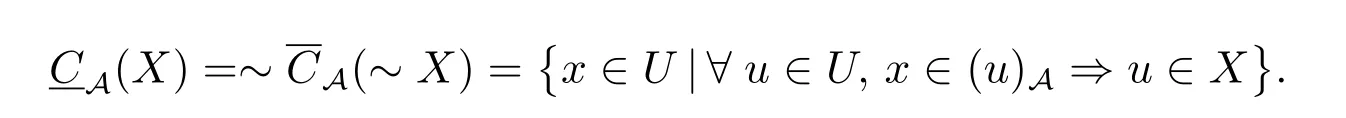
Zhang和Li[13]给出了有关保持上下近似算子不变的约简理论以及辨识矩阵.
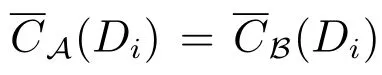
定义4[13]设(U,A,CD)是覆盖决策信息系统,对x,y∈U且有Di∈CD,记
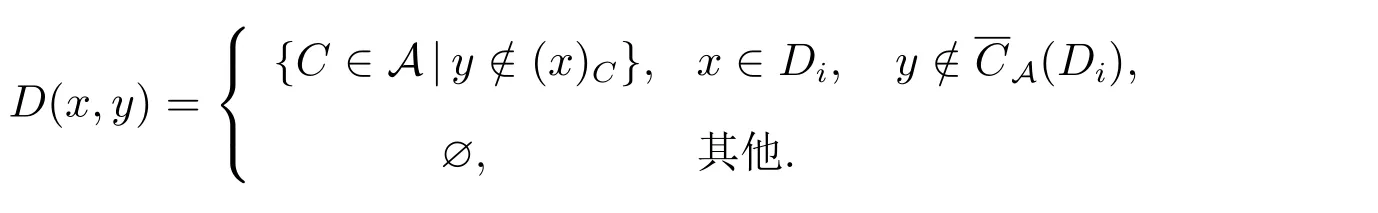
称D(x,y)为x对y的上近似辨识集,则D={D(x,y)|x,y∈U}为x对y的上近似辨识矩阵.
引理1[13]设(U,A,CD)是覆盖决策信息系统,B是A的上近似协调集,当且仅当D(x,y)̸=∅时,B∩D(x,y)̸=∅.
引理2[6]设C是A的上近似核心,且C∈A,当且仅当存在x,y∈U,使得D(x,y)={C}.
例3 设论域U={1,2,3,4,5},U的一族覆盖为A={C1,C2,C3},CD为U的一个覆盖,且
C1={{1,2,4},{2,3,5},{1,5}},C2={{1,3,4},{2,5},{4,5}},
C3={{1,4,5},{2,4},{3,5}},CD={{1,3},{2,4,5},{1,3,4},{2,5}}.
易得表3.

表3 例3中各点的邻域
由表3可以得出
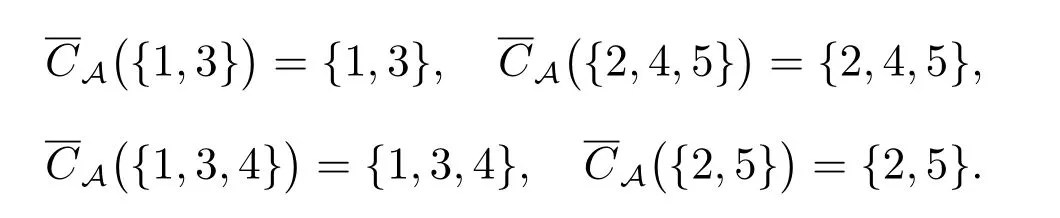
从而上近似辨识矩阵为
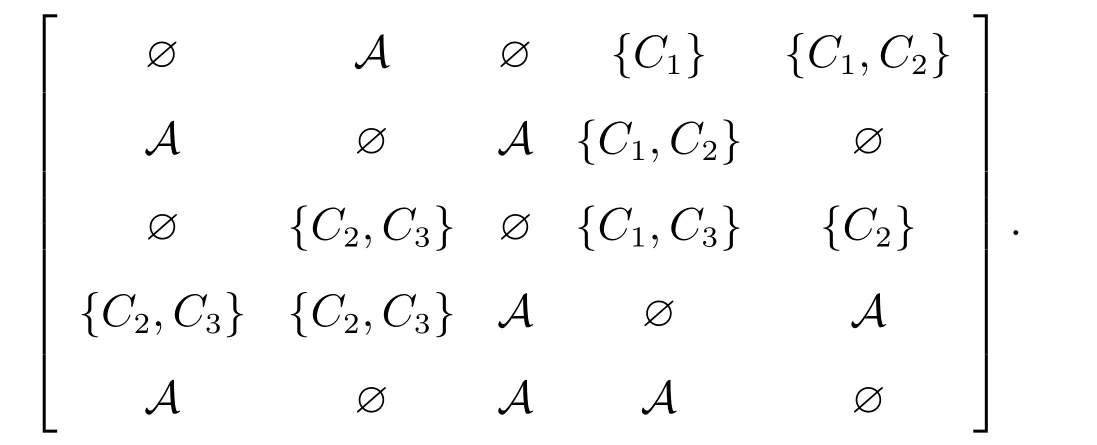
根据引理1知,B={C1,C2}是上近似协调集,但B1={C1}和B2={C2}都不是上近似协调集,所以B={C1,C2}是上近似约简集.
3 基于多决策覆盖信息系统type-1辨识矩阵的约简
首先,给出特征函数的定义,而后通过特征函数将覆盖决策信息系统中以覆盖刻画的决策转化为一个形式背景,从而产生多决策覆盖信息系统.
定义5 设(U,A,CD)是覆盖决策信息系统,CD={D1,D2,···,Dn}是U上的一个覆盖,特征函数定义为
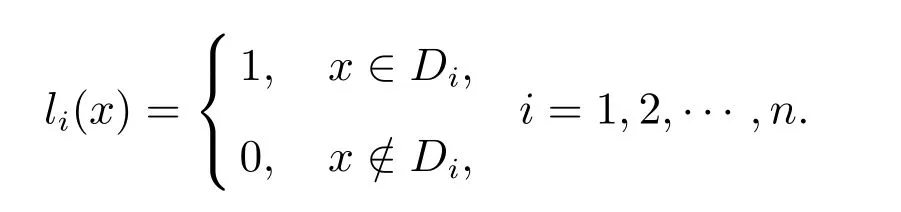
定义6 设(U,A,CD)是覆盖决策信息系统,其中A为U上的一族覆盖,CD={D1,D2,···,Dn}为U上的一个覆盖,LD={l1,l2,···,ln},其中li:U→{0,1},i=1,2,···,n,则称(U,A,LD)为多决策覆盖信息系统.
对于多决策覆盖信息系统定义一个U上的等价关系如下.
定义7 设(U,A,LD)是多决策覆盖信息系,对x,y∈U,有
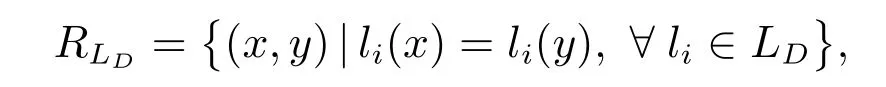
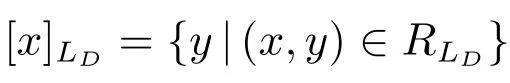
当LD={li}时,有
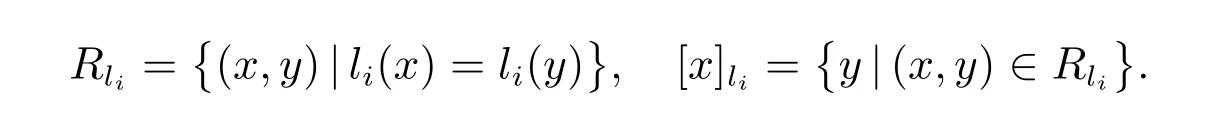
下面给出关于多决策信息系统type-1覆盖协调集和type-1覆盖约简集的判定定理.
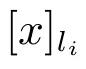
定理1 设(U,A,CD)是覆盖决策信息系统,(U,A,LD)是多决策覆盖信息系统,若B为覆盖信息系统的上近似协调集,则B为多决策覆盖信息系统的type-1覆盖协调集.
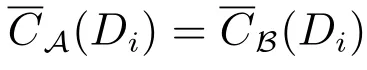
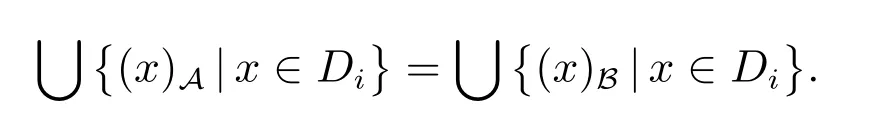
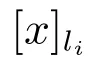
然而,反之不一定成立,下面举例说明.
例4 设论域U={1,2,3,4,5},U的一族覆盖为A={C1,C2,C3},CD为的一个覆盖,且C1={{1,2},{2,3,4},{4,5}},C2={{1,2,3},{3,4},{5}},C3={{1,2},{3,4},{4,5}}.
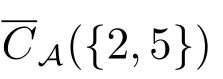
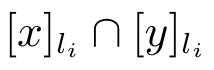
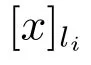
我们可以通过构造辨识矩阵来描述覆盖协调集和覆盖约简集.首先,针对type-1覆盖协调集和type-1覆盖约简集构造对应的type-1多决策覆盖辨识集并给出相关定理.
定义9 设(U,A,LD)是多决策覆盖信息系统,对x,y∈U,存在li∈LD,记
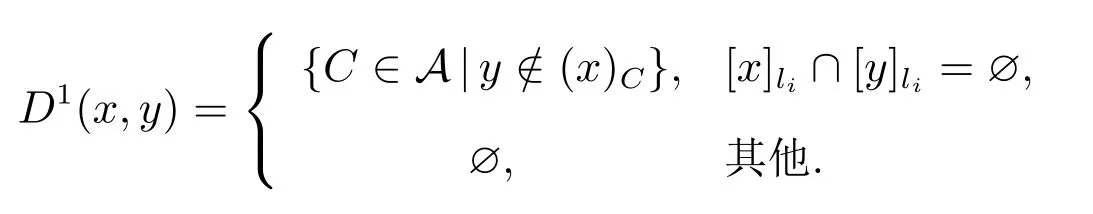
称D1(x,y)为x对y的type-1多决策覆盖辨识集,则D1={D1(x,y)|x,y∈U}为x对y的type-1多决策覆盖辨识矩阵.
下面通过构造的type-1多决策覆盖辨识集和type-1多决策覆盖辨识矩阵来判定type-1覆盖协调集和type-1覆盖约简集.
定理3 设(U,A,LD)是多决策覆盖信息系统,B是type-1覆盖协调集,当且仅当D1(x,y)̸=∅时,B∩D1(x,y)̸=∅.
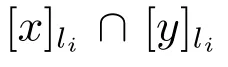

例5 续例3,由覆盖CD={{1,3},{2,4,5},{1,3,4},{2,5}},可以得到如表4的一个形式背景.

表4 例5中x与li的关系
由表4可知产生的等价类为
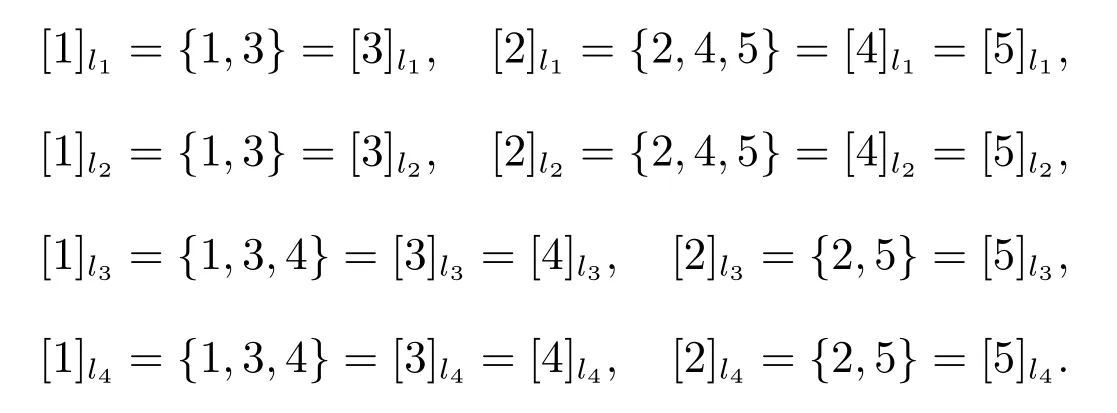
从而可得一个type-1多决策覆盖辨识矩阵

根据定理3知,B={C1,C2}是type-1覆盖协调集,但B1={C1}和B2={C2}都不是type-1覆盖协调集,所以B={C1,C2}是type-1覆盖约简集.
对于例3,在多决策覆盖信息系统下求出的约简与覆盖决策信息系统的结果相同.在计算辨识矩阵的过程中,由于文献[13]在计算辨识矩阵时需要计算的是上近似,而本文只需计算等价类,所以此方法比文献[13]中的方法简便,且计算量小,节省时间.
在计算出type-1多决策覆盖辨识矩阵之后,我们不仅可以通过定理3得出type-1覆盖协调集和type-1覆盖约简集,还可以通过以下区分函数来求得多决策覆盖信息系统的约简集.
定义10 设(U,A,LD)是多决策覆盖信息系统,D1={D1(x,y)|x,y∈U}为type-1多决策覆盖辨识矩阵,记
M=∧{∨{C|C∈D1(x,y)}|x,y∈U},
M称为覆盖区分函数,其中∧表示(合取)运算,∨表示(析取)运算.
由定义10,可以得到如下定理.
定理4 设(U,A,LD)是多决策覆盖信息系统,D1={D1(x,y)|x,y∈U}为type-1多决策覆盖辨识矩阵,覆盖区分函数M的最小析取范式是
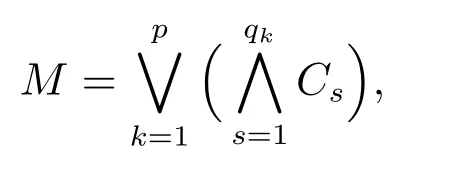
其中Bk={Cs|s=1,2,···,qk},{Bk|k=1,2,···,p}是type-1覆盖约简集.
例6 续例5,利用区分函数有
M=C1∧(C2∨C3)∧(C1∨C3)∧(C1∨C2∨C3)∧(C1∨C2)∧C2=C1∧C2.
所以B={C1,C2}是type-1覆盖约简集.
将多决策覆盖信息系统中的覆盖分类后,便于研究不同覆盖各自的特征.下面给出覆盖分类及判别方法.
定义11 设(U,A,LD)是多决策覆盖信息系统,Bk(k≤r)为所有覆盖约简集,记
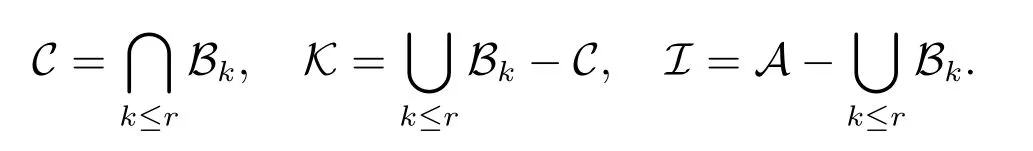
Ci∈C时,称Ci为核心覆盖,C称为核心覆盖集;Ci∈K时,称Ci为相对必要覆盖,K称为相对必要覆盖集;Ci∈I时,称Ci为不必要覆盖,I称为不必要覆盖集.
定理5 设(U,A,LD)是多决策覆盖信息系统,则下列命题等价:
1)C′是核心覆盖;
2) 存在x,y∈U,D1(x,y)={C′};

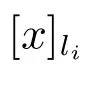
3) 若C′为不必要覆盖⇔存在li∈LD,使得(x)(C′)⊆[x]li∪(x)C′.
4 基于多决策覆盖信息系统type-2辨识矩阵的约简
下面给出另一类多决策覆盖辨识矩阵来判定覆盖协调集和覆盖约简集.

由定理1上近似协调集是type-1覆盖协调集可类似的推出上近似协调集是type-2覆盖协调集.
定理8 设(U,A,CD)是覆盖决策信息系统,(U,A,LD)是多决策覆盖信息系统,若B为覆盖信息系统的上近似协调集,则B为覆盖信息系统(U,A,CD)的上近似协调集,当且仅当B为多决策覆盖信息系统(U,A,LD)的type-2覆盖协调集.
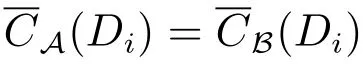
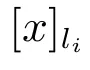
定理9 设(U,A,LD)多决策覆盖信息系统,若B为type-2覆盖协调集,则B为type-1覆盖协调集.
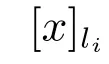
反之,不一定成立,下面举例说明.
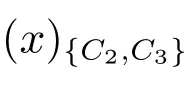
类似定理2,可以得到如下定理,根据此定理构造type-2多决策覆盖辨识集.
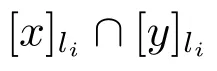
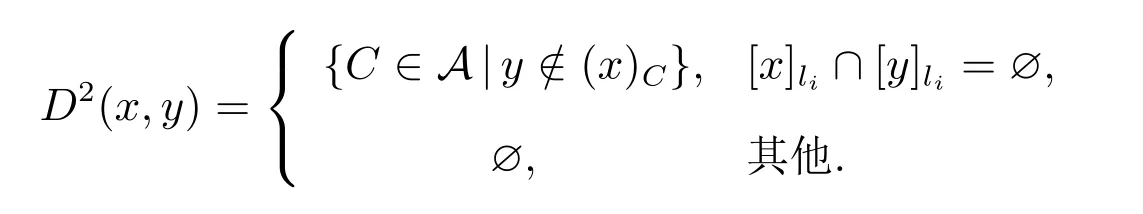
定义13 设(U,A,LD)是多决策覆盖信息系统,对x,y∈U,任意li∈LD,记称D2(x,y)为x对y的type-2多决策覆盖辨识集,则D2={D2(x,y)|x,y∈U}为x对y的type-2多决策覆盖辨识矩阵.
通过上述构造的type-2多决策覆盖辨识集和type-2多决策覆盖辨识矩阵给出相关的type-2覆盖协调集和type-2覆盖约简集的定理.
根据定理3中type-1覆盖协调集的充要条件,类似的可以得出type-2覆盖协调集的充要条件.
定理11 设(U,A,LD)是多决策覆盖信息系统,B是type-2覆盖协调集,当且仅当D2(x,y)̸=∅时,B∩D2(x,y)̸=∅.
例8 由例5的等价类可得一个type-2多决策覆盖辨识矩阵
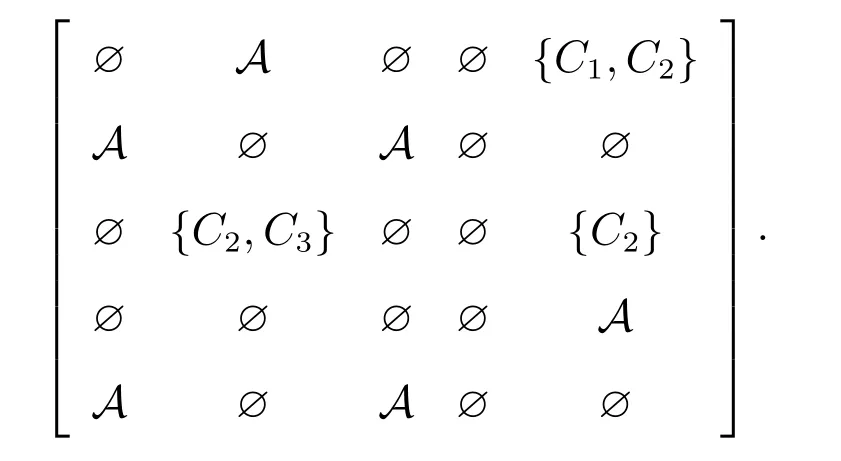
根据定理11知B={C2}是type-2覆盖约简集.
从例8可以看出,type-2多决策覆盖辨识矩阵求出的约简集与type-1多决策覆盖辨识矩阵有所不同.由于type-1多决策覆盖辨识矩阵中的非空集合比type-2多决策辨识矩阵中的非空集合多,因此,在利用区分函数来计算约简集时tpye-2比type-1计算量小.
对于type-2多决策覆盖辨识矩阵,也有类似于定义10的覆盖区分函数
M=∧{∨{C|C∈D2(x,y)}|x,y∈U}.
在type-2多决策覆盖辨识集下也有相关覆盖分类的判别方法.
根据定理5,可以类似给出type-2多决策覆盖辨识集下核心覆盖的等价条件.
定理12 设(U,A,LD)是多决策覆盖信息系统,则下列命题等价:
1)C′′是核心覆盖;
2) 存在x,y∈U,D2(x,y)={C′′};
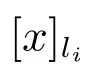
由定理6,同理可以给出type-2多决策覆盖辨识集下不必要覆盖的等价条件.

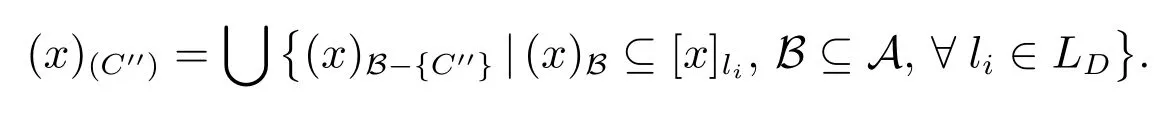
结合定理12与定理13,得出相对必要覆盖的充要条件.
定理14 设(U,A,LD)是多决策覆盖信息系统,则有以下结论:
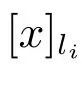
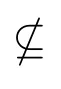
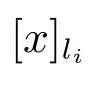
5 结束语
本文将覆盖决策信息系统中以覆盖刻画的决策通过特征函数转化为由0和1组成的形式背景,给出了多决策覆盖信息系统的定义,进而研究在多决策覆盖信息系统下的约简.在多决策覆盖信息系统中提出两类协调集判定方法,构造了两个相应的辨识集,进一步讨论多决策覆盖信息系统中的两类协调集与覆盖决策信息系统的协调集之间的关系.
对于本文给出的两类多决策覆盖辨识矩阵,计算量相对较小,可以节省求解覆盖约简的时间,在实际应用中具有一定的意义.此外,还可以继续讨论三个辨识矩阵之间的关系,以及三个辨识矩阵所产生的约简集之间的联系.

