基于频域方法的制动夹钳振动疲劳失效预测

曾梁彬，吕 斐，赵金良

（中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213011）

0 引言

制动夹钳单元是轨道交通车辆基础制动装置中的核心执行部件，尤其在列车紧急制动、停车制动和驻车制动等过程中承担着主要功能，是保障列车行车安全的重要环节[1-2]。

在车辆运行过程中，一方面当轨道不平顺、通过曲线、道岔和会车时，会引起车辆转向架、车体的受激振动；另一方面，由于摩擦材料不是完全刚性，在制动过程中摩擦副表面存在一定的粘滑现象，导致制动盘和闸片之间摩擦力不断变化并引发制动部件的自激振动[3-6]。由此可以看出，制动夹钳单元在现车服役过程中长期处于振动激励状态，尤其是线路因素和制动过程引起的随机振动，对夹钳的结构强度和疲劳寿命存在较大的影响。

为适应轨道交通高速化和绿色化的发展趋势，轻量化成为制动夹钳单元等转向架安装设备在当前的一个主要技术发展特征。然而，轻量化必然会对产品结构强度和可靠性带来影响[7]。因此，开展制动夹钳单元随机振动工况下的疲劳失效模式与寿命预测研究显得十分重要。

目前行业内针对制动夹钳单元产品的结构强度计算，多以传统静态分析方法为主[8-10]，疲劳分析一般也是通过静态工况下获得的应力结果，结合Miner 线性累积损伤理论对疲劳损伤进行评估。由于静态分析中无法考虑结构的动态特性，应力响应分析与损伤计算结果往往并不准确[11]。为更加准确地研究制动夹钳单元在实际振动服役工况下的失效模式与结构强度，动态疲劳分析就显得十分必要。

在工程实际中，结构动态疲劳分析方法主要包括时域法和频域法两类。时域法能够获取载荷及响应的历程特征，并且可以处理非高斯随机工况，通常具有较高的分析计算精度；但其需要收集庞大的载荷信号的数据样本，计算工作量较大。而频域法针对高斯分布的随机振动工况，利用功率谱密度函数描述振动输入信号，可以更加方便的包含随机过程的大多数统计信息，并通过零件关键部位的应力功率谱密度来预测结构疲劳损伤，大大提高了计算效率[12-13]。制动夹钳单元作为转向架安装设备，大部分服役条件下所受到的载荷激励可视为随机振动；因此，采用频域法对其振动疲劳损伤过程进行分析更加具有工程应用推广价值。

1 随机振动疲劳损伤分析方法

1.1 应力响应功率谱密度分析

随机过程是取值为随机变量的时变函数，描述随机变量统计特性的方法和计算公式可以推广到随机过程中[14]。随机过程一般可分为平稳随机过程和非平稳随机过程，若随机过程的所有均方根值和高阶矩不随时间变化则可视为平稳过程。根据IEC 61373—2010，制动夹钳单元在服役工况下的随机振动一般可视为平稳随机过程，即服从高斯分布特点[15]；因此，可以采用功率谱密度（PSD）对载荷的能量分布在频域内进行描述。

为便于工程实现，对于已知随机振动载荷功率谱的情况，可以利用有限元软件对目标结构进行频率响应分析，确定目标对象结构薄弱环节，并获得其应力响应功率谱密度函数G(f)。

根据功率谱密度形状的不同，平稳过程有可大致分为窄带过程和宽带过程。定义不规则因子γ 为：

其中，mi为应力响应功率谱密度函数G(f)的i阶谱矩，其定义为：

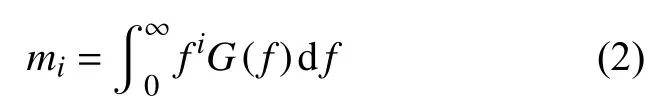
当 γ趋近于1 时，随机过程近似于单一频率的窄带谐波信号；当 γ趋近于0 时，随机过程近似于宽带白噪声信号。

与不规则因子 γ类似的，工程中经常采用带宽系数ε来描述随机过程的带宽，ε定义如下：

此外，根据应力响应功率谱密度函数G(f)还可以进一步计算出单位时间内正斜率穿越零值次数的数学期望E0和单位时间出现峰值次数的数学期望EP，其计算公式为：

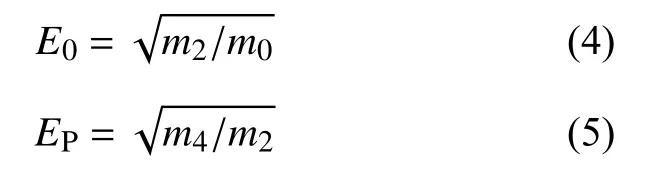
1.2 应力幅值概率密度分析

由于频域方法并不能直接反映应力幅值的加载历程，还需要将应力功率谱密度函数G(f)进一步转化为应力幅值概率密度（PFD）函数P(S)[16]。

1）应力幅值分布规律。

文献[12]、文献[16]中针对常见的几种随机过程应力幅值分布模型进行了比较。结论认为，Bendat[17]提出采用Rayleigh 分布模型适用于窄带随机过程的描述，而Dirlik[18]提出的利用2 个Rayleigh 分布和1 个指数分布的组合模型更加适用于宽带随机过程。文献[16]特别指出，对于带宽系数ε＜0.3 的情况，宜采用Rayleigh 分布模型；带宽系数ε＞0.5 的情况，宜采用Dirlik 分布模型。

Bendat 提出的Rayleigh 分布模型为：

2）“三区间”模型。

文献[7]中介绍了Steinberg 提出的一种基于高斯分布的应力幅值概率分布模型。假设应力变程S也服从高斯分布规律；因此，其概率密度函数P(S)可表达为：

其中：为S的平均值；σ为应力均方根值。

在平稳随机过程中，瞬时值S在±1σ范围内的概率为68.26%；在1σ～2σ和-2σ～-1σ范围内的概率为27.18%；在2σ～3σ和-3σ～-2σ范围内的概率为4.30%；应力幅超过3σ的情况视为小概率事件，假定不发生也不产生结构损伤。

该方法将整个随机过程的应力幅值分布离散为3 个区间，每个分布区间对应着一个固定的应力幅值水平，利用高斯分布的概率密度函数可对各应力水平的出现概率进行简化近似评估，这为工程应用提供了一种简便的评估手段。

1.3 疲劳累计损伤评估

无论采用何种分布模型，当获得应力幅值概率密度函数P(S)后，可进一步基于Miner 线性累计损伤理论对随机过程的总损伤进行评估。

将随机过程中的应力水平离散为若干个区间（Si，Si+ΔS），其在时间T内的循环次数ni以及累计损伤Di为：

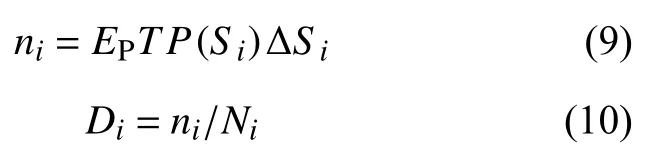
其中，Ni为应力水平Si对应的结构疲劳寿命。整个随机过程各级应力水平产生的总损伤D为：

若D＞1，则认为结构发生疲劳失效。

2 制动夹钳结构疲劳损伤分析

以3 点吊挂制动夹钳为例，利用上述介绍的Rayleigh 模型、Dirlik 模型和“三区间”模型对其关键结构件随机振动工况下的疲劳损伤进行对比分析，比较3 种频域计算方法的分析结果差异。

2.1 制动夹钳有限元模型

制动夹钳单元夹钳部分有限元模型见图1。假设制动过程中零部件之间不存在明显刚体运动，并忽略零部件配合中存在的微小间隙，对制动夹钳模型进行线性化处理。约束双侧闸片托横向位移；将与转向架连接的前后吊挂点固定；制动缸简化为2 个惯性质点，分别与两侧杠杆末端上下销孔耦合，并设置2 个质点之间的轴向刚度；闸片托与大地之间设置纵向与垂向的弹性连接；对存在转动配合的零件之间采用转动副或铰链连接。模型中各主要零件的材料属性与前处理设置详见文献[4]。

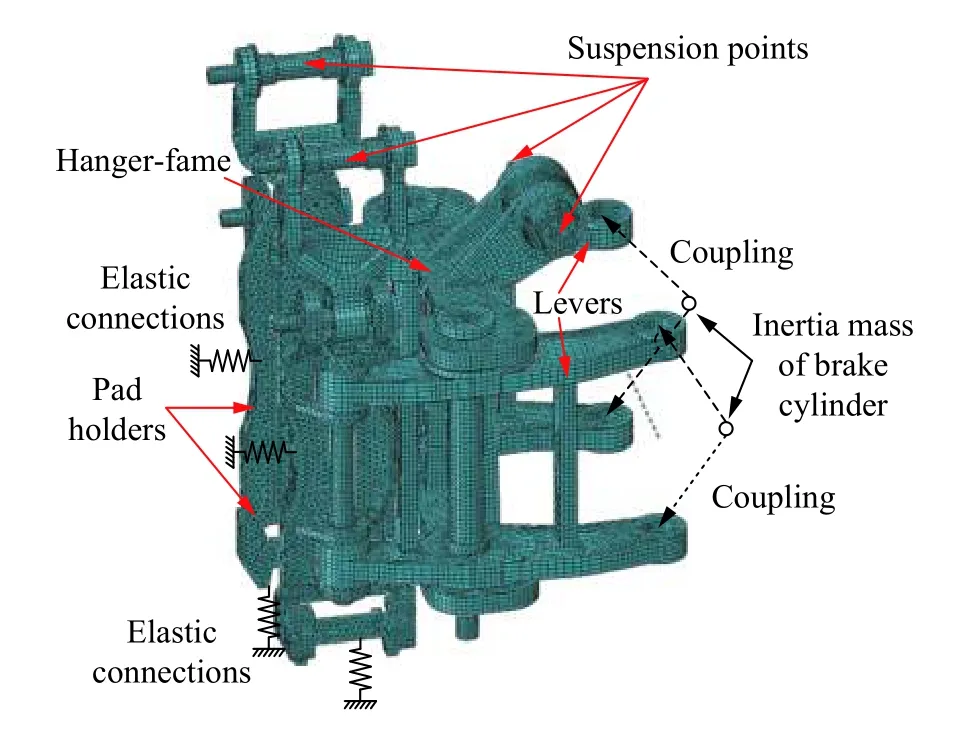
图1 制动夹钳有限元模型Fig.1 FEA model of brake caliper

2.2 模态频响分析

利用有限元方法，对上述制动夹钳的线性模型进行模态分析，获得前30 阶模态振型，通过线性摄动分析中的随机响应分析，计算出制动夹钳在横向、垂向和纵向随机振动工况下应力响应。

随机振动工况参考IEC 61373—2010 中3 类随机振动试验条件执行。值得注意的是，制动夹钳单元属于转向架安装设备，即应以2 类随机振动试验条件对产品性能进行考核[15]。本研究采用3 类试验条件作为激励载荷已超出正常服役性能要求，目的在于加速结构疲劳失效过程。

制动夹钳主要承载零件杠杆、吊座在各向随机振动工况下的RMises 应力响应情况见图2。在横向和垂向随机振动下，杠杆最大RMises 应力出现在后侧垂向筋与上下杠杆臂连接根部，分别达到112.6、144.8 MPa，吊座RMises 应力出现在垂向筋与上梁连接根部，达到77.9、184.6 MPa；在纵向振动下，杠杆最大RMises 应力出现在杠杆臂前端内侧，达到29.9 MPa，吊座RMises 应力出现在颈部筋与上梁连接根部，达到31.4 MPa。

图2 随机振动工况下RMises 应力分布Fig.2 RMises stress distribution under random vibration

进一步，可以获得杠杆和吊座最大RMises 应力处的应力响应功率谱密度曲线（图3）。

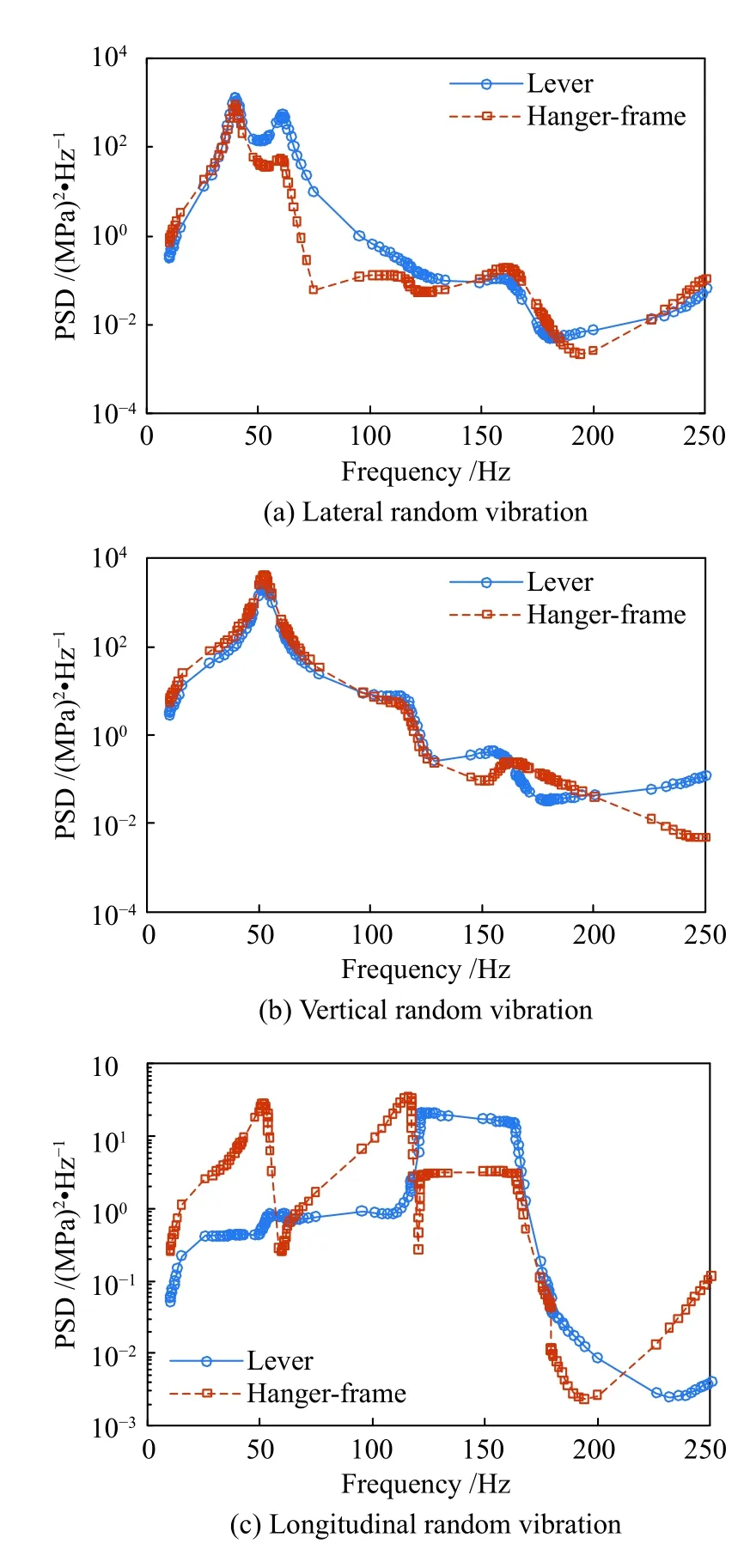
图3 最大RMises 应力位置应力功率谱Fig.3 PSD of maximum RMises stress position

结合应力响应功率谱密度曲线，根据式（1）～式（3），可以计算得到各向随机振动工况下杠杆和吊座最大RMises 应力处应力响应的带宽系数，结果见表1。

表1 应力响应带宽系数Table 1 Bandwidth coefficients of stress response

2.3 疲劳损伤评估

对于一般工程应用，可以用以下幂函数公式来表述金属材料的应力-寿命关系：

其中，m和C为材料疲劳性能相关常数，可以通过试验数据拟合得到。图4 为杠杆、吊座所使用的QT600-7 材料疲劳试验（应力比r=0.5、应力集中系数kt=1）实测数据。通过数据拟合，计算得到m=10.51，C=1.77×1031。

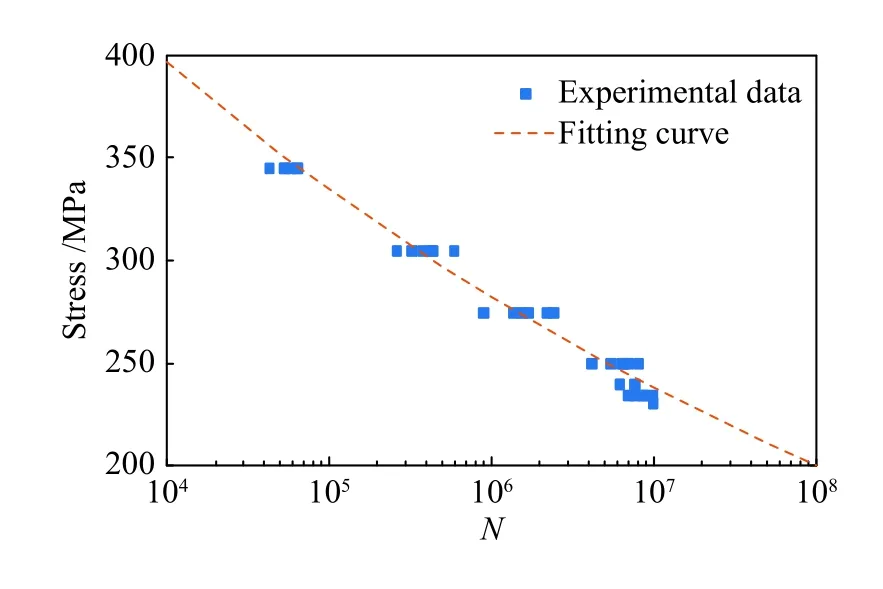
图4 QT600-7 材料S-N 曲线Fig.4 S-N curve of QT600-7

将式（12）代入式（9）～式（10）可以将疲劳总损伤计算公式变形为：

将图3 中通过仿真得到的各向随机振动工况下杠杆和吊座最大RMises 应力位置的应力响应功率谱数据分别代入式（6）和式（7），可以用Rayleigh 模型和Dirlik 模型计算得到相应位置利的应力幅值概率密度曲线（图5）。

图5 最大RMises 应力位置应力幅值概率密度Fig.5 PDFs of maximum RMises stress position

对于采用“三区间”模型（Steinberg 模型）的分析而言，则可进一步得到：

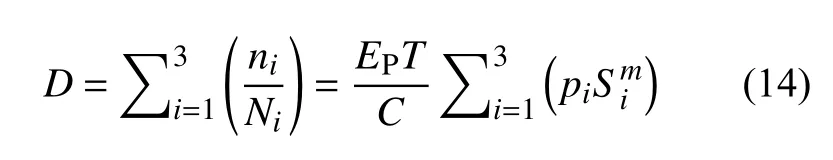
其中，p1=68.26%，p2=27.18%，p3=4.33%。

通过式（13）、式（14），最终可以计算得到制动夹钳杠杆和吊座结构最薄弱位置在各向随机振动工况下的疲劳损伤。考虑到损伤分析结果受应力幅值范围影响较明显，3 种模型的分析中选取相同的应力幅值范围（0～3σ，σ取值见图2）。计算结果见表2。

表2 疲劳累计损伤计算结果（T=0.5 h）Table 2 Fatigue cumulative damage (T=0.5 h)

2.4 结果对比分析

在针对横向和纵向随机振动工况的损伤分析中，3 种模型计算得到的疲劳损伤均小于1，即预测制动夹钳的杠杆和吊座结构未发生失效，其中，纵向振动工况下的疲劳损伤远远低于横向振动工况。在针对垂向随机振动工况的损伤分析中，利用Rayleigh 模型计算得到的杠杆疲劳损伤小于1，吊座疲劳损伤大于1，即吊座发生结构失效；利用Dirlik 模型和“三区间”模型计算得到的杠杆和吊座疲劳损伤均大于1，即2 个零件均发生结构失效。由此可以看出，采用Dirlik 模型和“三区间”模型对结构失效的预测结果更为接近。

从3 种模型计算得到的疲劳损伤绝对数值的对比来看，Rayleigh 模型计算得到的疲劳损伤最小，“三区间”模型次之，Dirlik 模型计算得到的疲劳损伤最大。此外，Dirlik 模型和“三区间”模型的计算结果差异相对较小，误差基本在30%以内；而Rayleigh 模型的计算结果与前2 种模型相比则差异较大，相对于Dirlik 模型的计算误差在70%左右。计算误差如表3 所示。

表3 3 种模型计算结果相对误差比较Table 3 Comparison of relative errors obtained by three models %

3 加速失效试验

按照上述分析中的随机振动工况，在振动台上进行3 个振动方向各0.5 h 的加速失效试验。

在横向和纵向试验条件下，制动夹钳样品未发生结构失效。而在进行完垂向试验后，制动夹钳的杠杆和吊座均发生结构失效，其中，杠杆垂向筋与杠杆臂的连接根部、吊座垂向筋与上梁的连接根部产生断裂（图6）。从产生失效的部位来看，实际发生断裂的位置与上述模态频响分析中的最大RMises 应力位置一致，说明该有限元模型的建模线性化处理方式和分析步（模态分析+随机响应分析）的选择较为合理。从失效预测结果来看，3种模型均预测横向与纵向随机振动工况下制动夹钳结构不会产生失效；Dirlik 模型和“三区间”模型预测垂向随机振动工况下杠杆和吊座均将发生失效，而Rayleigh 模型预测结果中仅吊座发生失效。相比之下，前两种模型的预测结果与试验结果更为吻合。

图6 加速失效试验后断口Fig.6 Fractures from accelerated failure test

4 结论

1）借助有限元手段，通过对制动夹钳结构模型进行线性化处理，并采用模态分析和随机响应分析，可以有效确定出随机振动工况下结构设计的相对薄弱环节，同时可以获得应力响应功率谱密度曲线，为疲劳损伤分析提供数据输入。

2）利用Rayleigh 模型、Dirlik 模型和Steinberg的“三区间”模型，结合Miner 线性累计损伤理论，可以对随机振动工况下的疲劳损伤进行估计。其中，Dirlik 模型与“三区间”模型的计算结果更为接近，Rayleigh 模型计算结果则存在较大相对误差。

3）从与加速破坏试验结果的对比情况来看，Dirlik 模型与“三区间”模型与结构疲劳失效的预测相对更为准确。