数据预处理对LSTM网络大气污染预测精度分析∗

杜英魁张乙芳原忠虎关 屏彭 跃

（1.沈阳大学信息工程学院 沈阳110000）（2.沈阳恒源伟业环境检测服务有限公司 沈阳110000）（3.辽宁省环境监测实验中心 沈阳110000）

1 引言

随着经济的快速发展，大气污染也逐日严重。沈阳作为东北老工业的重点城市，大气环境质量也不容乐观。2013年1月到2019年3月共75个月份，沈阳空气质量月均指数（AQI）Ⅰ级（优）月数0个（0%），Ⅱ级（良）月数47个（62.7%），Ⅲ级（轻度污染）月数22个（29.3%），Ⅳ（中度污染）月数4个（5.3%），Ⅴ（重度污染）月数2个（2.7%）。大气污染已经成为沈阳市迫在眉睫的问题。研究大气污染浓度的变化，掌握其变化规律对大气污染的治理、改善大气污染是十分有必要的。

针对大气污染物浓度预测问题，国内外学者提出了一系列的预测模型。腾浩宇［1］使用多元回归模型预测PM2.5浓度，赵学敏［2］使用灰色GM（1，1）预测模型对北京市大气污染浓度进行预测，但都没有考虑大气污染物浓度数据具有时序性和非线性的特点；岳鹏程［3］使用模糊时序和支持向量机对SO2浓度进行预测，解决了大气污染物时序性特点，但支持向量机中的参数难以确定，参数的选取过于依赖主观经验［4］；范竣翔［5］建立RNN空气污染时空预报模型，RNN模型擅长处理连续的时间序列数据，但在运算过程中容易出现梯度消失问题。大气污染物浓度数据采集过程中，存在数据质量层次不齐、存在异常值和缺失值等数据质量问题［6］。如果不能选择合适的数据预处理方法，可能会对数据的分析结果产生严重偏差，因此数据预处理方法的选取显得尤为重要。

本文利用LSTM模型擅长处理时序的、非线性数据的特点，具有适用性强、防止梯度消失等优点［7］。与不同缺失值处理方法相结合，建立LSTM空气污染预测模型。主要工作包括：通过箱线图法识别出各种污染物浓度数据中的异常值，并采用异常值视为缺失值的处理方法；使用均值替换法、回归插补法以及多重插补法对数据进行数据预处理，比较三种缺失值处理方法的效果；建立LSTM预测模型，分别使用三种预处理后的数据进行训练与检验，比较LSTM模型的精度。

2 数据预处理

2.1 数据来源

本文所使用的沈阳市大气污染物浓度数据，主要来源于国家空气质量自动监测点位的空气质量自动监测数据。所采集的沈阳市大气污染物浓度数据具体为2016年11月1日 至2019年3月31日，共881天5286个大气污染物浓度的日均值数据，主要包括颗粒物PM2.5，颗粒物PM10，二氧化硫（SO2），二氧化氮（NO2），一氧化氮（CO），臭氧（O3）六种污染物。

2.2 数据异常值分析与处理

异常值的存在会对数据的计算分析带来不良影响，本文采用箱线图法分析采集数据中的异常值［8］，箱线图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值［9］，如图1所示。据统计六种污染物异常值共为57个，占总数据的4.15%。同时采用异常值视为缺失值的方法，对异常值进行填补。

图1 六种污染物异常值识别

2.3 数据缺失值识别与处理

数据收集的过程中，由于数据采集失误、数据存储失败、机器损毁等原因会导致数据的不完整性。一般来说，缺失值的处理包括两个步骤：即缺失值数据识别和缺失值处理。

原始数据缺失值的识别如图2所示，按照不同类别和比例，展示了大气污染物浓度原始数据的基本情况，浅色表示浓度值小，深色表示浓度值大，黑色表示缺失值。

图2 原始数据缺失值识别

本文采集的大气污染物浓度数据总量为5286条，缺失量为237，缺失率为5.38%。表1对原始数据缺失值进行了详细统计。本文分别使用均值替换法、回归插补法以及多重插补法［10］，对缺失值进行处理，并比较其处理效果。

表1 缺失值统计

均值替换法保留了与缺失变量无关的其他变量的信息，最大程度上保证了数据真实性与完整性的特点［11］。即采用均值替换法分别计算出PM2.5均值为44、PM10均值为81、SO2均值为28、NO2均值为41、O3均值为53、CO均值为1。对污染物浓度数据进行均值替换法处理的频数分布对比，如图3所示。

图3 均值替补法前后数据频数分布图

通过污染物变量与时间变量建立回归模型，利用回归方程的预测值对缺失数据进行回归插补［12］。对污染物浓度数据进行回归插补法处理的频数分布对比，如图4所示。

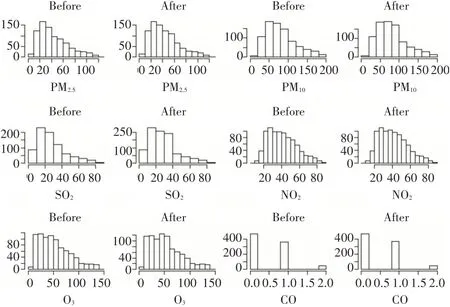
图4 回归插补法前后数据频数分布图

对原始数据进行多重插补，利用每一个插补值对缺失数据插补得到相应个数的完整样本［13］。对污染物浓度数据进行均值替换法处理的频数分布对比，如图5所示。

图5 多重插补法前后数据频数分布图

通过以上三种方法对原始数据时间序列集进行缺失值处理后，可明显看出，处理后数据频数发生了明显变化。沈阳市六种污染物浓度变化的时间序列分布折线图如图6所示，六种污染物浓度变化趋势具有较为明显的周期性特征。其中PM2.5、PM10、SO2、NO2每年的11月份到次年的3月份浓度较高，主要原因是沈阳市仍然以燃煤为主，冬天采暖期煤的消耗量较大，供暖期的燃煤量是非供暖期的3倍［14］，使得冬季这四种污染物浓度较高；每年2月至8月O3的浓度较高，主要原因是夏季沈阳市温度较高，同时汽车保有量的迅速增加［15］也是O3浓度升高的原因之一。CO浓度值主要在（0，2）之间波动，对沈阳市空气质量的影响较小，故本文不进行CO污染物浓度变化研究。

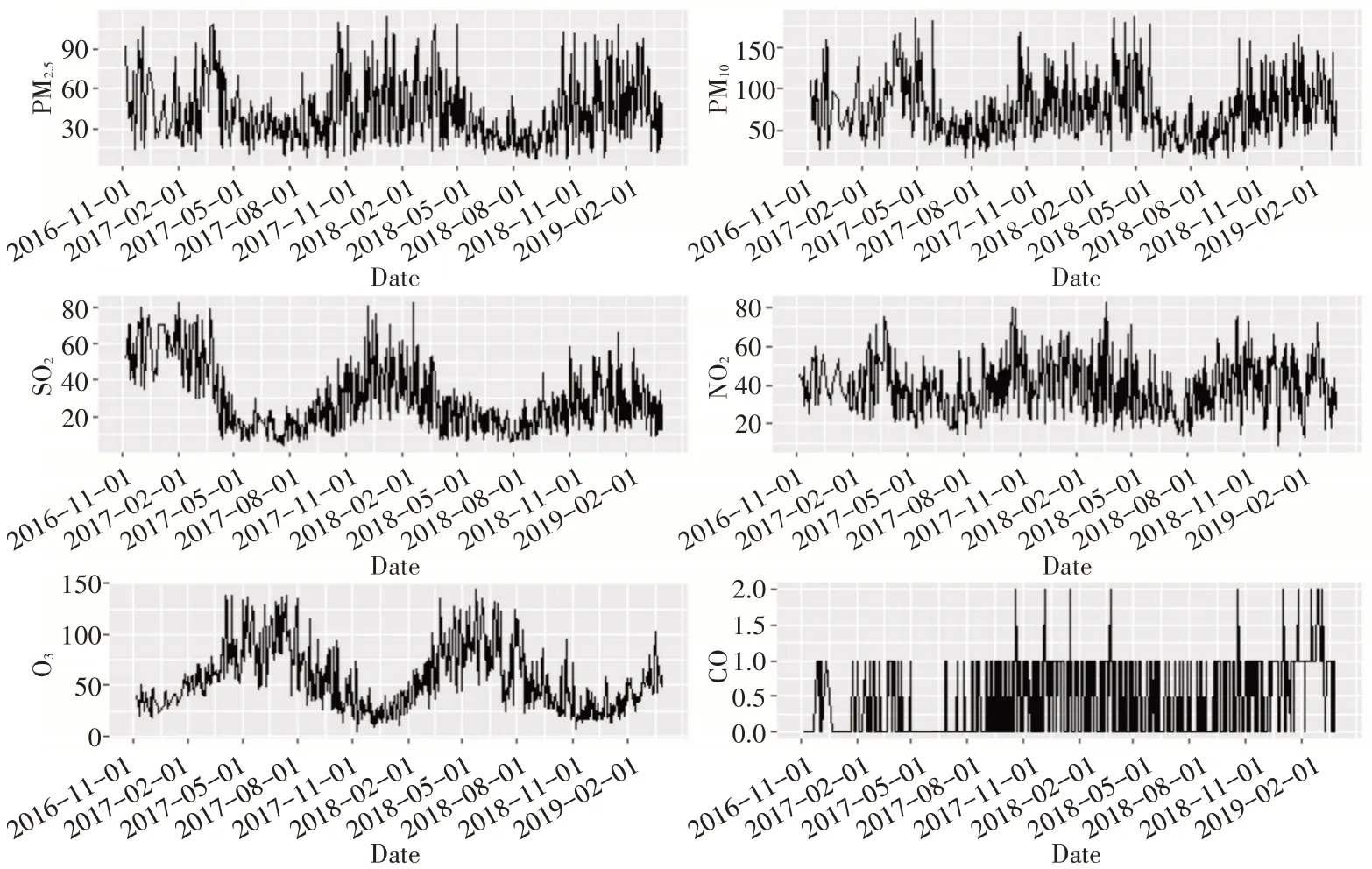
图6 六种污染物浓度时间序列分布折线图

3 模型建模

3.1 LSTM神经网络简介

长短期记忆网络（Long Short-Term Memory Network，LSTM）是循环神经网络（Recurrent Neural Network，RNN）的变形结构［16］，在隐藏层各神经单元中增加单元状态量，使时间序列上的记忆信息可控；在隐藏层各单元传递时通过遗忘门、输入门、输出门控制历史信息与当前信息的记忆和遗忘程度。

3.2 输入层、输出层神经元设置

本文采用三层神经网络结构，输入层和输出层是通过实际情况而设计的，输入层输入数据为PM2.5、PM10、SO2、NO2、O3共五个特征变量，神经元个数为5；输出层预测输入层五个特征变量的浓度变化，神经元个数亦为5。

3.3 隐藏层神经元设置

目前对于隐藏层神经元个数的选取没有准确的算法公式，只能结合经验公式和不断进行试验的方式来确定［17］，经验公式如下：

其中n为输入层的神经元个数，n1为输出层神经元个数，a是（1，10）范围内的任意整数，M是隐藏层的神经元个数。由式（1）可得，M的取值范围是（4，13），式（2）可得M取值为3，故隐含层的神经元个数范围为（3，13）之间的整数，在这范围内采用试凑法，对11种不同隐藏层神经元个数进行对比训练，利用MAE和RMSE作为模型精度评价指标（式（3）和式（4）），找出最合适的隐藏层神经元个数为3。激活函数为Sigmoid，学习率（learningrate）设置为0.01，每次训练输入的样本数（batch_size）为50，迭代次数（numepochs）为150次。

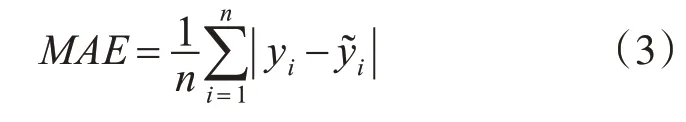
式中：MAE为平方绝对误差，n为数据总个数，yi为数据的真实值，y͂i为数据的预测值。

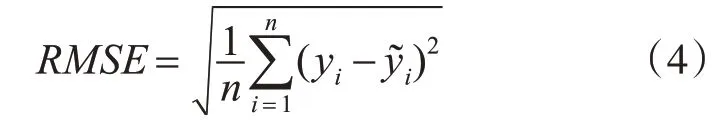
式中：RMSE为均方根误差，n为数据总个数，yi为数据的真实值，y͂i为数据的预测值。

4 实验分析

通过三种不同数据预处理形成三组新的数据集，以及直接删除缺失值的原始数据集，分别对这四组数据集进行归一化处理，并分别选取2016年11月~2018年12月 数 据 作 为 训 练 集，2019年1月~2019年3月数据作为测试集；利用前一天五种污染物浓度值作为模型输入，后一天五种污染物浓度值作为模型输出，进行LSTM模型仿真实验，实验结果如表2、表3所示。

表2 缺失值处理方法的预测精度评价指标MAE对比

表3 缺失值处理方法的预测精度评价指标RMSE对比

通过表2、表3可知，模型的隐藏层神经元个数为3时，模型的评价指标最好，并且不同缺失值的处理方法的评价指标也不同，故对缺失值处理方法与模型精准度进行排序如表4所示。

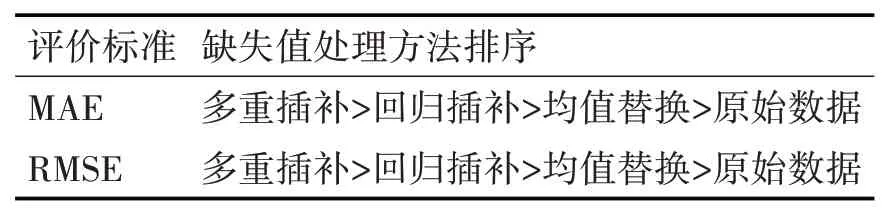
表4 隐藏层神经元个数为3的缺失值处理方法排序

通过以上分析可得：多重插补法的RMSE和MAE的值均为最小，模型的预测精度最高，而原始数据的预测精度最低。与原始数据相比，多重插补法的精准度评价指标MAE提高了22%，RMSE提高了13%，所以应采取多重插补法进行缺失值处理；图7是采用多重插补法的LSTM模型对五种污染物浓度的原始数据与预测结果的曲线对比图，可以看出该模型对污染物浓度的变化趋势预测较好，根据模型计算出MAE误差约为13.3，预测值与实际值拟合较好，同时具有良好的泛化能力。

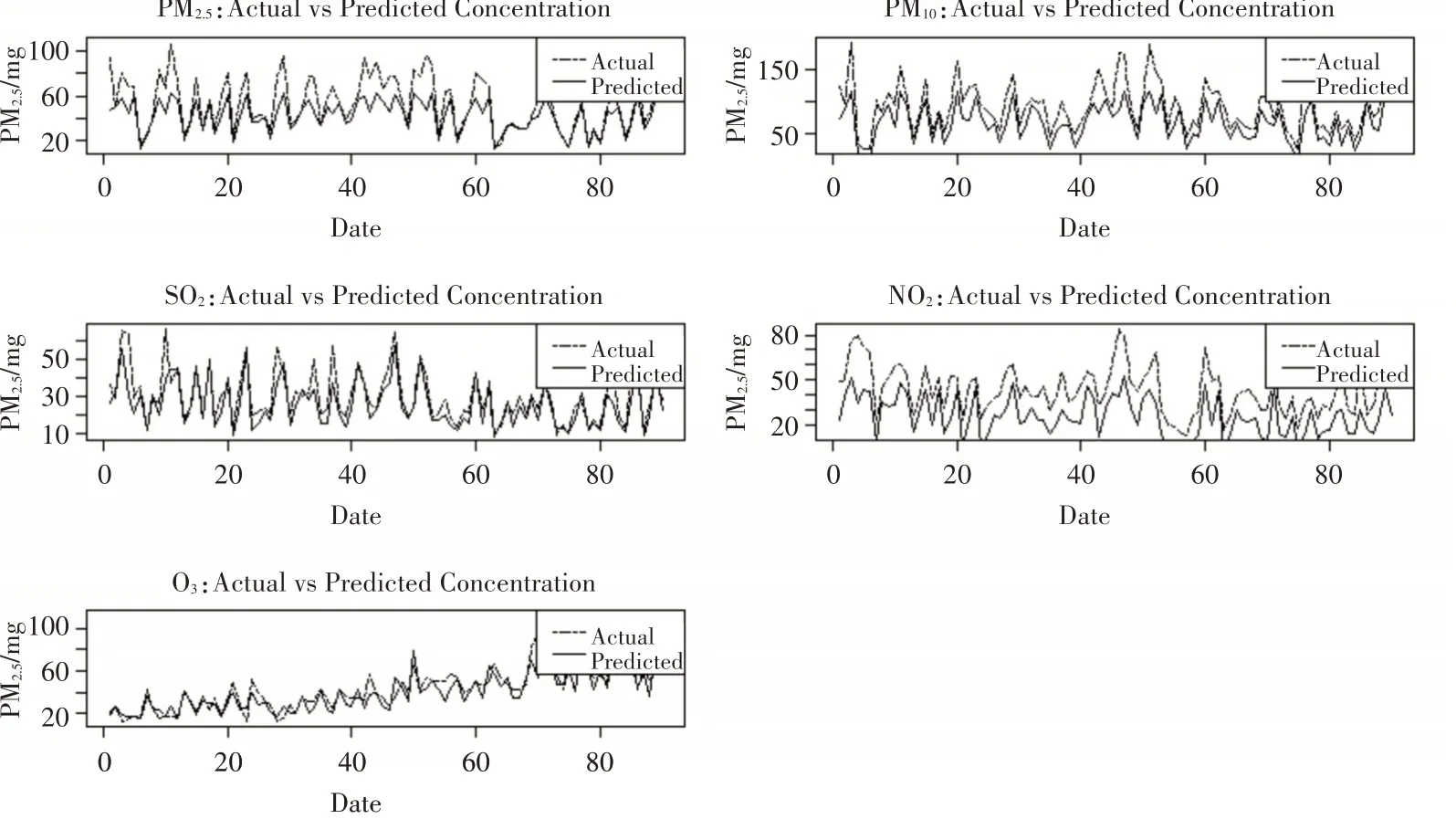
图7 多重插补法的LSTM预测模型对图

5 结语

通过对沈阳市8个国控站点数据的采集、处理和挖掘，得出沈阳的主要污染物是PM25、PM10、SO2、NO2、O3，同时污染物浓度变化具有一定的周期性。本文建立三层LSTM时间序列模型可以精确地预测五种污染物浓度，实验结果表明通过数据和缺失值预处理，可以有效提高预测精度，其中多重插补法的精度提升最高。本文对于LSTM模型的隐藏层神经元个数设置，采用的是经验公式法和试凑法的结合，因此隐藏层神经元的最优个数的选取上仍然有进一步优化的空间。