面向任务的某型两栖装甲装备备件配置优化模型∗
王 宝谭 鹏陈武锦张 峥
(1.海军航空大学 烟台264001)(2.92279部队 烟台264001)(3.92510部队 湛江524000)
(4.91980部队 烟台264001)
1 引言
两栖装甲装备是两栖装甲部队遂行多样化军事任务的主要武器,其备件保障工作质量是直接影响装备战技术性能良好的重要因素,也是保持部队作战能力的一项基本要素。当前,装备备件的配置保障在很大程度上是凭经验进行备件需求量的确定,缺乏科学的配置保障方法。需要对携行备件配置优化问题进行研究,其中包含两项内容:一是为了在有限的经费条件下,尽量提高装甲装备的使用可用度;二是为了在保障率一定的情况下,在满足部队训练的前提下,控制购买备件的费用,使经费最小化[1~5]。
2 携行备件配置优化模型
本文进行配置优化考量的两个主要指标是总经费和系统保障率,在备件初始使用情况相同的前提下,对零件的单价和保障率、部件的可更换新和装机重要性、装备的保障率等因素进行分析。为此,我们分别从经费一定的约束条件下求系统的最大保障率和系统的保障率一定的约束下求出系统的最小经费两个方面考虑建立模型[6]。
2.1 模型一
在经费一定的约束下求系统的最大保障率,其目标函数如式(1)所示:
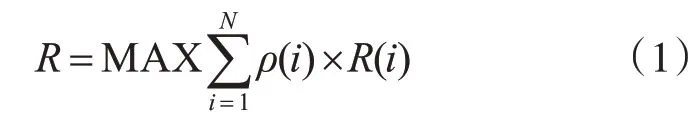
式中:ρ(i)为第i个部件的权重;R(i)为第i个部件的保障率;R表示对各部件的保障率与权重的乘积进行求和,并且确定其最大值。
约束函数:
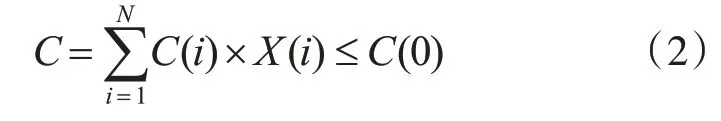
式中:C(i)为第i个部件的单价;X(i)为第i个部件的需求数量,非负整数;C(0)为系统给定的总费用;C表示对各部件的数量和单价的乘积进行求和,并且使其值小于或等于系统总经费C(0)。
R(01)≤R(X(i),T)≤R(02)i=1,2,…,N(3)式中:R(01)为最小保障率;R(02)为最大保障率;R(X(i),T)表示各部件在订货周期内的保障率大于或等于最小保障率R(01),小于或等于最大保障率R(02)。
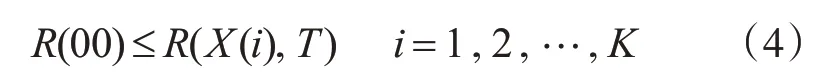
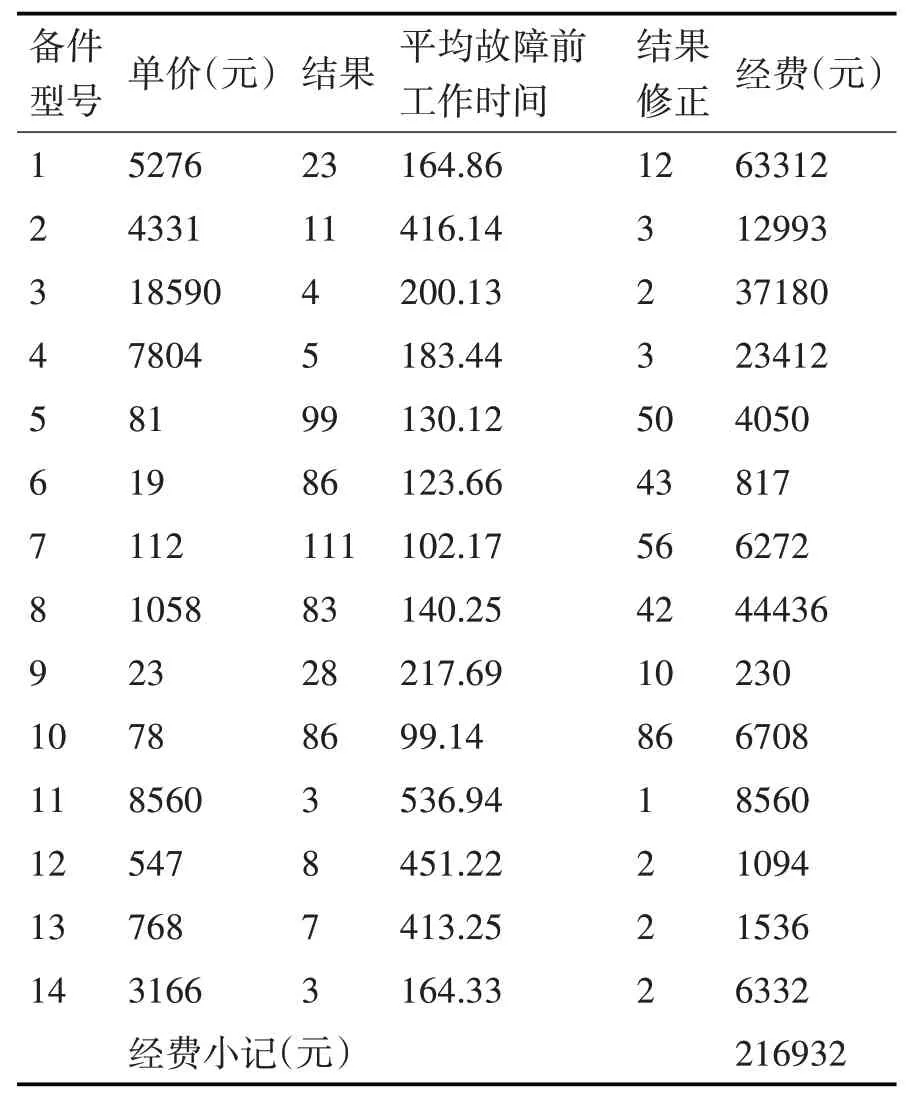
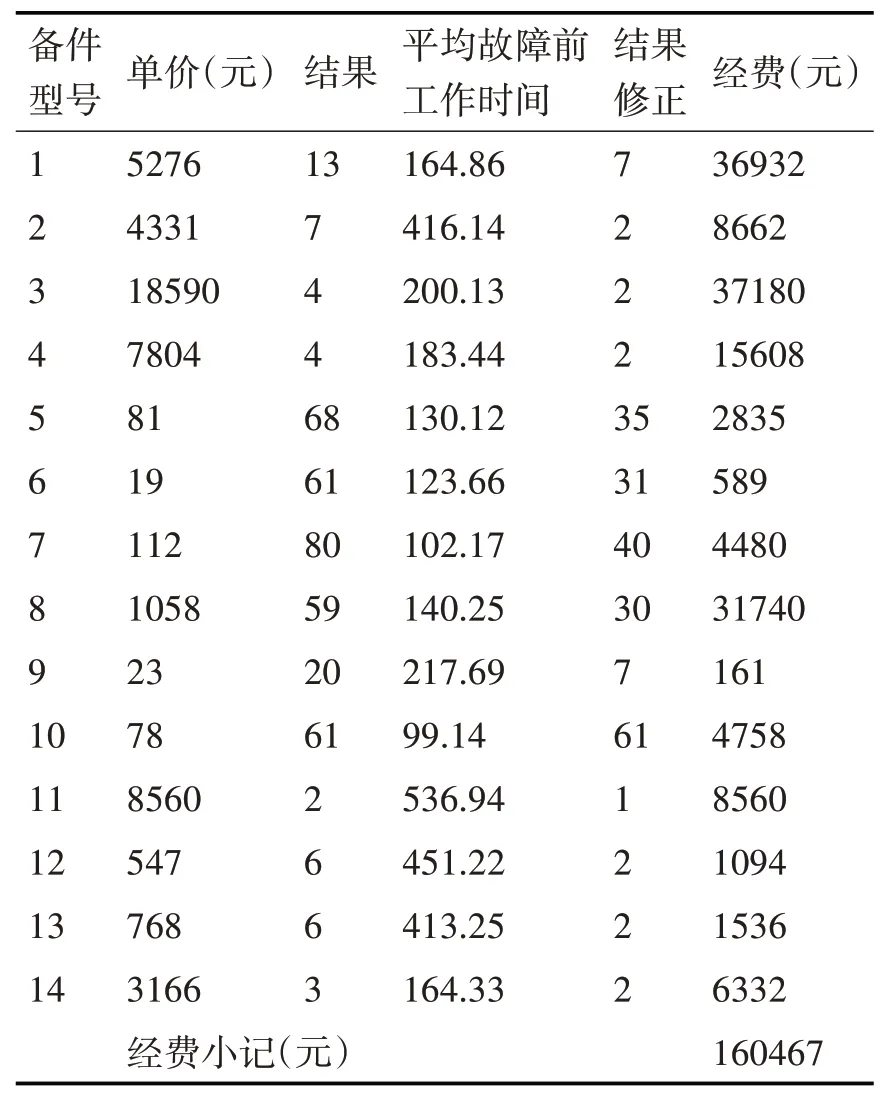
式中:R(00)为拟求得的最大保障率,大于或等于最低保障率R(01),小于或等于最大保障率R(02);R(X(i),T)i=1,2,…,K表示其中若干个特别重要的备件的保障率,大于保障率R(00),K 保障率定义: 式中:λ(i)为第i个部件的故障率;N(i)为第i个部件总的备件需求数量;Tk(i)为第i个部件的第k个需求周期。 在系统的保障率一定的约束下求出系统的最小经费。其目标函数如式(6)所示: 式中:C(i)为第i个部件的单价;X(i)为第i个部件的需求数量,非负整数;C为对各备件的单价与数量的乘积进行求和,并且使其最小化。 约束函数: 式中:R(01)为最小保障率;R(02)为最大保障率;R(X(i),T)表示各部件在订货周期内的保障率大于或等于最小保障率R(01),小于或等于最大保障率R(02)。 式中:ρ(i)为第i个部件的权重;R(i)为第i个部件的保障率;R(0)为材料给定的总保障率。 表示当第J个备件缺件一个时,系统总保障率R小于R(0)。也就是说只有备件不缺件时,系统总保障率才能达到R(0)。 权重表示部件在装备系统中作用的大小。权重大表示该部件的故障率、备件可更换性或对装备的重要性较大,反之亦然。本文对每个备件从故障率、可更换性和的重要性三个方面进行权重值分配。假设每个备件的权重分配满分是n,其中故障率为0.7n,部件的可更换性为0.1n,重要性为0.2n。根据每一个部件的故障率的大小、可更换性和重要性的大小给该部件赋予相应的值。再对该部件的分数求和,确定该部件的权重的分数,然后与总权重的分数相除确定该部件的权重[7~9]。 2.3.1 故障率在权重中的分析D 按故障率的大小可以将故障分为灾难故障、致命故障、临界故障和轻度故障,灾难故障和致命故障等故障率高的部件在权重7分中占有分数比临界故障和轻度故障等故障率低的部件大。当然这样做有很大的随机因素和相当大的不确定性,也可能对最后的权重结果有很大的影响,但是作为一种分析权重方法是可行的[10]。 2.3.2 可更换性在权重中的分析E 可更换性是指备件拆装的难易程度,这里把备件分为易更换件与难更换件。单纯依靠人力即可完成拆装的备件称为易更换件;需要借助装甲抢修车等机械装备,才能完成备件拆装的备件称为难更换件。考虑到备件性质不同,特别是难更换件一般不更换只随着装备退役,将易更换件的权重值分配为1分,将难更换件权重值分配为0分。 2.3.3重要性在权重中的分析F 每一个部件在两栖装甲装备上的重要性是不同的,若某部件是装备上的关键部件,一旦出现故障,会严重影响装备的战技术性能,甚至使装备性能完全丧失,应当分配更大的权重值。 按照上述步骤对每一个部件进行三项权重值的分配,进行后求和得到该部件的权重分数ri,然后在对所有部件的权重分数ri进行求和,得出一个总权重分数则部件的权重为ρi=ri/R。 优化问题的最一般形式数学描述如下: 约束因素和优化变量的数目以及目标函数和约束条件的性质是影响影响最优问题求解效率的关键因素[13~14]。约束优化问题根据约束条件的性质可分为:线性约束优化问题和非线性约束问题。其标准形式分别如下所示。 线性约束问题: 非线性约束问题: 求解约束优化问题主要有两个思路:直接对目标函数采用搜索法和对目标函数进行转换化为更易求解的问题[15~16]。 在模型一中,目标函数是求在系统经费C一定的前提下系统的最大保障率的值作为系数矩阵f;在约束条件R(01)≤R(X(i),T)≤R(02)中,我们将其设置为优化问题中上下边界约束条件lb和ub;在经费约束条件中,我们将备件单价C(i)及总经费C(0)作为命令中的不等式A、b,而将等式约束的Aeq、beq分别设为空值,初始变量x0的值取为0,算法采用标准算法。利用计算的结果,并进行修正。 在模型二中,目标函数是在装备总保障率一定的情况下求解计算系统的最小经费C,其中我们将备件单价C(i)作为优化问题中的系数矩阵f,而将约束条件中的系统总保障率的约束条件作为不等式约束A、b,取备件的最小与最大单件部件保障率的取值范围R(01)≤R(X(i),T)≤R(02)作为优化问题中配置变量x的上下边界即约束条件lb和ub,R(0)作为对满足备件总保障率的备件数量的限制,将其作为对不等式约束的补充,而将等式约束的Aeq、beq分别设为空值,初始变量x0的值取为0,算法采用标准算法。利用计算的结果,并进行修正。 为检验部队两栖登岛作战能力,组织部队赴某地进行实兵对抗训练。红军为1个两栖机械化步兵合成营,担负两栖登岛作战任务;蓝军为1个轻型机械化步兵连,担负岛礁守卫任务。按照现代作战原则,为形成对敌优势,红蓝整体兵力对比为4:1;红军装备有两栖装甲装备34台。本次训练的地、海域,常年高温,多雨;训练周期内,受西南季风影响,海浪较大。岛礁地势较平,浅水区域为砂石地质,多珊瑚,地势较缓。 整体特点适合两栖装甲部队进行两栖登陆作战,但对两栖装甲装备的行动系统、操纵系统、电气系统和通信系统影响较大。红军合成营结合作战任务和两栖装甲装备技术性能情况,运用模糊层次分析法,可得,此次训练须携带行动部分备件共计14种[17~20]。 按照年度训练经费使用保障计划,本次对抗红军分队装备行动部分保障经费为40万元。主攻方向装备有两栖装甲车19台;助攻分队装备有两栖装甲车15台。 通过故障数据统计分析,备件9的故障率40.423×10-4,故障率是最大的,将备件9在权重中的分数设为7分;备件13的故障率仅为0.561×10-4,故障率是最小的,其权重值分配为2.5分。通过相同的方法计算分配这些部件的权重值,区间为2.5分~7分。经过历史数据采集和一系列的计算,可得行动部分各部件的权重,具体见表1。 表1 行动部分备件权重列表 为满足Matlab编程中linprog命令语句的格式要求,需要对模型中约束条件与目标函数变量数据进行简化处理。根据两栖装甲装备使用情况,使用的数据是1000h内的故障统计时间,单台装备一个训练周期的运行时间为100h。依据1000h建立的故障分布函数来确定任务备件需求量,需要对结果进行修正。每个部件的平均故障前时间与100h比较,所得数据为该备件的修正系数。例如:备件1的平均故障前时间是164.86h,是100h的1.65倍,取整后得到结果为2;经过优化模型计算的备件数目为23,运算后的结果为11.5;取整、修正后的计算结果为12,即优化后的备件数目取12个。 主攻分队保障率取100%,参与训练的两栖装甲装备数量为19台,运用模型二,经过计算可得备件修正结果和使用经费,具体见表2。 表2 主攻分队备件配置方案 助攻分队保障率取90%,两栖装甲装备数量为15台,经过计算可得备件修正结果和使用经费,具体见表3。 表3 助攻分队备件配置方案 综上分析计算,可得在保障率一定的条件下,红军行动部分备件所需总经费为37.7399万元,小于给定总经费40万元。 在满足主攻方向备件100%保障的前提下,剩余给定经费为18.3068万元,用以提高助攻方向备件的保障率。运用模型一计算可得助攻分队行动部分备件保障数量及保障率。具体见表4。 表4 助攻分队备件配置方案二 通过上述分析计算,可得在保障经费一定的条件下,红军助攻分队行动部分备件的保障率为94.8%>90%。 本文结合携行备件配置优化的需求分析,分别从经费一定的约束条件下求系统的最大保障率和系统的保障率一定的约束下求出系统的最小经费两个方面考虑建立模型。以某两栖装甲部队濒海训练红蓝对抗演习任务为例,进行对比分析,验证了模型的有效性。
2.2 模型二
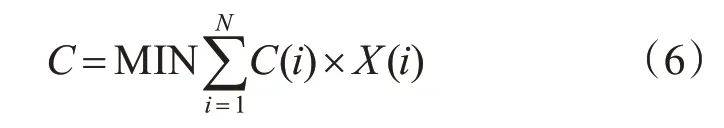



2.3 权重的设定
2.4 权重的求解
3 携行备件配置优化模型求解
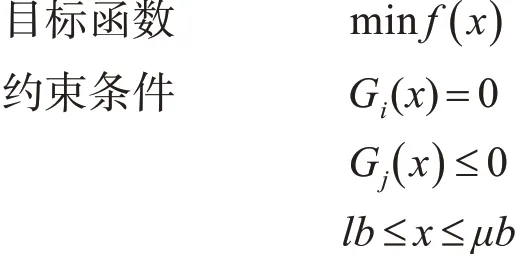
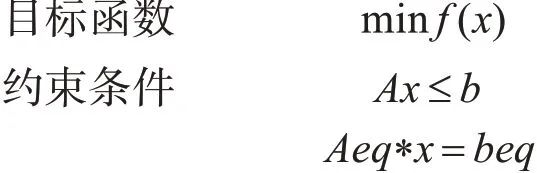

3.1 模型一求解
3.2 模型二求解
4 案例分析
4.1 配置优化模型的建立与求解

4.2 最小经费计算
4.3 最大保障率计算

5 结语

