离港航班延误的动态预测研究∗

王语桐朱金福刘 畅

（1.南京航空航天大学民航学院 南京211106）（2.广西师范大学数学与统计学院 桂林541006）

1 引言

近年来航空运输业发展迅速，航班延误现象频频出现，成为机场和航空公司运营管理的一大难题。通过建立合理有效的延误预测模型，预测未来时刻延误航班数及延误程度，以及时调整运行策略，对于机场和航空公司具有重要意义。

目前，国内外已有相关学者对航班延误预测进行了研究。刘玉洁［1］基于集成学习理论和改进型的贝叶斯网络，建立了一种带有自反馈的集成学习系统，对航班延误进行预测。陈海燕［2］利用动态数据驱动方法进行航班延误预测，并采用支持向量机和滤波方法分别对状态空间模型的关键参数进行回归求解和动态数据的同化。李俊生、赵键涛和HELLWIG M D［3~5］利用贝叶斯网络对航班延误进行预测。罗赟骞等［6］得出进港延误时间序列存在混沌特性，对其进行相空间重构，并证明差分进化算法可获得最优的支持向量回归预测模型。Sina Khanmohammadi［7］引入一种新型神经网络模型来预测航班延误。刘小飞、程华和Yi Ding等［8~10］分别采用融合先验知识的支持向量回归方法、决策树方法与多元线性回归方法建立进港航班延误预测模型。

上述预测方法大多是对航班延误预测为非动态预测，预测结果不具有实时性。而时间序列预测方法会根据航班延误实时变化趋势对航班延误进行预测。因此，提出一种航班动态预测方法，该预测方法基于时间序列，并采用ARMA模型对航班延误进行预测，结合航班延误影响因素，通过支持向量机模型对预测结果进行修正，进而提高模型的预测精度。

2 航班延误动态预测方法

由于航班延误问题较为复杂，航班延误时间序列也具有随机性。本文中利用小波分解方法，基于小波分解多分辨率的特点对航班延误时间序列进行分解，分解尺度为2，这样分解之后可以得到3组数据，将这些数据进行ARMA模型，并对航班延误进行预测。对得到的三组预测结果进行小波重构，得到时间序列的预测结果。最后，将ARMA预测结果与航班延误影响因素输入到训练好的支持向量机，得到最终航班延误预测结果。具体预测过程如图1所示。其中，train为训练集，predict为时间序列预测结果，result为模型的最终预测结果，D1、D2、S2为小波分解得到的三组数据。

图1 航班延误动态预测流程图

2.1 小波分解与重构

对于波动较大的时间序列，利用离散小波分解方法将原始信号分解到不同尺度上，使得非平稳时间序列趋于平稳化。离散小波分解的实质是将原始信号S0从j尺度到j+1尺度的按层分解过程，将前一次分解到的信号再次进行分解，分解之后同样可以得到高频和低频两种信号。具体的分解过程为

其中，Sj，m为第j层的低频信号，m为进行平移操作的参数；Dj，m为第j层的高频信号，m为进行平移操作的参数；h为小波分解时的低通滤波器；g为小波分解时的高通滤波器；k=2m+n，且分别为进行实践伸缩和平移前的低通滤波器和高通滤波器。

经过上式计算后分别通过ARMA模型对未来时刻航班延误进行预测，得到的多组预测结果可以通过小波重构进行重构，重构过程为

以Daubechies小波为基函数，本文中对航班延误时间进行离散小波分解，分解尺度为2，一维2尺度的离散小波分解示意图如图2所示。其中，S0为原始信号，S1、D1分别为尺度为1的两种信号（低频、高频），S2、D2分别为尺度为2的低频、高频信号，且

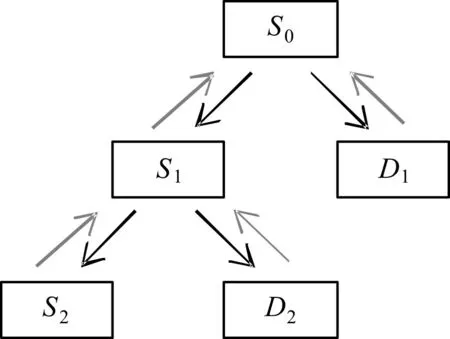
图2 小波分解与重构过程示意图

2.2 ARMA模型建立与预测

ARMA模型是一种常用的随机时间序列预测模型，被广泛应用于时间序列的短期预测。ARMA模型主要是由AR（p）和MA（q）两部分组成，其中心化ARMA（p，q）可表示为

其中，xt为t时刻延误预测值；φp为第p个自回归系数，p为自回归项；xt-p为t时刻之前第p时刻的延误预测值；θq为第q个滑动平均系数，q为移动平均项为白噪声序列。

ARMA模型识别主要在于对自相关系数和偏自相关系数的截尾和拖尾进行分析。表1给出AR（p）模型、MA（q）模型和ARMA（p，q）模型自相关系数和偏自相关系数的性质。

表1 三种模型的自相关系数和偏自相关系数的性质

选用赤池信息量（AIC）准则来判定模型的优良性，将AIC最小的模型视为最优模型，进而确定阶数。再基于最小二乘法对所确定的模型进行检验，分析残差序列是否为特定序列（白噪声），以判定模型的有效性。最后依据模型计算结果选择合适的ARMA模型对航班延误进行预测。

2.3 支持向量机模型建立与预测

支持向量机的基本思想是通过一个非线性映射φ将航班数据zi映射到高维特征空间，并在此空间进行线性回归，十分适合对机场航班延误数据进行回归分析。支持向量机模型可以表示为

其中，n为样本量；zi为输入向量；yi为对应的预测指标数据惩罚系数；C>0，用来平衡回归函数f的平坦程度和偏差大于样本点的个数为松弛因子；ε为足够小的正数；引入拉格朗日乘子得到，其中为核函数，文中选用Gauss径向基核函数（RBF）为核函数，见式（6）。

其中，核参数σ和惩罚系数C是通过网格搜索法和交叉检验法［11~12］确定，即首先在σ和C取值区间内划分若干网格并遍历取值，而后采用10折交叉验证法，选取所有取值中使得均方误差平均值最小的一组为最优参数对。

3 案例分析

为验证模型有效性，选取上海浦东国际机场2019年2月1日至2019年4月9日10：00航班数据作为模型的训练集，预测未来8h内单位小时离港航班延误架次和平均延误时长。

3.1 延误影响因素的确定

根据美国联邦航空局中航空系统性能指标数据库中的机场分析模块，与机场航班起降有关的数据字段主要有以小时为单位的机场进离港架次、进离港延误架次、平均延误时长和航班性质等。通过对已有数据字段进行补充和修改，得到离港航班延误影响因素如表2所示。由于各变量量纲不一致，很可能对研究结果造成影响，故采用最大最小归一化方法对航班数据集进行归一化处理，使得各变量的数据范围缩放到［0，1］之间，其表达式为

表2 变量符号及含义

其中，X和Y分别为归一化前后的数值，Xmax和Xmin分别为样本的最大值和最小值。

3.2 机场能见度

机场能见度作为影响航班延误的主要因素，会严重影响到机场航班的起降。但通过现有天气网站无法获取各地区能见度历史数据，有学者曾得出能见度与大气颗粒物浓度呈现出幂函数关系［13~15］。因此，利用现有2015-2016年浦东机场能见度数据，以及从天气网站下载的历史大气颗粒物质量浓度数据，采用幂函数对机场能见度和颗粒物质量浓度的关系式进行拟合，拟合结果如图3所示。同时得出机场能见度与PM2.5浓度的关系式为：VSB=-292.66PM2.50.64453+11196。由t检 验 和F检验的p值均小于0.05可得，该模型和参数均显著。

图3 机场能见度与PM2.5浓度的关系

3.3 动态预测模型建立

利用尺度为2的离散小波分解对单位小时内离港航班延误架次和平均延误时长时间序列进行小波变换，对分解得到的3组时间序列进行相关系数（自相关、偏自相关）检验，检验结果均显示为平稳时间序列。结合自相关系数和偏自相关系数的截尾和拖尾情况，确定时间序列模型为ARMA（1，1），并根据AIC信息量准则选择最优模型。基于R语言对3组时间序列进行预测［16］，并将预测结果进行小波重构。最后采用支持向量机模型对结果进行修正，模型预测结果和相对误差如表3所示。

表3 模型预测结果

采用均方根误差对模型进行评估，得出单位小时内离港航班延误架次和平均延误时长预测模型的均方根误差分别为8.92%、9.97%。为检验该动态预测模型的实时预测性，选用11：00~14：00航班数据对ARMA模型参数进行更新，同样采用支持向量机模型对未来4h内航班延误预测修正，模型预测结果和相对误差如表4所示。计算模型的均方根误差分别为5.58%、6.86%，较模型更新前降低大约3%。

表4 模型更新后的预测结果

4 结语

提出一种基于时间序列的航班延误动态预测方法，该方法会随新航班数据的产生实时更新AR⁃MA，根据航班延误情况预测后续时刻航班延误情况，来对航班延误进行动态预测，并采用支持向量机模型对ARMA预测结果进行修正。结果表明，随新航班数据产生该动态预测模型的均方根误差降低大约3%。

该研究成果在一定程度上可用于机场运行控制人员监控机场拥挤程度，预测未来时刻航班延误情况，为采取适当的资源调度方案等提供参考，以帮助机场及时发布延误预警信息，调整机场运行调度策略和减少航班延误的发生。