基于YOLOv4的指针式仪表自动检测和读数方法研究*
李 俊,袁 亮,冉 腾
(新疆大学 机械工程学院,新疆 乌鲁木齐 830046)
0 引 言
在有电磁干扰的环境下,数显式、电子式仪表容易发生故障,而指针式仪表却在抗干扰能力、结构和成本方面都有显著的优势,因而被广泛应用于社会的诸多领域。
但是指针式仪表在传统的人工判读过程中,会因注意力不集中、视觉疲劳等原因造成误读。此外,在工况恶劣、安全风险高的场所(强辐射、高温、化工场所等),并不适合人工观测读取仪表数据。因此,进行指针式仪表的自动检测和读数研究具有重要意义。
随着计算机视觉和目标检测技术的不断发展,指针式仪表数据的自动读取技术变得日臻成熟。针对复杂环境中仪表自动检测和读数困难的问题,已有学者做了许多具有指导意义的研究。圆形指针式仪表通常采用Hough圆检测检测进行表盘定位与提取,但该方法易受到外形类似仪表的物体干扰。房桦等[1]利用SIFT(scale invariant feature transform)算法识别仪表,利用快速霍夫变换提取了指针角度。杨志娟等[2]提出了利用ORB(oriented FAST and rotated BRIEF)算法,求解仪表模板图像与待测图像的透视变换矩阵,定位表盘区域,并根据表盘灰度特征信息,提出了基于圆周区域的累积直方图法对指针进行了定位。GAO J L等[3]提出了利用改进的ORB算法实现了仪表的搜索与识别,利用相似特征三角形方法确定了指针回转中心坐标,引导PTZ调整了其姿态。胡彬等[4]通过提取待识别图片和模板图片的KAZE[5]特征,并采用KNN(k-nearest neighbor)算法进行了关键点匹配,进行了特征匹配,从而得到了表盘区域,最后采用概率霍夫变换拟合出了指针直线。
基于特征匹配的方法都需要人工预先标定仪表模板,需要待识别图像和模板之间要具有高度的相似性,检测仪表速度较慢,在一定程度上限制了其应用范围。
笔者提出一种复杂背景下的指针式仪表自动检测和读数方法,通过基于卷积神经网络的目标检测解决上述方法存在的问题;首先利用YOLOv4[6]检测截取仪表区域,消除外形类似仪表的物体和背景环境的干扰,提高指针仪表区域的显著性,然后利用霍夫变换提取表盘,RANSAC直线拟合方法提取指针中心线,结合中心线斜率求出仪表读数,最后通过实际测试验证方法的有效性和快速性。
1 基于YOLOv4的目标检测
用传统方法获取指针仪表图像区域时,需要构建模板图像,选取模板图像必须要满足许多条件,并且模板图像构建较为耗时。而利用YOLOv4进行目标检测,数据收集和模型训练简单,能够快速鲁棒地从相机采集到的图像中检测出仪表。
1.1 YOLOv4模型
近年来,研究人员在目标检测领域取得了很多突破。YOLOv4能够非常好地平衡目标检测的精度与速度。YOLOv4目标检测器结构由输入、骨架网络、颈部、头部4个模块组成。输入端对数据进行了Mosaic增强,骨架网络采用CSPDarknet53,它是在YOLOv3[7]的骨架网络Darknet53的基础上借鉴CSPnet[8]而来,用于提取图像的浅层特征;其颈部采用SPP[9]、FPN[10]、PAN[11]等模块对浅层特征进行了增强,使模型能够学习得到期望的特征;头部采用YOLOv3返回目标的分类和边界框。
1.2 模型的训练和测试
YOLOv4原有模型并未对指针式仪表进行大量的数据训练,在实际检测中无法获得理想的检测结果。因此,笔者针对指针式仪表,在不同背景、光照、拍摄角度、尺度的条件下采集图像,建立VOC格式数据集,训练一个目标检测网络模型;并根据计算机硬件配置和训练需求配置环境,修改YOLOv4网络配置文件参数设置,完成模型训练。
其参数设置如表1所示。

表1 参数设置
笔者采集仪表图像进行训练,模型训练batch数为4 000次,训练总时长为53 h。初始损失值高达2 000;训练过程中损失值迅速下降,batch值达到200后损失值降至5以下,训练结束时模型平均损失值为0.113。
模型的平均损失值曲线如图1所示。
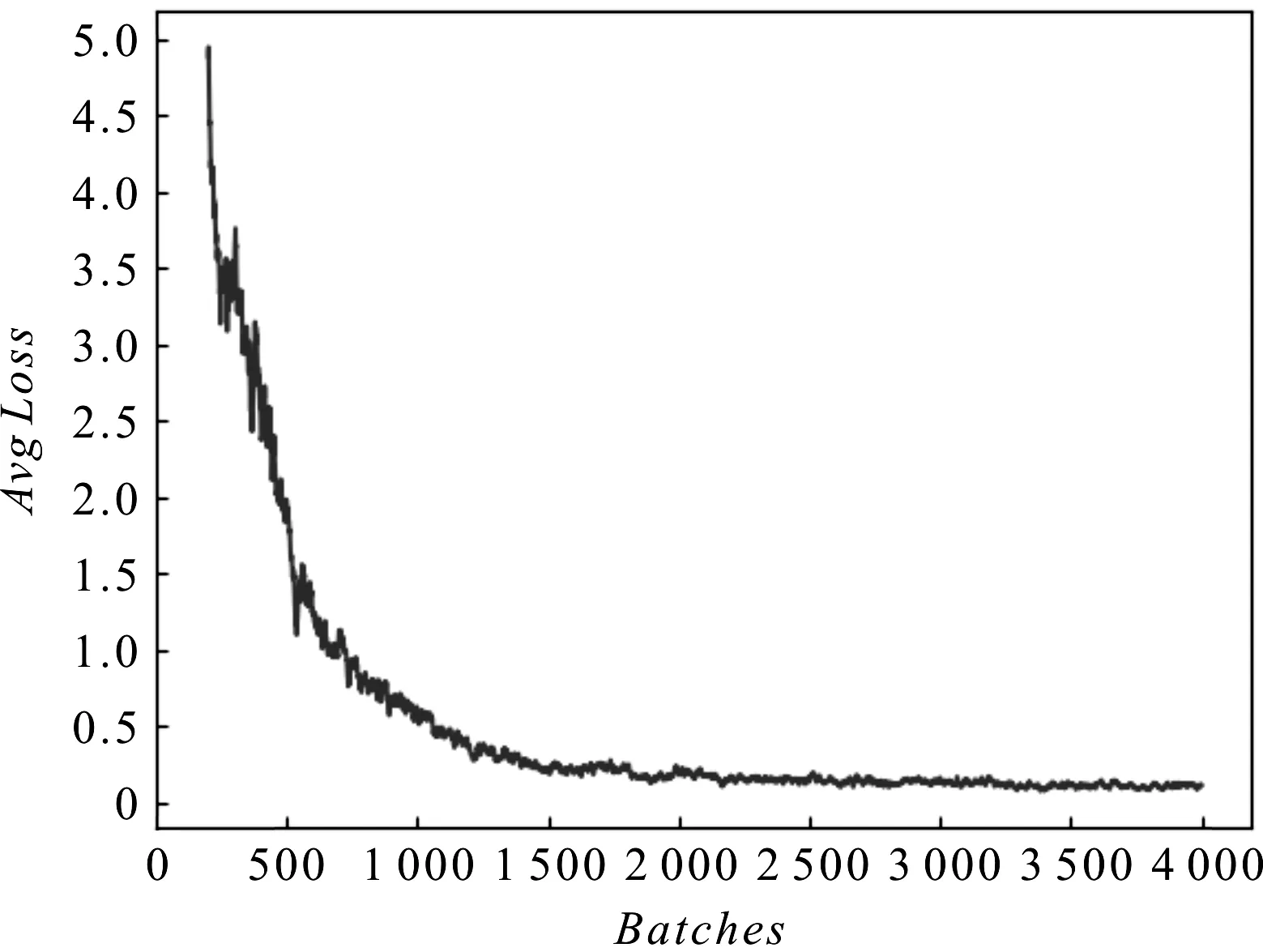
图1 平均损失值曲线
平均交并比如图2所示。
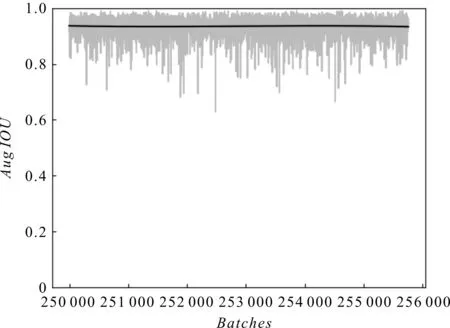
图2 平均交并比变化
模型训练迭代总次数超过2.5×105后,交并比平均值约为0.95;模型的均值平均精度(mAP)达到95.45%。综合各项数据表明,该模型具备较高的目标检测精度。
1.3 仪表检测和提取
传统的仪表检测方法有霍夫圆检测和特征点匹配等。笔者利用霍夫圆检测进行仪表盘检测提取时,当参数调整不合适,或存在与仪表外形类似的圆形物体干扰时,就会导致检测失效。在建立高质量模板的前提下,利用基于特征点匹配的方式检测仪表,检测准确率和检测时间都有较大差异。
传统仪表检测如图3所示。

图3 传统仪表检测
上述方法虽能从背景环境中检测提取出仪表,但大多依赖于高质量的仪表模板,应对环境变化的鲁棒性稍差。
经过数据训练,YOLOv4模型能很好地克服上述方法的缺点。笔者将采集到的图像输入到训练好的目标检测模型,模型会自动返回预测的仪表分类和边界框;在不同条件(不同光照、拍摄角度等)下进行YOLOv4仪表检测实验。
YOLOv4仪表检测结果如图4所示。

图4 YOLOv4仪表检测结果
1.4 表盘区域提取
根据返回的仪表边界框位置坐标可以将绝大部分背景剔除,但仪表指针检测多基于精确的表盘轮廓,所以笔者利用霍夫变换进一步消除残余背景,提取出表盘。
表盘提取结果如图5所示。

图5 表盘提取结果
图5(a)表示图4第一行第二列图,根据边界框剔除背景后的仪表区域;图5(b)表示仪表区域图像经均值滤波、灰度化后,笔者采用霍夫圆变换[12]进行表盘轮廓检测,根据霍夫圆的半径创建mask提取得到的表盘区域。
标准霍夫圆变换将每个非零像素点都视为潜在的圆上点。笛卡尔坐标系下,将经过二维图像上非零像素点(x0,y0)的所有圆映射到abr组成的三维坐标系中,将会是一条三维曲线。遍历图像中每个非零像素点,将得到三维曲线簇。如果abr坐标系中相交于某一点曲线数量,超过给定阈值则点(a,b,r)在二维图像上是圆。但这样计算量特别大,运算速度慢。
笔者采用霍夫梯度圆检测方法,先筛选候选像素点,即先求图像梯度,将梯度值大的区域视为潜在的圆的边缘,只对这些区域进行检测,大幅降低了计算量。
笛卡尔坐标系下圆方程为:
(x-a)2+(y-b)2=r2
(1)
其简化方程为:
a=x-rcosθ
b=y-rsinθ
(2)
式中:(a,b)—圆心;r—半径;θ—半径与x轴之间的夹角。
2 刻度线轮廓直线拟合
由于光照等原因,表盘轮廓边缘可能会导致利用霍夫变换得到的指针回转中心不准确。表盘中多数刻度线轮廓往往较为清晰,根据刻度线都指向指针回转中心的特点,笔者利用最小二乘法[13-15]拟合刻度线轮廓直线,拟合直线交点的平均值点即为指针的回转中心。
刻度线轮廓直线拟合分为刻度线轮廓查找和最小二乘刻度线直线拟合两个步骤。
2.1 刻度线轮廓查找
真实环境下光照条件多变,采集到的图像可能出现光照不均匀的情况。笔者利用自适应阈值分割进行了图像二值化,然后执行膨胀与腐蚀操作;对二值图像进行了连通组件分析,得到了连通组件的轮廓点集;轮廓点集中包含无效轮廓,笔者利用刻度线都集中在表盘圆附近和刻度轮廓有特定横纵比的特点,对轮廓进行了筛选,进而得到了刻度线轮廓。
刻度线轮廓如图6所示。

图6 刻度线轮廓
2.2 最小二乘刻度线直线拟合
最小二乘直线拟合是通过最小化偏差平方和来寻找刻度线轮廓点集的最佳函数匹配。其直线的截距式公式为:
y=ax+b
(3)
式中:a—直线斜率;b—y轴上的截距。
平方偏差求和公式为:
(4)
式中:(xi,yi)—刻度线轮廓外接最小矩形点集中的任意点。
笔者根据最小二乘法拟合直线的原理,求解关于a,b的最小平方偏差和函数的最小值。偏差和的偏导公式分别为:
(5)
(6)
通过求解上式可得到轮廓拟合直线。
刻度线直线拟合和指针回转中心如图7所示。

图7 刻度线直线拟合和指针回转中心
由图7(a)可看到刻度线轮廓直线拟合结果;所有的刻度线拟合直线会相交,交点坐标的平均值点即为指针回转中心;由图7(b)可看到求得的指针回转中心。
3 仪表指针定位
轮廓点集中去除刻度线、表盘边缘及杂点轮廓后,受到表盘中字符干扰,仍无法得到精确的指针轮廓。笔者对指针轮廓进行细化,得到了指针骨架,利用RANSAC[16]算法去除了由字符影响产生的骨架中离群点,进而拟合了指针骨架直线,得到了精确的指针中心线。
笔者对指针轮廓图像进行了Canny边缘检测,用概率霍夫变换直线检测指针边缘直线,得到了指针顶点。
指针定位过程如图8所示。

图8 指针定位过程
4 仪表读数计算
仪表读数计算有角度法和距离法两种方法,其中角度法简单且易于操作。本研究选用角度法计算仪表读数。数字图像以其左上角为原点,水平方向为x轴,垂直方向为y轴。仪表最小刻度线和最大刻度线位置固定,笔者提出以指针的回转中心为原点,建立与图像坐标系相同的仪表直角坐标系。
仪表坐标系如图9所示。

图9 仪表坐标系
计算指针中心直线与水平方向的夹角,换算出指针相对于最小刻度线的回转角度,就能得到仪表读数。
余弦绝对值公式为:
(7)
指针中心线与x轴的反余弦值公式为:
β=arccosK
(8)
式中:(x,y)—指针中心线顶点坐标;(xc,yc)—指针回转中心坐标;K—余弦绝对值;β—指针与x轴的夹角。
根据下面的规则,可得出指针相对于最小刻度的回转角度:
(1)当y>yc:
x>xc时,指针在第一象限θ=5π/4+|β|;
x (2)当y x x>xc时,指针在第四象限θ=5π/4-|β|。 通过计算指针回转角度、最大回转角度和仪表量程之间的比值关系,即可求得仪表读数。仪表读数计算公式为: (9) 式中:θi—指针回转角度;valuei—仪表读数;valuemax—仪表量程最大值;valuemin—仪表量程最小值;R—指针最大回转角度(最大刻度与最小刻度间夹角)。 笔者对准确度等级为1.5的温度表进行检测精度、速度与读数精度的实验。基于特征的检测方式,检测精度与速度取决于对模板质量及仪表图像分辨率的高低,实际的检测精度并不理想,精度均低于50%;与传统的方法相比,笔者所提的方法检测精度更高,仪表检测精度达到了98.6%;并且随着训练集的不断扩充,精度会进一步提高。 笔者对分辨率为720×540的包含仪表的图像进行检测,所采用的YOLOv4检测单帧图像时间为80.65 ms,并且分辨率变化对检测时间影响不大;而基于特征匹配的检测方式时间都在240 ms以上,并且随着图像分辨率的增大,检测时间变长。 各检测方法检测速度如表2所示。 表2 各检测方法检测速度 以绝对误差占量程的百分比作为基本误差来衡量识别精度,基本误差越小,识别精度越高。笔者对量程为100 ℃的指针式温度表进行了50组读数识别精度实验,此处仅展示部分读数识别数据。 读数识别结果如表3所示。 表3 读数识别结果 实验结果显示:本研究算法识别出的数据的平均基本误差只有0.72%,具有较高的识别精度;实验数据中较大的误差主要来自较大的图像倾斜,后续将在校正算法方面进行深入研究,以进一步提升识别精度。 影响仪表识别精度的因素还有镜头畸变和图像倾斜等,实验过程中使用相机本身镜头畸变较小,在仪表检测前通过标定板对相机进行了标定,获得了相机的内参和畸变系数,用其对图像进行了畸变矫正,基本上消除了镜头畸变的影响。 针对仪表自动检测读数时,由于仪表特征不明显、复杂背景环境等因素造成的仪表检测提取困难和速度慢的问题,笔者提出了基于YOLOv4的指针式仪表自动检测和读数方法,并在复杂的背景环境、光照、不同尺度等条件下,对算法进行了实验验证,并得出了以下结论: (1)本研究算法消除了背景干扰,能够快速地从背景中检测提取出仪表,仪表检测精度达到了98.6%,平均检测速度为80.65 ms/f; (2)实际读数实验表明,本研究的读数方法可以准确地识别仪表读数,平均基本误差为0.72%。 本研究算法能对全量程范围角度为270°的指针式仪表实现检测与读数识别,后续通过优化读数识别算法提升了算法通用性;该算法在仪表倾斜、拍摄角度变化时能够快速、精确地检测出仪表,但倾斜和拍摄角度会影响读数精度。 下一步笔者将在图像校正算法方面进行研究,以消除图像倾斜和拍摄角度对仪表读数精度的影响。5 实 验

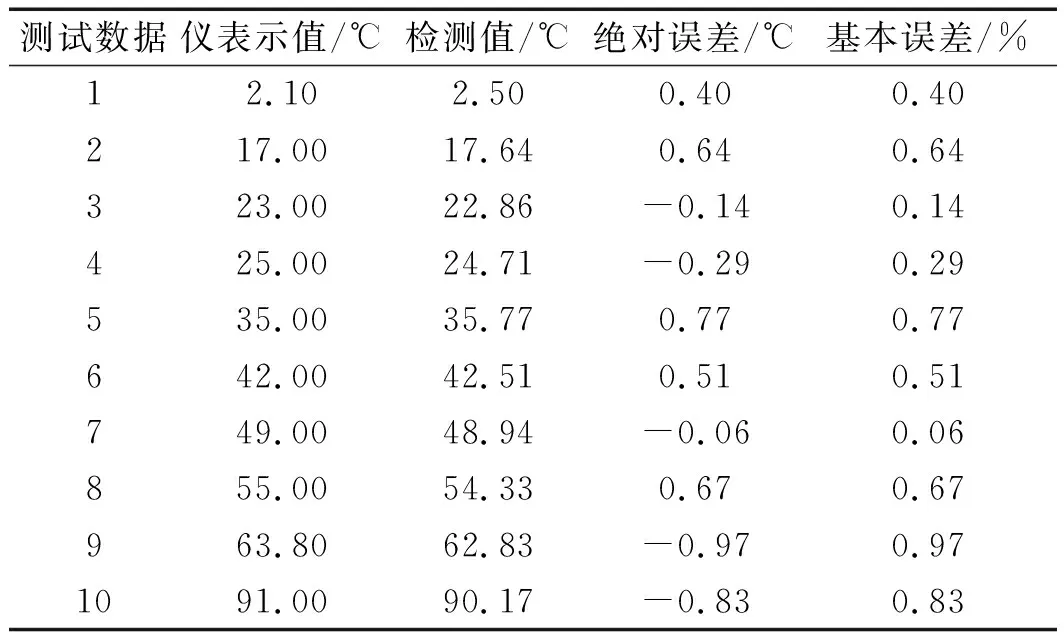
6 结束语

