基于DNGM(1,1)模型的沥青路面技术状况预测分析
赵 永 存
(湘潭市交通建设质量安全监督站,湖南 湘潭 411100)
0 引言
随着中国经济发展,中国公路建设取得了飞速发展,公路养护与管理越来越受到各级部门的重视,交通部在“十二五”公路养护规划中提出,要基本建立国省干道养护科学管理体系。为避免养护资金的浪费,路面养护不及时、路面使用费率上升等不良现象,就需要科学决策,而科学决策的基础就是准确预测路面使用性能。国内外学者对于路面技术状况预测进行了大量的研究,如Gharaibeh将路面性能衰变模型应用于路面养护管理系统,周育名以累计当量轴载为自变量对不同等级公路进行了使用性能预测,张鹏基于MA-MG(1,1)灰色理论预测高速公路路面使用性能等等。
灰色理论目前广泛应用于路面技术状况预测,对于分析因素不确定性、复杂性、多样性,可供参考的历史数据较少,正好可以通过灰色理论优化解决。但在实际应用中,传统灰色理论GM(1,1)在针对路面使用性能预测中存在不少缺陷:如离原始数据序列较近的预测值精度高,但对中长期预测效果欠佳、模型参数估计值存在差分方程到微分方程跳跃性误差等。
以湖南省某地区国省干道为例,基于灰色理论,对传统GM(1,1)模型进行改良,建立基于白化微分方程参数直接估计法的灰色预测模型——DNGM(1,1)模型,对路面技术状况进行评价。
1 沥青路面使用性能预测DNGM(1,1)模型建立
DNGM(1,1)模型主要针对近似非齐次指数序列,为避免模型参数估计值从差分方程到微分方程的跳跃性误差导致模型误差,进一步提高预测精度,从微分方程时间响应函数出发,求解模型参数估计值,进一步通过累减还原得到模型预测表达式。
1.1 DNGM(1,1)模型回归计算过程
设原始数据序列X(0)={x(0)(1),x(0)(2),x(0)(3),x(0)(4),x(0)(5),…,x(n)(t)},其中,x(0)(n)为要预测的某指标在某一时间的原始数据,t=1,2,3,…,n。
利用累加生成(1-AGO)处理,可得:

将新序列的微分方程近似用微分方程表示,满足:
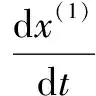
(1)
定义参数a,b,c组成的向量为a=[a,b,c]T,依据最小二乘法性质可得:
a=(BTB)-1BTY;
Y=[x(1)(2),x(1)(3),…,x(1)(n)]T。
解微分方程式(1),得到DNGM(1,1)模型的时间响应函数:
X(1)(t)=(x(1)(1)-b/a+b/a2-c/a)e-a(t-1)+(b/a)×t-b/a2+c/a
(2)
t=2,3,4,…,n
对式(2)做累减还原,得到最终还原式为:
X(0)(t)=(1-ea)(x(0)(1)-b/a+b/a2-c/a)e-a(t-1)+b/at=2,3,4,…,n
(3)
1.2 DNGM(1,1)模型背景值优化方法
DNGM(1,1)模型的求解过程借助传统GM(1,1)模型的求解方法,利用最小二乘法估计模型中a,b,c三个参数的值,求解得到式(2)和式(3)。DNGM(1,1)模型的预测精度取决于a,b,c三个参数,而参数a,b,c的值又取决于原始数据及b的系数值,且背景值z(1)(t)=0.5×(x(1)(t)+x(1)(t-1))的计算方式又给模型参数计算带来一定的误差。分析如下:
对式(1)在区间(t-1,t)上积分,可得:
化简可得:
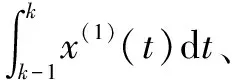
故可得到如下预测模型:
(4)
2 工程实例分析
路面技术状况包含多方面的属性,依据JTG 5210—2018公路技术状况评定标准,路面技术状况应采用路面技术状况指数(PQI)评定,路面技术状况指数(PQI)包含路面损坏状况指数(PCI)、路面行驶质量指数(RQI)、路面车辙深度指数(RDI)、路面跳车指数(PBI)、路面磨耗指数(PWI)、路面抗滑性能指数(SRI)、路面结构强度指数(PSSI)等7个方面。
PQI应按式(5)计算:
PQI=wPCIPCI+wRQIRQI+wRDIRDI+wPBIPBI+wPWIPWI+wSRISRI+wPSSIPSSI
(5)
其中,wPCI为PCI在PQI中的权重;wRQI为RQI在PQI中的权重;wRDI为RDI在PQI中的权重;wPBI为PBI在PQI中的权重;wPWI为PWI在PQI中的权重;wSRI为SRI在PQI中的权重;wPSSI为PSSI在PQI中的权重。
PQI各分项指标权重取值见表1。

表1 PQI各分项指标权重表
其中在计算PQI时,路面抗滑性能指数SRI和路面磨耗指数PWI应二者取一,路面结构强度指数PSSI不参与PQI评定。
以湖南省某地区S331省道二级公路沥青路面为例,共计检测评价里程为14.128 km,双向两车道,设计时速60 km/h,以其中K50~K60为检测路段,2015年—2019年养护数据建立DNGM(1,1)模型(见表2)。
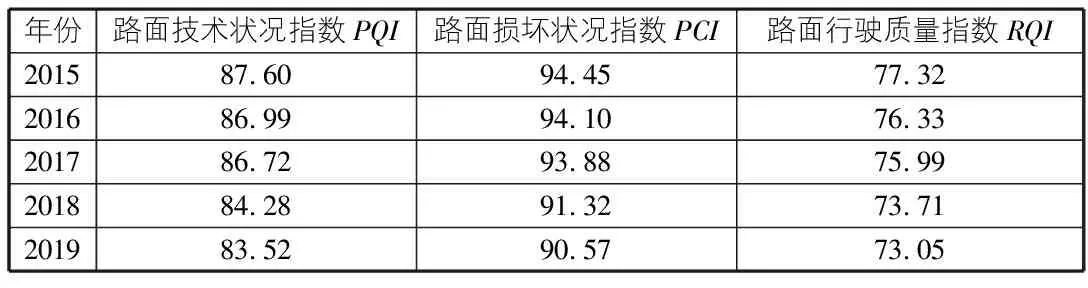
表2 路面技术状况指数DNGM(1,1)模型样本
利用数学分析软件建模分析,分别利用DNGM(1,1)模型与传统GM(1,1)模型对该路段路面损坏状况指数PCI、路面行驶质量指数RQI、路面技术状况指数PQI进行回归分析,并对2020年指标值进行预测。预测结果见表3,预测数据及预测相对误差见图1,图2。
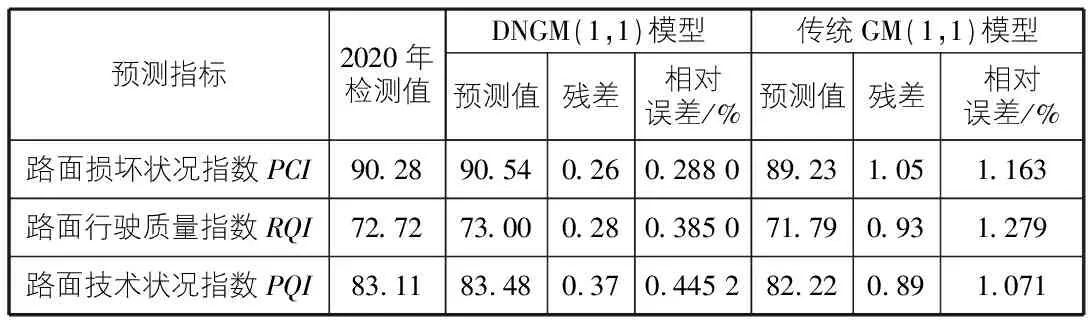
表3 DNGM(1,1)模型与传统GM(1,1)模型预测结果


由表3,图1,图2分析,DNGM(1,1)模型的路面损坏状况指数PCI、路面行驶质量指数RQI、路面技术状况指数PQI预测值与实测值得到的残差均优于传统GM(1,1)模型,说明DNGM(1,1)模型具备较为理想的预测精度,能较为全面的反映数据变化规律,跳跃性弱,稳定性较好,能避免过度拟合和欠拟合的情况发生。
利用DNGM(1,1)模型预测S331省道二级公路沥青路面损坏状况指数PCI、路面行驶质量指数RQI、路面技术状况指数PQI最大相对误差为0.445 2%,最小相对误差为0.288 0%;传统GM(1,1)模型预测的最大相对误差为1.279%,最小相对误差为1.071%,两种预测模型相比较而言,DNGM(1,1)模型预测精度优于传统GM(1,1)模型,具有较高的预测精度,能在小样本范围内,有效解决时间响应问题,具备较高的实用价值。
3 结语
基于灰色理论,对传统GM(1,1)模型进行改良,建立基于白化微分方程参数直接估计法的灰色预测模型——DNGM(1,1)模型,通过对湖南某地区S331省道二级公路沥青路面技术状况进行预测分析,与传统预测模型进行比对,结果表明DNGM(1,1)模型优于传统预测模型,具有较高的精度和稳定性,能准确反映沥青路面的技术状况,可用于公路领域沥青路面技术状况性能预测,为公路养护维修提供参考。

