空间兵棋多因素多步骤裁决模型研究
秦江涛,张 进,郭 帅,罗亚中
(国防科技大学空天科学学院,长沙 410073)
0 引言
西方部队经过大量的实战,验证了兵棋在作战指挥模拟、决策制定和作战伤亡预测等方面都具有很强的应用价值[1-2]。近年来,以各类卫星为主体的空间力量对战争进程和结局产生了巨大影响,传统的兵棋推演已经不能完全满足现代战争推演的需求,必须运用空间兵棋推演的方式来研究空间力量作战问题,来探索发现空间力量运用的特点规律,推动空间力量作战理论创新。这是信息化战争实现科学决策、精确指挥的必然要求,具有十分重要的军事意义[3-4]。
对于我国来说,空间兵棋是一个新兴领域无历史数据和经验数据可用,因此,本文在进行裁决研究时用的是仿真数据,若裁决模型能够反映仿真数据的特性,那么有理由相信裁决模型也能够反映未来真实数据的特性[5]。本文研究的空间兵棋裁决虽然是具体的对抗过程,但研究对象卫星棋子的价值却有战略级的意义,因此,在仿真实验结果的评估上考虑的更加宏观。
1 空间兵棋的特点
兵棋裁决是指通过实时地获取战场信息,量化战场天气、武器性能、态势感知等对不同作战环节产生的影响,依据裁决规则对各环节的作战结果、作战效果进行概率裁决[6]。
对比传统兵棋,空间兵棋在战场天气、武器性能、运动特点等方面有很大的差异。战场天气方面,传统兵棋只考虑大气层内的天气情况如雨雪云等,而空间兵棋还要考虑太空环境如太阳风、电磁干扰等;在武器性能方面,传统兵棋主要以地面设备为棋子,其性能一般简化为攻击力、防御力、机动力等,而空间兵棋主要以卫星为棋子,其在攻防和机动方面受轨道动力学约束,因此,在攻防中不能简单地以攻击力和防御力来描述;在运动特点方面,传统兵棋的棋子只有在接受到命令时才进行机动,运动特点简单直观[7-9]。空间兵棋中,卫星棋子相对地面运动速度极快且轨迹复杂。
综上所述,空间兵棋相对于传统兵棋差异很大,因此,在空间兵棋的裁决模型上要针对其特点进行设计。
2 量化裁决模型——“横向分类型,纵向分步骤”
量化裁决模型是为了求出某类型棋子执行任务过程中各环节影响因素的量化值,以便后续的概率裁决。本节通过对空间兵棋量化裁决的特点分析,提出了“横向分类型,纵向分步骤”的量化裁决模型[10]。
2.1 空间兵棋量化裁决模型分析
传统兵棋是针对棋子机动力、防御力、兵力等因素的简单量化,粗略表达双方棋子在某个属性方面的强弱关系。而空间兵棋因素复杂,如太阳高度角、太阳目标装备夹角等,无法简单量化,必须根据棋子初始状态(轨道六要素和历元时间等)通过量化裁决模型计算各影响因素的量化值,因此,针对空间兵棋的特点需要提出新的量化裁决模型。
在空间兵棋推演中,卫星棋子根据其类型的不同可划分为:侦察卫星棋子、通信卫星棋子、预警卫星棋子等。不同类型的卫星棋子在执行任务过程中涉及到不同的任务环节,而每一个任务环节又包含着不同的影响因素。因此,这实际上是一个“棋子类型-任务环节-影响因素”的3 层链式关系,其关系如图1 所示。

图1 棋子类型-任务环节-影响因素关系图
其中任务环节包括目标感知、目标锁定、任务实施、实施效果等4 个环节,影响因素包括装备因素、态势感知因素、目标因素、天气因素、地形因素和人员因素等6 大类型。
由图1 可知不同类型棋子,在裁决过程中都有目标感知、目标锁定、任务实施、实施效果4 个裁决环节,但不同类型的棋子4 个裁决环节的影响因素是不相同的。例如,侦察卫星棋子的目标感知环节包含的影响因素,和气象卫星棋子的目标感知环节包含的影响因素是不完全相同的。因此,如果按“棋子类型-任务环节-影响因素”3 层链式关系设计裁决模型,就要针对每种类型的棋子设计一种裁决模型,因空间兵棋棋子类型复杂多样,这将会是一个很大的工作量。且当后续有新的棋子类型加入时,裁决模型也不便于扩充。因此,本文提出了“横向分类型,纵向分步骤”的统一裁决模型。
2.2 “横向分类型,纵向分步骤”量化裁决模型
为了化简“棋子类型-任务环节-影响因素”较为复杂的3 层链式关系,本文将任务环节进一步细化成任务步骤,确保每一个任务步骤对应的影响因素是确定的且不多于3 个,即不同类型棋子相同的任务步骤对应的影响因素是相同的。例如,侦察卫星棋子的目标捕获步骤包含的影响因素与气象卫星棋子的目标捕获步骤包含的影响因素完全相同,这样两种类型的卫星棋子在目标捕获步骤就可以调用同一个函数。此即为“横向分类型,纵向分步骤”量化裁决模型。
基于此模型则不同类型的棋子执行任务就是不同任务步骤的有序组合。因此,在裁决系统中不用针对每种类型的棋子编写量化裁决模型,只要针对所有的任务步骤编写量化裁决模型即可,在对某种类型棋子的任务执行过程进行量化裁决时,只需要调用其相应步骤的裁决模型即可,其关系如图2所示。

图2 “类型-步骤”关系图
如图2 所示,共分出了从“目标探测”到“类型d效果”9 个裁决步骤,不同的裁决步骤经过有序组合,对应着不同类型棋子的任务执行过程。如地基类型a 棋子的裁决过程,可以按目标探测、目标捕获、闭环跟踪、类型a 攻防4 个步骤裁决,地基类型b 棋子的裁决过程,可以按目标探测、目标捕获、闭环跟踪、末端制导、类型b 攻防5 个步骤裁决。因此,卫星棋子的裁决模型只需要按如上裁决步骤编写量化裁决模型即可,有效简化了量化裁决模型的编写,且后续若有新类型的棋子加进来,只需要根据其类型有序调用对应的裁决步骤序列即可,若现有量化裁决模型库里的裁决步骤不能完全满足新类型棋子的过程裁决,可以往裁决库里加入新的裁决步骤。
“横向分类型,纵向分步骤”量化裁决模型与“棋子类型-任务环节-影响因素”3 层链式模型相比,模型库更加精简和模块化,在后期的维护和扩容方面也更方便。
3 概率裁决模型——“三维概率裁决表”
传统兵棋在每个环节的裁决中因其影响因素简单,易于求出量化总值,故其概率裁决表也较为简单,表1 为某传统兵棋近战环节的概率裁决表[1]。
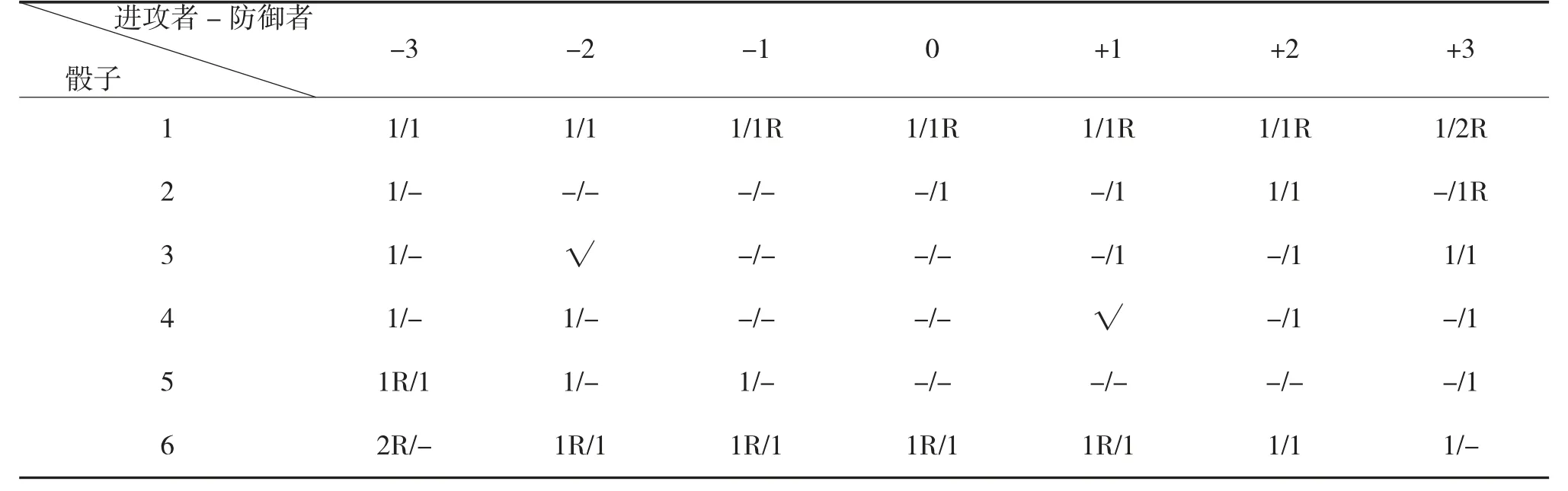
表1 近战裁决表
该近战环节影响因素为进攻者攻击力和防御者防御力,横轴影响因素量化总值为进攻者减去防御者,纵轴为骰子值,中间为裁决结果。从表中可以看出其影响因素简单,影响因素量化总值只需要加减即可[4]。空间兵棋影响因素类型多种多样,例如目标探测步骤,其影响因素有太阳高度角、太阳目标装备夹角、目标亮度、云层、风速,因目前空间领域相关的历史经验数据缺乏,难以通过科学合理的模型去求解各种类型影响因素的量化总值。因此,传统的概率裁决表模型对空间兵棋不适用。
本节针对此问题,提出了“三维概率裁决表”概率裁决模型。
“三维概率裁决表”中3 个维度x,y,z 代表影响因素的量化值,每个小立方体里都有一个概率值,当知道x,y,z 的值时,就可通过查表得出对应小立方体里的概率值,如图3 所示。例如在某个步骤量化裁决中,得出x,y,z 3 个影响因素的量化值为(1,1,1),则只需从三维概率裁决表中读取离原点最近的小立方体里的概率值,即为此步骤的裁决概率。量化值的取值范围切分的越细即小立方体分的越多,概率值越精确。

图3 三维概率裁决表
若某些裁决步骤影响因素多于3 个,则可以将此裁决步骤进一步细分,保证每个裁决步骤最多有3 个影响因素,若裁决步骤影响因素为两个,则“三维概率裁决表”z 轴取值为0,降为二维进行概率裁决。同理,若影响因素只有一个,降为一维进行概率裁决。因此,“三维概率裁决表”相对一维二维向下兼容,则对所有的裁决步骤可以建立统一的概率裁决模型。
概率裁决表是通过统计分析大量的历史经验数据获得,而空间兵棋对于我国来说,是一个新兴领域无历史数据可用,只能人为设计概率计算模型,靠仿真打靶得到大量的仿真数据,再对仿真数据进行统计分析,进而得到概率裁决表,其过程如图4 所示。

图4 仿真打靶流程
三维概率裁决表中每个小方块内概率值是由其对应影响因素取值范围内打靶成功率获得的。例如 统 计 影 响 因 素 取 值x ∈(0,2),y ∈(0,2),z ∈(0,2)时,总的试验次数N 和打靶成功的次数n,则三维概率裁决表对应小方块里的概率值为:

当空间兵棋的量化裁决模型和概率裁决模型都建立起来后,其裁决流程如图5 所示。
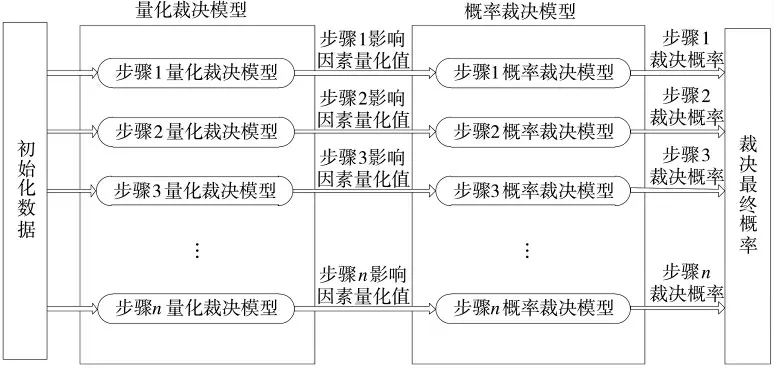
图5 空间兵棋裁决流程
利用“横向分类型,纵向分步骤”量化裁决模型求出各步骤中影响因素的量化值,再将影响因素的量化值输入各步骤的概率裁决模型,得到各步骤的裁决概率,最终得到某类型棋子整个任务执行过程的裁决结果。
4 仿真算例与分析
本节设计算例将含有5 个影响因素的目标探测步骤进一步细分为各含有最多3 个影响因素的步骤a 和步骤b,对比裁决结果,检验了纵向分步骤量化裁决模型的合理性。又以步骤a 为例,将三维概率裁决表与概率计算模型的裁决结果进行了全面直观的对比,证明了三维概率裁决表的有效性。
4.1 利用大量仿真数据统计制作三维概率裁决表
对步骤a 进行仿真,统计仿真数据制作三维裁决概率表。其中步骤a 包含太阳高度角,太阳目标装备夹角和目标亮度3 个影响因素。
三维概率裁决表中x 轴为q1归一化后的量化值,y 轴为q2归一化后的量化值,z 轴为q3归一化后的量化值。为了方便呈现,将步骤a 的三维概率裁决表展开如表2~表6 所示。

表2 x 为0~2

表3 x 为2~4

表4 x 为4~6

表5 x 为6~8

表6 x 为8~10
对步骤b 进行仿真,统计仿真数据制作三维概率裁决表。其中步骤b 两个影响因素的量化值分别为q1(云层)和q2(风速)。
三维概率裁决表中x 轴为q1的量化值,y 轴为q2的量化值,z 轴值恒为0。因为z 轴恒为0,因此,三维概率裁决表自动降为二维,如表7 所示。

表7 z 为0
4.2 检验纵向分步骤的有效性
利用概率计算模型计算包含5 个影响因素的目标探测步骤的裁决结果,再利用概率裁决表查找步骤a 和步骤b 的裁决结果,通过对比来证明将多于3 个影响因素的裁决步骤进一步细分的方法是有效的。
蓝方初始数据:
1)裁决初始时刻(北京时):2019-06-19 日8:32'00'';
2)地面装备位置(纬经高):(N28.12°,E112.59°,45 m)。
红方初始数据:
1)卫星初始轨道根数:(6 671 140;0.000 1;34.5°;0°;3°;240°);
2)卫星亮度:3。
环境配置数据:
1)云层:2;
2)风速:4。
由量化裁决模型,求出目标探测步骤5 个影响因素量化值:
q1=53.291 7°q2=11.870 5°q3=2 q4=7 q5=4
由概率计算模型,得目标探测步骤概率:
p0=0.309 815
将目标探测步骤分为步骤a 和步骤b:
1)步骤a 3 个影响因素量化值:
q1=53.291 7°q2=11.870 5°q3=2
3 个影响因素量化值分别归一化得“三维概率裁决表”中x,y,z 值:x=5.921 3,y=0.659 471,z=2。查询三维概率裁决表(表4),得步骤a 裁决概率:
pa=0.81
2)步骤b 两影响因素量化值:
q4=7 q5=4
两个影响因素量化值分别归一化得“三维概率裁决表”中xyz 值:x=7,y=4,z=0。查询三维概率裁决表(表7),得步骤b 裁决概率:
pb=0.355 469则步骤a 和步骤b 裁决得最终结果:
pa*pb=0.287 930
由结果可知目标探测步骤未拆分前,由概率计算模型计算得的结果0.309 815 与拆分成步骤a 和步骤b 后,由三维概率裁决表裁决的结果0.287 930非常接近。因此,可知将影响因素个数大于3 个的步骤经过进一步细分,进而由三维概率裁决表进行裁决是可行的。
4.3 检验三维概率裁决表的合理性
为了更加全面直观地比较“三维概率裁决表”与概率计算模型的裁决结果,以步骤a 为例,将3 个影响因素量化值q1,q2和q3归一化后从0~9 取值,求裁决结果,进行比对。
如图6 所示,横轴代表步骤a 3 个影响因素q1,q2和q3分别从0~9 进行取值,纵轴是3 个影响因素的取值对应的概率值。蓝色曲线为概率计算模型裁决结果,绿色曲线是“三维概率裁决表”裁决结果。

图6 裁决结果图
比较以上结果可知,“三维概率裁决表”的裁决结果与概率计算模型计算出的裁决结果基本吻合,即与仿真结果基本吻合,也就是说由大量仿真数据统计得来的三维概率裁决表,能较为完整地反映仿真模型的特点。因此,有理由相信,在未来由大量的真实数据统计得来的“三维概率裁决表”的裁决结果,也能较为完整地反映真实事件特性。
5 结论
传统兵棋在量化裁决中影响因素的简单量化,和概率裁决中影响因素量化总值的简单求解,并不适用于影响因素复杂多样的空间兵棋,因此,本文针对空间兵棋的特点,提出了“横向分类型,纵向分步骤”量化裁决模型和“三维概率裁决表”概率裁决模型,并通过算例验证了两种模型的可行性。因“三维概率裁决表”模型中,小方块越多,即表格切分的越多,则取值越精确,但相应的计算量也会增加,如何平衡精确取值和减少计算量,将是后续研究的重点。

