GRAPES-GEPS全球集合预报系统湿奇异向量的时空尺度敏感性研究

王静 刘娟娟 王斌 陈静 刘永柱

1 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室（LASG），北京 100029

2 国家气象中心，北京 100081

3 中国科学院大学，北京 100049

1 引言

奇异向量（Singular Vectors，简称SVs）初值扰动方法是当前主流的集合预报初值扰动方法之一。依据线性动力学中的有限不稳定理论，利用切线性模式（Tangent Linear Model，简称TLM）和伴随模式（Adjoint Model，简称ADM），在特定的约束条件下得到的SVs反映了相空间扰动增长最快的方向，由这些SVs构成的集合预报初始扰动代表了大气误差的分布特征（Lorenz,1965;Molteni and Palmer,1993;Buizza and Palmer,1995,1998;Molteni et al.,1996;Buizza et al.,1999）。20世纪90年代，欧洲中期天气预报中心（European Centre for Medium Range Weather Forecasts，简称ECMWF）率先将SVs应用于全球集合预报系统进行初值扰动（Palmer et al.,1993;Molteni et al.,1996），在此之后日本气象厅、法国气象局和澳大利亚气象局也开展了基于SVs初值扰动的集合预报系统研究（Diaconescu and Laprise,2012）。中国气象局数值预报中心自2008年起开始研发基于GRAPES (Global/Regional Assimilation and Prediction System)模式（陈德辉和沈学顺,2006;薛纪善和陈德辉,2008）的SVs初值扰动技术。刘永柱等（2013）基于GRAPES全球TLM和ADM1.0版本开展了SVs方法研究，受限于TLM和ADM发展技术，该初值扰动方案存在一些不足，如扰动能量在近地面迅速增长、SVs计算效率较低等。李晓莉和刘永柱（2019）研究了GRAPES全球奇异向量的改进方案，在全球TLM和ADM2.0模式中引入了线性化边界层物理过程，该方案能够有效解决上述问题并且提高计算效率。目前业务运行的全球集合预报系统（Global Ensemble Prediction System, 简称GEPS）副热带地区SVs的计算使用TLM和ADM2.0版本，引入线性化边界层方案，使用总能量模为权重算子，水平分辨率为2.5°，最优化时间间隔（optimization time interval，简称OTI）为48小时，并采用初始奇异向量与演化奇异向量相结合的方式构建初始扰动。

SVs的扰动结构与模式水平分辨率、权重模、OTI的长短以及切线性模式和伴随模式中线性化物理过程的使用密切相关（Diaconescu and Laprise,2012）。Komori and Kadowaki（2010）在研究热带地区的SVs时，发现提高模式水平分辨率后小尺度的信息表现得更加清晰。Buizza and Palmer（1998）使用了三种水平分辨率（T21、T42和T63）计算副热带地区的SVs，研究发现更高分辨率的T42和T63对模式误差的预报较好，指出高分辨率的切线性模式也需要更多线性化物理过程。线性化物理过程即在切线性模式中对预报模式中的物理过程进行线性化处理，使切线性模式能够包含更多的物理信息。国际上一些学者将在切线性模式中使用与降水过程有关的线性化湿物理过程方案（如线性化的大尺度凝结方案和线性化积云对流参数化方案）来计算得到的SVs称为湿奇异向量（Moist SVs，简称MSVs），反之称为干奇异向量（Dry SVs，简 称DSVs；Coutinho et al.,2004；Hoskins and Coutinho,2005；Diaconescu and Laprise,2012）。

Buizza（1994）针对DSVs开展了最优时间间隔（OTI）分别为12～72 h的敏感试验，试验指出OTI为12 h与OTI为24～72 h的初始扰动有很大差异，OTI为12 h的试验不足以产生足够的扰动，认为OTI的最小值应当为24 h。Komori and Kadowaki（2010）使用干能量模的SVs研究台风时对比了24 h和48 h的OTI，认为48 h的演化时间对中纬度大尺度天气过程有更大的影响，而24 h的演化时间有利于热带气旋相关结构的快速发展。此外，Palmer et al.（2007）和Puri et al.（2001）等人的研究表明热带地区的SVs需要更高的模式水平分辨率、相对较短的OTI以及更多切线性物理过程。另一方面，Walser et al.（2006）使用TL96包含湿物理过程的切线性模式计算了MSVs，其中OTI为24 h，对比与ECMWF业务运行DSVs（分辨率T42，OTI为48 h）的差异，发现提高MSVs时空尺度能够在预报前期提供更可靠的离散度。

目前我国业务运行的GRAPES-GEPS在TLM和ADM中线性化物理过程仅使用了线性化边界层方案，其求得的奇异向量也是DSVs。随着GRAPES切线性模式和伴随模式的发展，有更多的线性化物理过程加入了模式中（刘永柱等,2017）。Wang et al.（2020）基于业务GRAPESGEPS在SV计算中引入了线性化大尺度凝结方案，分析了GRAPES模式中热带外地区MSVs的特征，而其OTI和水平分辨率设置与当前业务运行的DSVs版本相同。线性化湿物理过程的引入也带来了一定的挑战，因为提高SVs水平分辨率将有利于集合预报捕捉更小尺度的天气特征，而水平分辨率的变化进一步影响了切线性近似是否在OTI内成立。如何配置MSVs计算的时空尺度，使其既能保证MSVs计算中切线性近似的成立，又能捕捉更多更小尺度的初始扰动特征，这对其在集合预报系统中的应用至关重要。因此，在GRAPES-GEPS中开展MSVs的OTI和水平分辨率（时空尺度）的敏感性研究，是一项具有实际意义的工作。本文基于GRAPES-GEPS从能量模、能量谱、空间分布等方面分析不同时空尺度下副热带地区MSVs特征，期望为MSVs设置适宜的OTI和水平分辨率，既能保证MSVs的扰动能够得到充分的发展，同时还兼顾计算代价及稳定性。此外本文还将从集合预报的角度（等压面变量评分、降水评分，降水概率预报等）评估不同参数设置下集合预报的效果，分析MSVs扰动的非线性发展特点，期望为集合预报提供更好的初值扰动。

2 方案设计

2.1 SV计算方案简介

一个小扰动X从初始时刻t0到演化时刻t的变化可以用线性近似来表达：

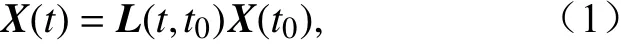
其中，L(t,t0)是向前的切线性算子，X(t0)为初始时刻的扰动，X(t)是演化时刻的扰动。SVs的求解可以归结为演化扰动向量与初始扰动向量模比值最大的问题：

其中，[,]为欧拉内积,下文将略去X(t)函数的括号，E为转化算子。

然后，将状态向量X从物理空间转变为欧拉空间的无量纲向量X˜：

根据能量模公式（李晓莉和刘永柱，2019），变换算子E可以表示为

式中，ρr为参考密度，cp为定压比热，Tr为参考温度，θr为参考位温，Пr为参考无量纲气压。

由此公式（2）可表达为

更为详细的介绍可以参考刘永柱等（2013）和李晓莉等（2019）。由SVs的计算过程可知，影响SVs结果的关键因素有三个：一是权重模的选取，许多研究表明，基于干能量模算子的SVs能够产生中纬度斜压不稳定的扰动（Hoskins and Coutinho,2005;刘永柱等,2013）；二是演化时间的选择，也就是OTI，目前中纬度DSVs的计算往往将OTI设置为48 h；三是切线性模式中的线性化物理过程的选择，目前GRAPES-GEPS业务版本中SVs计算过程使用的线性化物理过程仅包含垂直扩散和次网格尺度地形参数化，称为线性化边界层方案（Planetary Boundary Layer，简称PBL；李晓莉和刘永柱,2019）。由前人的研究可知线性化大尺度凝结过程对SVs有重要的影响（Zadra et al.,2004），因此GRAPES全球切线性模式也发展了大尺度凝结方案（刘永柱等,2019），该方案是基于Tompkins and Janisková（2004）提出的简化大尺度云和降水方案而开发的。本文针对该线性化湿物理过程计算得到的MSVs开展研究。

2.2 试验设置

叶璐等（2020）基于区域模式研究多尺度奇异向量初值扰动时提出可使用水平尺度为0.5°的SVs代表小尺度不确定信息、1.5°和2.5°则分别对应中尺度和大尺度。本文的研究基于全球模式，2.5°水平分辨率可以分辨出大尺度天气过程，而1.5°水平分辨率可用于分析中尺度天气过程。因此本文设计了2.5°和1.5°水平分辨率的对比试验，2.5°和1.5°水平分辨率对应的模式积分步长为1200 s、600 s，试验的目的是为了突出湿线性化物理过程对中尺度扰动的作用。提高水平分辨率无疑会增加计算成本，需要进一步调整参数，减轻计算代价。本文还将进行OTI敏感性试验，分别将OTI设置成24 h与48 h，为了保障SVs计算的稳定性及计算效率，相应的积分步长也做出调整，对比两种不同OTI设置对SVs的影响。

本文试验设置中，MSVs的物理过程包括线性化的垂直扩散、次网格尺度地形参数化和大尺度凝结线性化过程。试验R25t48（表1）表示水平分辨率为2.5°，OTI为48小时，这种时空分辨率设置与DSVs业务系统相同，其余几组试验名称以及具体的设置详见表1。

表1 时空分辨率对照试验的设置Table 1 Settings of horizontal resolution and OTI

本文的试验时段为2019年5月1日12:00至5日12:00（协调世界时，下同），共5天，预报时长240 h，预报间隔24 h，集合预报成员31个，非线性预报模式水平分辨率为0.5°。SVs的计算目标区域为北半球（20°N～80°N）和南半球（20°S～80°S）。由SVs构造扰动初值的计算方案参见李晓莉等（2019）和霍振华等（2020）。本文的SVs扰动初值仅考虑初始时刻SVs（Initial SVs），不包含演化时刻SVs（Evolved SVs）。此外，为了更清楚地描述初值扰动的作用，本文的试验均未开启模式扰动。

3 不同时空尺度下MSVs结构分析

3.1 能量模垂直分布

对四组试验的初始时刻及经过各自OTI线性积分的最后演化时刻（Evolved final time）SVs能量模垂直分布进行分析，图1为30个SVs的5天平均结果。无论OTI长短，初始时刻（图1a）MSVs的能量模大值区位于对流层中层（20层以上，约700 hPa以上），动能和内能分布相似，内能占比略多于动能。然而在20层以上，R25t24和R15t24的初始能量分别大于R25t48和R15t48，20层以下，R15t48的初始能量最大。SVs经过切线性模式积分到最后演化时刻，由图1b可见，动能与内能的增长趋势基本保持一致，但动能增长更大，占据总能量的主导地位，且高层增加更明显。OTI为24h的R25t24（红色线）和R15t24（蓝色线）试验的能量模集中在20～40层之间，能量从初始时刻到最后演化时刻向上传播的趋势更明显，且高分辨率的R15t24能量大于低分辨率的R25t24。值得注意的是，R15t24在18层左右有能量的陡增，这是由于在试验时段内个别SVs在低层迅速增长，这种陡增在增加试验天数之后能够得到平滑。而OTI为48 h的R25t48与R15t48相对于初始时刻都出现了明显的能量下传，且由于演化时间较长，整个对流层的能量都有所增加。

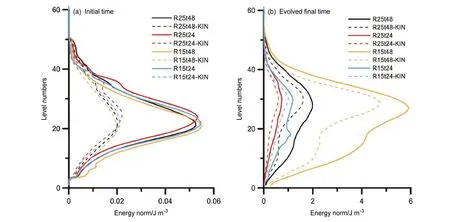
图1 （a）初始时刻及（b）最后演化时刻的能量模垂直分布（虚线表示动能KIN，实线表示总能量）Fig.1 Vertical distributions of energy norm at(a) the initial time and(b) the evolved final time.The dashed lines indicate the kinetic energy(KIN),and thesolid linesindicatethetotal energy

总的来说，SV计算的水平分辨率越高，OTI时间越长，最后演化时刻能量模越大。采用较长OTI得到的MSVs在最后演化时刻低层能量有一定增长，能量存在明显的下传，而OTI时间较短的MSVs能量的上传更为明显。

3.2 能量谱分析

图2展示了30个MSVs在第26层（约500 hPa）5天平均的能量谱分布。首先分析初始时刻（图2a）能量谱，在2.5°水平分辨率下，OTI较短的R25t24相对于R25t48而言，能谱向中小尺度偏移，与此同时两者能谱峰值保持一致。而在1.5°水平分辨率下，OTI较短的R15t24不仅相对于R15t48向更小尺度偏移，其能谱的峰值也移动到30～40（约1000 km）波数处，而其余几组试验在20～25波数（约2000 km）左右。这说明采用较短的OTI可以在中尺度范围产生较大SVs扰动。在图2b中，所有试验的能谱峰值均在15～20波数左右，意味着能量从初始时刻到最后演化时刻有升尺度转移的特征，而高分辨率的R15t48相较于R25t48含有更多中尺度能量，表明水平分辨率的提高有利于能量向中尺度转移。

图2 （a）初始时刻及（b）最后演化时刻奇异向量SVs在第26层（约500 hPa）能量谱（单位：10−9 J kg−1）Fig.2 Energy spectrum (units:10−9 J kg−1) of SVs (Singular Vectors)at level 26(about 500 hPa)at (a)theinitial timeand (b)theevolved final time

总的来说，采用较短的OTI和提高MSVs水平分辨率可以在中尺度范围产生较大SVs扰动。

3.3 初始时刻MSVs水平分布

将四组试验5月1日12:00初始时刻第26层（500 hPa）前15个MSVs叠加，图3为SVs扰动位温和控制预报12:00 500 hPa位势高度场分布图。由图3可见几组试验主要的扰动都分布在斜压不稳定的区域，如东亚大槽前后，欧洲前槽以及北美槽处，然而MSVs的形态和大小均有所不同。以东亚槽区（图3中红色圈）为例，R25t48在东亚槽后的MSVs较小，而缩短OTI的R25t24覆盖了整个东亚地区。在提高水平分辨率之后，MSVs的尺度明显减小（图3c和d）。较短OTI的R25t24（图3b）和R15t24（图3d）中扰动的正负对均匀分布，且它们的扰动量分别大于R25t48和R15t48，这与能量模垂直分布的结论是吻合的，即20层以上，较短OTI的MSVs的初始时刻能量更大。

图3 （a–d）四组试验初始时刻（5月1日12:00，协调世界时，下同）北半球前15个MSVs在第26层（约500 hPa）扰动位温（填色，单位：10−3 K）水平分布，黑色线为控制预报500 hPa位势高度Fig.3 Perturbed potential temperature(shaded,units:10−3 K)of the first 15 MSVs in the Northern Hemisphere at level 26(about 500 hPa)at the initial time(1200 UTC 1 May)in (a–d) the four numerical experiments.The black solid line indicatesthe 500-hPa geopotential height with controlled forecast

总的来说，在R25t24和R15t24两组试验中，东亚槽区的SVs扰动与环流场吻合的程度高于其他两组试验，且其形态分布与位势高度曲线近乎垂直。提高水平分辨率使初始SVs具有更多中小尺度信息。同一水平分辨率下不同OTI所产生的MSVs结构有很大的差异，下一节将对此进行相关性分析。

3.4 不同OTI下MSVs相似性分析

为了进一步了解不同OTI下MSVs的结构差异，对同一水平分辨率不同OTI的MSVs进行相似性分析，对某一变量的水平分布做相关系数R：能在对比试验中找到与之相似度较高的结果（时间步长为1200 s的SV01与时间步长为600 s的SV08匹配度较高，限于图表大小未能显示），也就是说，时间步长的影响使SVs的排序出现偏差，但总的结果是相似的，由此可以说明，时间步长的对MSVs结构分布的影响较小。在此基础上，将积分步长控制为1200 s，水平分辨率设置为1.5°，将OTI分别为24 h和48 h的两组试验进行对比分析，结果如表5所示，不同OTI的MSVs之间相似性很低。因此R25t48（R15t48）与R25t24（R15t24）SVs的结构变化主要是由于OTI不同造成的，而非时间积分步长。

表5 OTI分别为24 h和48 h的两组试验相似性对比Table 5 Similarities of the two experiments at different optimization times of 24 h and 48 h

表2 R25t24与R25t48前5个MSVs第20层的纬向风扰动相似性Table 2 Similarity of R25t24and R25t48（Zonal wind disturbance of the first 5 MSVs at level 20）

表3 R15t24与R15t48前5个MSVs第20层的纬向风扰动相似性Table 3 Similarity of R15t48 and R15t24（Zonal wind disturbance of the first 5 MSVs at level 20）

表4 时间步长分别为600秒和1200秒的两组试验相似性Table 4 Similarity of the two experiments with 600s and 1200s integration timesteps

4 集合预报结果分析

在上一节中，从能量模、能量谱、空间剖面等方面分析了在不同时空分辨率下MSVs的特征，这里进一步利用这些集合扰动样本进行预报，以评估不同试验计算得到的扰动对集合预报效果。

4.1 集合平均扰动能量随预报时间的增长特征

Palmer et al.（1998）定义了一个集合扰动总能量为

图4为5天平均的集合平均扰动能量随预报时间的增长特征，红色线代表OTI为24 h的SVs构成扰动初值的预报，黑色线代表OTI为48 h的预报。初始时刻（图4a）低分辨率的两组试验扰动能量非常接近，高分辨率的两组试验扰动能量差异较大，同一分辨率下OTI越短初始扰动能量越大。与此同时，R25t24（红色实线）的初始扰动能量在400 hPa以下小于R15t48（黑色虚线），然而经过不同预报时间之后，R25t24的扰动增长明显大于OTI较长的R15t48和R25t48。由此可见，不同OTI所形成的初值扰动增长差异较大，采用较短OTI所构成的扰动初值的能量增长更大，尤其是在预报的前48 h。在预报的初始阶段（24 h），OTI同为48 h的R25t48和R15t48差异较小，说明在OTI为48 h时，不同水平分辨率MSVs构成的初值扰动并未在预报24 h内体现出明显差异，即采用较长的OTI所构造的扰动初值不能代表短期预报的扰动增长特征。相比而言，预报阶段R15t24（红色虚线）的扰动增长在各个高度上都大于R25t24（红色实线），这表明提高MSVs水平分辨率之后，更有利于扰动能量的增长。

较短的OTI能捕捉到临近时段快速增长的扰动方向，它同时代表了未来一段时间内扰动的增长特征，也就是说它包含了较长OTI扰动的基本特征，同时较短的OTI更容易保证切线性近似的成立，使得SVs的计算更为准确。从中长期预报来看（图4d），R25t24与R15t48扰动几乎重合，从计算效率的角度上看，提高SVs的水平分辨率会增加计算负担，而缩短OTI能够减轻计算代价，所以，相比于R15t48，R25t24能够在不减小扰动能量的条件下减轻计算代价。

图4 不同预报时长集合预报5天平均扰动能量（单位：J kg−1）随高度的分布：（a）0 h；（b）24 h；（c）48 h；（d）120 hFig.4 Distributions of ensemble forecast on 5-day average perturbation energy(units:Jkg−1)with height at different forecast time:(a)0 h;(b)24 h;(c) 48 h;(d)120 h

4.2 集合预报要素评分

4.2.1集合离散度、均方根误差及集合一致性

图5为四组试验不同变量的离散度（Spread）和均方根误差（Root Mean Square Error，简称RMSE）随时间的变化，左列为离散度，中间列为均方根误差，由图可见，OTI较短的两组试验（R15t24和R25t24）的离散度在预报的0～96 h有明显提升，其余时次各组试验各个变量离散度大体相当。而在同一OTI下，提高SVs水平分辨率也能使得离散度在前期有所增加。这与Walser et al.（2006）对MSVs的分析一致，即提高时空尺度后的MSVs能够在预报的初始阶段提供较好的离散度。图5d1中可以看到R15t24中2 m温度（T2m）的离散度在整个预报时次都有所增长。从均方根误差来看，R15t24的均方根误差在24～120 h有增加，除R15t24以外的三组试验中各变量的RMSE差异不大，说明提高SVs水平分辨率和缩短OTI对于集合预报RMSE来说并非绝对的正效益。集合一致性（Consistency）则指的是离散度与均方根误差的比值，集合离散度是否与均方根误差大致相当是衡量一个集合预报系统好坏的标准，一致性越接近于1，预报效果越好。从右列集合预报一致性检验可见，评分的主要差异体现在预报的前48 h。OTI为24 h（R15t24和R25t24）的MSVs形成的集合预报的一致性在48 h内明显提高了，且R15t24和R25t24对T2m改进的效果比其他变量更明显。

图5 离散度（左列）、均方根误差（中间列）以及集合一致性（右列）随时间的变化：（a1−a3）500 hPa纬向风（单位：m s−1）；（b1–b3）850 hPa纬向风（单位：m s−1）；（c1–c3)近地面10米纬向风（单位：m s−1）；（d1–d3）近地面2米温度（单位：°C）Fig.5 The spread(left column),root mean square error(RMSE; middle column),and consistency(right column)over time:(a1–a3)Zonal wind of 500 hPa (units:m s−1);(b1–b3)zonal wind of 850 hPa (units:m s−1);(c1–c3)10-m zonal wind near theground (units:m s−1);(d1–d3)2-m temperature near theground (units:°C)

4.2.2集合预报outlier评分

图6为四组试验的outlier评分，其值越小，说明集合预报结果越可靠，概率预报越准确。由图可见，四组试验的outlier 值随预报时间都呈减小趋势，但相比而言，OTI为24 h的MSVs集合预报结果（R25t24和R15t24）具有更小的outlier值，这种优势在预报的前48 h表现得尤为明显。综合上一节的分析结果，R25t24和R15t24两组试验的初期离散度增加的同时outlier值减小，说明集合成员间更加发散且观测能够更大概率落在集合成员之间。提高SVs计算分辨率后，在预报的前48 h内，R15t24的outlier评分略逊于R25t24，但仍然优于OTI为48 h的R25t48和R15t48。低层变量outlier评分差异较小，高层变量outlier评分差异较大。

图6 四组试验的集合预报outlier评分：（a）500 hPa纬向风；（b）850 hPa纬向风；（c）近地面10米纬向风；（d）近地面2米温度Fig.6 Outlier scores of the ensemble forecast:(a) Zonal wind of 500 hPa;(b)zonal wind of 850 hPa;(c)10-m zonal wind near the ground;(d)2-m temperature near the ground

以上的分析说明了MSVs需要的OTI更短，这与Coutinho et al.（2004）及Hoskins and Coutinho（2005）等的分析一致。然而，从全球集合预报的角度来看，提高SV计算水平分辨率并不一定能有效提高集合预报outlier评分。

4.2.3 2 m温度的离散度空间分布

图7给出了为四组试验北半球24 h预报的T2m的离散度空间分布。由图7可见四组试验集合离散度较大的区域主要在陆地。相比而言，OTI较短的R25t24和R15t24形成T2m集合预报的离散度大于R25t48和R15t48，说明OTI较短的两组试验的集合预报在低层变量上有较大的离散度。将MSVs的水平分辨率提高之后，R15t24的2 m温度的离散度相比于R25t24进一步增大。这说明对于低层变量而言，缩短OTI和提高水平分辨率都有利于离散度的增加。。

图7 （a–d）四组试验北半球2 m温度的集合离散度水平分布（填色，单位：°C）Fig.7 Horizontal distribution of the spread(shaded,units:°C)of 2-m temperature in the Northern Hemisphere in(a–d)the four numerical experiments

4.3 降水集合预报

4.3.1降水概率

2019年5月4～5日在中国华南地区有一次降水过程（图8a），主要降水位于广东东部、福建西南部地区，出现了50 mm暴雨量级的降水，甚至个别站点降水达到100 mm以上。四组试验初始日期为5月1日12:00，分析其对5月4日（即96 h预报）24 h累计降水的概率预报结果，图8b–e为四组试验降水量级大于25 mm的降水概率，四组试验对这次降水过程都有体现，只是在降水落区上稍有偏北，R25t48的降水概率较小，而其余几组试验的降水概率都有所增加，R15t24的降水概率大值区的分布大于R25t24和R15t48。说明提高MSVs的水平分辨率和缩短OTI之后所构造的扰动初值能够形成更好的降水概率预报结果。

图8 2019年5月4～5日（a）24 h累计实况降水量（单位：mm）分布及（b–e）四组试验大于25 mm量级降水的概率预报分布Fig.8(a)The distribution of 24-h cumulative observed precipitation and (b–e) the distribution of the probability forecast of precipitation greater than 25 mm in the four numerical experimentsfrom 1200 UTCMay 4 to 1200 UTC May 5,2019

4.3.2降水评分

分级降水集合预报相对作用曲线面积(Area under the relative operating characteristic curve,AROC)的评分越接近于1越好，由图9a和b可见，在预报的24～96 h内，对于小雨到中雨量级的降水而言，OTI为24 h的R25t24和R15t24的AROC评分基本上都高于OTI为48 h的R25t48（72 h除外）和R15t48，但提高水平分辨率反而使降水评分降低了。布莱尔评分（Brier Score）越小越好，由图9c、d可见R25t24在24～96 h小雨到中雨量级的降水评分是最好的，同一分辨率下，OTI越短评分越好，但是提高水平分辨率并未能提升小雨到中雨量级的降水评分。

图9 四组降水集合预报的（a、b）AROC（相对作用曲线面积）评分及（c、d）Brier降水评分：（a、c）10 mm降水量级；（b、d）25 mm降水量级Fig.9(a, b)AROC(Area under the Relative Operating characteristic Curve) precipitation scores and(c,d)Brier Scores of the four numerical experiments:(a,c)10-mm precipitation;(b,d)25-mm precipitation

5 结论

本文基于中国气象局数值预报中心自主研发的GRAPES-GEPS模式，针对引入湿线性物理过程后的MSVs，开展了时空尺度敏感性试验，从能量模、能量谱、空间分布等方面分析不同时空尺度下MSVs特征，并从集合预报的角度（等压面变量评分、降水评分、降水概率预报等）评估不同参数设置下集合预报的效果。结论如下：

从SVs结构变化的角度来看，提高MSVs计算的分辨率可使其具有较大的增长率，且可以产生新的SVs结构，这种结构分布在中纬度斜压不稳定的区域。不同OTI下初始MSVs相似性较低，结构差异较大。OTI为24 h和48 h试验从初始时刻到最终演化时刻有向上传播的趋势，且OTI为48 h的试验还出现了能量下传。从能量谱的角度来看，采用较短的OTI可以在中尺度范围产生较大SVs扰动。

进一步从集合预报的效果来评估，结果表明提高MSVs的水平分辨率和缩短OTI之后所构造的扰动初值能够提高近地面要素短期预报的离散度，并形成更好的降水概率预报结果，然而仅提高MSVs的水平分辨率并不一定能够改善等压面变量集合预报outlier评分。同一水平分辨率下，OTI越短降水评分越好。从计算效率的角度上看，提高SVs计算的水平分辨率会增加计算负担，而缩短OTI能够减轻计算代价。

但需要指出的是，本文基于5天的试验分析了不同时空尺度设置下MSVs的特征及集合预报结果，由于全球切线性伴随模式计算量较大，本文在SVs水平分辨率上仅设计了2.5°和1.5°两组对比试验,没有进行更精细化尺度的对比分析。通过分析可知，MSVs对于中小尺度短临天气系统能够有较好的指示意义，因此，下一步研究可以通过提高区域模式水平分辨率计算MSVs，并分析其对于高影响天气过程集合预报的效果。