强震作用下黄土隧道洞口段地震动放大效应研究

孙 文,梁庆国,刘青霞,孙纬宇

(1.兰州交通大学土木工程学院,甘肃 兰州 730070;2.甘肃省建设投资(控股)集团有限公司,甘肃 兰州 730050)

0 引言

我国西部黄土地区在公路与铁路建设中,桥隧占比较高,并且许多隧道在高烈度设防区。地震波由下往上的传播中在坡面与洞口处发生反射与折射[1],造成洞口段的动力响应增强,因此隧道洞口段是隧道抗震薄弱段[2-5],是众多学者对隧道动力响应与抗震性能关注的主要部位[6-9]。隧道洞口段概括而言应该包括两个部分:洞口周边的仰坡土体与沿隧道进深方向一定长度的衬砌结构。对洞口周边的仰坡土体而言,由于衬砌的存在改变了原有应力场的分布和土体间的变形接触关系,土与衬砌结构间形成了“土-结”相互作用体系,因此其动力易损性随之受到影响。汶川地震大量的实际震例表明,仰坡的失稳造成洞口段的掩埋和洞门的坍塌是洞口段地震失稳的主要震害之一[10-11],因此研究仰坡的动力响应规律、失稳破坏特点与易损区范围对于隧道洞口段的抗震设防和加固有重要意义。

坡面动力易损区的范围、隧道抗震设防长度与边坡高度[12]、角度[13]及隧道的入洞高程[14]有关:隧道在穿越沟谷地区时,涉及隧道入洞高程不同的问题。入洞高程的变化主要是涉及到隧道埋深的变化以及洞口引起的动力放大位置的改变,因此隧道边坡的高程放大效应以及隧道的抗震设防长度的变化需要结合隧道的进洞高程进行具体的讨论。黄土是一种具有大孔隙、弱胶结物性的特殊土[15],地质结构较松软,阻尼比较大,导致地震波在不同高度的黄土边坡中进行传播时,土体对其滤波作用不同,形成了边坡动力响应规律的差异。因此探究黄土隧道的洞口段放大效应需要结合边坡的高度进行探讨。有研究表明[16]洞口段的截面变形随坡度的增加而增大。据黄润秋等[17]通过对汶川地震震后地质灾害遥感统计分析发现,地震滑坡的优势坡角为20°～50°。对黄土山岭隧道而言,因受黄土垂直性的影响,其穿越的边坡普遍较陡,且地震常伴随降雨,地震与降雨耦合作用下黄土边坡会发生塑性流动和液化流滑,使得其在更小的角度下就会发生滑坡现象,因此黄土地震动滑坡的角度覆盖范围较广。

综上所知,研究强震作用下隧道洞口段地震动放大效应需结合边坡高度、角度与隧道入洞高程等影响因素进行探讨。本文采用数值计算的方法,研究兰州人工地震波作用下的黄土隧道仰坡沿高程方向与沿坡面水平方向的加速度、位移与应力变化规律,并进一步探讨沿隧道进深方向的衬砌地震动响应规律,提出仰坡的抗震加固范围与隧道衬砌加固长度建议值。研究结果有助于提高黄土隧道洞口段抗震加固的有效性和合理性。

1 模型简介

1.1 模型参数

采用迈达斯GTS有限元软件,分别设立边坡高度H为60 m、75 m与90 m,仰坡角度α为60°的变边坡高度模型;边坡高度为75 m,仰坡角度为45°、60°与75°,隧道在0.33倍坡高处入洞的变坡角入洞模型;以及边坡高度为75 m,坡角为60°,隧道在0.66倍坡高处入洞的模型。隧道洞径为13.3 m,二衬厚度为0.5 m,初衬厚度为0.35 m。以边坡高度为75 m,仰坡角度为60°,以隧道相对高程在h=0.66倍坡高处入洞的模型为代表,其网格划分如图1所示。

图1 带网格模型示意图(H=75 m,α=60°,h=0.66H)Fig.1 Schematic diagram of model with grid (H=75 m,α=60°,h=0.66H)

边坡土体为摩尔库伦模型,隧道衬砌为弹性模型,边界为弹塑性边界。围岩与隧道结构的主要物理力学参数如表1所列。

表1 模型材料物理力学参数Table 1 Physical and mechanical parameters of model material

1.2 地震波的选取

由于缺少黄土地区实测地震波数据,因此,基于兰州地区的场地条件,根据国家标准,采用随机振动理论,合成兰州人工地震波进行数值模拟,该地震波峰值加速度为264 gal,持时30 s,反应谱特征周期为0.32 s,其时程曲线如图2所示。

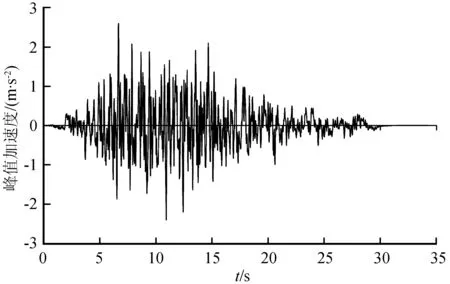
图2 地震波时程曲线Fig.2 Seismic wave time history curve

2 隧道的存在对坡面高程放大效应的影响分析

对不同高度、不同坡角、不同入洞高程模型沿坡面高程方向的加速度峰值与位移峰值进行提取分析,探究隧道洞口的存在对坡面高程放大效应的影响。

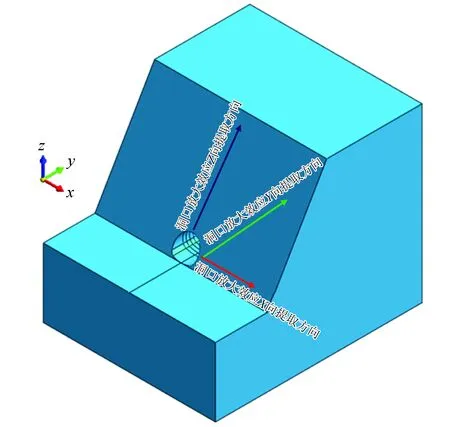
图3 洞口段放大效应提取方向示意图Fig.3 Schematic diagram of extraction direction of amplification effect in portal section

图4(a)为隧道在坡底处入洞时不同坡高模型的坡面加速度随高程的变化曲线,其中“h/H”为相对高程。由图4(a)可知,当隧道在坡底处入洞时,坡面加速度随着坡面高程的增加呈现先增大后减小的变化趋势。分析坡面加速度峰值位置与边坡高度知,坡面加速度的峰值高程点与坡高呈反比,即边坡越高,坡面加速度峰值高程点越低。

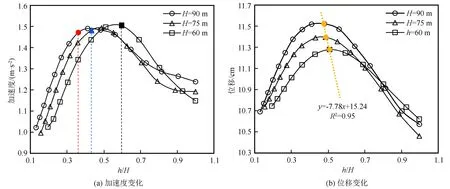
图4 不同坡高模型沿高程方向加速度、位移变化曲线Fig.4 Acceleration and displacement curves of models with different slope heights along the elevation

图4(b)为隧道在坡底处入洞时不同坡高模型的坡面位移随高程的变化曲线。由图4(b)可知,位移的变化趋势与加速度变化趋势类似,坡面位移峰值与其高程呈一阶线性关系。

不同坡度模型的坡面加速度、位移沿高程方向的变化规律如图5所示。由图5知,当隧道在0.33倍的坡高处入洞时,在隧道的高程两侧加速度与位移随着距洞口距离的增加呈先增大后减小的变化趋势,即在隧道的近端加速度和位移有一定的减小,这与传统的认为隧道的存在会引起土体的动力响应放大不同。分析这种现象产生的原因:隧道的存在改变了围岩原本的约束状态,由于衬砌相对于围岩刚度的增加,在土-结相互作用下,隧道结构对附近围岩形成了一定的约束作用,使隧道沿高程方向土体的变形减小,因此在隧道周围有一定范围的“自加固”区。

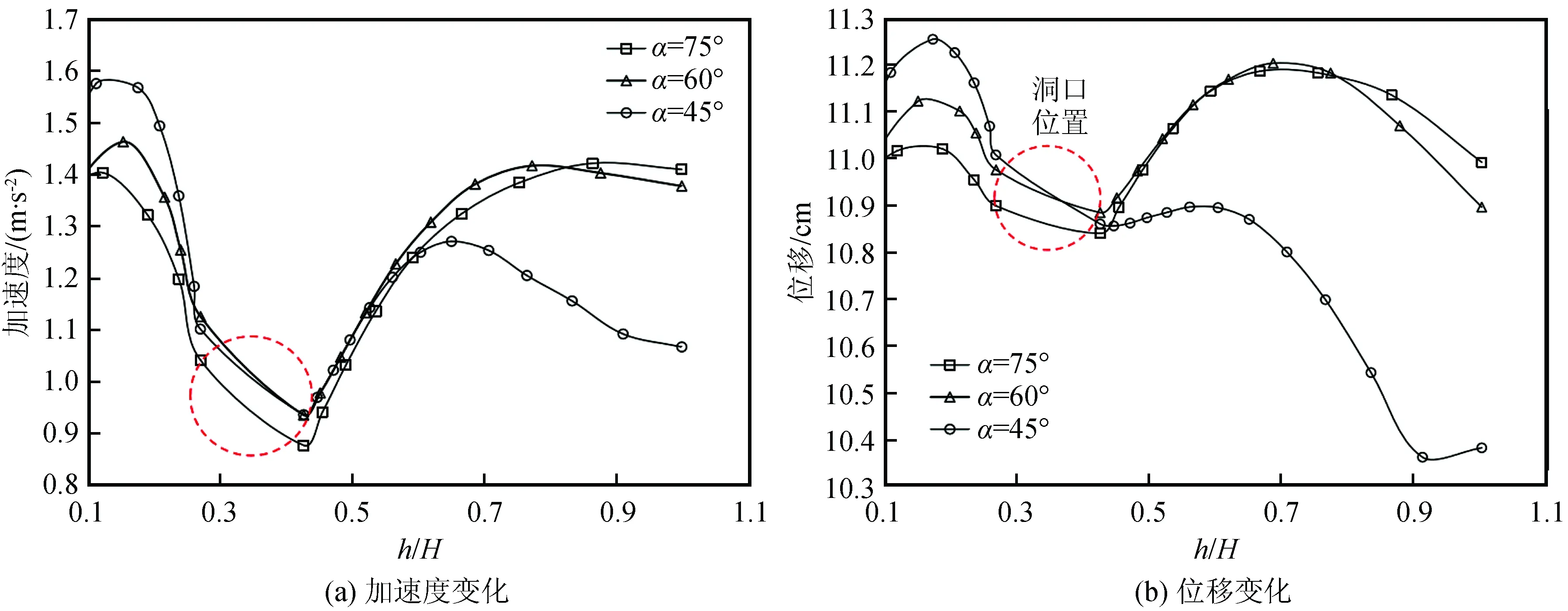
图5 不同仰坡角度模型沿高程方向加速度、位移变化曲线Fig.5 Acceleration and displacement curves of models with different slope angles along the elevation

另外,由图5还可知,在坡底处,加速度与位移随着边坡坡度的增加而减小,而在坡顶处,加速度与位移却随着坡度的增加而增大,这说明缓坡易发生坡底处的剪切破坏,而陡坡易发生坡顶的拉破坏。

由图6知,当隧道在坡面不同高程处入洞时,加速度与位移在隧道洞口高程方向呈“不对称式分布”,且当入洞高程h/H≤0.33时,即在坡面的中下部入洞时,靠近坡底一侧的加速度和位移峰值小于靠近坡顶一侧;而当h/H=0.66时,坡底侧的加速度与位移峰值大于坡顶一侧。这说明入洞高程的改变影响了坡面加速度与位移的动力响应分布规律。

图6 不同进洞高程模型沿高程方向加速度、位移变化曲线Fig.6 Acceleration and displacement curves of models with different portal elevation along the elevation

综上所述,隧道的存在对坡面地震动高程放大效应有重要影响,沿高程方向隧道的存在对周围土体有一定的加固作用,存在一定范围的“自加固”区。通过对不同坡度模型的加速度与位移响应规律分析发现,缓坡易发生坡底处的剪切破坏,而陡坡易发生坡顶的拉裂破坏。随着边坡高度的增大,坡面位移峰值逐渐增大,峰值点的高程却逐渐降低,说明随着高度的增加,边坡的滑动破坏范围逐渐增大。

3 隧道周围土体的水平向地震动放大效应分析

在坡面,沿图3所示的x向提取坡面的加速度与位移,分析隧道周围土体的水平向地震动放大效应。加速度与位移指此点处的绝对综合加速度峰值与绝对综合位移峰值。

分析图7(a)知,隧道在坡底处入洞时,加速度随着距洞口距离的增大呈现“增大-减小-增大”的变化趋势:第一个增大的过程与坡面高程方向的变化原因一致,为隧道衬砌“自加固区”,第二个增大的过程为模型的边界效应所致。

图7 坡底处入洞时不同高度模型加速度、位移变化曲线Fig.7 Acceleration and displacement curves of models with different heights when the portal section is at the bottom of slope

分析图7(b)知,位移的变化趋势与加速度略有不同:随着距洞口距离的增大,位移呈现小幅增大后迅速减小,然后再增大的变化过程。迅速减小的过程为洞口段对坡面位移动力放大的结果,而增大段为模型边界效应所致。因此如果取减小段与增大段的拐点作为坡面水平向的动力放大区,则隧道在坡底处入洞时,坡面洞口段放大范围为2.1～2.7倍洞径,随着边坡高度的增高,坡面洞口段放大区逐渐减小。

由图8知,隧道在0.33倍坡高处入洞时,加速度和位移皆呈现:随着距洞口距离的增大,先小幅增大后迅速减小,然后再增大的变化规律。取迅速减小段与增大段的拐点作为坡面水平向的动力放大区,则隧道在0.33倍坡高处入洞时,加速度显示坡面洞口段放大范围为2.0～2.4倍洞径,位移显示放大范围为2.3倍洞径。

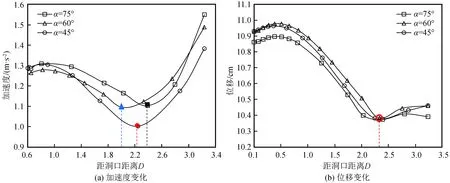
图8 h/H=0.33时不同坡度模型加速度、水平方向位移变化曲线Fig.8 Acceleration and horizontal displacement curves of models with different slope (h/H=0.33)

图9为三种入洞高程模型坡面水平方向加速度与位移变化曲线。分析可知:取边界放大效应与洞口放大效应相互影响的拐点定义隧道在坡面上的放大区知,加速度曲线显示不同入洞高程模型的坡面水平放大区为2.0D～2.8D,位移曲线则为1.0D～2.3D。结合坡面的应力分布来进一步对放大范围进行判定,如图10所示。

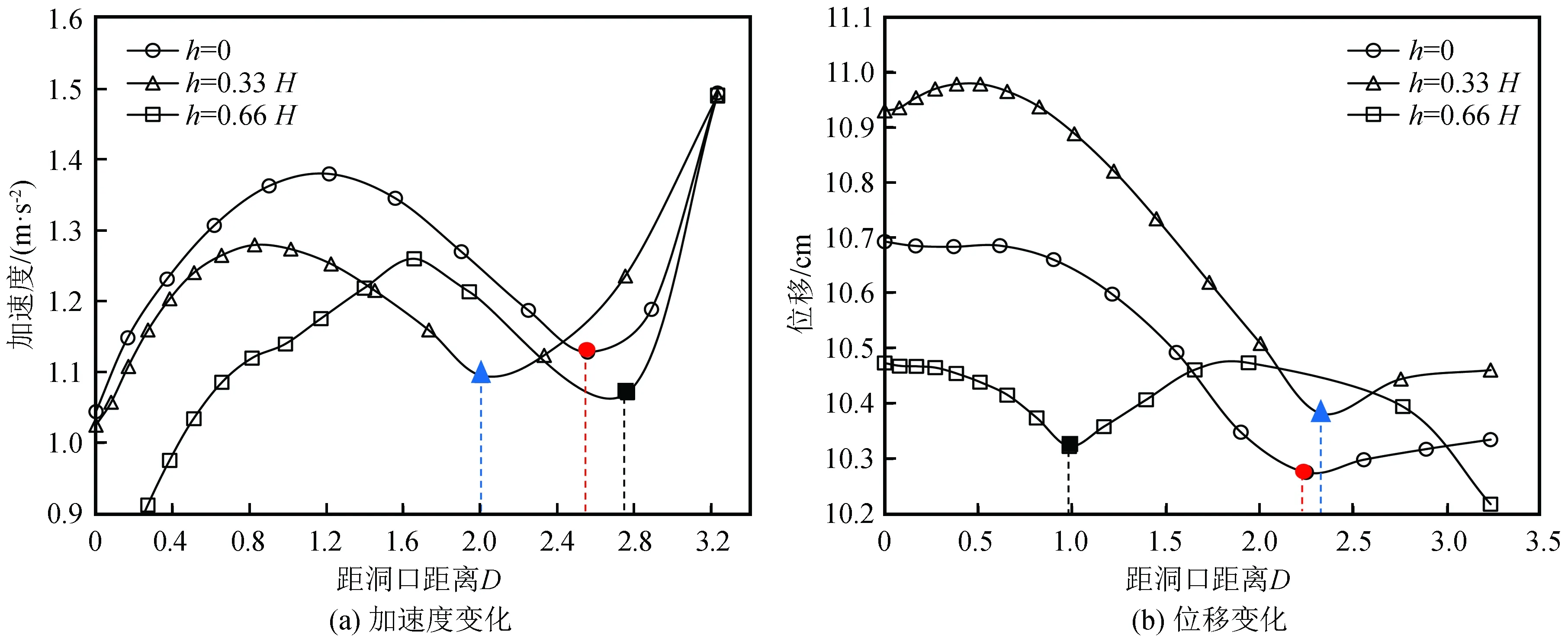
图9 不同入洞高程模型坡面加速度、位移变化曲线Fig.9 Acceleration and displacement curves on the slope of models with different portal elevation

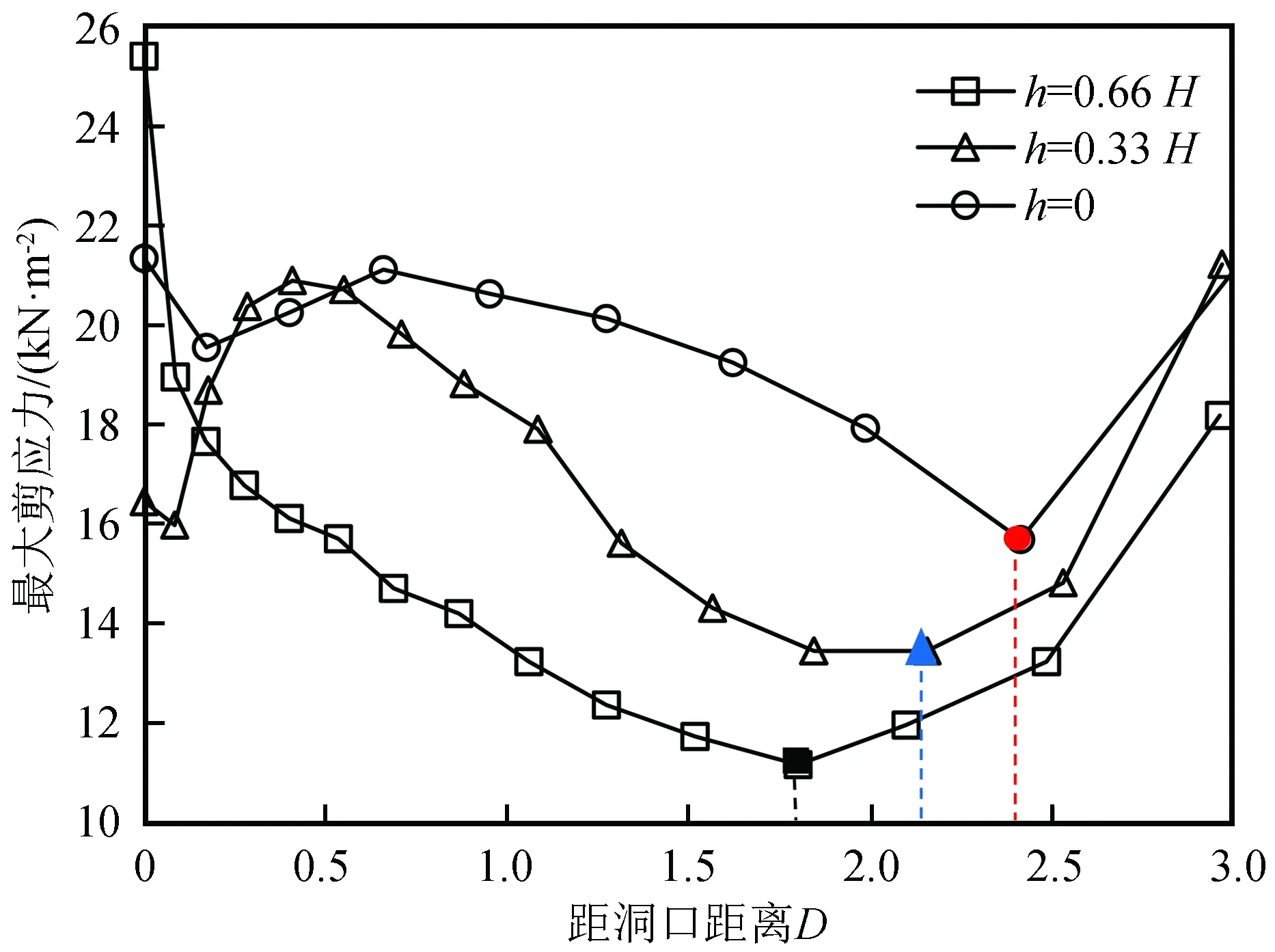
图10 不同入洞高程模型坡面最大剪应力变化曲线Fig.10 Variation curve of maximum shear stress on the slope surface of models with different portal elevation

最大剪应力随洞口距的曲线变化趋势显示放大区的范围为1.8～2.4倍洞径,入洞高程越大,坡面洞口段的动力放大区范围越小。

综上所述,隧道的存在对坡面的水平方向存在动力放大区,放大区的范围与仰坡角度、高度、隧道入洞高程皆有关系,若忽略仰坡角度、高度、隧道入洞高程的变化带来的影响,则洞口周围水平方向动力放大区可取2.1～2.8倍洞径。

坡面高程方向与水平方向的动力放大性存在差异,为探究此差异性的原因,对隧道二衬的最大剪应力分布云图进行了提取。以H=75 m,α=60°,h/H=0.33的模型为例,其二衬最大剪应力云如图11所示。

从图11中可知,隧道在拱腰处的剪应力大于仰拱与拱顶的剪应力,这说明隧道的变形破坏主要是以水平向为主。在坡面的水平方向由于洞口的存在所导致的放大效应会比较明显,而拱顶与仰拱处的剪应力较小。因此对围岩的约束作用较强,反而导致洞口放大效应的明显减小[18]。

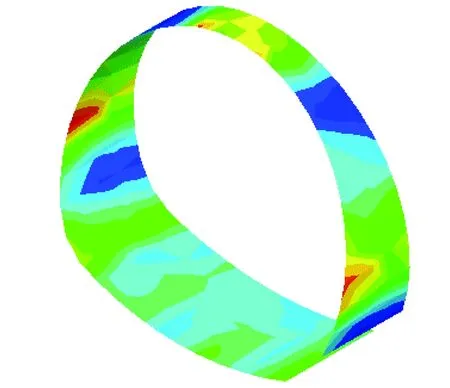
图11 二衬结构最大剪应力云图Fig.11 Cloud chart of maximum shear stress of secondary lining structure

4 隧道进深方向的地震动响应规律分析

隧道进深方向以拱顶的加速度与位移变化规律为代表,探讨隧道洞口段的放大效应,提出抗震加固长度建议值。

图12中“L”为隧道进深长度。分析图12(a)知,隧道在坡底处入洞时,二衬拱顶加速度随着进深的增加呈现“减小-持平-迅速下降-稳定”的变化趋势。有规范和文献[19]建议隧道的抗震设防长度为15～20 m,按照此长度设防则与图12(a)中持平段的终点基本对应,若取持平段的终点长度作为洞口段抗震设防长度,则抗震设防长度可取2.2～3.0倍洞径。若取迅速下降段的终点作为洞口段抗震设防长度,则抗震设防长度可取5.4～6.9倍洞径。总体来说,隧道在坡脚处入洞时洞口段的最小抗震设防长度应为2.2倍洞径;从增加安全储备的角度出发,可设防至6.9倍洞径;取两者的折中点,设计人员可采用4.5倍洞径。图12(b)位移显示随着进深的增加逐渐减小。

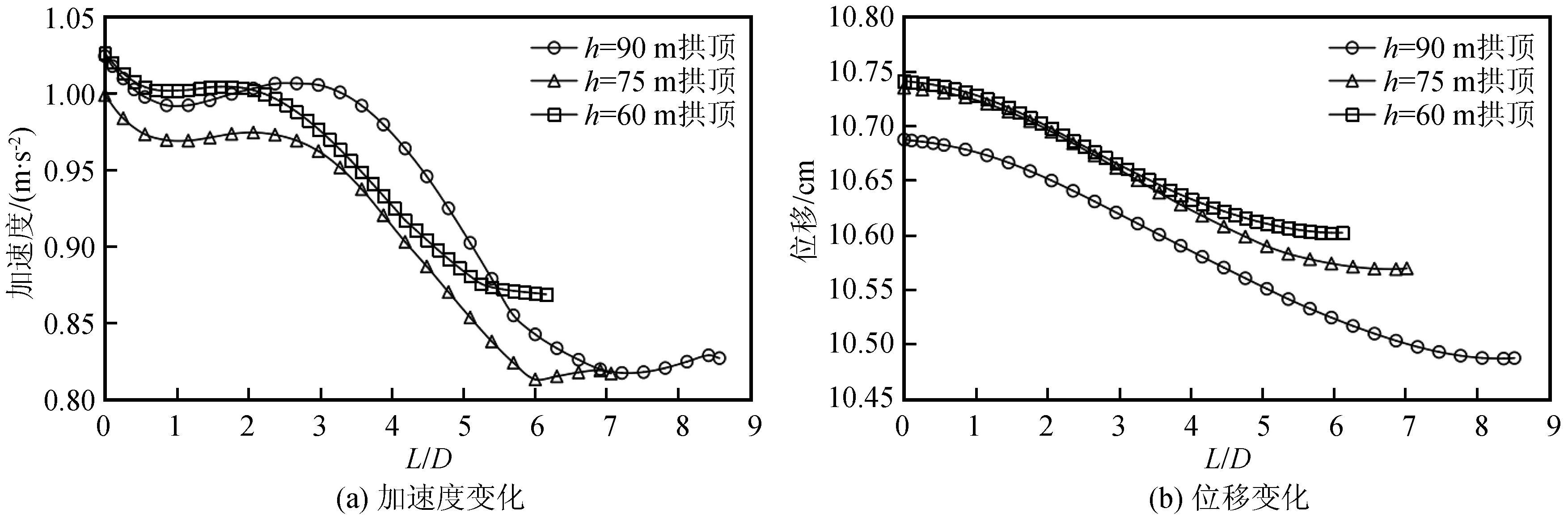
图12 坡底处入洞时隧道进深方向拱顶加速度、位移变化曲线Fig.12 Variation curve of vault acceleration and displacement in the direction of tunnel depth when the portal section is at the bottom of slope

图13为隧道在0.33H高程进洞时二衬的拱顶加速度与位移变化曲线。从图中可知,在坡面处进洞时,加速度的变化规律与在坡底处时不同,呈现随着进深先减小后增大的变化规律,在入口和出口处加速度都有所增加。这是由于隧道入洞高程增加后,隧道的埋深减小,出口处的边界效应显著。取加速度下降段与上升段的交点作为洞口段抗震设防长度,则隧道在0.33倍高程处入洞时的洞口段抗震设防长度可取2.4～4.5倍洞径。

图13 h=0.33H时隧道进深方向拱顶加速度、位移变化曲线Fig.13 Variation curve of vault acceleration and displacement in the tunnel depth direction (h/H=0.33)

图14显示,加速度沿进深变化过程中有三个拐点,1号点对应的位置为0.55D,2号点对应2.95D,3号点对应4.76D。结合坡底处入洞与0.33倍坡高处入洞的洞口段抗震设防长度,0.66倍坡高处入洞时应取2号点2.95倍(≈3倍)洞径作为隧道的抗震设防长度。

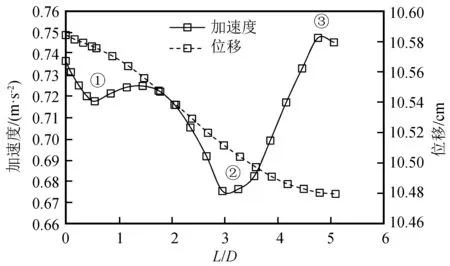
图14 h=0.66H时隧道进深方向拱顶加速度与 位移变化曲线Fig.14 Variation curve of vault acceleration and displacement in the tunnel depth direction (h=0.66H)

综上所述,综合不同仰坡高度、不同仰坡角度、不同进洞高程的模型计算结果,根据二衬沿隧道进深方向的加速度与位移变化规律,将隧道的抗震设防长度总结列于表2。在具体考虑坡度、坡高与进洞高程的影响下,隧道最短抗震设防长度可取3倍洞径。

表2 考虑仰坡高度、仰坡角度与进洞高程影响因素的黄土隧道洞口段抗震设防长度Table 2 Seismic fortification length of portal section of loess tunnel

5 结论

通过对地震作用下不同坡高、不同坡角及不同进洞高程的黄土隧道进行数值模拟,重点分析了坡面垂直向、水平向及隧道沿进深方向的地震动响应规律,得到如下主要结论:

(1)隧道的存在对坡面地震动高程放大效应有重要影响,沿高程方向隧道的存在对周围土体有加固作用,存在一定范围的“自加固”区。通过对不同坡度模型的加速度与位移响应规律分析发现,缓坡易发生坡底处的剪切破坏,而陡坡易发生坡顶的拉裂破坏。随着边坡高度的增大,坡面位移峰值逐渐增大,峰值点的高程却逐渐降低,说明随着高度的增加,边坡的滑动破坏范围逐渐增大。

(2)隧道的变形破坏主要是以水平向为主,隧道的存在对坡面的水平方向存在动力放大作用,放大区的范围与仰坡角度、高度、隧道入洞高程皆有关系。若忽略仰坡角度、高度、隧道入洞高程的变化带来的影响,则洞口周围水平方向动力放大区最小可取2.1倍洞径,从增加安全储备出发则可设防至2.8倍洞径。

(3)综合不同仰坡高度、不同仰坡角度、不同进洞高程的模型,根据二衬沿隧道进深方向的加速度与位移变化规律,建议黄土隧道洞口段抗震设防长度最小取3.0倍洞径,从增加安全储备出发可设防至4.5倍洞径。