基于有限元法的高速列车制动盘散热筋结构优化研究
田露,郝学军
(北京建筑大学 环境与能源工程学院,北京 102600)
0 引言
中国高铁立于全球高铁技术最前沿,并逐步引领全球高铁技术发展。随着高铁技术发展越发成熟,高铁的制动也成为研究热点问题。制动过程中,车辆的动能和势能通过制动盘之间的滑动摩擦转化为热能。有效冷却制动盘,对于确保刹车的安全性和舒适性非常重要[1]。目前,对于制动盘的研究主要是在材料、热-力耦合、温度场等几个方面[2-3]。
当制动盘旋转时,沿着散热筋之间形成的气流通道,热量就可以和外界冷空气进行对流换热。要优化制动盘的散热,散热筋结构十分关键。本文将应用SoildWorks在目前高铁所使用的传统肋片散热筋基础上,优化得到两组新型散热筋制动盘模型,将三维模型进行有限元仿真,得到速度场分析、对流换热系数分布图以及温度场云图。最终期望结合传热学以及流体力学知识改造后的制动盘较之传统散热筋制动盘得到明显的散热优化。
1 优化制动盘模型建立
制动过程中的制动盘是属于旋转机械,将会应用有限元法来进行CFD数值计算。首先运用SoildWorks建立制动盘三维模型。
1.1 传统直肋散热筋
本文选取沿圆周方向均匀分布的直肋散热筋制动盘作为基础模型。如图1所示。

图1 长肋片散热筋制动盘三维模型
主要参数如表1所示。

表1 长肋片散热筋制动盘参数表
1.2 优化散热筋的选择及分布
制动盘旋转时类似于一个离心风机,吸收冷空气使对流换热系数增加,从而增强散热。其对流换热系数主要由表面尺寸、几何参数、流体的物理性质和流动状态来决定。
本文在进行散热筋结构优化设计时,阅读大量文献,对比分析各种散热筋设计。通过分析短肋片斜向分布散热筋和菱形圆周分布散热筋的散热效果,观察短肋片和长肋片的温度分布均匀程度,改造制动盘模型采用分散式长方体形散热筋制动盘和短肋片散热筋制动盘。
在参考《动车组制动盘暂行技术条件规范》下,设计得到两种制动盘模型如图所示。

图2 新型制动盘模型
制动盘所采用的材料为合金锻钢,密度为7.850kg/m3。具体参数如表2所示。

表2 新型制动盘参数表
2 热分析理论基础
流体流动时,需满足质量守恒定律。对于可压缩流体,其瞬态流体质量守恒方程为:
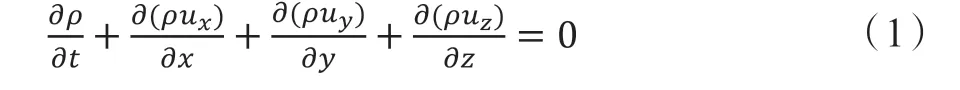
流体流动需满足动量守恒方程也被称作运动方程,即维纳-斯托克斯方程(N-S方程),其微分方程如下所示:
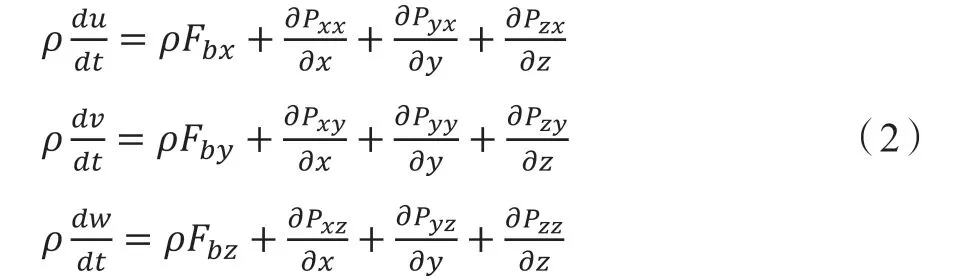
能量守恒方程即为热力学第一定律,其变量是温度,如下所示:
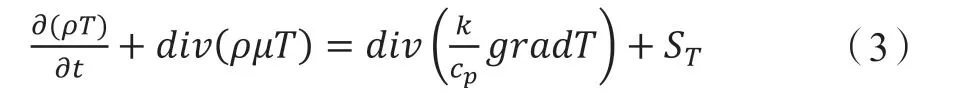
列车制动时将动能通过摩擦面转变为热能。制动盘所吸收的大部分热能,一部分通过热传导传递给散热筋;另一部分通过热对流散至空气中,将其与叶轮机械做类比,进风口吸入空气,出风口流出,空气会带走一部分热量。相关研究表明[4],约有百分之九十的热能会通过对流形式散至空气中。
制动盘所涉及的热传导,可用傅里叶定律描述:

导热微分方程是关于温度场的微分方程,对于不可压缩流体,其导热微分方程可用下式表达:

制动盘的制动过程主要对应非稳态导热。
列车制动时,制动盘盘面会高速旋转,与四周冷空气产生一个相对位移,即存在着对流换热。热对流可根据牛顿冷却公式表示:

制动盘与空气的对流主要为纵掠平板对流换热和横掠管束对流换热。纵掠平板对流换热主要对应于摩擦面内侧及长肋片附近。此时空气流动若为层流,即时,制动盘平均表面传热系数可如下表示:

若空气流动为紊流,即,制动盘的平均表面传热系数如下表示:
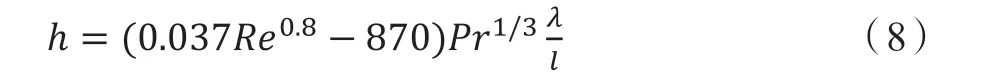
横掠管束对流换热主要对应的是空气与柱状散热筋之间的对流换热形式。此时的平均对流换热系数取决于很多因素,例如流体和壁面的普朗特数,不同散热筋之间的相对间距,以及散热筋排数不同的影响。
3 制动盘流场模拟分析
3.1 建立计算域
列车实际制动过程中,制动盘四周的气流情况是十分复杂的。在制动盘外建立一个可以旋转并相对于制动盘静止的流体区域。此计算域分为旋转域rotation和流场域station。
旋转域模型为底面半径350mm,高180mm的圆柱体。网格划分前,需完成面对象(Part)及体对象(Body)的定义。利用SoildWorks组合删减功能将旋转域和制动盘分别导入模拟软件中。
在制动盘和旋转域之外,需要一个体积更大的流场域。空气流场因为制动盘转动所受到的影响理论上是无穷大的,在保证计算精度且考虑计算机最大计算量后,本文将流场域前外边界长度尺寸取制动盘宽度的2倍;将尾流区长度尺寸定为模型宽度的7.5倍。具体形式如图3所示。
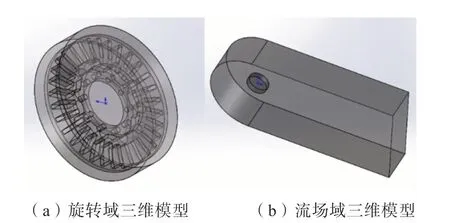
图3 计算域三维模型
3.2 制动盘网格划分
将固体-流体耦合模型导入mesh中,对于散热筋的网格划分需细致,最终的网格数量为二百万到三百万之间。
答案来自第二次世界大战。二战期间,美国海军开发了声呐和回声探测之类的新技术,以寻找德国潜艇。到了和平时期,美国海军发现留下来了一些令人印象深刻的海底地形图。海洋研究继续得到了资助,并形成了第一张详尽的海底地图,由美国地质学家玛丽·萨普(Marie Tharp)和布鲁斯·希森(Bruce Heezen)于20世纪50年代末公开出版。
整体网格尺寸设置为0.08m,最大尺寸设置为0.1m,对于旋转域和流场域来说比较合适。制动盘实体部分进行单独加密,将全局单元尺寸设置为0.005m,网格最大尺寸设置为0.05m。具体的划分情况如下图所示。

图4 制动盘网格划分
3.3 边界条件及求解参数的设定
将入口inlet边界条件设置为速度入口。其初始速度设为列车刚开始紧急减速的300km/h。为使计算结果更合理,选择了距制动盘较远的流场域曲面作为流动入口。将出口outlet边界条件设置为压力出口,压力为一个大气压。本文中的固体-流体耦合模型,即整个计算域被分成了三个域。为使其可进行数据交换,把分别对应制动盘与旋转域,旋转域与流场域交界面的边界条件设置为interface类型,如图5所示。

图5 建立数据可交换设置
将制动盘和旋转域的运动设置为相对运动,转动的角速度和方向是一致的,即设置为Moving Mesh,制动盘与旋转域之间设为Moving Wall。制动盘的速度是300km/h,由式9得出旋转域角速度。旋转方向设置为顺时针。
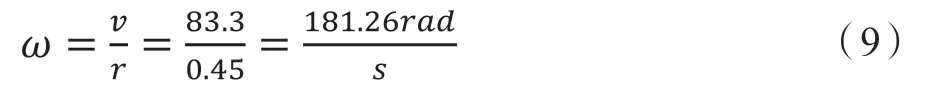
由于本文设置空气流动是不可压缩的,且处于湍流的充分发展段,所以采用针对雷诺数较高的湍流方程Realizable k-模型。Realizable k-方程会提供一个旋转流的修正,对于流体的旋转流动以及流体的流动分离都会产生一个很好的作用效果。在fluent的前期设置阶段,本文采用0.002秒作为时间步长,时间步数则设置为500步。
3.4 模拟结果分析
以下仿真结果的条件为:列车车速300km/h,流场域入口空气速度83m/s,制动盘实体角速度181.26 ,制动盘温度固定500K,流体区域温度设为293K。
3.4.1 速度场分析

图6 制动盘的速度流线图
流线分两种类型,平行规整的直线条对应层流;分布杂乱的曲线对应湍流。空气回流使基础模型通道内存在较大的气旋,气旋处流速较低,对于对流散热有弊处。二、三号模型,气旋更小、更分散,且气旋处空气流速并不很低。主要是散热筋之间通道体积较大,通道数量更多且有许多连通部分。特别是三号模型,流线分布连续且稳定,其气旋呈消失趋势,利于散热。
制动盘周围环境速度场分布云图如图7所示。迎风面速度较小,是由于入口进风和制动盘本身转动的气体流动相抵消。由于制动盘单方向旋转,所以气体速度场的上方和下方并不对称。三个制动盘速度场内的最大流体速度都在220m/s左右,并无太大差别。
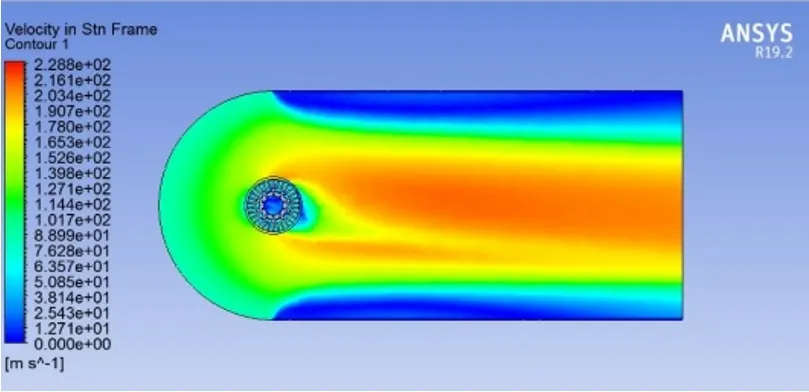
图7 长肋片制动盘内部及环境速度场分布云图
三类制动盘内部通风道速度场分布云图如图8所示。对比分析发现,二、三号模型与空气接触面积更大,对其阻碍更大,所以散热更高效。并且在三号模型迎风面散热筋附近,空气流速为其他模型的1.83倍,约为165m/s,基础模型约为90m/s。
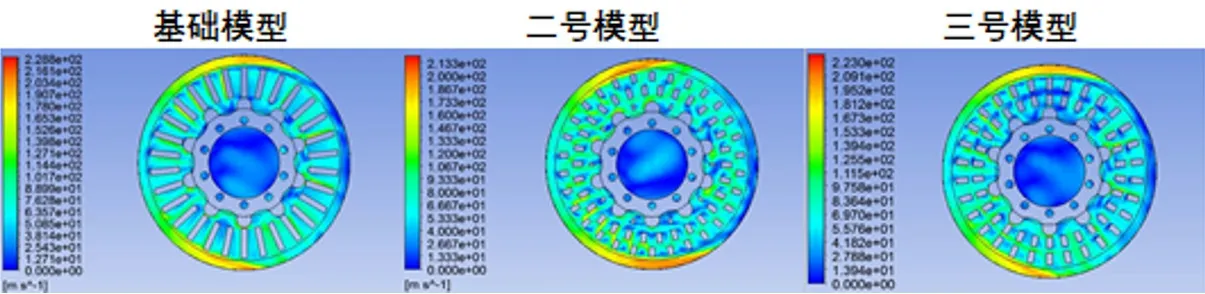
图8 制动盘内部通风道速度场分布云图
3.4.2 对流换热系数分析
对于制动盘散热性好坏起决定性作用的是对流换热系数的大小。从图9上来看,三种类型制动盘的对流换热系数分布差别不大,迎风区域上方系数最大,和速度场云图相呼应。这是由于盘体上下方空气区域无阻碍,气流组织方向较为一致。

图9 制动盘的对流换热系数分布云图
二、三号模型迎风区域上部散热筋的对流换热系数大于基础模型,有利于散热。其中,二号模型的对流换热系数分布更加均匀,整体散热性能比较稳定。
为具体体现制动盘的散热性能优劣,分别取了盘体迎风区域中部、迎风区域中部单个散热筋靠外侧部分、迎风区域上方单个散热筋靠外侧部分、盘体侧面中部这四个位置,来对比其平均对流换热系数,如图10所示。可以得出改造模型部分位置对流换热系数较大,特别是二号模型迎风区域上部散热筋的对流换热系数约为基础模型的1.3倍。

图10 各部分平均对流换热系数柱状图
4 制动盘温度场分析
4.1 假设条件及载荷施加
运用ANSYS中的Transient Thermal 进行温度场模拟。由于列车制动过程较复杂,所以将计算做出简化,采取以下假设[3]:(1)在列车制动时,将整个过程当做匀减速过程。(2)认为制动时的摩擦生热是在两个摩擦面上均等分布的,即温度场会对称于制动盘的中心面。(3)计算初始条件的空气温度为室温,压强为一个标准大气压。
由于要在制动盘摩擦面上施加一个热流密度,于是在每一个摩擦面上都通过面切割的方式,分别划分了一个环状的热流面。这样将会使热流密度有一个均匀并且完整的施加,会更加接近于实际的过程。
在列车制动时,主要施加的载荷有两种,一个是施加对流换热系数,例如,摩擦面内侧可以认为是纵掠平板传热,而对于排列较整齐的散热筋处,其传热形式可以认为是横掠管束对流换热[5]。另一个是热流密度,即摩擦产生的热能,以此种形式施加于摩擦面上[6]。于是根据对流换热系数云图,得到一个制动盘实体对流换热系数范围,然后呈线性施加于制动盘上。
4.2 模拟结果展示
图11即当列车在300km/h的速度下运行时,突然进行紧急制动下三个不同时间点的温度场分布云图。通过模拟验证了制动盘的主要散热依靠于内部的散热筋结构。基础模型和三号模型在散热筋处温度传导快于二号模型。重点表现于图中虚线框处温度值变化。
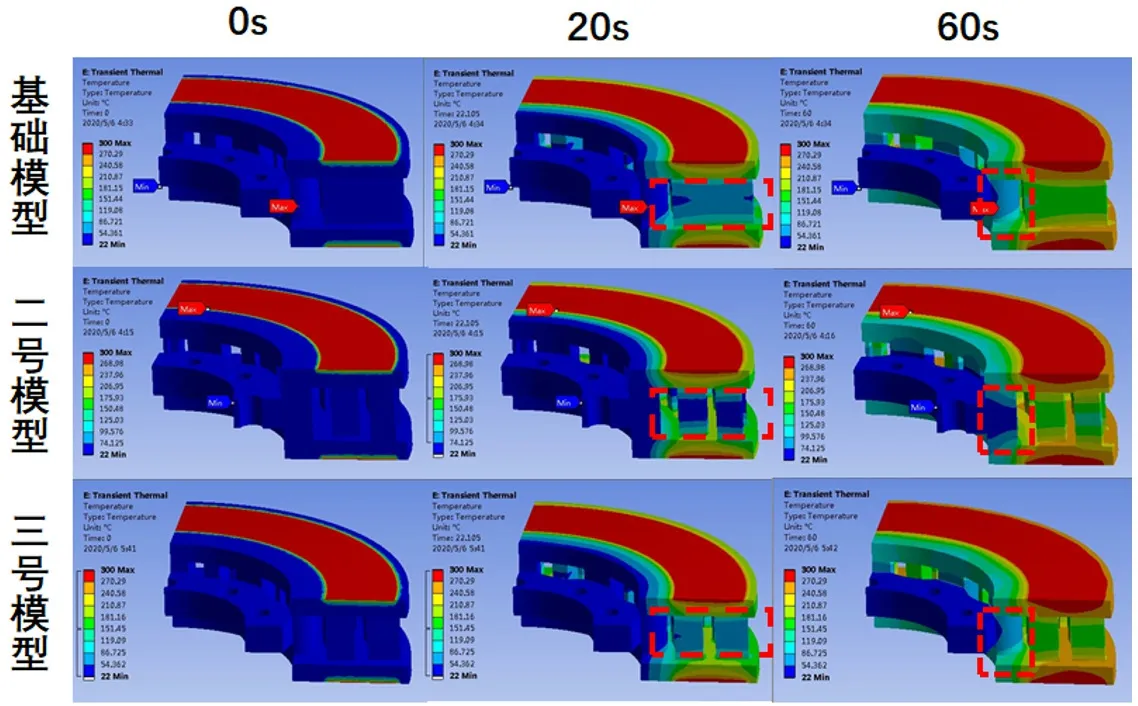
图11 三个时间点的温度场分布云图
5 结语
本文通过模拟分析在制动时三种散热筋制动盘的速度场云图、空气流线图、对流换热系数云图和温度场云图,最终得出主要结论有:(1)二号模型迎风面散热筋的空气流速约为其他模型的1.83倍,其散热性能高于基础模型。(2)基础模型由于气旋,不利于对流散热。改造后模型气流更顺畅,产生气旋体积小。三号模型气旋有流动消散趋势,代表内部通道更适合空气流动。(3)改造后模型迎风区上部散热筋的对流换热系数约为基础模型的1.3倍,且系数分布更均匀,即散热性能更稳定。
在本文的模拟分析中,存在一定局限性。后续建议在如下方面进行研究:(1)通过热应力预测制动盘是否会由于热疲劳产生裂纹以及其使用寿命。(2)各种不同初速度下的制动盘速度场和温度场。

