含变限积分未定式计算中的一点注记
白 斌 杨亚锋 孟利娟
(华北理工大学理学院 河北·唐山 063009)
在高等数学课程的学习中,极限一个是贯穿整个微积分始终的基础概念。极限的计算是课程教学内容中重要的组成部分,针对不同类型的极限形式会有不同的计算方法,所以能够灵活掌握极限的计算方法是学好高等数学的关键。
未定式是极限计算中一种较为常见的类型,包含标准未定式和拓展型未定式两种。标准未定式有:型两种,常用的计算方法有:因式分解或有理化约去零因子、两个重要极限、无穷小等价替换、幂指函数公式、洛必达法则、中值定理以及麦克劳林公式等。拓展性未定式主要有:0∞、∞—∞、00、∞0和1∞型五种,可以通过取倒数、通分、对数变换等方法将拓展型未定式转化为标准未定式。
含变限积分未定式是几种特殊形式未定式极限的典型案例,巧妙地化简积分符号是计算含有变限积分未定式极限的关键。常用的方法主要有:牛顿—莱布尼兹公式、洛必达法则与积分中值定理。其中,利用牛顿—莱布尼兹公式计算变限积分时,有些被积函数的原函数计算比较困难,甚至有些被积函数的原函数不能用初等函数来表示,因此该方法具有一定的局限性。洛必达法则是一种常用的求解未定式极限的方法,对变限积分进行求导可以化简未定式中的积分形式。邢秀侠指出在课堂教学中要特别强调含变限积分的型未定式求极限时应当首选洛必达法则。但是在利用洛必达法则计算未定式时往往需要与其他方法结合使用,如果处理不当会使的计算过程更加繁琐,有时甚至无法求解。积分中值定理可以将未定式中的变限积分转化为积分区间内某一点处的被积函数值与积分区间的乘积,能够巧妙地去掉积分符号。如果积分区间可以与未定式中的其他项相互抵消,将未定式化简为一般式(非未定式),则该方法可以有效简化极限的计算过程;否则,由于不明确的变化速度,无法将两个极限变化过程相互统一,该方法失效。
1 拓展型未定式转化为标准未定式
拓展性未定式主要有:0∞、∞—∞、00、∞0和1∞型五种。其中,0∞型可以通过取倒数,即同除 0或∞转化为型;∞—∞型可以通过通分转化为型;00、∞0和1∞型可以利用对数变换和取倒数运算转化为型。具体转化关系如图1所示。
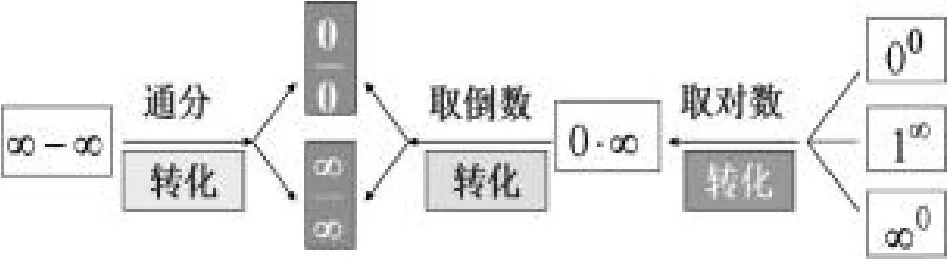
图1:未定式转化关系示意图
2 含变限积分的未定式极限的计算
牛顿—莱布尼兹公式、洛必达法则结合变限积分求导和积分中值定理是常用的三种求解含有变限积分未定式极限的方法。下面通过实例演示三种方法各自的优缺点,主要突出积分中值定理在未定式计算中简捷,且其可行性容易验证的特征。


该实例表明,对于含变限积分的拓展型未定式极限计算,可以先将拓展型未定式转化为标准未定式,然后利用积分中值定理对变限积分进行替换。如果未定式发生退化,针对没有明确表达形式的抽象函数,该方法同样行之有效,此时洛必达法则束手无策。
3 结束语
本文阐述了标准未定式与拓展性未定式之间的转化关系。通过实例对牛顿—莱布尼兹公式、洛必达法则结合变限积分求导以及积分中值定理三种常用的求解含变限积分未定式极限的方法进行对比分析可知,三者特点鲜明,优点明显,缺点同样突出。其中,利用积分中值定理对变限积分进行替换可以有效简化未定式的计算过程,减小计算复杂度,且有效性的判别过程简单、容易验证。所以不要盲目追求洛必达法则,而忽视了积分中值定理的价值。另外,该方法推广到含有多个变限积分或者重变限积分的未定式计算中同样简单、有效。

