水下传感网络中能效感知的相似数据融合算法
刘小强
(1.河南科技大学应用工程学院,河南 三门峡 472000;2.三门峡职业技术学院,河南 三门峡 472000)
0 引言
水下传感网络(Underwater Sensor Networks,USNs)由微型、具有感知和通信能力的传感节点组成。将这些传感节点部署于水下环境,并由它们感知自身周围环境数据,再将所感知的数据传输至信宿或者控制中心。通常,这些传感节点是由电池供电。一旦电池能量用尽,也不便以给节点替换电池或补充能量。因此,如何有效地利用节点能量,进而延长网络寿命,成为USNs 的研究热点[2-3]。
分簇是延长网络寿命的有效技术手段[4-5]。每个簇由一个簇头和多个簇成员构成。簇头收集本簇内成员节点数据;收集后,再传输至信宿。因此,簇头具有融合节点类似操作行为。目前,已有多种形成簇的技术。本文是以已构成簇的WSNs 为研究对象,讨论如何进行数据融合,进而减少数据冗余。
在同一个簇内的传感节点所处的地理位置相距较近。由于处于同一个物理区域,这些节点所感知的数据也存在一定相似,甚至重复。若它们只是简单地将数据传输至簇头,或者簇头对所收集的数据不进行处理,如减少冗余操作,这会增加节点传输的数据量,加大网络负担。
数据压缩是控制数据冗余的有效途径。文献[6]利用数据压缩策略进行融合感测的数据,并提出基于模块对角矩阵的数据融合算法。类似地,文献[7]也提出了基于分布式压缩感知技术。
文献[8]针对UWSNs,提出基于数据融合的构建簇算法,旨在减少UWSNs 内的冗余数据的传输。文献[9-10]将相似函数引入网络,并利用相似函数计算数据间的相似度。尽管这些技术减少了一些相似数据,但信宿所收到的数据仍存在冗余。
为此,提出能效感知的相似数据融合(Energy efficiency-simlarity Aggregation,EESA)算法。EESA算法基于簇化的网络拓扑结构,簇头对簇内成员节点的数据进行压缩,减少数据传输量,进而控制能耗。
1 EESA 算法
1.1 网络模型
考虑簇化的网络结构。即网络内已形成多个簇,每个簇由一个簇头和簇成员构成,如图1 所示。簇头收集簇内成员所传输的数据,并进行数据压缩处理。然后,再由簇头将数据传输至水面上的信宿,然后通过卫星通信将数据传输至数据收集中心。

图1 网络模型
1.2 数据收集模型
考虑周期的数据收集模式。每个节点周期性向簇头传输数据。簇头再传输至信宿[11]。令p 表示周期的时长,每个时长又划分 个时隙,节点在时隙ti内感测数据。令ki表示节点在时隙ti内感测的数据(简称为数据元),且i=1,…,。
1.3 能耗模型
引用文献[1]的能量消耗。水下传感节点以声波作为传输数据的媒介。信号功率随传输距离的增加而衰减。当声波的传输距离为d 时,所衰减的功率为:

其中,f 为声波信号频率。

2 EESA 算法
2.1 数据相似度
在周期p 应用中,每个节点在向簇头传输数据前,先建立数据矢量。令Ri表示节点si的数据矢量,如式(7)所示:

其中,表示在周期p 中总的数据元个数。
为了消除Ri内数据冗余,计算数据元内间的相似度。若两个数据元间的相似度小于预定阈值,则认为它们间数据冗余。具体而言,令ri,j表示数据元ki与kj的相似度,其定义如式(8)所示:

若ri,j<δ,则认为数据元ki与kj间存在冗余。其中,δ 为数据元相似度的阈值。
2.2 数据压缩点
节点si在每个时期p 建立了数据矢量后,并依式(8)计算相似度,若相似度小于δ,则说明存在冗余。在这种情况下,需要对数据矢量进行处理。
EESA 算法引用数据压缩点策略。即将数据矢量Ri转换成代表性的点,并由这些点表述数据矢量Ri。再将这点数据传输至簇头,进而降低数据传输量,也减少了簇头收集数据量。


EESA 算法引用局部融合递归(Local Aggregation Recursive,LAR)算法构建数压点集,其过程如算法1 所示。
节点先计算数据矢量首尾数据元的连线距离,其中定义如式(9)所示:

start、end 分别表示数据矢量第一个数据元索引下标、最后一个数据元索引下标。
然后,再将Ed与阈值td进行比较。如果Ed≤td,则将第一个数据元加入至Pi,如式(10)所示:

节点si先将数据压缩点集Pi和Di传输至自己的簇头。
3 性能分析
3.1 仿真环境
为了更好地分析EESA 算法性能,利用Java 建立仿真平台。在5 000 m×5 000 m 区域内均匀部署180~360 个节点,节点部署的深度为2 000 m。具体的仿真参数如表1 所示。

表1 仿真参数
节点收集海域内海水盐度数据。将这些节点划分2~4 个簇。考虑两个场景:1)场景1:2 个簇,第1个簇有60 个节点;第2 个簇有120 个节点。这2 个簇头分别标记为CH1 和CH2;2)场景2:4 个簇,每个簇的节点为60 个节点。4 个簇头分别标记为CH1、CH2、CH3 和CH4。每个节点收集数据,再传输至自己的簇头。
同时,选择基于优适相似度的(Well-suited Similarity Functions,WSF)[10]数据融合算法作为参照,并分析它们的性能。在实验中,考虑不同的 尺寸和阈值td对性能影响。
3.2 数据分析
3.2.1 实验1
本次实验分析在场景1 环境下,节点发给簇头的数据比例(简称节点传簇头数据比),如图2 所示。 分别取值128、256、512 和1024。阈值δ 从0.001、0.005、0.01 和0.025 变化。

图2 节点传簇头数据比(场景1)
从图2 可知,EESA 算法有效地降低了节点传输至簇头的数据比。最大的节点传簇头数据比也不过40%,最低为3%。这说明:利用EESA 算法能够有效压缩数据,极大地降低了数据冗余量。此外,从图2可知,δ 或 的增加,降低了节点传簇头数据比。原因在于:随着δ 或 的增加,认定数据冗余的条件变得苛刻,因此,压缩数据的力度越大,使节点向簇头传输的数据量越小。
3.2.2 实验2
本次实验分析在场景1 环境下,信宿所收到来自CH1 和CH2 的数据比例,并与WSF 算法进行比较,如图3 所示,其中阈值δ 取0.005。

图3 簇头向信宿传输的数据比(场景1)
从图3 可知,EESA 算法中每个簇头(CH1 和CH2)向信宿传输的数据比远低于WSF 算法。在 变化期间,EESA 算法的性能均优于WSF 算法,传输至信宿的数据比低于4%。可是WSF 算法的簇头向信宿传输的比例达到50%。此外,CH1 和CH2 向信宿传输的数据比例相近。
3.2.3 实验3
本次实验分析EESA 算法执行时间,并与WSF算法进行比较,其中阈值δ 取0.005。图4 显示了场景1 环境下,EESA 算法和WSF 算法的两个簇头(CH1 和CH2)的执行时间。

图4 2 个簇头的运行时间(场景1)
从图4 可知,相比于WSF 算法,EESA 算法有效地控制了算法的运行时间。例如,在=1 024 时,EESA 算法的执行时间约50 ms,而WSF 算法的执行时间达到150 ms。这归功于EESA 算法利用欧式距离对数据压缩,减少了数据处理量,极大地缩短了运行时间。
图5 给出场景2 环境下EESA 算法和WSF 算法的4 个簇头的平均运行时间。从图可知,平均运行时间随数据元个数的增加而呈上涨趋势。原因在于:数据元个数越多,簇头需要处理的数据量就越大,必然增加了运行时间。
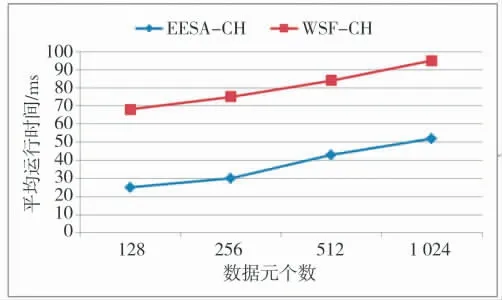
图5 4 个簇头的平均运行时间(场景2)
此外,相比于场景1,场景2 环境中簇内的节点数减少,运行时间下降,并且WSF 算法与EESA 算法的运行时间差距缩小。
3.2.4 实验4
引用文献[4]的能耗模型,本次实验分析EESA算法的节点能耗。

图6 EESA 算法中节点的平均能耗(场景一)
表2 给出EESA 算法与WSF 算法的节点平均能耗,其中,EESA 算法的数据来自取δ=0.001 情况。从表2 可知,相比于WSF 算法,EESA 算法有效地减少了节点能耗。并且随着 的增加,EESA 算法在能耗方面的优势越大。原因在于:EESA 算法通过压缩冗余数据,减少了节点所传输的数据量,进而减少了节点能耗。

表2 EESA 算法与WSF 算法的节点平均能耗
3.2.5 实验5
本次实验分析数据压缩误差。压缩误差体现了数据经压缩解压后数据的失真度。压缩误差越大,信息失真度越大,信息丢失越严重。压缩误差的定义如式(12)所示:

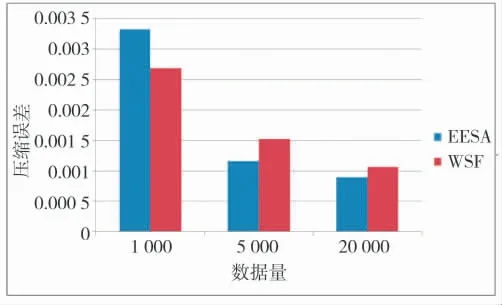
图7 压缩误差
4 结论
本文提出能效感知的相似数据融合算法EESA。EESA 算法对节点传输的数据进行压缩,减少数据冗余量。每个节点将收集的数据进行压缩,再传输至簇头,避免了冗余数据在网络内的传输。相比于WSF 算法,EESA 算法控制网络数量流量,减少了能耗。

