波形钢板组合墙对拉螺栓受力机理及设计方法

王宇伟，郭彦林，刘王恢，朱靖申

(1 浙江中南建设集团钢结构有限公司，杭州 310052；2 清华大学土木工程系，北京 100084)

0 引言

建筑工程上应用的剪力墙主要分为钢板剪力墙和混凝土剪力墙[1]。钢板剪力墙又可分为非加劲钢板墙、加劲钢板墙、防屈曲钢板墙、波形钢板墙以及钢板-混凝土组合墙(简称钢板组合墙)。钢板组合墙形式多种多样，又可分为双钢板内嵌混凝土组合墙和混凝土外包钢板组合墙。双钢板内嵌混凝土组合墙采用外侧钢板约束混凝土，由于能发挥钢板与混凝土材料二者各自的优势，具有良好的受力性能。波形钢板-混凝土组合墙(CDSCW)[1，2]是一种较新的结构形式，其采用两块波形钢板内筑混凝土且通过对拉螺栓连接而成，具有更优越的受力性能。清华大学郭彦林课题组对波形钢板组合墙进行了较系统和深入的研究[1-12]，其研究成果已经反映到《波形钢板组合结构技术规程》(T/CECS 624—2019)[12]中。

波形钢板组合墙依据结构的平面布置，可分为一字形、L形和T形等多种截面形式，其结构设计理论主要包括截面承载力、整体稳定承载力和墙肢稳定承载力计算等。在波形钢板组合墙组成中，除了外侧波形钢板和内筑混凝土外，其承力单元还有连接它们的对拉螺栓。对拉螺栓将两块波形钢板连接，起到对波形钢板向外侧挠曲变形的牵制作用，加上内筑混凝土对波形钢板向内挠曲变形的约束作用，使波形钢板屈曲荷载大大提高。然而，波形钢板墙在压弯荷载作用下，由于混凝土的泊松效应在面外方向产生膨胀，其在极限状态下螺栓会承担比较大的拉力，可能发生螺栓的破坏。为避免发生螺栓破坏，有必要对螺栓受力机理进行研究，并得到螺栓拉力设计计算公式，作为波形钢板墙承载力设计方法的一部分。

文献[13]介绍了波形钢板组合墙对拉螺栓拉力测试试验，主要介绍了在浇筑混凝土过程中螺栓拉力的变化。试验结果表明，在混凝土浇筑后的120min内，随着混凝土逐步凝固，螺栓拉力迅速衰退并稳定在非常小的水平。本文主要研究波形钢板组合墙在轴向压力作用下螺栓的受力机理，进而提出螺栓拉力的计算方法，并保证螺栓破坏不先于波形钢板墙的破坏。

1 螺栓拉力理论推导

首先建立螺栓拉力推导的理论模型。模型中只考虑波形钢板组合墙的波形部分，并假设波形部分无限宽(图1(a))。因此在波形部分混凝土受压后，其无法沿着平面内方向膨胀，而只能向波形钢板组合墙平面外侧向膨胀，且其侧向膨胀和波形钢板的平面外方向移动一致。对于波形钢板而言，其在波形钢板组合墙平面外方向受到波形部分混凝土对其施加的侧向接触力和对拉螺栓被动产生的拉力，这两个力大小相等、方向相反。该侧向接触力是不均匀的，且其具体分布和波形钢板厚度、竖向螺栓间距等参数均有联系，受力较为复杂。为简化计算，不妨先考虑双层平钢板内嵌混凝土组合墙的情况，这样混凝土对钢板的膨胀力均匀分布，且混凝土和螺栓在平面外方向上也发生均匀变形。

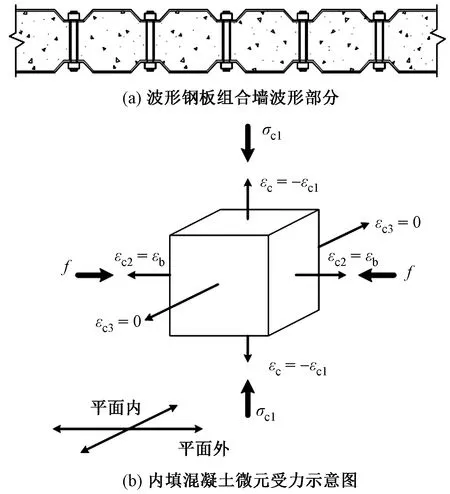
图1 波形钢板组合墙波形部分及内填混凝土微元

图1(b)为内填混凝土微元所受到的力，其竖向应变记为εc1，应力记为σc1。若竖向压力在该混凝土微元上产生的压应变为εc，则有式(1)成立。水平方向上，平面外方向应变记为εc2，应力记为σc2，平面内方向应变记为εc3。根据上文波形部分无限宽的假设得到式(2)。若记螺栓的拉应变为εb，根据螺栓和混凝土在平面外方向上的变形协调关系，有式(3)成立。混凝土微元在平面外方向受到均匀膨胀力，记为f，该力应和混凝土微元在平面外方向上受到的应力大小相等，如式(4)所示。若记螺栓截面面积为Ab，螺栓弹性模量为Eb，单个螺栓所约束的波形钢板面积为Ai，Nb为单个螺栓拉力根据波形钢板在平面外方向上的受力平衡，有式(5)成立。单个螺栓所约束的波形钢板面积由式(6)计算，式中d1为竖向螺栓间距，d2为横向螺栓间距。

εc=-εc1

(1)

εc3=0

(2)

εc2=εb

(3)

f=-σc2

(4)

Nb=AbεbEb=Aif

(5)

Ai=d1d2

(6)

根据以上关系式并结合经典弹性力学理论[14]，即可得到螺栓拉应变εb和混凝土微元压应变εc之间的关系式(7)，式中Ec，νc分别为混凝土的弹性模量和泊松比。由于螺栓拉应变直接决定了螺栓拉力，因此根据该式即可确定螺栓拉力设计公式的基本形式。由式(7)可见，螺栓截面面积Ab和单个螺栓所约束的波形钢板面积Ai是影响螺栓拉力的重要参数，其中Ai又由竖向螺栓间距d1决定。同时考虑到该模型做了平钢板-混凝土组合墙的假设，而实际上由于波形钢板的影响，膨胀力并非均匀分布，其和波形钢板-混凝土之间的相对刚度分布有关，即会受到波形钢板厚度ts的影响，因此波形钢板厚度ts也是影响螺栓拉力的重要参数。为了便于根据有限元模型确定螺栓拉力计算公式中的参数，同时考虑模型简化带来的影响，将式(7)改写为式(8)。根据以上分析，其中系数αb，βb应和Ab，d1，ts相关。

(7)

(8)

2 试验研究与有限元模拟

2.1 试验设计

波形钢板组合墙试验试件高度为1.5m，螺栓布置形式为正交布置，竖向间距为750mm，水平间距为200mm(图2(a))。组合墙试件的截面形式如图2(b)，2(c)所示，其中波形部分宽度为1.07m，墙厚度为168mm，波形钢板厚度为4mm，竖向边缘构件钢管混凝土宽度为160mm，厚度为160mm，管壁厚度为5mm。试验试件的混凝土设计强度等级为C40，钢材设计强度等级为Q345B。

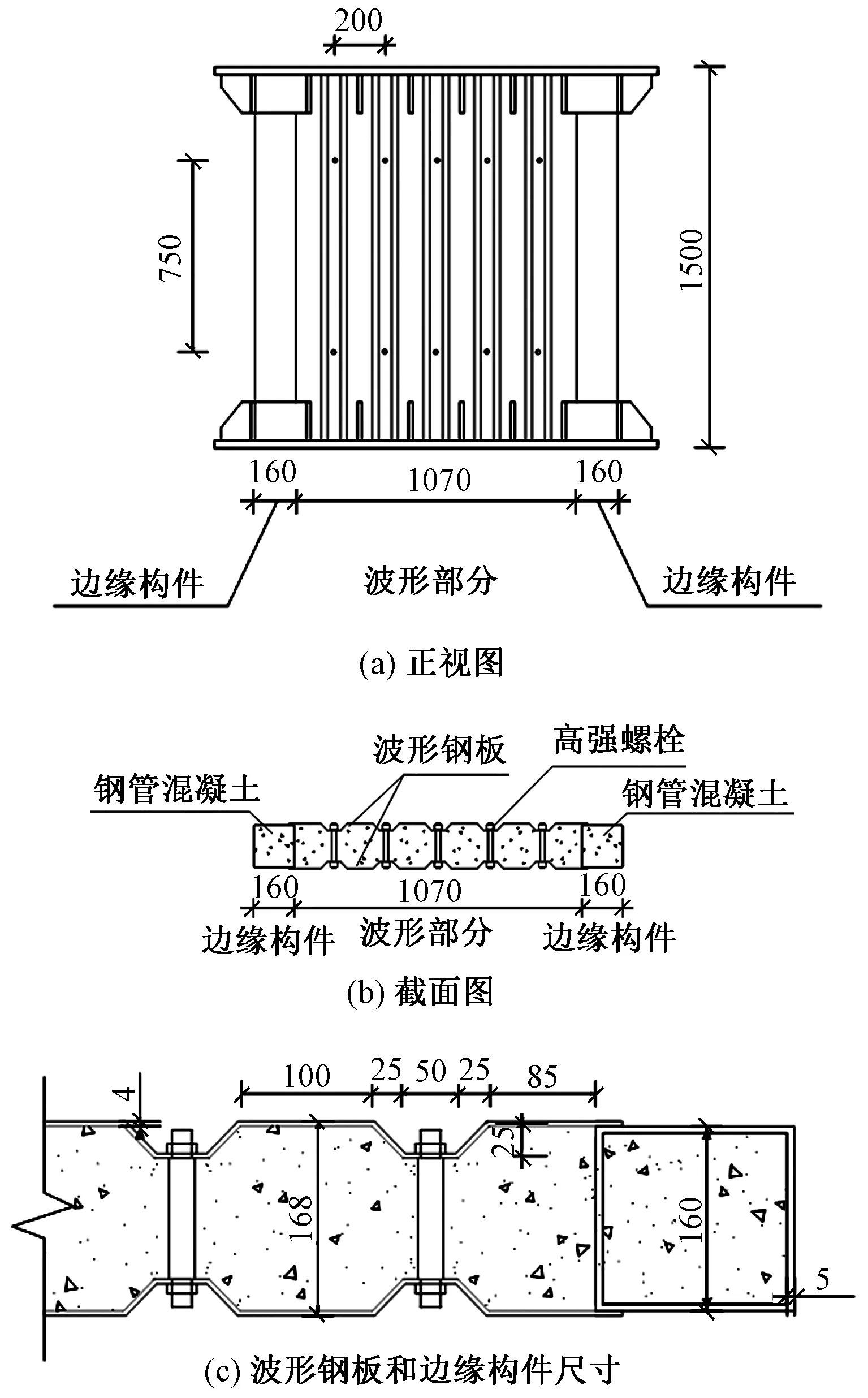
图2 试验试件示意图/mm

试验加载装置立面如图3所示。试件上下端分别和刚性加载梁与基础梁用高强螺栓固接。加载梁上表面设置千斤顶，以便对试件施加竖向荷载；基础梁通过锚栓固定在试验台座上，南北方向通过限位梁和抗剪件嵌固在两排受剪孔之间。尽管千斤顶的加载板上方设置有球铰，但由于试件高度较小，且球铰上的摩擦系数较大，足以确保试件在加载中其整体失稳破坏不会先于强度破坏。

图3 试验试件的试验加载装置示意图

根据材性试验得到混凝土轴心抗压强度实测值为36.9MPa，钢材屈服强度为476MPa，极限强度为556MPa。关于加载制度，在试验开始之前根据材性试验得到的混凝土和钢材实测强度，预估试件的预测屈服荷载Ny。加载过程中，在荷载达到预测屈服荷载的一半之前，采用力控制法加载；在荷载达到预测屈服荷载的一半之后，采用位移控制法加载，并直到试件破坏，试验结束。

2.2 试验现象

波形钢板组合墙试验试件仅承受竖向压力直到破坏。达到承载力极限状态时，位于试件西侧的、和上排螺栓等高的波形钢板波峰处发生局部屈曲，同时两侧边缘构件钢管顶部发生局部屈曲，破坏时的变形如图4所示。

图4 试验试件破坏时变形情况

2.3 有限元模拟

图5为利用ABAQUS软件建立的精细化CDSCW有限元模型，该模型能够反映螺栓对波形钢板的约束作用。模型各项参数及边界条件均与试验试件保持一致。其中，波形钢板采用壳单元模拟，采用理想弹塑性本构关系；波形部分和边缘构件的内填混凝土采用实体单元模拟，采用塑性损伤模型；混凝土波形钢板上根据实际螺栓孔大小进行开孔，螺栓采用杆单元进行模拟，采用理想弹性本构关系，且杆单元两端和螺栓孔周围钢板柔性耦合，即螺栓对该处钢板有一定的约束作用，与实际情况更为相符。柔性耦合通过ABAQUS中的Structural Distributing功能实现，其中Weight Method表示柔性约束分布模式，参数Influence Radius表示螺栓对钢板的约束程度，该值越大则约束作用越强。通过调节该值即可得到不同的组合墙竖向荷载-螺栓拉应变相关曲线，并与试验曲线进行对比。

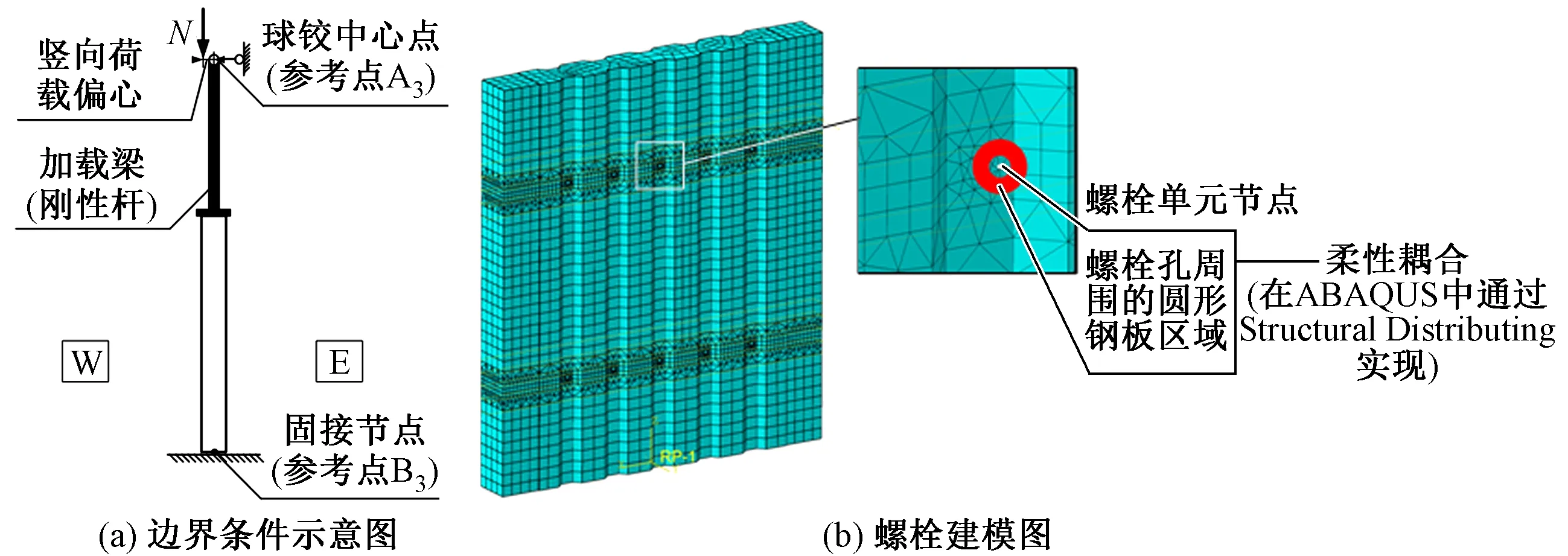
图5 有限元模型

经过一系列试算，最终确定当Weight Method取Cubic，Influence Raidus取0.022时组合墙竖向荷载-螺栓拉应变相关曲线与试验曲线吻合度最高。图6为有限元模型的破坏模式，与图4试验试件的破坏模式相比，二者破坏模式一致，均在和上排螺栓等高的波形钢板波峰处发生局部屈曲。图7为有限元模型和试验试件的竖向荷载-螺栓拉应变相关曲线对比图，可见在图中A/a点以前的加载阶段，有限元模型对螺栓拉力的模拟相当准确，而在A/a点以后的加载阶段，波形钢板开始发生局部屈曲，混凝土接近极限受压状态使得其泊松比迅速增大，这些强非线性特征使螺栓拉力在组合墙的极限状态附近出现了较为复杂的变化过程。直到极限状态后螺栓拉力的发展趋势才重新稳定。此时由于波形钢板的局部屈曲对螺栓产生了强烈的平面外方向的牵扯作用，因此螺栓拉力迅速增大。在实际设计中，只需保证波形钢板组合墙到达极限状态时螺栓不发生受拉屈服即可。由于有限元模型对极限状态下的螺栓拉应变模拟并不理想，而对A/a点处的螺栓拉应变模拟较为准确，因此可用于寻找极限状态下螺栓拉应变和A/a点螺栓拉应变的关系。图中B点表示试验试件的极限状态，可见此时的螺栓拉应变不大于A/a点的2倍。出于保守考虑，在计算得到A/a点螺栓拉应变后乘以2，作为极限状态下的螺栓拉应变。

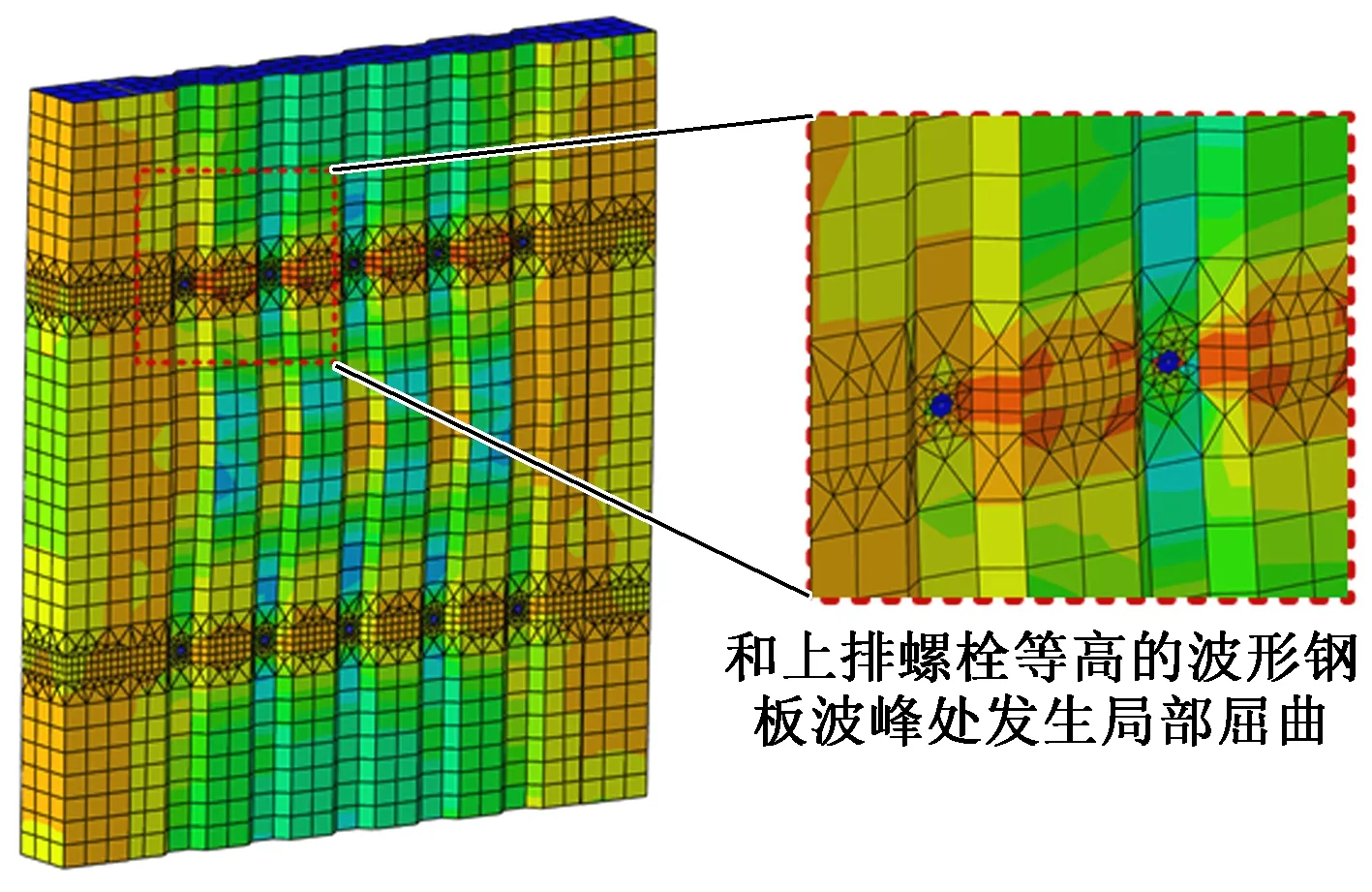
图6 有限元模型的典型破坏模式

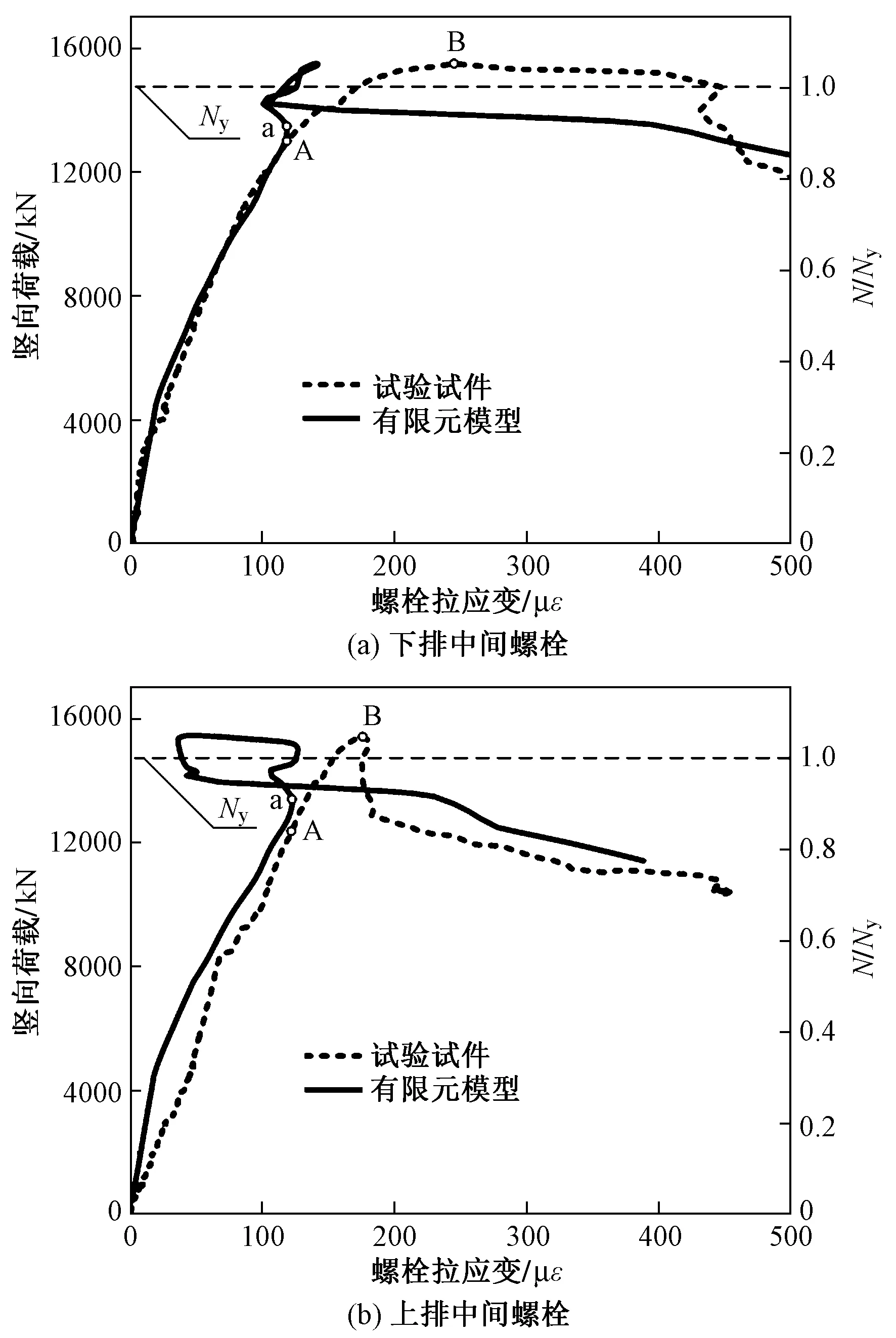
图7 有限元模型和试验试件的竖向荷载-螺栓拉应变相关曲线对比

3 参数分析

以上述有限元模型为基础进行参数分析。根据第1节的理论推导，螺栓截面面积Ab、竖向螺栓间距d1和波形钢板厚度ts将作为重要参数。

3.1 螺栓截面面积Ab的影响

如图8(a)所示为混凝土竖向压应变和螺栓平均拉应变的比值εc/εb和螺栓截面面积Ab的关系。由图可见，随着螺栓截面面积Ab的增大，比值εc/εb迅速增大，且两者之间呈现出线性关系，这一规律和式(8)一致。可以推测，参数αb，βb应和Ab无关。从定性角度判断，螺栓截面面积的增大使得螺栓只需要更小的拉应变，即可提供足够对波形钢板的约束作用。

3.2 波形钢板厚度ts的影响

如图8(b)所示为混凝土竖向压应变和螺栓平均拉应变的比值εc/εb和波形钢板厚度ts的关系。由图可见，随着波形钢板厚度ts的增大，比值εc/εb迅速减小。从定性角度分析，波形钢板厚度ts的增大意味着其刚度的增大，这使得混凝土的侧向膨胀力更直接地带动波形钢板向平面外方向移动，因此螺栓受到更大的拉力。由于式(8)中并没有直接体现波形钢板厚度ts，因此可以推测参数αb，βb应和ts呈负相关关系。

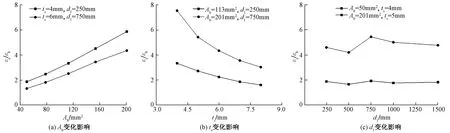
图8 不同参数下的εc/εb曲线

3.3 竖向螺栓间距d1的影响

如图8(c)所示为混凝土竖向压应变和螺栓平均拉应变的比值εc/εb和竖向螺栓间距d1的关系。由图可见，两者之间并无明显的相关性。从定性角度分析，一方面，竖向螺栓间距d1的增大使得每个螺栓所需要约束的钢板面积增大了，这将导致螺栓拉力的增大；另一方面，竖向螺栓间距d1的增大又削弱了波形钢板-对拉螺栓体系的平面外刚度，这又在一定程度上削弱了混凝土侧向膨胀力向波形钢板的传递，从而减小了螺栓拉力。两种效应互相抵消，导致了εc/εb和d1并无显著相关性。由于式(8)中的Ai和d1直接相关，而Ai和εc/εb在式(8)中呈现出负相关关系，因此可以推断参数αb，βb应和d1呈正相关关系，以抵消Ai对εc/εb的影响。

4 螺栓拉力设计公式

根据第3节的参数分析，αb，βb和d1呈正相关关系，和ts呈负相关关系，因此假设参数αb，βb均和d1/ts相关。在螺栓截面面积Ab、竖向螺栓间距d1和波形钢板厚度ts的参数范围内进行数值计算并拟合后，即可得到式(9)、式(10)。图9为εc/εb的公式值和有限元值对比，可见式(9)、式(10)的精度良好，只有部分算例的相对误差略大于10%。再根据式(5)即可得到螺栓拉力计算公式(11)，其中ηb为极限状态螺栓拉应力发展系数，根据第2节的分析取2.0；εc为波形钢板发生局部屈曲的临界混凝土压应变，偏于安全取为0.002；ftb为螺栓材料的抗拉强度设计值。式(11)也可以改写为每个对拉螺栓在所约束波形钢板面积内所能承担的平均膨胀力fa的形式，如式(12)所示。

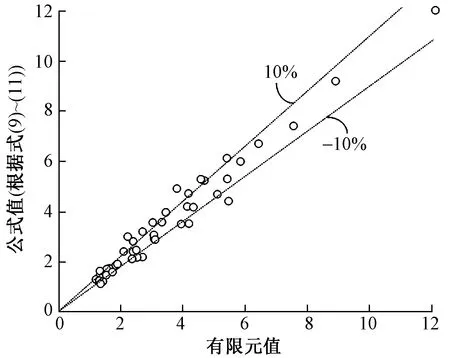
图9 εc/εb的公式值(根据式(9)～(11))和有限元值对比

(9)

(10)

(11)

(12)

5 结论

本文通过理论推导、试验研究和参数分析得到波形钢板组合墙对拉螺栓拉力的设计计算公式。主要结论如下：

(1)根据理论推导，得到螺栓拉应力的重要影响参数有：螺栓截面面积Ab、波形钢板厚度ts、竖向螺栓间距d1，并分析了它们对于螺栓拉应力的影响。

(2)得到与试验结果吻合度很高的有限元模型，利用该有限元模型进行了参数分析。

(3)通过数值算例计算结果，拟合得到波形钢板组合墙对拉螺栓设计计算公式，公式值与有限元值吻合度较高，公式有很好的精度。