轨道交通大功率模块化不间断供电电源可靠性和经济性分析
许铭林,陈艳峰,廖 慧,张 波,丘东元
(1.华南理工大学电力学院,广州 510640;2.广州科技贸易职业学院智能制造学院,广州 511442)
随着轨道交通跨入“高速时代”,通信、信号、综合监控、办公自动化等弱电系统在轨道交通中的应用范围不断扩大。这些系统负责轨道交通的运营指挥、设备与环境监控、信息传递和乘客引导等功能,对供电电源的质量和可靠性有着极高的要求。因此,为保证轨道交通系统的正常运行,需配置大功率、高可靠的不间断供电电源UPS(uninterruptible power system)作为电力保障。在UPS 的配置标准上,我国于2009 年开始实施的《电子信息机房设计规范》对机房的不间断电源冗余配置做出了技术要求[1];同时,提高UPS 的可靠性会相应增加其经济成本。因此,在轨道交通信号系统供电电源的实际设计中,应在满足可靠性需求的前提下,寻找成本最低的UPS 配置方案。
针对信号电源系统UPS 配置方案的可靠性分析与经济性分析,已有许多文献开展了研究。文献[2]介绍了数种调度集中信号电源系统的配置方法;文献[3]对这些配置方案进行了进一步对比分析,并根据不同的负载需求提出对应的建议配置方案;文献[4]计算了不同方案的UPS 系统的可靠性指标,从定量的角度对比了各方案的异同;文献[5]研究了不同UPS 配置方案的可靠性与经济性综合对比,但其经济成本计算方法过于简化;文献[6]对UPS 的可靠性与经济性做了综合评估,提出了配置UPS冗余方案的计算方法,但其分析限定于传统的单模块UPS;文献[7]进一步完善UPS 可靠性模型,提出多种UPS 配置方案的可靠性框图模型,并对比不同模型的异同;文献[8]采用GO-贝叶斯方法,介绍了一种计算UPS 系统可靠性的方法,其理论结果得到了蒙特-卡罗法仿真验证;文献[9]进一步对UPS系统中各模块可靠性参数的敏感性进行了分析,由此可确定UPS 系统中可靠性较薄弱的环节,具有较大的应用价值。
随着UPS 技术的发展,模块化UPS 逐渐取代传统的单模块UPS,成为UPS 配置的主流。但模块化UPS 中采用多个子模块共同承担负载并配置冗余,其内部形成k/n 表决系统,工作过程更为复杂。针对模块化UPS,文献[13-15]分别从接线方式、电池检测、系统架构3 个方面分析了提高模块化UPS稳定性的方案,文献[16]分析了大功率模块化UPS内部温度设计与可靠性的关系。
本文针对模块化UPS 的结构特点和运行方式,基于马尔可夫理论建立其可靠性框图模型,求解可靠性指标,并运用蒙特-卡罗法验证所得结果的有效性。最后本文对UPS 运行过程中产生的各种成本进行了归纳,提出了一种计及时间成本和运行损耗的UPS 经济性评估方法。
1 可靠性评价指标与典型分析方法
1.1 可靠性评价指标
UPS 的负载端可以视作一个小型的配电网系统,其可靠性分析需要建立其中每个元件的可靠性模型,并分析其可靠性指标[6]。对于系统中的单个元件,其可靠性指标主要通过可靠性模型和数据统计的方法获取。本文重点关注以下4 个可靠性指标。
(1)故障率λ。故障率是最基本的可靠性指标之一,指元件无故障运行时间TF后,在单位暴露时间Δt 内运行发生故障、不能执行规定功能的概率。其定义为
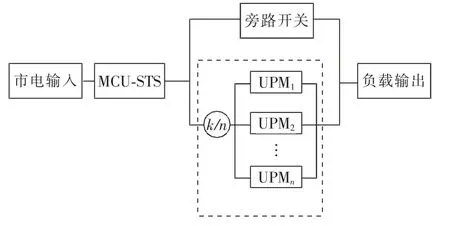
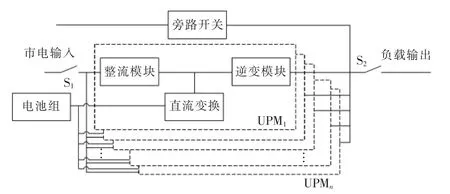
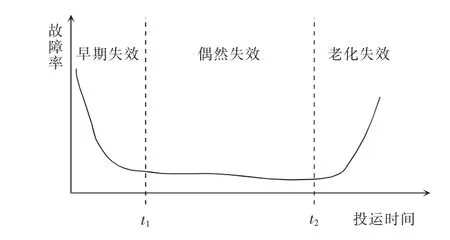
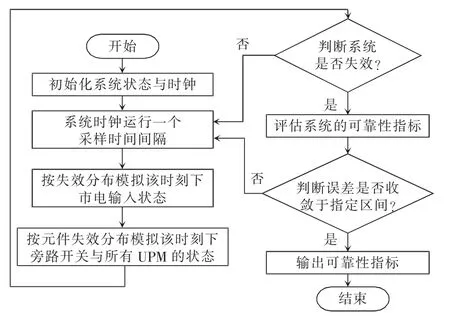
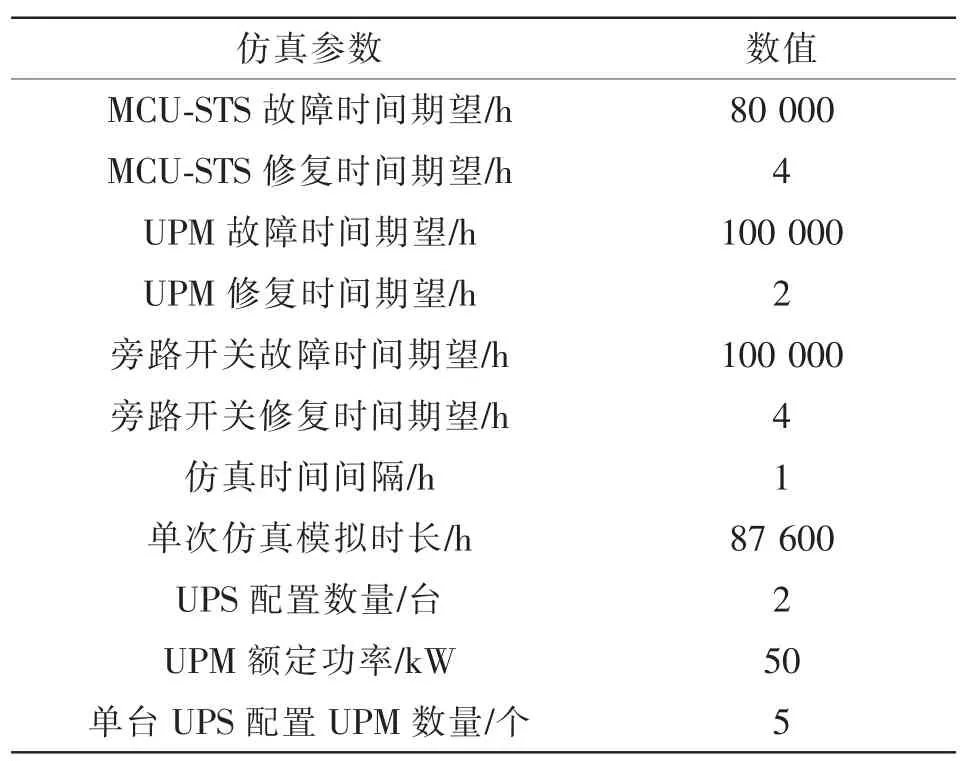
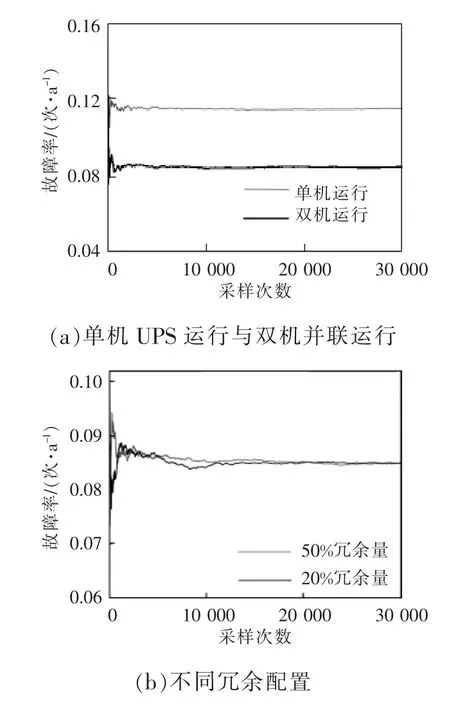
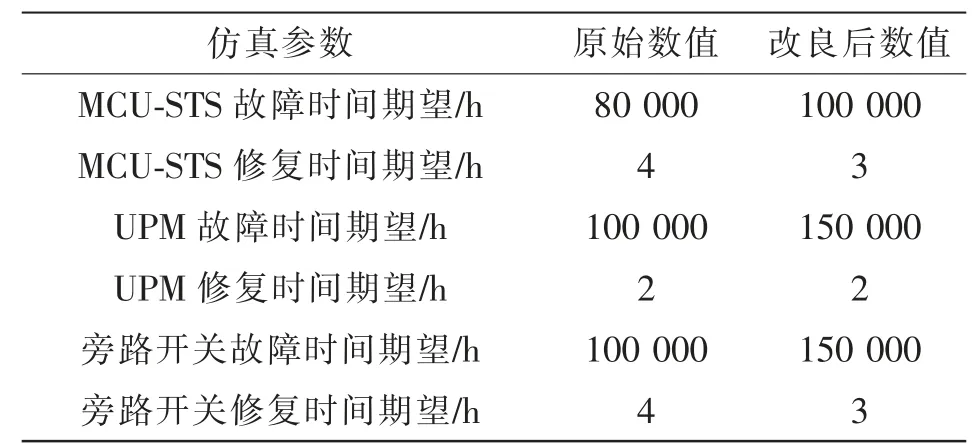
式中:tTTF为设备无故障运行的时间长度;P(TF (2)修复率μ。修复率是指元件发生故障并经过时间TR后,在Δt 内修复故障,并恢复至正常原有功能的概率。与故障率类似,其定义为 式中:tTTR为设备从发生故障到完成修复至正常原有功能的时间长度;P(TR (3)平均无故障时间TMTTF与平均修复时间TMTTR。二者分别指可修复元件在长时间运行中平均每次正常运行持续的时间与平均每次发生故障的持续时间。实际可靠性评估中,故障率与修复率往往难以通过定义准确计算,因此常用平均无故障时间与平均修复时间进行近似计算,即 (4)可用度a 与不可用度u。二者分别指元件某一时刻处于正常工作状态的稳态概率与处于故障状态的稳态概率。可用度与不可用度可以通过故障率与修复率计算求得,即 对于随机变量X(t),其所有取值的集合称为状态空间,记作E。若对于任意的时间序列t1 对一个马尔可夫过程,当某个时刻tn的变量状态X(tn)已确定,则其未来的变量状态与历史状态无关,只与tn时刻的变量状态有关。在可靠性分析中,常假设系统的运行属于马尔可夫过程,以简化运算量与求解难度[12]。 对于具有离散时间参数和有限状态的马尔可夫过程,可以列写其马尔可夫链,其模型如图1 所示。 图1 马尔可夫链状态转移过程模型Fig.1 States transfer process model of Markov chain 图1 展示了一个三状态系统每经过固定的时间t 后状态发生转移的过程。假设系统运行在状态1,则经过时间t 后,系统将以p12的概率转移到状态2,也可能以1-p12的概率继续运行在状态1。将状态转移的概率表示为矩阵形式,则得 矩阵Q 称为图1 的马尔可夫链的状态转移矩阵,表征随机过程的状态转移概率,矩阵中的元素pij表示系统经过时间t 后,从状态i 转移到状态j的概率。在tn时刻将系统各个状态的概率表示为列向量Pn,则可计算得到tn+1时刻的概率分布为 式(9)可推广至任意时刻tn+i,即 式(10)表明,当一个马尔可夫过程某一时刻tn的概率分布已确定时,则其后任意时刻的概率分布均可通过状态转移矩阵运算求得。 进而,可以通过状态空间法求解其稳态可靠性指标。该方法步骤为:确定系统状态空间全集E,根据状态间的转移概率列写状态转移矩阵。此后,通过马尔可夫极限定理即可求得该系统的稳态概率分布。 定理1若马尔可夫过程的系统状态数量有限,且有 式中,N 为状态总数。当满足条件式(11),则称此时的马尔可夫过程处于极限状态,并且集合{p1,p2,…,pN}为马尔可夫过程的极限分布。 显然,当处于极限状态时,马尔可夫过程的概率分布满足 将式(12)代入式(9),结合全概率公式求解线性方程组,即可得到马尔可夫过程的极限分布,进而求解系统的可靠性指标。 由于电网电能波动较大且可靠性较低,轨道交通中的重要信号设备,如专用通信、综合监控、门禁、地铁应急通信系统等,一般配置2 套UPS 系统。每套UPS 系统均采用模块化结构,主要由旁路开关、若干个功率模块UPM(universal power module)和单片机控制静态切换开关MCU-STS(microcontroller unit-static transfer switch)组成。UPS 一般配置部分UPM 作为冗余备份,所有的UPM 和旁路开关的工作状态切换均受MCU-STS 模块的控制。正常工作时,市电从输入端输入,经过UPM 进行电能变换或经过旁路开关直接到达负载端。因此,MCU-STS 与所有UPM 和旁路开关为串联关系,而所有UPM 与旁路开关互为并联关系,若UPS 系统中配置n 个UPM,其中(n-k)个UPM 为冗余备份,则UPM 间构成一个k/n 表决系统。因此,模块化UPS 可以用可靠性模型框图描述,如图2 所示。 图2 模块化UPS 可靠性框图Fig.2 Reliability block diagram of modular UPS 在模块化UPS 系统中,每个UPM 与旁路开关及电池组都可以视为一个独立工作的不间断电源,每个UPM 的功率回路由整流、逆变和直流变换等环节构成,功率回路如图3 所示。UPM 的常用工作模式有整流-逆变模式、电池模式和旁路模式3 种。需要注意的是,同一模块化UPS 系统内所有投入运行的UPM 均工作在相同模式下。 图3 模块化UPS 功率回路Fig.3 Power loop of modular UPS ①整流-逆变模式:整流模块输入开关S1与逆变模块输出开关S2闭合,旁路开关断开,市电经过整流模块变换为直流电,既可以经过直流变换模块为电池充电,也可以经过逆变模块输出交流电至负载端。②电池模式:S1断开,S2闭合,旁路开关断开,市电失效,无法输入UPS,负载端通过电池组经过直流变换模块和逆变模块进行供电。③旁路模式:S1与S2均断开,旁路开关闭合,市电经过旁路开关直接到达负载端,UPM 内各模块均不工作。此时UPS 等效于短路,负载无法受到保护,将受到电网电压波动和断电的影响。 通常状态下UPS 工作于整流-逆变模式,若检测到市电波动大于其设定值,如市电断电等故障,则零间断切换至电池模式;若UPS 内部发生重大故障或需要人为检修,则切换至旁路模式。当UPS工作于电池模式时,检测到市电输入恢复正常后,零间断切换至整流-逆变模式;若在电池后备时间内,市电无法恢复正常,则在电池耗尽时强制切换为旁路模式。当UPS 工作于旁路模式,检测到UPS内部故障修复完成,则自动切换为整流-逆变模式。 投运设备的寿命周期中,其故障率可以用浴盘曲线模型进行描述,如图4 所示。在浴盘曲线模型中,设备的故障率可以分为早期失效、偶然失效与老化失效3 个阶段。其中,设备稳定运行时,其故障率处于偶然失效期,故障率很小且可认为属于常数,即偶然失效期的设备故障率近似于服从指数分布,此时,设备在任一时刻的故障率满足式(7),即认为处于偶然失效期的设备工作过程是一个马尔可夫过程。 图4 设备失效的浴盘曲线Fig.4 Bathtub curve of equipment failure 由于模块化UPS 的投运周期较长,在寿命周期中长时间处于偶然失效期,因此其工作过程可以视为一个马尔可夫过程[11],从而可得到其马尔可夫链,如图5 所示。图中:λ1为市电输入发生故障的概率,即市电故障率;λ2为电池后备时间内市电没有恢复的概率;λ3为UPS 内部UPM 失效数量大于(n-k)个的概率,其数值可通过单个UPM 故障率计算得到;μ1为电池后备时间内市电恢复正常的概率,即市电的修复率;μ2为人为修复排除UPS 内部故障的概率,即UPS 的修复率。 图5 模块化UPS 马尔可夫链Fig.5 Markov chain of modular UPS 如前文所述,轨道交通系统中重要的信号设备通常配置2 套UPS 系统,而每套UPS 系统包含若干个冗余备份的UPM,本文以每套UPS 系统配置5个UPM 为例进行分析。根据图5 所示的马尔可夫链,首先对单机模块化UPS 进行可靠性分析,而后推广至双机模块化UPS 并联系统,最后通过蒙特-卡罗法进行仿真验证。 利用状态空间法,根据图5 所示马尔可夫链,列写单机UPS 的状态转移矩阵,即 将式(13)代入式(12)和式(9),可求得 单机UPS 处于各工作状态的稳态概率,分别为 式中:P1为UPS 工作在整流-逆变模式的概率;P2为UPS 工作在电池模式的概率;P3为UPS 工作在旁路模式的概率。当UPS 工作在整流-逆变模式与电池模式时,由于负载供电受到保护,因此此时系统可用;当UPS 工作在旁路模式时,系统不可用,因此可得单机UPS 的可用度与不可用度分别为 当2 台模块化UPS 系统并机向负载端提供保护时,需要每台UPS 的容量均能承担全部负荷。假设2 台UPS 分别由单独的市电输入,其工作状态彼此独立。则根据每台UPS 内部是否正常工作以及市电输入是否正常,可以将双机UPS 负载分为6种状态,如表1 所示。 表1 双机UPS 系统状态Tab.1 States of double-UPS system 需要说明,由于单台UPS 切入旁路模式后,无法控制旁路电流以控制输出功率,因此当单台UPS内部发生故障时,首先由另一台UPS 承担全部负载,若2 台UPS 均需要切入旁路模式时,系统才切换至旁路模式。 由于2 台UPS 工作状态互相独立,每个状态的稳态概率均可通过式(14)~式(17)计算得到。由UPS 的工作模式切换逻辑可知,负载侧断电前系统必然工作在状态6,而状态1~状态5 到达状态6 有以下途径。 状态1→状态6:2 台UPS 分别发生内部故障,该事件发生的概率为 状态2→状态6:一台UPS 已经发生故障,另一台UPS 发生故障,由整流-逆变模式切换至旁路模式,该事件发生的概率为 状态3→状态6:一台UPS 由电池模式切换至旁路模式,另一台UPS 发生故障,由整流-逆变模式切换至旁路模式,该事件发生的概率为 状态4→状态6:2 台UPS 均从电池模式切换至旁路模式,该事件发生的概率为 状态5→状态6:一台UPS 已经发生故障,另一台UPS 由电池模式切换至旁路模式,该事件发生的概率为 以上5 个事件为双机UPS 系统转至旁路模式、负载不受UPS 保护的概率,而负载真正断电与否则由此时的市电是否发生故障决定,因而负载掉电的概率为 此时,该双机系统的可靠度为 由上述推导可知,当并机的UPS 数量增加时,其系统状态会呈指数级上升,导致系统复杂度大大提升,此时通过传统解析法已经难以进行精确的可靠性分析。因此在对大型UPS 系统进行可靠性分析时,常使用数值算法求解。 文献[10]最早提出了一种计算可靠性指标对设备故障率的敏感性分析方法。但该方法仅讨论了各可靠性模块串联的情况,对于并联模型和k/n 表决模型,所提出的方法并不适用。本节将根据文献[10]思路,将其推广至更具备一般性的k/n 表决系统。 根据可用度的定义,系统的可用度函数表示为 式中:x 为当前系统所处的状态;X 为当前系统所有状态的全集;P(x)为系统处于状态x 的概率;F(x)为功能函数,用于描述系统处于状态x 时可用与否,其定义为 该k/n 表决系统由n 个模块组成,则系统所处的状态x 可以表示为n 个模块状态的集合,即 系统对系统中模块xk的敏感度定义为:当模块xk的可用度发生无穷小变化Δak时,系统可用度函数对应的变化ΔA 与Δak的比值即为敏感度mk,表示为 对于k/n 表决系统,设其中n 个模块的状态概率分布相同,则系统处于状态i 的概率P(x=i)定义为 其中 由此可得式(33)中系统处于状态i 的概率变化量ΔP(x=i)为 将式(34)代入式(30),可得 式(35)中,当k=1 时,该k/n 表决系统等效为并联系统;当k=n 时,该k/n 表决系统等效为串联系统。此时式(35)简化为文献[10]提出的形式,说明本文推出的公式是文献[10]更具一般意义的形式。 采用蒙特-卡罗法对上文可靠性分析进行验证。该方法通过模拟大量随机过程,求解数学问题的近似解,具有收敛速度与模型尺寸无关、实现方法简单、结果直接等特点,广泛应用于可靠性分析的模拟中。 根据仿真过程中采用状态抽样或时间演化采样,蒙特-卡罗法可分为非序贯蒙特-卡罗法与序贯蒙特-卡罗法。其中,序贯蒙特-卡罗法模拟设备随时间运行的状态,属于时间跨度上的模拟,其逻辑框图如图6 所示。 根据图6 所示逻辑框图设计算法,对多机UPS并联进行分析。仿真参数设置如表2 所示。 图6 序贯蒙特-卡罗法逻辑框图Fig.6 Logical diagram of sequential Monte-Carlo method 表2 仿真参数Tab.2 Simulation parameters 假设市电输入与系统中所有设备的可靠性指标服从指数分布,分别对单机UPS 运行和双机UPS并联运行以及不同冗余配置进行仿真分析,得到故障率如图7 所示。由图7 可得,相比单机运行,双机UPS 并联运行的故障率更低,但在系统达到一定冗余量后,冗余量的提升对系统可靠性的提升并不明显,说明此时冗余配置已不是造成系统失效的主要原因。不同配置方式的失效前平均工作时间MTTF(mean time to failure)如表3 所示。 图7 不同配置的UPS 故障率仿真结果Fig.7 Simulation results of UPS failure rate under different configurations 表3 不同配置方式的MTTFTab.3 MTTF under different configurations 计算该UPS 系统中不同模块可靠性变化对系统可靠性的影响。根据图2 中UPS 系统的各层级,分别选取单个UPM、旁路开关、MCU-STS 模块3 个不同层级的部件进行比较,当其可靠性参数发生变化时,对变化前后的可靠性参数进行蒙特-卡罗法仿真,以分析其敏感性。敏感性参数设置如表4 所示。 表4 敏感性仿真参数设置Tab.4 Setting of simulation parameters of sensitivity 通过蒙特-卡罗法仿真,3 个部件改良前后的系统故障率如图8 所示。 图8 3 个部件改良前后故障率对比Fig.8 Comparison of failure rate among three units before and after improvement 由图8 中可见,MCU-STS 模块的可靠性对整个UPS 系统可靠性有较为显著的影响,而旁路开关与UPM 模块的改良对系统可靠性的提升较小。实际上,图8 的仿真分析结果与式(35)的理论分析结果是一致的。将仿真参数代入式(35),可得到各部件故障率变化对系统可用度的敏感性参数mk,如表5所示。 由表5 可知,从MCU-STS 模块到旁路开关到单个UPM,mk迅速减小,说明该UPS 系统中MCUSTS 模块对系统可靠性的影响最大,而采用50%冗余配置时,单个UPM 可靠性的改善对系统可靠性的影响较小。计算结论与蒙特-卡罗法的仿真结果相同,即:当单个UPM 的故障率下降时,系统的可靠性改善并不明显,但当MCU-STS 的故障率得到同等幅度的减少时,系统故障率减少得非常显著。 表5 各部件敏感性参数Tab.5 Sensitivity parameters of different parts 蒙特-卡罗法的仿真结果显示,当负载配置冗余更多时,UPS 的可靠性将得到较大提升,能有效减少负载断电带来的损失。然而,配置更多的UPM不仅需要更高的配置成本,而且其运行成本也随之增加。因此,有必要从多个角度对UPS 冗余方案的成本进行评估。 文献[6]介绍了一种计及时间成本的经济成本计算方案,但没有考虑UPS 的运行成本,而模块化UPS 运行中产生的损耗会受其运行方案影响。因此,在文献[6]的基础上,本文提出了计及时间成本与运行成本的经济成本计算方案,即 式中:Mi为配置UPS 的成本;Mf为在UPS 寿命内负载断电造成的损失;Ms为在UPS 寿命内日常维护与运行造成的功率损耗成本。其中Mf和Ms的计算公式分别为 式中:M0为初始时刻负载断电的经济损失;Mp为每年维护与检修的成本;SUPS(t)为UPS 整机的损耗功率,与UPS 的运行方式有关;R(t)为t 时刻的电价。 当UPS 系统中改用可靠性更高的元件,系统可靠性将得到改善,但配置成本Mi也随之上升。为了描述可靠性与经济成本的关系,本文提出风险成本回收时间tr的指标。tr表示该UPS 系统的配置成本、运行成本逐渐分摊负载失电造成的经济损失所需的时间,其定义为 以本文所提出的UPS 信号电源系统为例,其经济性分析如表6 所示。 表6 UPS 系统经济性分析Tab.6 Economic analysis of UPS system 由表6 计算结果可得,对于单UPS 配置方案,在投入运行约3.36 年后可以回收其风险成本,因此在采用该配置方案时,通过提高监测与检修频率,尽可能保证工作前5 年内的正常运行,是回收风险成本的重点。 当UPS 系统的运行方式改变,则其故障率与损耗功率均会发生改变,代入可靠性参数即可计算不同UPS 冗余方案的经济成本,并根据成本做出合理的决策。 本文针对分布式模块化UPS 的结构特征和工作模式,提出了模块化UPS 可靠性评估的框图模型,并分析了不同模块对系统可靠性的敏感性指标,最后结合UPS 的经济性进行了综合分析,提出从可靠性、敏感性和经济性多方面综合考虑的UPS 配置方法,对UPS 配置方案的设计有一定的指导作用。 本文是以轨道交通信号系统模块化UPS 的配置为例进行分析的。实际上,对于其他需要配置UPS 的应用场合,如医院、银行、数据中心等,其冗余配置方法与系统结构类似,仅在负载需求与负载端连接方式上存在一些不同,因此,同样可采用本文方法进行可靠性与经济性分析。因而,本文提出的方法具有普适性。


1.2 基于马尔可夫链的可靠性分析方法
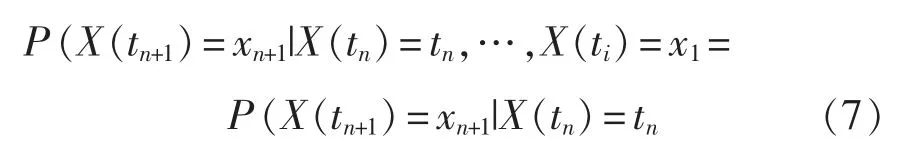

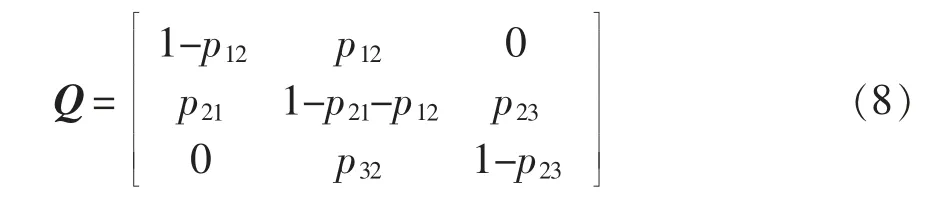


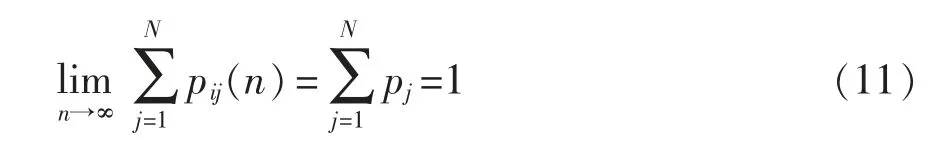

2 模块化UPS 的马尔可夫过程分析

3 模块化UPS 系统的可靠性分析
3.1 单机模块化UPS 可靠性分析



3.2 双机模块化UPS 并联系统可靠性分析








3.3 UPS 可用度的敏感性分析




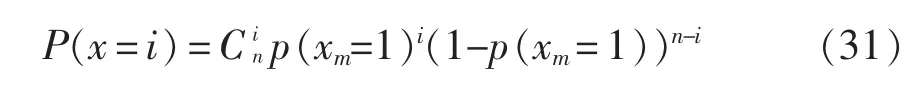


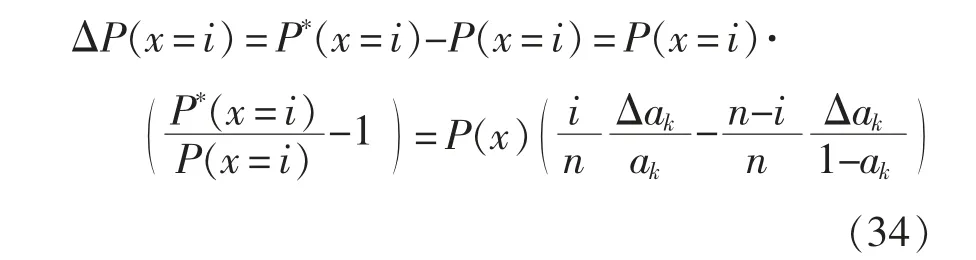
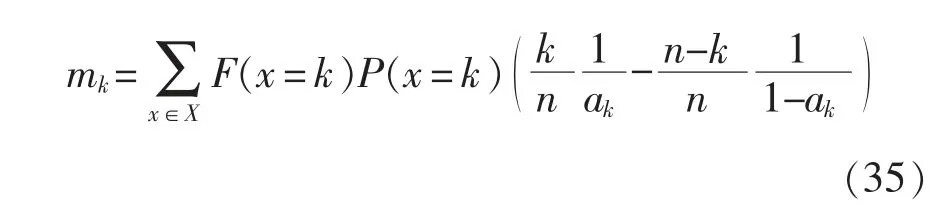
4 可靠性分析验证



5 模块化UPS 经济性分析




6 结语

