考虑线路运行环境的牵引变流器IGBT寿命评估
黄先进,杜田倩,李 鑫,穆 峰
(北京交通大学电气工程学院,北京 100044)
在轨道交通中,四象限变流器是列车的重要设备之一,而IGBT 又是变流器的核心器件,列车在行驶过程中有自身运行工况的改变以及环境工况的改变,而结合两者分析IGBT 寿命的相关文献较少。文献[1]研究了基于运行图的多列车运行控制的方法,考虑了坡道、隧道、曲线等线路条件,并设计了多列车牵引计算的仿真软件,为列车运行图的设计和调整提供了理论上的支撑;文献[2]以IGBT 为研究对象,基于列车运行状态的改变,通过电机转速和转矩的变化,建立牵引传动系统的仿真模型,对IGBT 的寿命进行了完善地分析;文献[3]基于高速动车组的任务剖面,在牵引计算中考虑了坡道等线路条件,通过计算得到变流器的功率变化情况,进而建立电热联合仿真模型,得到了IGBT 的预测寿命。文献[1-3]均缺少气压、温度、湿度等环境因素对IGBT 器件寿命影响的分析,且忽略了实际热网络模型和理想热网络模型对IGBT 器件寿命的影响。文献[4]详细地从有限元模拟中提取了Foster 网络模型的参数,建立PLECS 模块与Simulink 的电热联合仿真,从仿真设计上提高了功率模块温度预测的精度;文献[5-7]介绍了瞬态双界面法测量IGBT热阻抗参数的方法,从实验测量上提高了功率模块温度预测的精度,因此,为了更加真实地评估IGBT的可靠性,应对IGBT 的热阻抗进行测试;文献[8-10]总结出目前较为成熟的IGBT 寿命计算流程,首先由IGBT 的电压、电流进行损耗计算,损耗经热网络模型得到IGBT 的结温,然后结温经雨流算法统计出温度波动,最后,温度波动经寿命模型计算损伤度。
综上所述,为了研究变流器运行工况下IGBT的可靠性,应至少考虑列车的运行线路条件、列车的运行环境、IGBT 真实的热阻抗参数,这些因素均会影响IGBT 的结温,而IGBT 结温又与IGBT 的寿命息息相关。本文研究基于变流器运行工况的IGBT 寿命评估流程,为变流器的散热设计和IGBT寿命分析提供理论上的支撑。
1 环境工况
变流器IGBT 的寿命受列车运行工况和环境工况的影响。在考虑环境因素时,海拔、气压、温度和湿度是影响变流器IGBT 散热的主要因素,IGBT 的散热结构如图1 所示,IGBT 的热网络模型如图2所示。

图1 IGBT 结构模型Fig.1 Structural model of IGBT
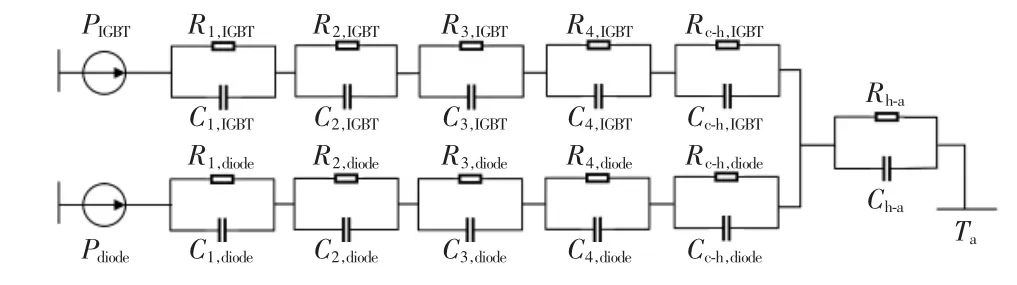
图2 热网络模型Fig.2 Thermal network model
目前列车变流器常用的冷却方式有风冷、水冷以及风冷和水冷相结合的方法,IGBT 热量传递的基本方式有传导、对流、辐射,在变流器散热中辐射的比重较少,因此主要考虑热传导和热对流的影响。在计算IGBT 的寿命时,无论是哪种冷却和传热方法,最终都将散热到外界环境,因此外界环境的条件是有必要考虑的。
文献[11]中将热源到环境之间的散热模型等效为多个热阻的串联和并联,散热器到环境之间的热阻是散热器基板到环境的热阻和散热器肋片到环境的热阻之和。但仅仅考虑热阻并不能完全等效出功率器件到环境之间的散热情况,为了更加接近实际的散热情况,需要添加热容来表示瞬态的散热。
空气热导率λ 的表达式为

式中:ρ、R、T 和P 分别为空气密度、气体常数、温度和压强;P0为标准大气压101.325 kPa ;l 为气体分子2 次碰撞间的平均自由行程;u¯为气体分子运动的平均速度;cv为气体的比定容热容。除了压力很低(<2.67×10-3MPa)或压力很高(>20×103MPa),均可以认为空气的热导率不随气压变化。
在0~200 ℃可以不考虑温度对比热容Cm的影响。计算空气的定压摩尔热容为
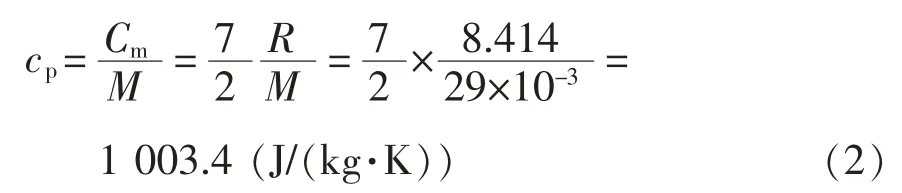
式中:cp为空气的定压摩尔热容;M 为摩尔质量。
空气热容C 的表达式为
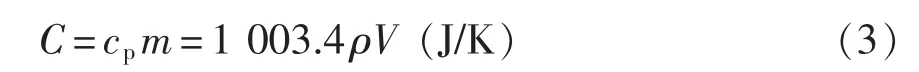
式中:m 为空气的质量;V 为空气的体积。
2 基于牵引计算的变流器仿真设计
基于列车运行工况和环境工况的变流器评估中,IGBT 的寿命是一个关键性问题。以变流器的功率变化数据建立变流器的Simulink 电仿真模型,通过PLECS 模块建立变流器的热仿真模型,在电仿真中得到IGBT 的驱动信号,输入到热仿真模型中的IGBT,组成电热联合仿真模型。基于变流器运行工况的IGBT 寿命评估流程如图3 所示。

图3 IGBT 寿命的研究流程Fig.3 Research process of IGBT life
列车在运行的过程中,不同的运行状态对应不同的合力,具体表示为

式中:c 为列车的合力;f 为列车的牵引力;ω 为列车的阻力;b 为列车的制动力;ω0为列车的运行阻力,包括基本阻力和附加阻力;ω1为列车的基本阻力;ω2为列车的加算坡度阻力,是曲线阻力、隧道阻力、坡度阻力等的加和;A、B、C 为常数;v 为列车速度。
线路的数据和列车的运行数据不易获取,因此可采取无级牵引和制动的方法。假设加算坡度为1,对列车CRH3 的牵引曲线和制动曲线进行分段拟合,拟合结果分别如图4 和图5 所示。

图4 牵引曲线的拟合Fig.4 Fitting of traction curve
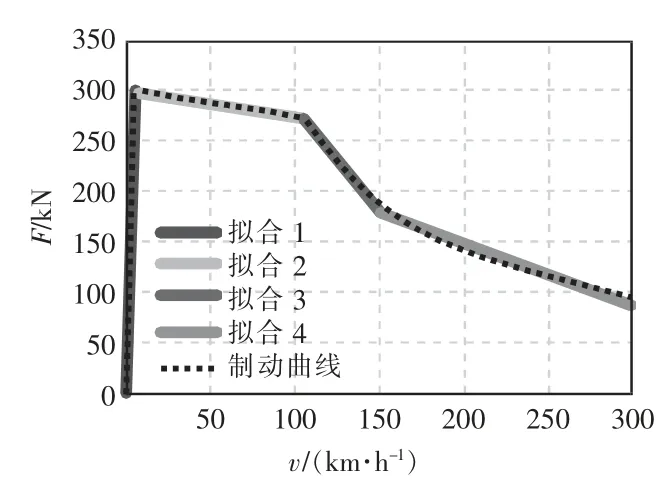
图5 制动曲线的拟合Fig.5 Fitting of braking curve
牵引和制动的拟合函数表达式分别为
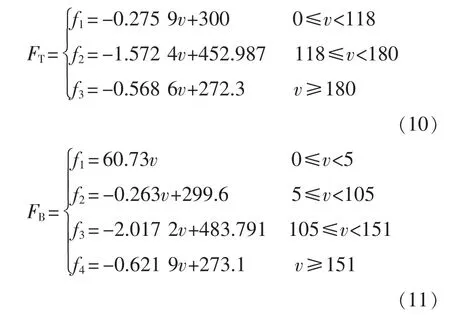
式中:FT为牵引拟合函数;FB为制动拟合函数。
首先求取列车速度的变化,对列车的加速度在时间上进行积分,得

式中:mstatic为列车的静态质量,t;mdynamic为列车的动态质量,t。代入牵引拟合函数表达式,并在等式两边求导,可得

同理,可列出列车制动阶段的速度表达式。设定列车的运行过程为:牵引-巡航-惰行-制动,可得列车的速度变化曲线,如图6 所示。
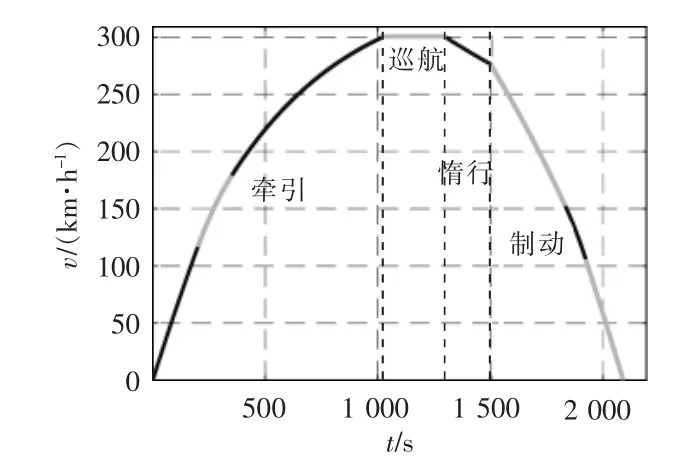
图6 速度-时间曲线Fig.6 Speed-time curve
力与速度的乘积可得列车电机侧的功率,其变化曲线如图7 所示。

图7 列车电机侧的功率变化曲线Fig.7 Power variation curve on the motor side of a train
CRH3 列车中有4 台辅助变流器,其中2 台单辅变流器为160,另外2 台双辅助变流器为320[12]。单台变流器的总功率PM的计算表达式为

式中:PV为整车功率;PA为辅助变流器的功率;η1、η2、η3为牵引的效率为制动的效率。
根据式(10)计算单台整流器的功率随时间的变化,如图8 所示。采用瞬态电流控制策略,结合变流器直流侧的功率或电流情况设计电仿真模型。

图8 单台变流器功率曲线Fig.8 Power curve of one single converter
3 变流器IGBT 热参数测试
目前IGBT 的热参数测量主要有2 种方法:一是热电偶法,二是瞬态双界面法。热电偶法对IGBT的热阻抗定义为

式中:Zth(t)为IGBT 的热阻抗;Tj(t)为IGBT 的瞬态结温;Tc(t)为IGBT 的瞬态壳温;Vce为IGBT 模块达到热平衡的集射极电压;Ic为IGBT 达到热平衡的直流电流。
热电偶方法最大的缺点在于壳温的测量,对于型号为FZ750R65KE3 大功率IGBT 模块,外壳的表面积较大,测量不同位置的壳温会存在误差,所以本文采用瞬态双界面法。
瞬态双界面法对于IGBT 的热阻抗定义为
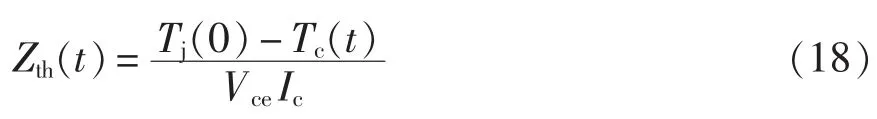
式中,Tj(0)为IGBT 的初始结温。
IGBT 的内部结温不易测量,因此需要选取一个温敏参数体现结温,常用的温敏参数为栅极-发射极电压Vge或Vce。Vce与Tj之间的关系线性度更好,因此本文选取Vce作为温敏参数,测试实验平台如图9 所示。首先,需要测试750 mA 下IGBT 的导通压降Vce与芯片结温Tj的关系。Vce与Tj的线性拟合曲线如图10 所示。

图9 测试实验平台Fig.9 Test experiment platform

图10 Vce 与Tj 的线性拟合曲线Fig.10 Linear fitting cure of Vce and Tj
IGBT 饱和压降Vce与结温Tj之间的函数关系为

在测量IGBT 的热阻抗时,认为内部的传输路径是相同的。达到IGBT 模块外壳后,需要设置不同的外部散热环境,由于IGBT 模块与散热器之间存在空气层,热阻较大,可以通过涂抹硅脂使IGBT 模块与散热器两者紧密接触,但硅脂过多会起相反效果。在实际的实验操作中发现,通过拧紧IGBT 与散热器之间的固定螺丝,也可以达到两者紧密连接的效果。有、无硅脂的外部环境的测试结果可能存在偶然性,所以采用无固定有硅脂、有固定无硅脂和无固定无硅脂3 组实验数据进行对比,实验结果如图11所示。由图11 可见,在3 种不同外部散热环境下用同一个电流进行加热,达到的热平衡是不同的。
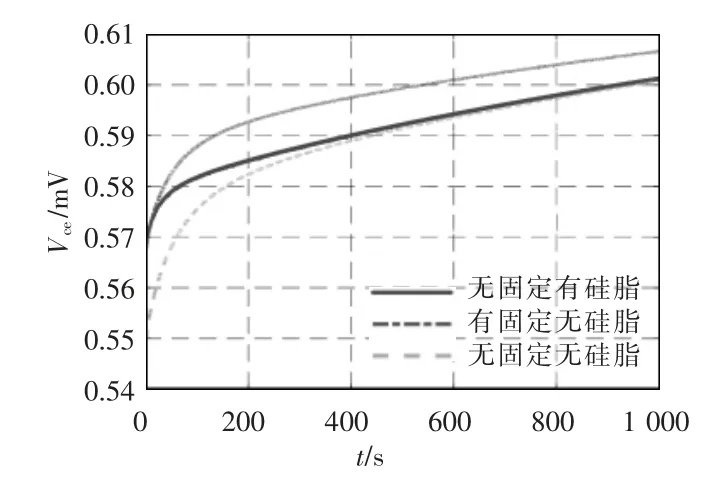
图11 Vce 的变化曲线Fig.11 Variation curves of Vce
利用式(13)可将IGBT 的Vce与时间t 的关系转化为IGBT 结温Tj与时间t 的关系,如图12 所示。图中,在无固定有硅脂与有固定无涂硅脂2 种散热环境下,IGBT 达到的热平衡相差较少,IGBT 的结温也基本相同,而无固定无硅脂的IGBT 模块的外壳与环境之间热阻较大,因此与环境之间的温差更大,IGBT 的结温也更高。

图12 Tj 的变化曲线Fig.12 Variation curves of Tj
利用式(18)将结温Tj与时间t 之间的关系转化为IGBT 热阻抗Zth与时间t 之间的关系,如图13 所示。图中,3 种散热条件下的热阻抗在前期基本重合,这是因为3 种散热条件下IGBT 模块内部的散热路径是一致的,分离点就是IGBT 外壳外部的散热环境不同所导致的。选取重合的曲线,利用Matlab4 阶指数模型进行拟合,IGBT 达到稳态时,散热的好坏取决于热阻的大小,4 阶热阻相加的数值为9.307 3 K/kW。已知型号为FZ750R65 KE3 的IGBT 的理想热阻为8.7 K/kW,可知,目前IGBT 的老化程度为6.98%;热参数的测量提高了IGBT 热网络模型的精确度,计算的IGBT 寿命更加贴近实际寿命。

图13 Zth 的变化曲线Fig.13 Variation curve of Zth
4 变流器IGBT 寿命预测
实际列车中IGBT 模块被封装在变流器中,只能依托于仿真软件和方法分析得出变流器中IGBT的寿命情况,进而判断变流器中IGBT 是否需要更换,因此,软件的设计和方法精确度对IGBT 真实寿命评估的准确性起着很重要的作用,利用Simulink与PLECS 搭建电热联合仿真模型,如图14~图16所示,并将英飞凌提供的器件热模型导入到PLECS中。仿真结果分别如图17~图23 所示。

图14 IGBT 开通损耗的模型Fig.14 Model of IGBT turn-on loss

图15 IGBT 关断损耗的模型Fig.15 Model of IGBT turn-off loss

图16 Vce 和Ic 关系Fig.16 Relationship between Vce and Ic
由图17~图23 可见:IGBT 的结温情况与列车工况情况相对应,第1 阶段为随着列车速度的提升,牵引功率增大,IGBT 的结温开始上升;第2 阶段为随着列车开始巡航,牵引功率大致稳定,IGBT的结温波动也较小;第3 阶段列车开始惰行,惰行时变流器的功率较小,IGBT 的结温开始下降;第4阶段为列车开始制动,IGBT 的结温与制动功率的变化趋势一致。

图17 IGBT 的集射极压降Fig.17 Collector-emitter voltage drop of IGBT
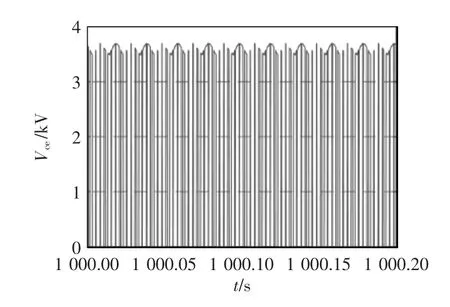
图18 IGBT 集射极压降局部放大图Fig.18 Partial enlarged view of IGBT collector-emit ter voltage drop

图19 IGBT 的集电极电流Fig.19 Collector current of IGBT

图20 IGBT 的集电极电流局部放大图Fig.20 Partial enlarged view of collector current of IGBT

图21 IGBT 开关一次的损耗Fig.21 Loss of IGBT switching once

图22 IGBT 的导通损耗Fig.22 Conduction loss of IGBT

图23 环境温度为25 ℃的IGBT 结温Fig.23 IGBT junction temperature with an ambient temperature of 25 °C
应用手册中给出了IGBT 的TC 图,相较于经验取值更具有参考性。选取最大结温为150 ℃的曲线进行线性拟合处理,可得到
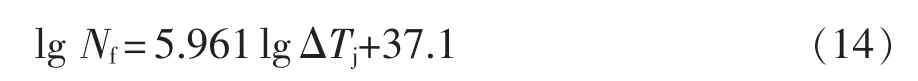
式中:Nf为循环失效周期数;ΔTj为结温波动。
基于设定路线的仿真情况,利用雨流算法对IGBT 的温度波动进行统计,结果如图24 所示,可得到温度的变化周期数、温度的变化范围、温度在一个周期内的平均值、温度的起始时间和温度的终止时间,这5 个指标一一对应。在计算得到Nf后,IGBT 采用的线性累积损伤模型为

图24 25 ℃的雨流统计Fig.24 Rainflow statistics at 25 ℃

式中:CL_IGBT为IGBT 的损 伤度;Nf,n为第n 次 热循环所对应的循环失效周期数;Nn为所对应实际的热循环次数。当器件损伤累积到一定程度即CL=1 时,表示IGBT 失效。将雨流统计结果代入式(14)和式(15),可得到基于设定路线下IGBT 的损伤度为C=1.606 7×10-10。
5 结语
本文研究了列车运行工况和环境工况对IGBT寿命的影响。以牵引计算为基础构建了列车的运行图,并设计了变流器的电仿真模型。在构建热仿真模型前测试了IGBT 的实际热网络参数,使IGBT的寿命评估结果更加符合实际情况。最后搭建了Simulink 与PLECS 的电热联合仿真模型,观测了IGBT 在列车运行过程中的电流、电压、结温、损耗的变化,利用雨流算法统计了结温的波动数,计算了IGBT 基于变流器运行工况的损伤度,为实际应用中变流器IGBT 在列车不同的运行工况和环境工况的寿命评估提供了研究流程。

