高速动车组轮径差与牵引电机功率及温升耦合性研究
于 勇,马周聪,刘亚云
(中车青岛四方机车车辆股份有限公司国家级技术中心,青岛 266000)
高速动车组运用数据表明,在运用过程中,由于动车组本身轮对踏面接触疲劳及线路原因不同会造成轮对踏面磨耗量不同,导致出现全列轮对轮值相差较大的情况,当轮径差达到一定程度后,将对车辆系统的动力学性能产生显著影响。在动车组运营进入特殊路段或者动车组即将进入轮对镟修前,极易引起动车组报牵引电机温度高的风险,需及时进行轮对镟修,以消除轮径差。
关于动车组轮对磨耗和牵引电机负荷分配不均的影响,国内外学者和设计师已进行相应的分析与论证。针对该问题,需在保证安全性的前提下,统筹考虑经济性,制定出相邻车辆、同一车辆及同一转向架轮径差镟修限度标准,指导动车组检修运用。
目前,西南交通大学王珍[1]在理论上对高速动车组不同轮径差的负荷进行分析,得到了相应的镟修标准及相关优化决策模型;西南交通大学金学松等[2]针对高速动车组牵引参数建立车辆系统动力学模型,详细分析了高速车辆轮对的轮径差的改变对直线运行稳定性、运行平稳性和曲线通过性能的影响;池茂儒等[3-4]分别从行车安全性和车辆系统稳定性的角度对轮径差的影响进行分析,表明反相轮径差对行车安全性影响较大,并根据轮径差大小对车辆系统稳定性的影响分为稳定区、欠稳定区和亚稳定区,在亚稳定区内车轮容易发生轮缘偏磨;西南交通大学翟婉明等[5]结合车辆-轨道耦合动力学理论,提出高速铁道设计中轮轨系数最优动力性能;梁大伟、杨其林等[6]针对轮径差对牵引系统的影响进行了理论分析,结合YJ258 型牵引电机,进行轮径差与牵引电机负荷不平衡的关系分析,并给出轮径差超限后的保护措施。
在理论分析的基础上,国内外学者结合仿真对理论进行了验证。大连交通大学陈汝义等[7]结合Matlab-Simulink 仿真模型,对所观测的轮径差异及电机参数差异对电机电流偏差的影响和规律进行了仿真分析和理论验证;Zou Ruiming 研究团队[8]分析了轮径差对轮对受力状态和运动规律的影响,通过模型仿真,分析了在惰行工况和动态制动工况下,轮径差对轮轨动态接触关系的影响;通过对同一转向架两种典型轮径差的研究,提出了同一机车轮径差的几种特殊工况,分析了不同工况和同工况不同轮径差对机车直线运动性能的影响[9];Chen Rong 团队[10]针对轮对的齿形磨损和加工误差造成的不同车轮滚动半径偏差进行了理论分析,结合运用迹线原理和有限元方法仿真模型搭建,分析了不同轮径差的失稳稳定性;国外学者Sawley K、Urban C 和Mace S、Pena R 等[11-13]研究分析了踏面凹形磨耗对轮径差的影响规律,得出踏面凹形磨耗产生轮径差曲线的倾斜,在动车组运行过程中极易造成轮缘贴近钢轨,容易产生两点接触,严重影响车辆运行稳定性。但是,针对轮径差带来的实际牵引电机温升,目前没有结合理论仿真计算和试验结果对比的深入研究。
本文在分析采用车控方式运行动车组牵引系统的基础上,提出一种“轮径差-功率温升”分析法,并建模进行计算仿真,在此基础上预置带有规定轮径差的轮对进行滚动台架试验,试验结果与理论仿真结果符合,验证了该“轮径差-功率温升”分析法的准确性和可信性,对动车组镟修及预测与健康管理系统PHM(prognostics and health management)起指导作用。
1 控制原理及分析
国内各平台高速动车组均采用单相AC25 kV/50 Hz 高压供电,经牵引变压器降压后引入牵引系统。中国高速铁路CRH(China railway highspeed)系列动车组牵引传动系统,采用单台逆变器驱动2 个转向架共4 台异步电机并联运行的方式,即“车控”方式,以达到简化结构、降低成本以及减轻质量的目的。在电机并联运行方式下,当各牵引电机的转矩-转速特性完全相同时,变流器以各台电机的三相电流、各台牵引电机转速取平均值作为双闭环控制的输入,而作用到同一动车内各台电机上的电压U 的频率fs和幅值完全相同。在牵引电机和轮径一致的情况下,通过控制保障各台电机输出功率基本一致。当动车组存在轮径差ΔD 时,各牵引电机以不同的转差率s 工作,导致同一动车内4 台电机速度差异Δv,并带来电流差异Δi,导致电机的转差s1、s2、s3、s4存在一定差异。同时,由于存在轮径和电机参数的差异,导致电机间的输出转矩发生偏差,且平均转矩输出与指令值之间也会存在稳态误差,当牵引电机的阻抗不同时,电机温升不同,这种由于轮径差异引起的电流和功率分配不均衡无法通过软件控制消除,影响列车牵引性能的发挥。高速动车组在牵引工况时,轮径较大的轮对对应牵引电机发挥的转矩大、电流大、温升高,但转子电阻随温度增加而加大时,转矩-转速特性移动,在相同转差率下的电流减少,并阻碍温度的上升,从等效热路方面看,这种相反的作用趋势,有利于缓和轮径偏差的影响。轮径偏差、电机电流i 及转差率s 关系的相互影响如图1 所示,其中,M 为电机转矩。
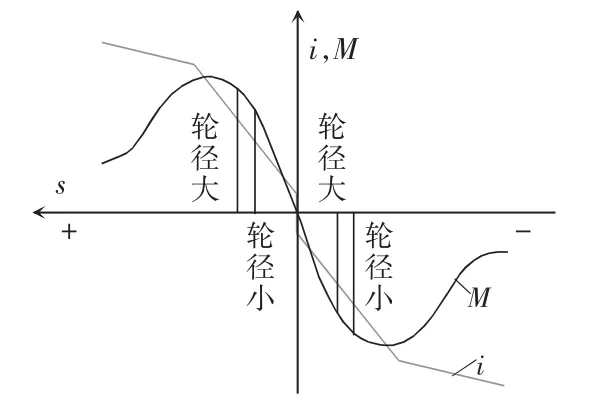
图1 轮径偏差的影响Fig.1 Influence of wheel diameter difference
高速动车组车控模式采取4 台牵引电机并联供电的方式,电机供电电源电压幅值、频率一样。牵引控制单元TCU(traction control unit)控制模块采集各台并联电机速度(取均值)和电流总和(送入控制模型求取均值)。车控模式下的牵引变流器将各台电机(速度目标设定值一致)等效成一台等效平均电机来进行控制,车控模式下电机控制框图如图2所示。电机等效电路原理如3 所示,图中,I 为电机定子电流,U 为相电压,Rs为定子绕组电阻,Xsδ为定子绕组漏电抗,Xr'δ为归算到定子侧的转子漏电抗,Xm为励磁电抗,R'r为归算到定子侧的转子电阻。
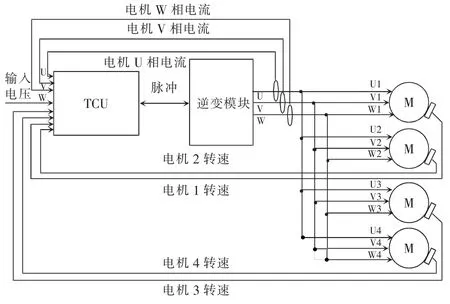
图2 车控模式下电机控制框图Fig.2 Block diagram of motor control in vehiclecontrol mode
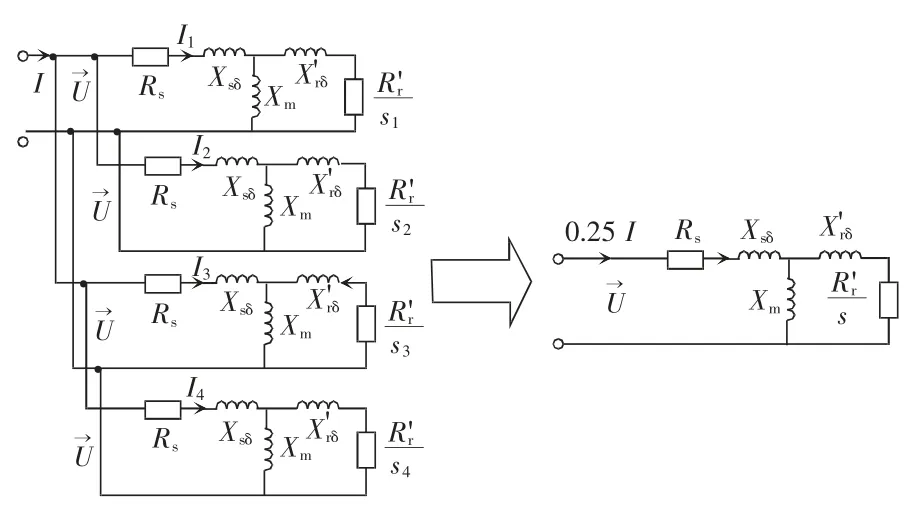
图3 电机等效电路原理Fig.3 Schematic of equivalent circuit of motor
1.1 控制模式对额定转差率的要求、理论模型及分析
CRH 系列高速动车组多采用直接转矩控制DTC(direct torque control)和矢量控制FOC(field-oriented control)。三相鼠笼异步牵引电机发挥的功率实际和转差率的关系不受牵引变流器控制算法的影响,以直接转矩控制为例,通过滞环控制器检测到电机电压及电流,并将对磁通与转矩的设定作为控制的目标值,利用二者在控制过程中的控制误差直接驱动逆变器的功率器件工作,在控制转矩后,同时控制电机的速度。直接转矩控制和矢量控制的电机控制原理如图4 所示。
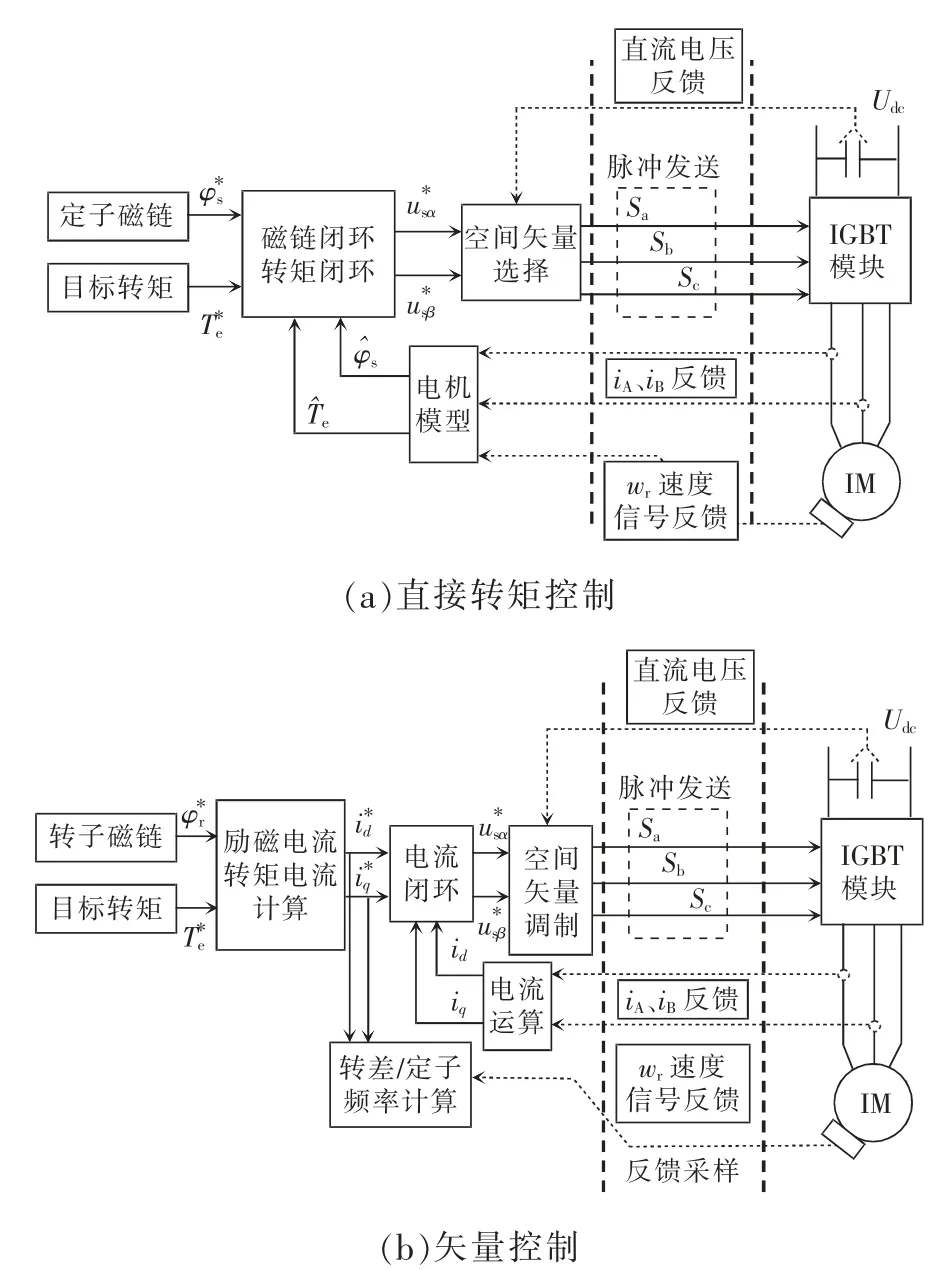
图4 电机控制原理Fig.4 Schematic of motor control
在转子磁链定向控制的异步牵引电动机中,牵引电机的电磁转矩可表示为

式中:Te为电磁转矩;P 为电机输出功率;Lm为电机互感;Lr为转子电感;Ψr为转子磁链;iqs为dq 旋转坐标下q 轴定子电流,是定子电流空间矢量在转子磁链空间矢量定向坐标系中的虚部分量。
在方波控制情况下,牵引变流器输出电压幅值和频率固定,加载到电机定子上的电压幅值和频率也固定,各电机实际输出功率只受其转速差异影响。基于以上控制模型分析,直接转矩控制在车控模式下,电机额定转差设计与电机参数相关。
根据感应电机的等效电路可知,定子传递的穿过气隙的总功率可表示为

因此,穿过气隙传递给转子的总功率中,1-s 部分转变成了机械功率,s 部分作为转子导体中的I2R被消耗掉,类似转子中消耗的功率可以表示为

1.2 轮径差对牵引、再生制动工况下控制的影响及其分析
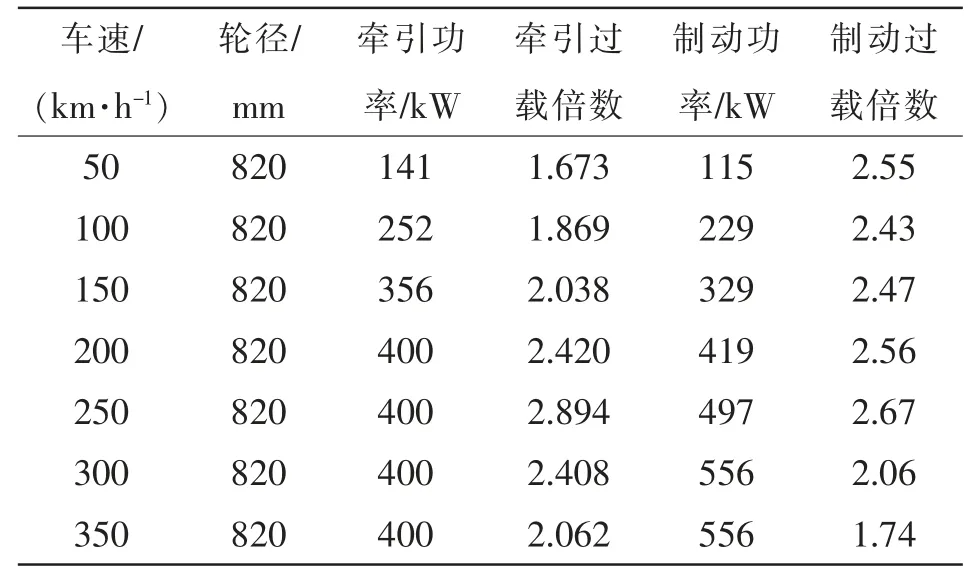
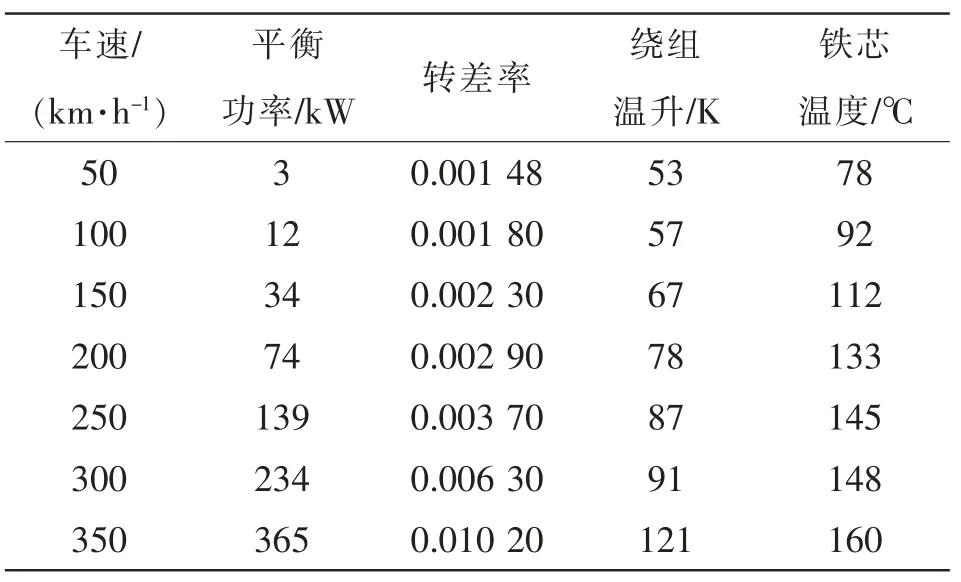
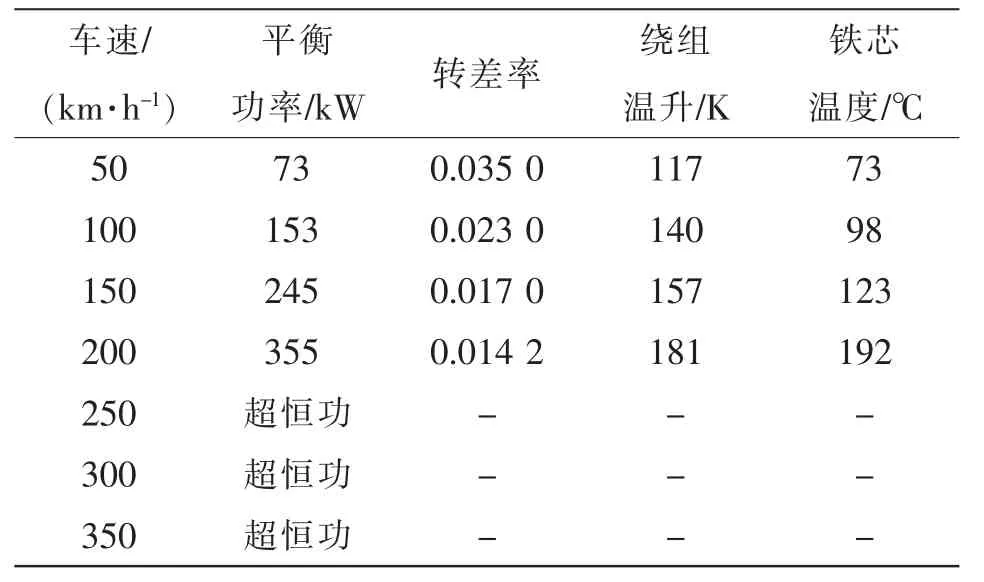
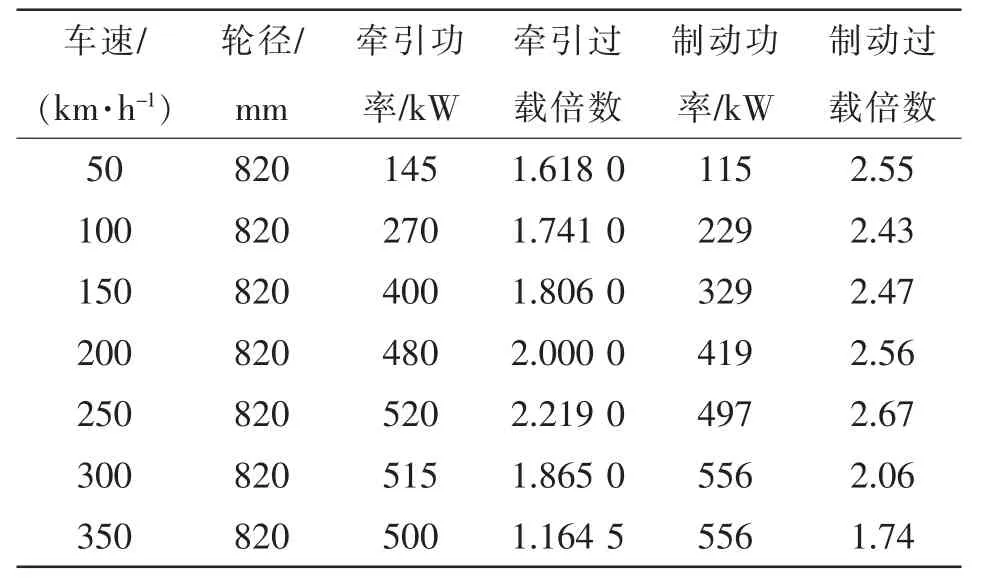
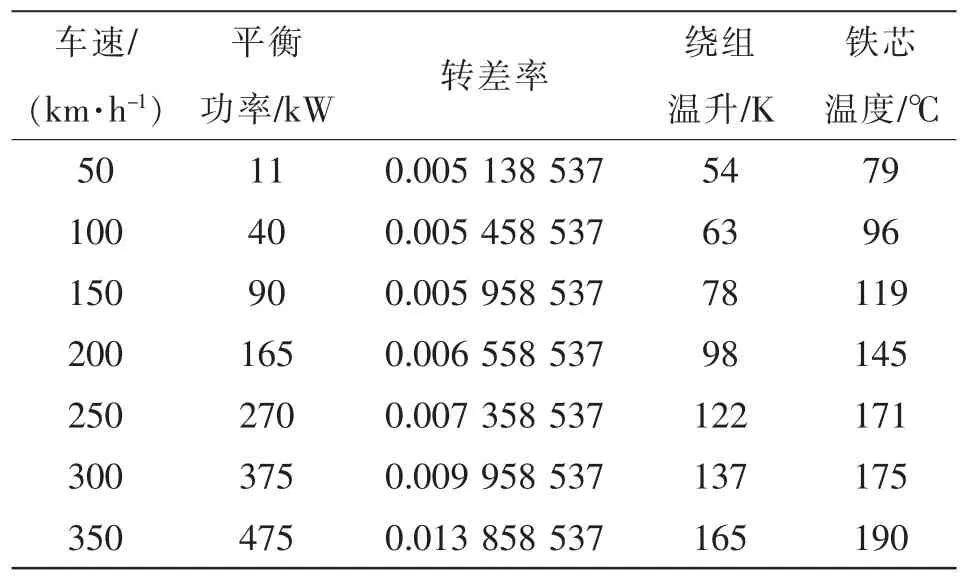
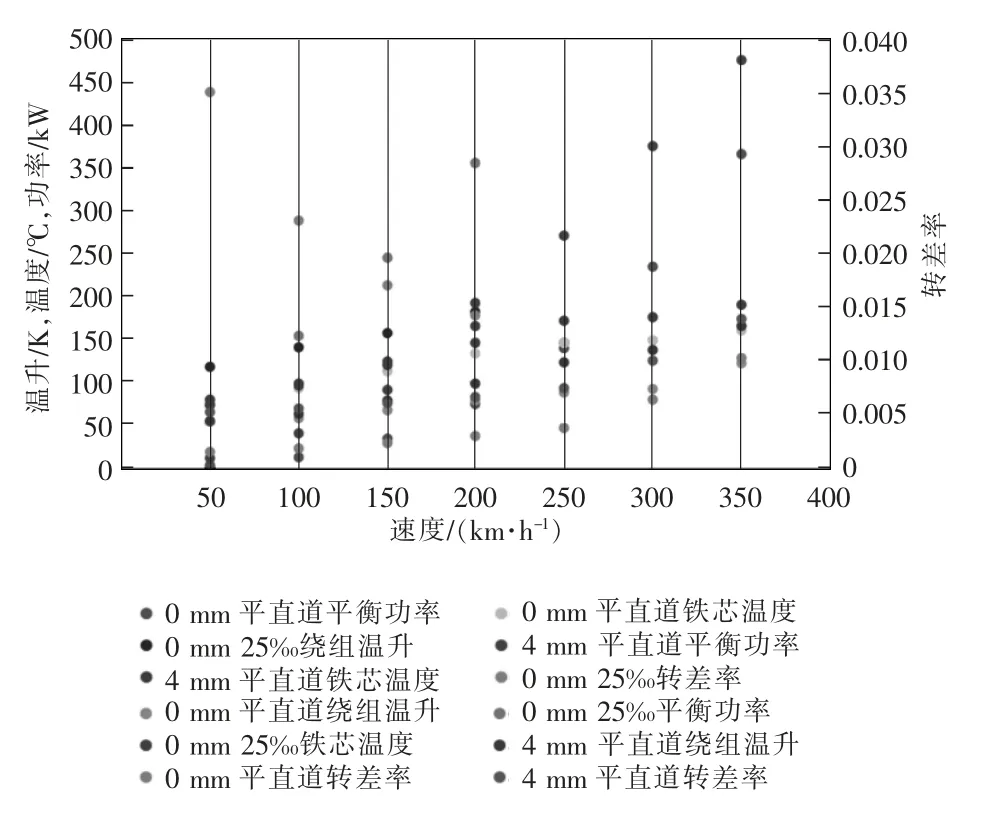
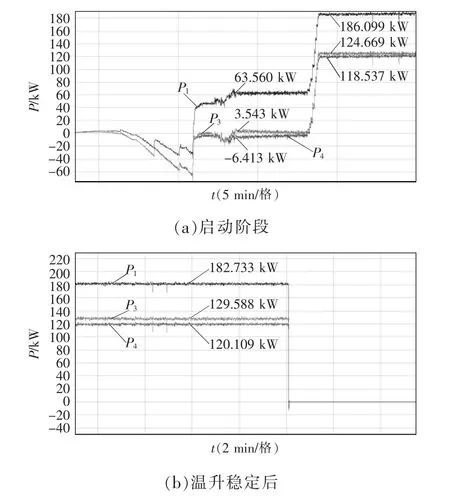
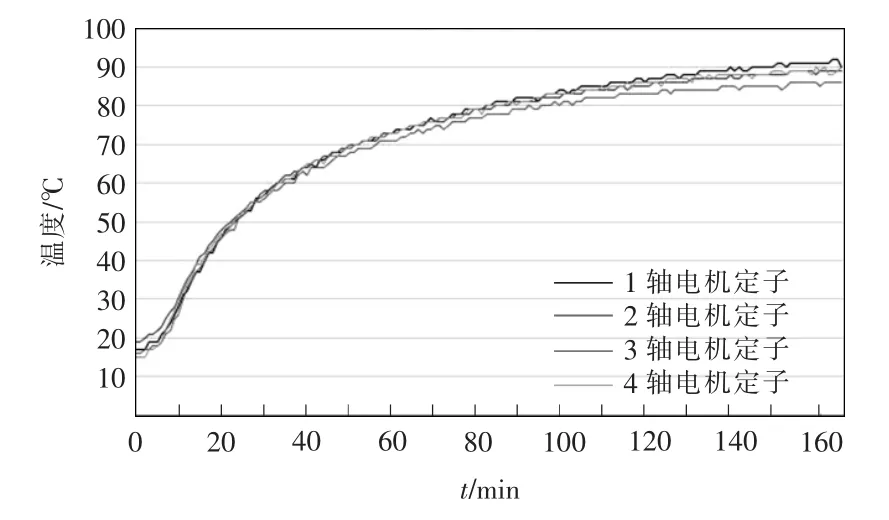
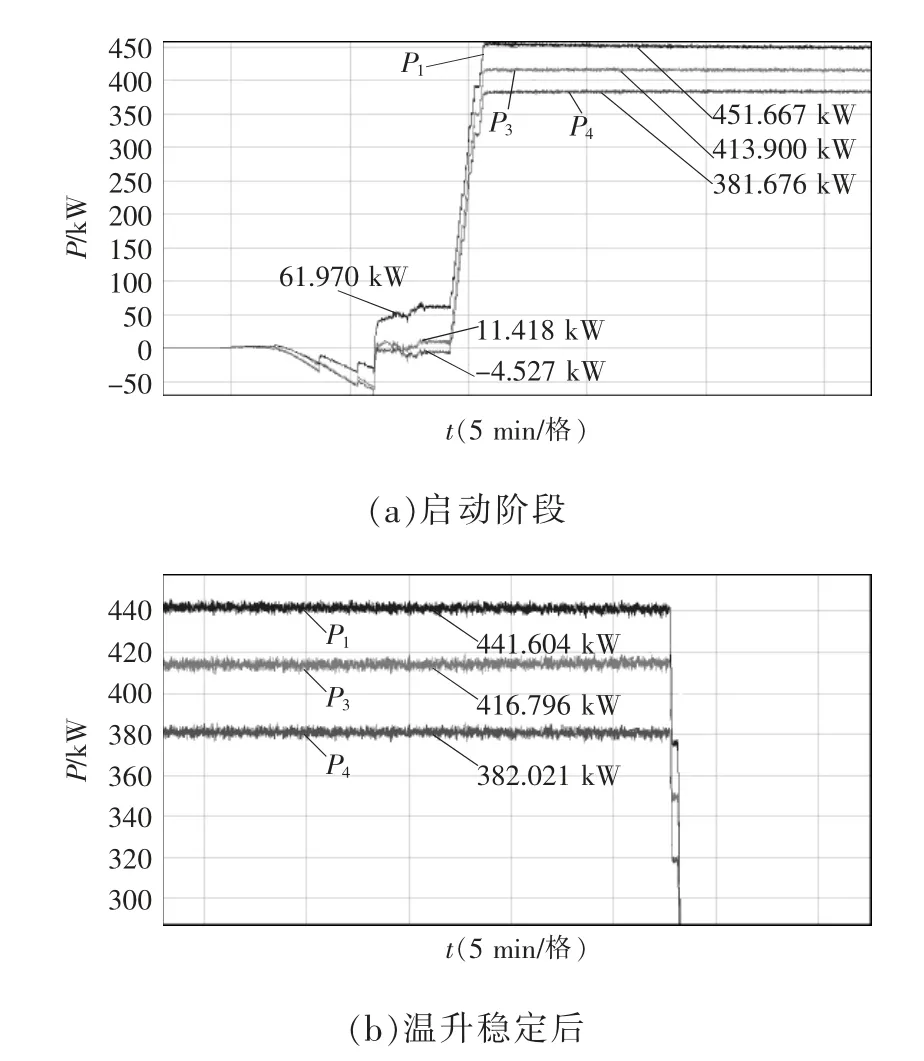
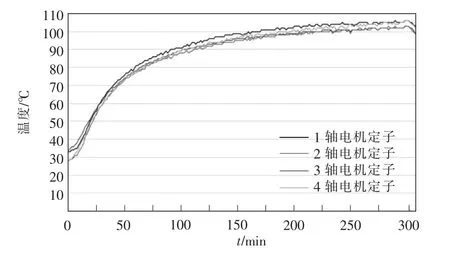
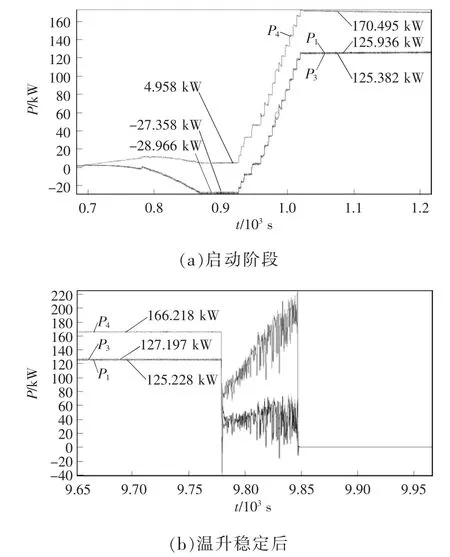
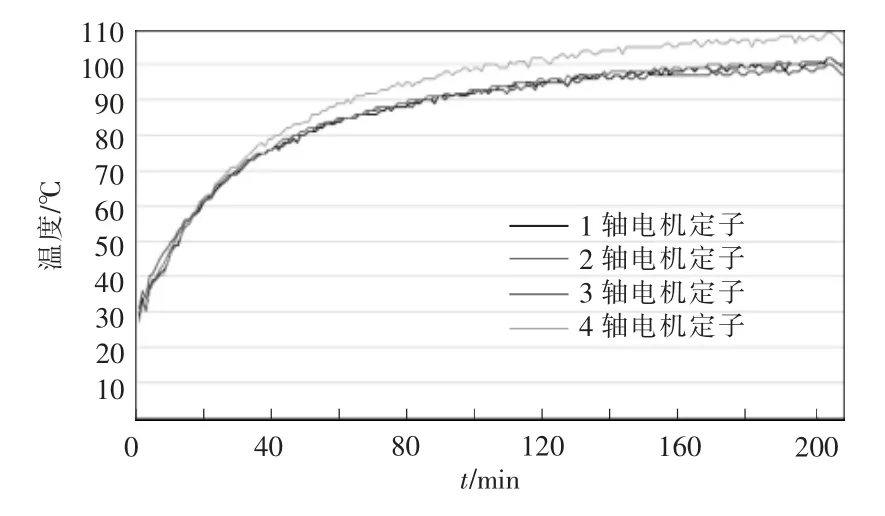
当牵引变流器采取车控模式时,动车组速度vt强制各个轮轴的线速度一致。假设同一车厢4 个轮对的直径分别为D1、D2、D3、D4,且D1>D2>D3>D4,则折算电机转速后有f1 表1 转速、转差率和电机实际功率的关系Tab.1 Relationship between rotating speed,slip and actual power of motor 设计高速动车组牵引电机时需要满足特性差异在±3%以内。当存在轮径差4 mm 时,根据IEC 61377 规定,轮径偏差时的电机转差率smotor为 式中:s 为特性试验中测得的转差率;n 为并联的电动机数;ΔD 为最大轮径差;D 为控制系统设定轮径;+表示牵引运行工况;-表示制动运行工况。 某高速动车组采用车控模式,1 个逆变器模块控制4 台牵引电机。实际牵引系统控制时的速度信号取为4 台电机转速的平均值,因此,轮径偏差4 mm 时,大轮对应电机的影响是+3 mm,电机发挥功率变大,小轮对应电机的影响是-3 mm。 对牵引电机能耗进行仿真建模,在运行过程中,其温升主要取决于损耗。 定子齿损耗PFet为 式中:PFet为定子齿损耗,kW;k1为铁耗校正系数,取k1=3;p50/100为DW465-50 材料硅钢片在1 T、50 Hz 下的损耗系 数,p50/100=2 W/m2;Bt1为定子齿部 磁通密度,T;f 为频率,Hz;Gi为齿的重量,kg。 定子轭损耗PFej为 式中:PFej为定子轭损耗,kW;k2为铁耗校正系数,取k2=2.5;Bj1为定子轭部磁通密度,T;Gj为轭的重量,kg。 定子铁耗PFe为 定子铜耗PCu1为 式中:I1为定子绕组电流,A;R1为换算到基准工作温度的定子绕组电阻,Ω。 转子铜耗PCu2为 式中:I2为转子电流,A;R2为基准工作温度的转子绕组电阻,Ω;Z2为转子槽数;K 为导条系数,K=Z2/m。 牵引电机机械损耗Pfw为 式中:nN为额定转速,r/min;D2为转子外径,mm;PN为电机额定输出功率,kW;jh为0.9~1.3 的经验系数。 牵引电机杂散损耗Ps为 由式(13)~式(17)可以得到总损耗为 根据式(11)和式(18)可以进一步推导出 式中,PsFe为旋转铁耗,表示为 式中,PFei为基本损耗。 为了对不同轮径差牵引电机的发挥功率及温升进行研究,搭建“轮径差-功率温升”仿真模型,具体仿真结果如下。 (1)轮径差0 mm 情况 无轮径差时,按特性曲线控制的电机最大发挥功率及过载能力的仿真结果如表2 所示。平直道不同速度下电机正弦波稳定温升的仿真结果如表3所示。25‰坡道不同速度下电机正弦波稳定温升的仿真结果如表4 所示。 表2 轮径差0 mm 的仿真结果Tab.2 Simulation results with wheel diameter difference of 0 mm 表3 轮径差0 mm 下平直道不同速度下电机正弦波稳定温升Tab.3 Motor sine wave stable temperature rises at different speeds under ramp of 0 with wheel diameter difference of 0 mm 表4 25‰坡道不同速度下电机正弦波稳定温升Tab.4 Motor sine wave stable temperature rises at different speeds under ramp of 25‰ 从无轮径差时不同坡道的数据可以看出,动车组在25 ‰坡道上以200 km/h 的速度运行,温升稳定后铁芯温度将超过预警温度。因此,本次不同轮径偏差的分析不考虑长大坡道工况。 (2)轮径差4 mm 轮径差4 mm 时,按特性曲线控制的电机最大发挥功率及过载能力仿真结果见表5。 从表5 可以看出,电机最大功率为520 kW,出现在车速250 km/h,各速度点过载能力均大于1,过载能力满足要求。 表5 轮径差4 mm 的仿真结果Tab.5 Simulation results with wheel diameter difference of 4 mm 平直道不同速度下,电机正弦波稳定温升仿真结果见表6。 表6 轮径差4 mm 下平直道不同速度下电机正弦波稳定温升Tab.6 Motor sine wave stable temperature rises at different speeds under ramp of 0 with wheel diameter difference of 4 mm 对动车组轮径差4 mm 时平直道上不同速度等级的牵引电机过载能力与温升进行计算,速度等级350 km/h 时电机铁芯超过预警温度,速度等级300 km/h 时电机铁芯存在超温风险。 将表3、表4 和表6 的数据拟合为散点图,如图5 所示,即动车组轮径差0 mm 在平直道、轮径差0 mm 在25‰坡道以及轮径差4 mm 在平直道。从图中可以横向对比不同轮径时在相同速度点下的功率、转差率、绕组温升及铁芯温度的差异。 图5 仿真结果拟合散点Fig.5 Simulation results of scatter fitting 为验证“轮径差-功率温升”仿真模型的结果,搭建滚动台进行试验。对试验车辆匹配不同轮径的轮对,设置滚动试验台特定坡度,并控制牵引变流器使电机达到目标速度,使用监测设备记录该过程中的功率及温升情况。台架试验结果及分析如下。 试验车辆匹配各轴轮对轮径差为0 mm,设置滚动试验台为平直道,控制牵引变流器使电机速度达到245 km/h。该工况下启动阶段、温升稳定后的功率曲线如图6 所示,稳定后测得1 轴电机功率P1为183 kW,3 轴电机功率P3为130 kW,4 轴电机功率P4为120 kW。 图6 工况1 启动阶段、温升稳定后的功率曲线Fig.6 Power curves at the starting stage and after stable temperature rises in working condition 1 该工况下实测电机定子温度曲线如图7 所示,由图可见,4 台牵引电机定子温度上升趋势一致,4轴电机定子实时温度基本相同,当速度上升到245 km/h 时,温度达到最高值,约为90 ℃。 图7 工况1 牵引电机温升实测曲线Fig.7 Measured curves of traction motor temperature rise in working condition 1 试验结果表明,轮径相同时,各轴电机功率发挥和定子实时温度基本一致,与仿真结果相符。 试验车辆匹配各轴轮对轮径差为0 mm,设置滚动试验台为25‰坡道,控制牵引变流器使电机速度达到245 km/h。该工况下启动阶段、温升稳定后的功率曲线如图8 所示,稳定后测得1 轴电机功率P1为442 kW,3 轴电机功率P3为417 kW,4 轴电机功率P4为382 kW。 图8 工况2 启动阶段、温升稳定后的功率曲线Fig.8 Power curves at the starting stage and after stable temperature rises in working condition 2 该工况下实测电机定子温度曲线如图9 所示,由图可见,4 台牵引电机定子温度上升趋势一致,4根轴电机定子实时温度基本相同,当速度上升到245 km/h 时,温度达到最高值,约为105 ℃。 图9 工况2 牵引电机温升实测曲线Fig.9 Measured curves of traction motor temperature rise in working condition 2 试验结果表明,轮径相同时,各轴电机功率发挥和定子实时温度基本一致,与仿真结果相符。与工况1 相比可知,相同速度条件下,25‰坡道比平直道时的电机发挥功率增大,定子温升亦增大。 试验车辆匹配4 轴轮径较其他3 轴大4 mm,设置滚动试验台为25‰坡道,控制牵引变流器使电机速度达到100 km/h。该工况下启动阶段、温升稳定后的功率曲线如图10 所示,稳定后测得1 轴电机功率P1为125 kW,3 轴电机功率P3为127 kW,4 轴电机功率P4为166 kW。 图10 工况3 启动阶段、温升稳定后的功率曲线Fig.10 Power curves at the starting stage and after stable temperature rises in working condition 3 该工况下实测电机定子温度曲线如图11 所示,由图可见,4 台牵引电机定子温度上升趋势一致,但4 轴(大轮径)电机定子温度较其他3 轴温度高约10 ℃,定子温度最大值约为110 ℃。 图11 工况3 牵引电机温升实测曲线Fig.11 Measured curves of traction motor temperature rise in working condition 3 试验结果表明,同一车辆各轴轮对存在轮径差时,轮径最大的轮对对应的电机发挥功率亦最大,定子温度也最高,与仿真结果相符。试验结果统计如表7 所示。 表7 试验结果统计Tab.7 Statistics of test results (1)在不同控制模式下,当高速动车组轮径出现较明显差异,且运行在一些特殊路况时,牵引电机会产生温升差异。随着轮径差的增加,车辆运行的平稳性和稳定性变差,牵引电机功率发挥差异性增大。牵引工况下,大轮径发挥功率较大,容易引起超温风险,轮径差4 mm 情况下会带来40 kW 的功率发挥差异及10 K 左右的温升。制动工况相反,不再赘述。 (2)通过滚动台试验结果与仿真计算结果的对比可以看出,计算结果与试验结果的趋势一致。从不同工况各轴的铁芯温度对比可以看出,各轴电机铁芯温度非常接近,均与轮径差0 mm 时的铁芯温度仿真值相近,而考虑轮径差时的仿真温度与轮径差0 mm 时的仿真温度是存在一定温度差的。 (3)从仿真和试验结果的对比来看,“轮径差-功率温升”仿真模型在具有轮径差动车组牵引电机温升仿真方面有良好的可行性和准确性,该方法可以指导动车组镟修及预测,定量指导健康管理系统逻辑制定和模型优化。

2 仿真建模及其分析
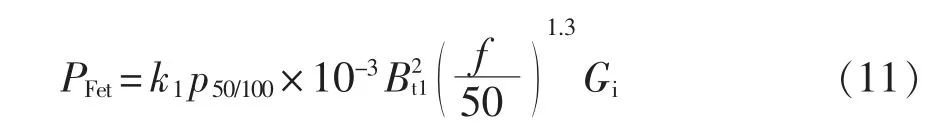
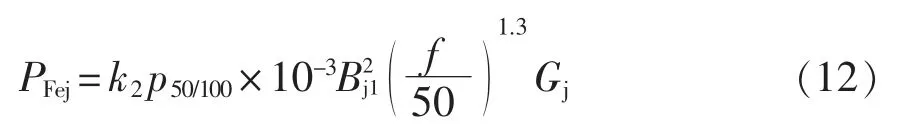



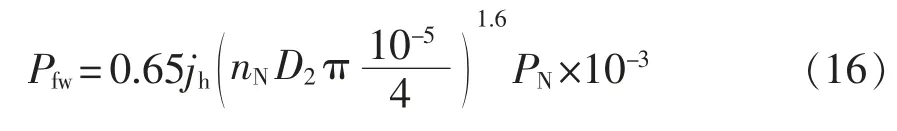

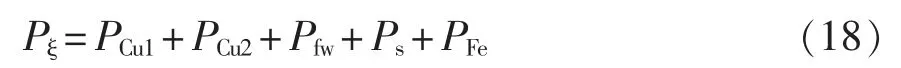
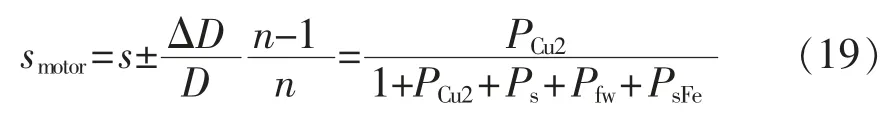
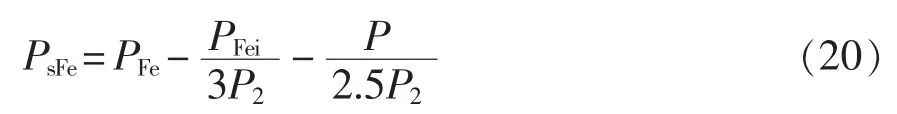
3 试验结果及其分析
3.1 工况1:0 mm、245 km/h、平直道
3.2 工况2:0 mm、245 km/h、25‰坡道
3.3 工况3:4 mm、100 km/h、25‰坡道

4 结论

