基于有源阻尼的大功率永磁牵引电机电流控制

白 龙

（中国铁道科学研究院集团有限公司机车车辆研究所，北京 100081）

牵引传动系统是动车组最重要的子系统之一，目前投入运营的车型采用的大部分是异步电机牵引传动系统。异步电机具有结构简单、可靠性高且成本较低等优点，但需要励磁电流建立磁场，这降低了电机的效率[1-3]。在提倡环保节能的发展背景下，永磁同步电机因其具有高效率和高功率密度的特点，受到了越来越多的关注，而永磁牵引传动系统在列车牵引系统领域也得到了越来越多的应用[4-7]。

国外在轨道交通领域对永磁牵引系统研究较早，德国、日本和法国均已完成了基于永磁牵引系统的动车组和城轨列车的型式试验和考核运用，其中阿尔斯通、庞巴迪和东芝等供应商均获得了一定数量的永磁牵引系统订单，西门子公司也正在就永磁直驱的转向架Syntegra 进行试验研究[8]。国内对列车用永磁牵引系统的研究起步较晚，但近些年来的发展较为迅速。目前由中车时代电气研发的用于城轨车辆的永磁牵引系统已经在长沙1 号线进行了载客运行，而中车四方公司的永磁动车组也已完成型式试验。

传统的永磁电机矢量控制方法已经比较成熟，但应用于大功率列车牵引领域时产生了挑战，其中就有牵引变流器二次谐振回路会引起固定频率点下系统振荡的问题，直接影响了转矩发挥性能和系统稳定性[9-10]。文献[11]提出了取消二次谐振回路后的预测控制方法，较好地解决了系统谐振的问题；文献[12]基于伏秒平衡原则，提出了基于转子磁场定向瞬时改变逆变器频率的无拍频控制方法，较好地解决了转矩脉动问题；文献[13]提出了使用载波移相技术来消除二倍频纹波，从而减小支撑电容大小的方法，但这些控制策略是基于异步电机牵引系统的研究，并未涉及永磁同步电机，而且对于实际工程应用来说，实现起来也较为繁琐；文献[14]针对城轨用牵引变流器稳定性问题进行了研究，分析了中间电容对系统稳定性的影响，但需要修改主电路参数；文献[15]提出了应用于LCL 滤波器的有源阻尼控制方法，抑制了网侧电压电流的振荡，可见有源阻尼的引入是一种可以有效提高系统稳定性的控制方法。

本文将有源阻尼方法应用于大功率永磁同步电机控制中，增加系统阻尼，提高鲁棒性，结合交叉解耦电流控制方法，实现了大功率永磁同步电机电流平稳准确控制，解决了因二次谐振回路的存在导致的固定频率点系统不稳定问题，优化了大功率永磁同步电机应用于列车牵引领域的控制方法。

1 永磁同步电机数学模型

永磁同步电机基于同步旋转d/q 坐标系的电压方程[16]为

式中：ud、uq为定子电压d 轴、q 轴分量；id、iq为定子电流d 轴、q 轴分量；Rs为定子电阻；ωs为同步角速度；Ld、Lq为d 轴、q 轴电感；λf为转子永磁体磁链矢量的幅值。

永磁同步电机的转矩方程为

式中：Te为永磁同步电机电磁转矩；p 为电机极对数。

在实际应用中，永磁牵引电机受到牵引变流器输出能力的制约，电机电流幅值和电压幅值均存在一个极限值，其中电流限幅值设为imax，电压限幅值为umax=2udc/π，udc为直流母线电压。因此，永磁同步电机d/q 轴电流和电压应满足

结合式（1），并忽略电枢电阻，考虑稳态情况，式（4）可表示为

永磁同步电机电流工作点应位于式（3）所示电流极限圆和式（5）所示电压极限椭圆的范围内[17]。

2 永磁同步电机交叉解耦电流控制策略

永磁同步电机在基速以下时，采用最大转矩电流比MTPA（maximum torque per ampere）策略进行控制，由转矩指令和MTPA 公式计算出d/q 轴电流指令，采用交叉解耦控制方法，得到输出电压指令，进而通过调制模块生成PWM 波形。

电流交叉解耦控制方法结构如图1 所示。为了抵消电机定子d/q 轴之间的耦合量，交叉解耦控制在传统id、iq电流控制的基础上，在电机控制矩阵中加入了由电流控制指令组成的解耦项[18]。

图1 交叉解耦电流控制框图Fig.1 Block diagram of cross decoupling current control

补偿的前馈量为

随着电机频率的提高，由电流工作点的式（3）和式（5）可知，输出电压幅值达到极限2udc/π，因此需要采用弱磁控制算法。在弱磁区控制时，d/q 轴电流指令值应满足

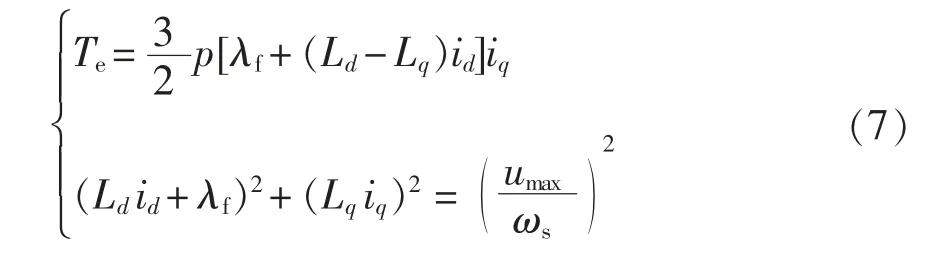
由于输出电压幅值达到极限，电压相角成为了唯一的可控量。在弱磁工况下的电流控制采用单电流环方式，即q 轴电流PI 调节器输出作为电压的相角β，进而得到d/q 轴电压[19]。控制结构如图2 所示。

图2 永磁同步电机控制框图Fig.2 Control block diagram of permanent magnet synchronous motor

非弱磁区的交叉解耦控制和弱磁区的单电流环控制构成了大功率永磁同步电机电流控制策略。永磁同步电机电流工作点曲线如图3 所示。T1、T2为等转矩线，OABC 为电机工作点运行曲线，ABC曲线即为进入弱磁区后的工作点轨迹。

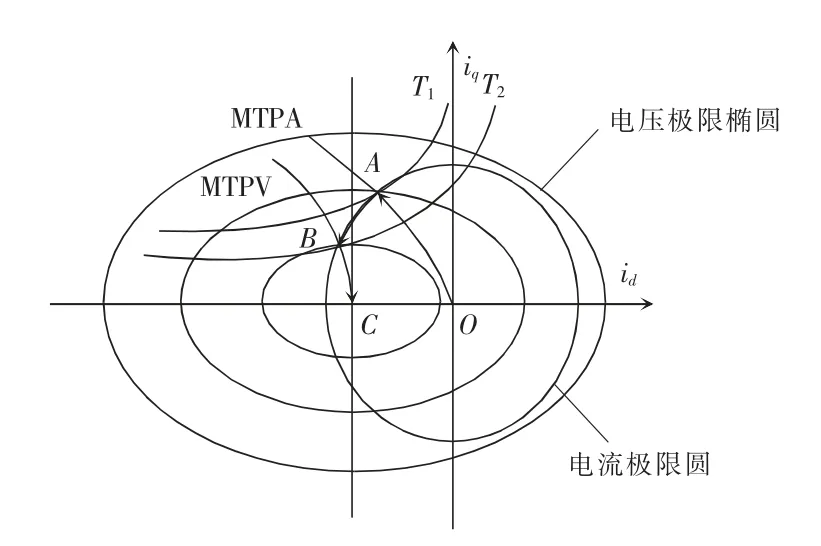
图3 永磁同步电机电流工作点曲线Fig.3 Current working point curves of permanent magnet synchronous motor

3 二次谐振回路对系统稳定性的影响

由四象限整流器工作原理可知，二次谐波电流的存在导致四象限整流器的输出电压上会产生一个二倍于供电频率的交流电压，在系统对直流输出电压要求较高时，需要增加二次谐振回路，让整流器输出的二次谐波电流绝大部分流经该回路，使得直流侧二次交流电压基本为0，二次谐振回路起到二倍频交流短路的作用[10]。

但由于变流器主电路中有支撑电容的存在，和二次谐振回路相结合，会对逆变侧输出造成影响。图4 为包含了支撑电容和二次谐振回路的变流器电路结构。

图4 牵引变流器逆变电路结构Fig.4 Inverter circuit structure of traction converter

考虑中间回路的阻抗特性，中间电容和二次谐振电路并联的输出阻抗为

试验中使用的二次谐振回路L1和C31、中间支持电容C14参数为L1=0.603 mH、C31=4.051 mF、C14=3 mF，代入式（8），计算得到系统谐振频率f0=156.112 Hz。

永磁同步电机与逆变器组成恒功率负载，其输入阻抗呈现负阻抗特性。随着功率的提高或者系统参数的变化，会导致其输入阻抗与中间滤波回路的输出阻抗不匹配，引起系统的振荡。为了便于分析系统特性，建立了带恒功率负载的系统模型，如图5 所示，其中Z 为永磁同步电机与逆变器组成系统的等效阻抗，RL为线路电阻。

图5 带恒功率负载的系统等效模型Fig.5 Equivalent model of system under constant power load

以直流侧电流为输出，直流侧电压输入的系统传递函数为

式（9）为系统的闭环传递函数，其中分母的第二项为开环传递函数G（s），即

Zout如式（8）所示，同时为了便于分析，假设线路电阻RL=1 Ω。而对于电机控制系统输入阻抗Z 的求解较为复杂，文献[5]采用小信号分析方法给出了电流交叉解耦控制下系统输入导纳及输入阻抗，则有

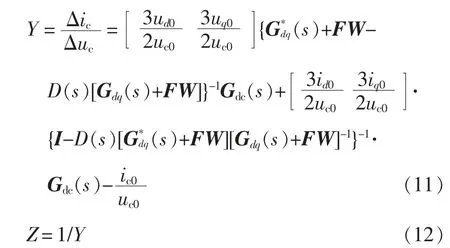
其中

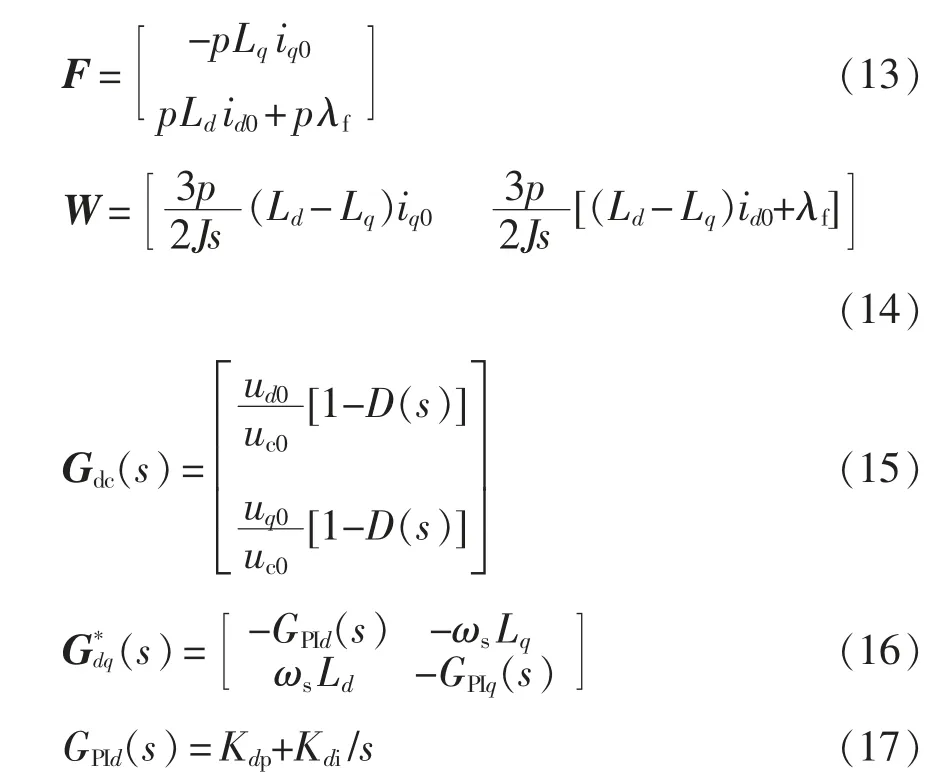
式中：I 为单位矩阵；p 为电机极对数；Ld、Lq为电机d 轴、q 轴电感；ωs为电机角频率；λf为永磁体磁链；J 为电机转动惯量；Kdp、Kdi和Kqp、Kqi为电机d 轴、q轴电流调节器参数；Td为系统的控制延时；ud和uq为系统d 轴、q 轴电压瞬时值；和为系统d 轴、q轴电压指令值；id和iq为系统d 轴、q 轴电流瞬时值；和为系统d 轴、q 轴电流指令值；uc和ic为直流侧逆变器电压和输入电流；ud0、uq0、id0、iq0、uc0、ic0为系统稳态均值。为了方便进行分析，选取系统额定点相关数据，如表1 所示。

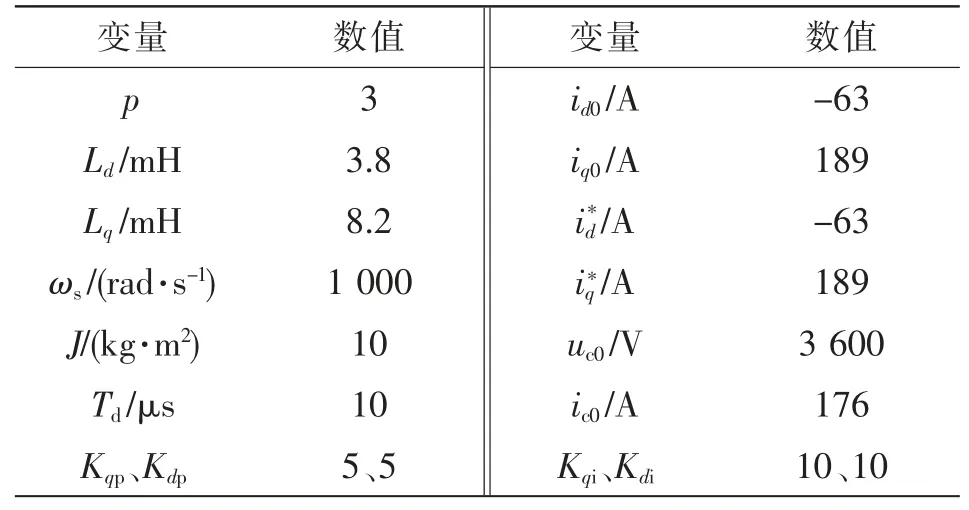
表1 系统额定点数据Tab.1 Data at system rating point

将式（11）代入式（10）中即可得到系统的开环传递函数。代入表1 中数据，绘制开环传递函数的波特图，如图6 所示。

图6 系统波特图Fig.6 Bode diagram of system

由图6 中虚线的标注可以看到，当系统频率为101 Hz 时，系统幅频特性为负值，对于二倍频电压和二次谐波电流起到了抑制作用；当系统频率为157 Hz 时，幅频特性为正，相频特性穿越了180°。开环传递函数波特图判断闭环系统稳定性判据为幅频特性大于0 时，相频特性不穿越（2k+1）π（k=0,±1,±2，…）[5]。由图6 可知，系统处于不稳定状态。

对于逆变侧来说，电机传动系统会在中间直流环节上产生宽频带谐波，各次谐波含量取决于逆变控制的调制算法，低次谐波频率主要是电机定子频率的6 倍频和12 倍频。当逆变器输出频率为nf0（其中f0为谐振频率[14]，n=1，2，3，4，5）左右时，直流侧回路最容易受到谐波激励而振荡起来。对应到本文所研究的永磁控制系统中，当电机频率与系统谐振频率相等（均为157 Hz）时，电机控制系统易发生振荡。

4 有源阻尼方法的引入

为了抑制二次谐振回路引起的逆变侧输出振荡，本文提出了基于有源阻尼方法的新型电流控制策略，即在交叉解耦电流控制的基础上增加有源阻尼补偿项，通过改变系统阻尼系数来抑制振荡，控制结构如图7 所示。

图7 中虚线部分即为增加的有源阻尼项，在永磁同步电机控制中，将有源阻尼系数Ractive与反馈电流id、iq分别相乘，作为负反馈作用到PI 调节器生成的d/q 轴电压。对应到系统导纳模型，则有

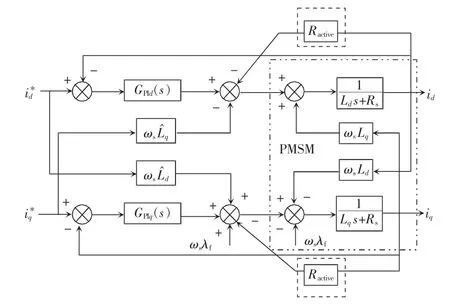
图7 增加了有源阻尼项的电流控制结构Fig.7 Current control structure with active damping term added

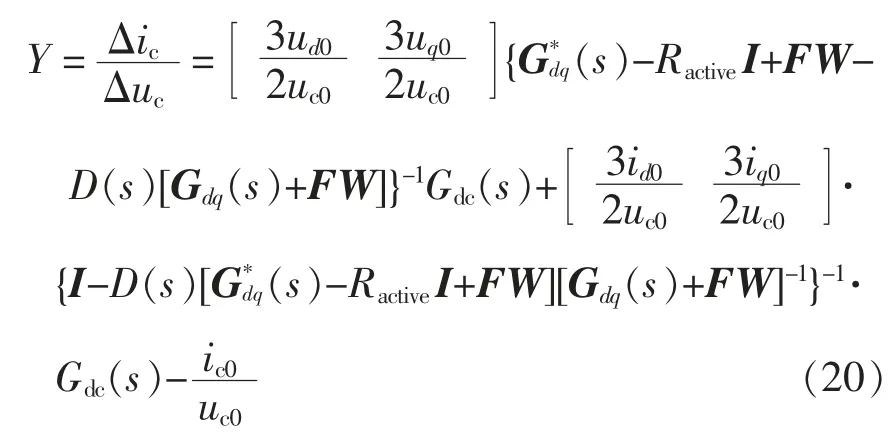
增加了有源阻尼项Ractive的系统波特图如图8所示。由图8（a）可以看到，增加了正有源阻尼项（Ractive=0.8）后，系统频率为157 Hz 时，相频特性没有穿越180°，系统处于稳定状态；未加有源阻尼或者有源阻尼系数为负数时，相频特性穿越180°，系统不稳定。由图8（b）可以看到，有源阻尼较大（Ractive=5）或者较小（Ractive=0.1）不会改善系统稳定性，增大阻尼后反而影响了其他频率点的稳定性。由图8 可知，适当的阻尼系数不会影响其他频率点的稳定性，在实际工程应用中，应根据具体需要调整有源阻尼系数。

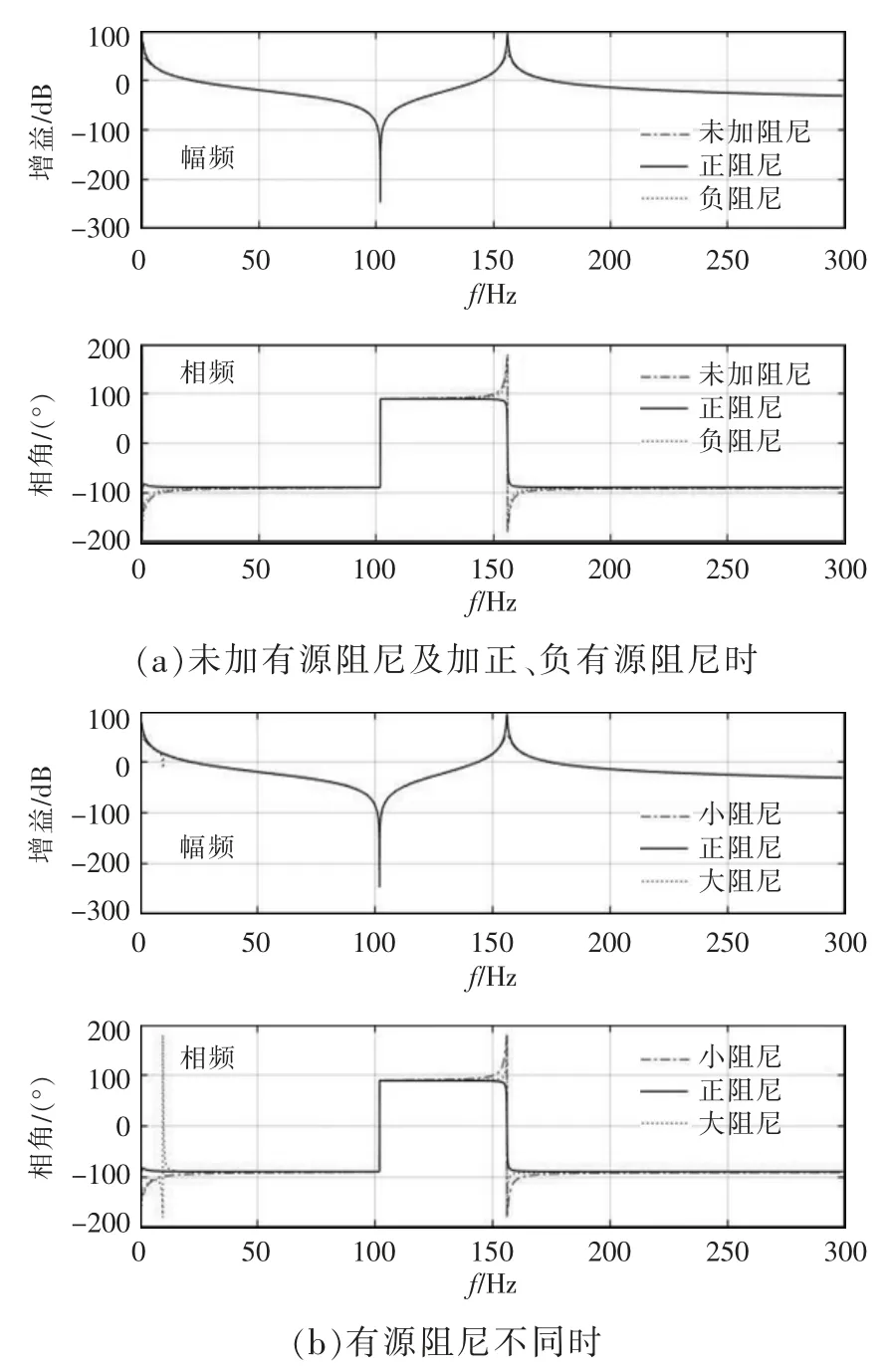
图8 不同有源阻尼下的系统波特图Fig.8 Bode diagram of system with different active damping

由上述分析可知，加入一定的有源阻尼，可以达到抑制谐振、改善系统稳定性的目的。

5 仿真与试验

为进一步验证基于有源阻尼的大功率永磁同步电机电流控制方法的可行性，本文基于600 kW永磁牵引传动系统进行了半实物仿真和地面试验工作。牵引系统交流输入电压为25 kV，四象限整流输出直流电压为3 600 V，采用数字信号处理器DSP28346 实现电机控制算法。

5.1 半实物仿真

基于半实物仿真平台搭建了永磁牵引传动系统，采用实际的动车组用牵引控制单元TCU 实现电机控制算法以及传感器信号反馈等功能，得到半实物仿真结果如图9 所示。

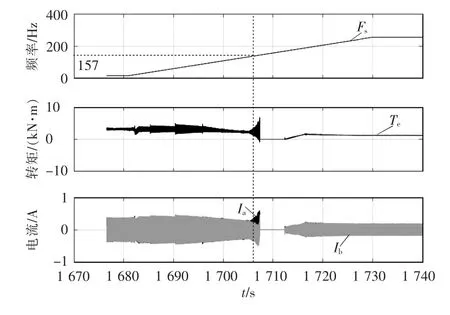
图9 谐振时的半实物仿真波形Fig.9 Hardware in the loop simulation waveforms with resonance

由图9 所示的半实物仿真波形可以得到，当进入到特定频率段即定子频率为157 Hz 时，电机的转矩、电流以及直流侧电压均开始振荡，并有发散趋势，过流后系统封脉冲保护。特定频率157 Hz 与理论分析一致，为系统的谐振点。

在加入有源阻尼项后，仿真波形如图10 所示，系统振荡得到了明显抑制，全速度范围内转矩发挥平稳，可见有源阻尼起到了改善系统稳定性的作用。

图10 增加有源阻尼后的半实物仿真波形Fig.10 Hardware in the loop simulation waveforms after adding active damping

5.2 地面试验

采用实际动车组用牵引变流器机组，对一台600 kW 永磁同步电机进行地面试验，结果如图11所示，图中波形从上到下依次为电机的相电流、相电压、转速以及转矩等。

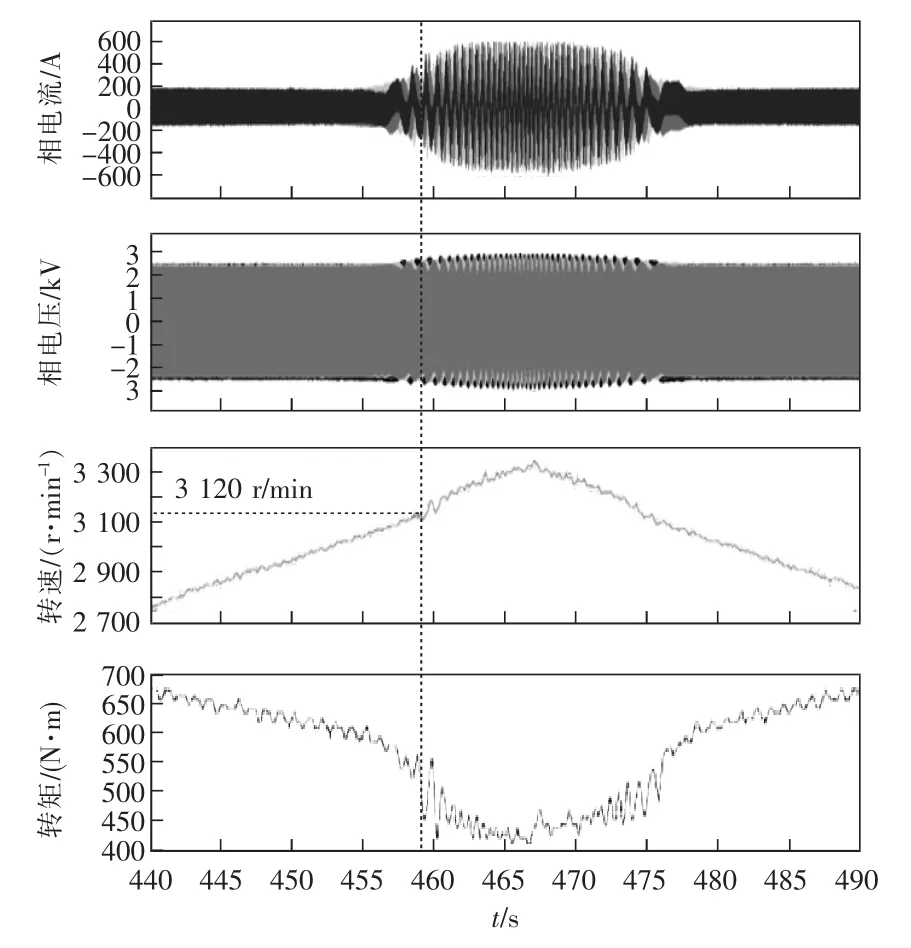
图11 谐振时的地面试验波形Fig.11 Ground test waveforms with resonance

5.2.1 未加有源阻尼的试验

未加有源阻尼，对永磁同步电机进行满转矩全速度扫描试验。由图11 中虚线可以看到，在定子转速为3 120 r/min（定子频率为156 Hz）附近时，电机定子电流、电压、转矩均出现了振荡。电流最大振荡幅值到达600 A 后，转矩出现±100 N•m 的持续波动，紧急降转矩避免电流和转矩冲击过大。选取振荡时的相电流进行频谱分析，结果如图12 所示。可见，除定子频率为156 Hz 外，在低频段（1～5 Hz）存在较大的分量，系统低频振荡严重。

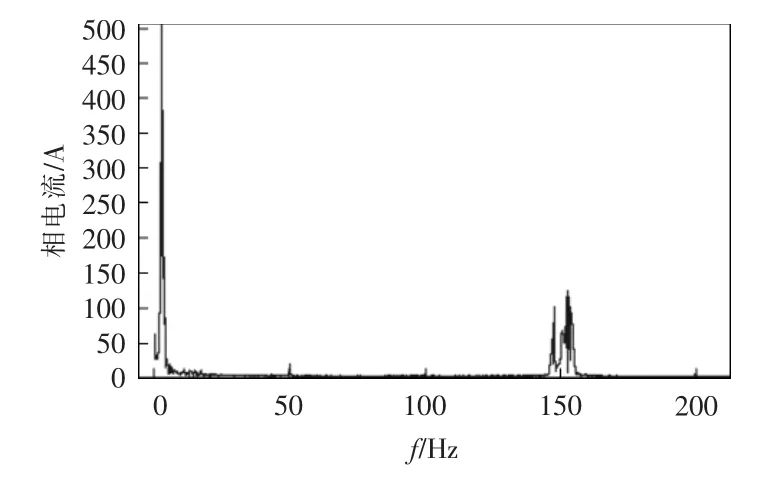
图12 未加有源阻尼的相电流频谱Fig.12 Phase current spectrum without active damping

5.2.2 增加有源阻尼后的试验

增加有源阻尼项且有源阻尼系数为0.7 时，速度扫描试验波形如图13 所示，转矩发挥平稳，电压和电流的振荡消失。图14 为相电流频谱，低频（1～5 Hz）分量得到了明显抑制。可见有源阻尼改善了系统的稳定性。

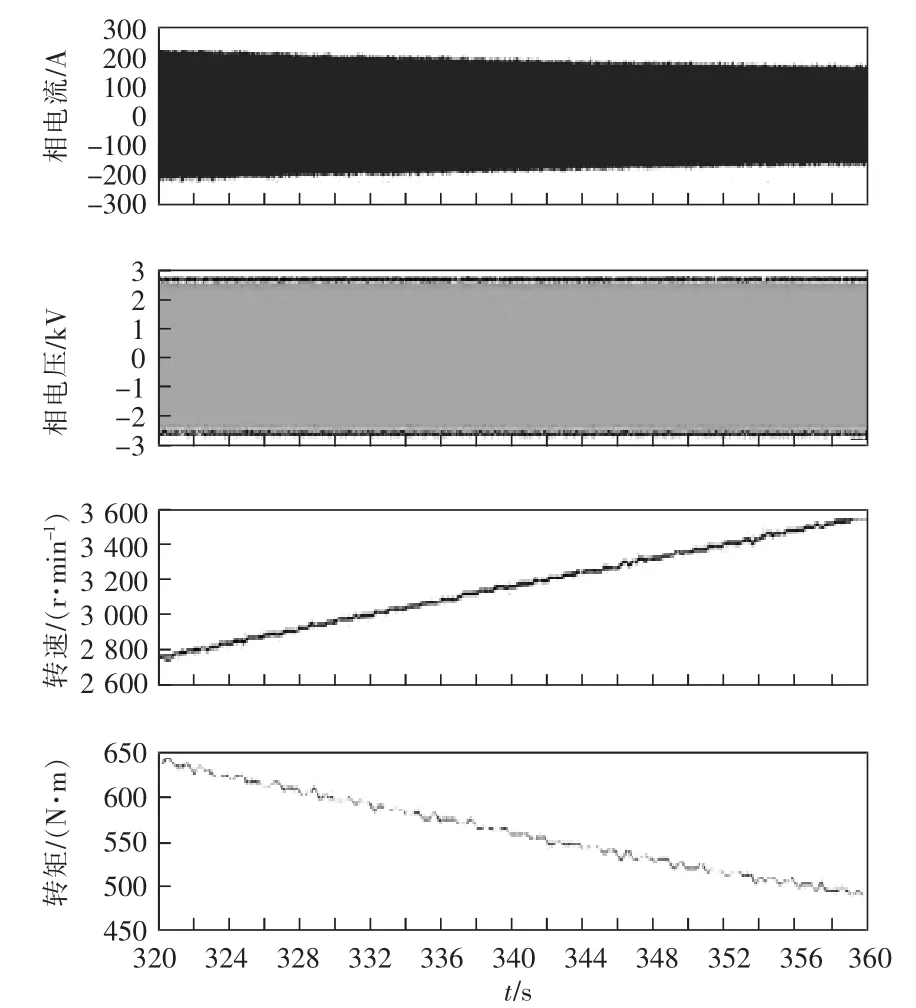
图13 有源阻尼系数为0.7 的地面试验波形Fig.13 Ground test waveforms with active damping coefficient of 0.7

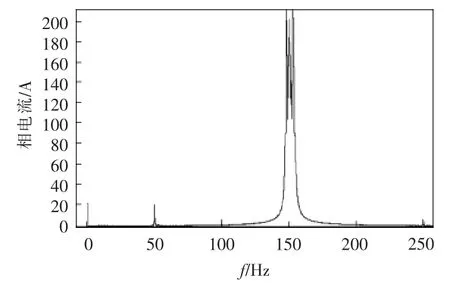
图14 加有源阻尼的相电流频谱Fig.14 Phase current spectrum with active damping

6 结语

本文旨在对永磁同步电机应用于大功率列车牵引领域时的控制算法进行优化，针对二次侧谐振回路影响固定频率处系统稳定性的问题，提出了基于有源阻尼方法的交叉解耦电流控制策略，通过增加一定程度的系统阻尼，消除了因谐振引起的电机转矩、电压以及电流振荡问题，提高了系统的鲁棒性。通过600 kW 永磁同步电机的半实物仿真和地面机组试验验证了该方法的可行性。