一道得分很低的高考概率题引发的思考

蔡海涛 卢 妮 卓晓萍

(福建省莆田第二中学 351131)

2020年的高考已落下帷幕，一道道赏心悦目的高考试题让人回味无穷.其中，全国卷Ⅰ理科第19题得分率很低.据某省高考评卷点统计，该题得分为所有解答题中得分最低，比第21题的函数导数压轴题还低.笔者访谈部分考生，这道题能够完整作答的寥寥无几，这一现象引发笔者的思考.

一、试题呈现

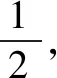
(1)求甲连胜四场的概率；

(2)求需要进行第五场比赛的概率；

(3)求丙最终获胜的概率.

二、试题分析

本题以三人的羽毛球比赛为载体，考查概率中事件的概念、事件的独立性和事件概率的计算等基础知识，考查推理论证能力、运算求解能力和应用意识，考查分类与整合、统计与概率数学思想，考查逻辑推理、数学建模等核心素养，体现基础性、应用性和创新性.

第(1)问根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率，这一问比较简单，大部分考生都能轻松求解.低起点的第一步有利于稳定考生的心态，更有信心去解决后续的问题；第(2)问计算出四局以内结束比赛的概率，然后利用对立事件的概率公式可求得所求事件的概率；第(3)问列举出甲赢的基本事件，结合独立事件的概率乘法公式计算出甲赢的概率，由对称性可知乙赢的概率和甲赢的概率相等，再利用对立事件的概率可求得丙赢的概率.本题第(2)、(3)问易错点在于对基本事件考虑问题不清、分类标准不明.解题关键在于先分析题意，理解比赛规则，合理确定分类讨论标准.

三、解法分析

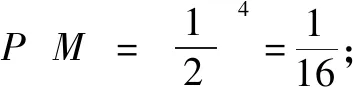
(2)记事件A为甲输，事件B为乙输，事件C为丙输，则四局内结束比赛的概率为

P′=P(ABAB)+P(ACAC)+P(BCBC)+P(BABA)

(3)记事件A为甲输，事件B为乙输，事件C为丙输，

记事件M:甲赢，记事件N:丙赢，则甲赢的基本事件包括：BCBC、ABCBC、ACBCB、BABCC、BACBC、BCACB、BCABC、BCBAC，

所以，甲赢概率为

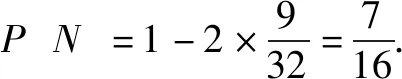
评注这个解答是官方提供的唯一解答，简捷明了，但由某省高考评卷点反馈，第(2)问、第(3)问能够这样解答的考生寥寥无几.这种解答的关键是准确列举出符合条件的基本事件，这要求考生能合理抽象数学模型，合理利用文字语言与符号语言或图形语言之间的转化，分析基本事件的类型，做到不重不漏，考查考生分类与整合的数学思想.

解法二(1)同解法一.

(2)需要进行第五场比赛，即胜者必然要输一场.

于是先考虑对立事件：最终胜者全胜分三类(注意到甲、乙具有对称性)

最终甲胜按输者排序：乙丙乙丙；最终乙胜按输者排序：甲丙甲丙；

最终丙胜按输者排序：甲乙甲乙；乙甲乙甲.

四场结束比赛的概率为：

故进行第五场比赛的概率为

(3)丙获胜情况分为两类:比赛场次4场或5场.

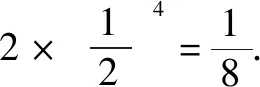
情况二：比赛5场，则丙输一场(注意到甲、乙具有对称性，先考虑第一场甲赢)

第二场输按输者排序：

乙丙甲乙甲；乙丙乙甲甲；

第三场输按输者排序：

乙甲丙乙甲；乙甲丙甲乙；

第四场输按输者排序：

乙甲乙丙甲

评注解法二是利用列举法列举出符合条件的基本事件.求古典概型的概率很重要的一步是列举基本事件，对于一些情况比较复杂、数据较大时，“列举”稍有疏忽，就会出现遗漏.列举法的关键在于如何确定分类讨论的标准，由此揭示基本事件的构成规律，若能抓住这个规律列举就不难了.如第(2)问、(3)问分别以“最终胜者全胜”、“丙获胜情况”做为分类讨论标准.

解法三根据失败者的特点,可列出每场失败者的情况如下表:

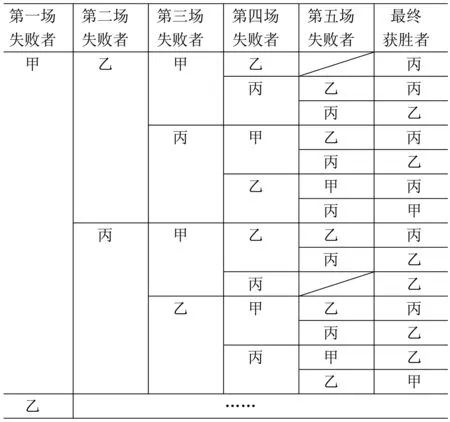
根据上表解答本题如下：

(2)只需进行四场比赛的概率为:

所以需要进行第五场比赛的概率为

(3)比赛四场结束且丙最终获胜的概率为

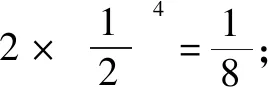
评注解法三首先分析题意，理解比赛规则.由规则知至少需要进行四场比赛，至多需要进行五场比赛，每场比赛失败者的情况有如下特点：首场比赛失败者是甲或乙；前四场比赛不出现连续两场比赛是同一个失败者；若仅进行四场比赛就决出最终获胜者,则两个失败者必是交替失败的.考生若能分析以上特点，则可列出每场失败者，从而掌握比赛可能出现的情况，进而解决问题.

四、教学启示

1.似曾相识燕归来

由于题1得分很低，笔者关注此类试题，发现近年高考出现类似试题，如：

(2019年高考全国卷Ⅱ·理19)11分制乒乓球比赛，每赢一球得1分，当某局打成10∶10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束.甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立.在某局双方10∶10平后，甲先发球，两人又打了X个球该局比赛结束.

(1)求P(X=2)；

(2)求事件“X=4且甲获胜”的概率.

由此，不难发现近年高考数学卷多次设计以体育运动为问题情境的试题，体现了高考积极的育人导向作用，传达着“野蛮其体魄，文明其精神”的体育意识，充分落实“五育并举”的精神.

2.咬定青山不放松

纵观近五年(2015年-2019年)全国卷Ⅰ理科卷概率统计解答题，均是概率与统计相结合，各地的高三质检卷、模拟卷在概率题考查上大都也是以这种形式呈现，考生在应试时发现试题不是平时的套题，从而造成紧张畏难情绪，因此得分较低.当前高考力求创新，落实了从“能力立意”到“素养导向”的转变，考查了考生的数学素养.这就给那些高三复习搞“忽视教材、追踪热点、题海战术”备考策略的教师敲响了警钟，启示我们在高考备考时要稳扎稳打，关注过程性教学，在思想的高度上去引领方法，去领会、感悟分析问题和解决问题的能力.

我们认为每一个知识板块都有可能成为“压轴题”的载体，所以在复习备考时，我们反对“猜题押宝”，只有夯实基础，理清知识体系，提升学生能力，才能应对强调创新的新高考，才能做到以不变应万变，笑傲考场.

3.不畏浮云遮望眼

“中国高考评价体系”明确指出：高考考查要求应体现“基础性、综合性、应用性、创新性.”概率问题联系十分广泛，来源于实际，又服务于实际生活，因此在高考试卷中常承担着考查考生应用数学知识解决实际问题能力的角色.近几年的高考概率统计题中，愈发明显的突出理论联系实际的导向.考生答题过程中，普遍感觉困难，原因在于读不懂题目，不熟悉题目背景，缺乏语言转换能力，不了解概率统计等基本概念的实际意义.

因此，教师要引导学生注重题意分析，提高数学阅读分析能力，把好“读、审、析”三关.即“读”：文字信息，图表信息，初步了解考查的知识点；“审”：结合考查目标，理解图文的内在含义；析：整合有效信息，理清数据关系.还有，教师要关注生活背景、社会现实、经济建设、科技发展等多个方面，从中提炼出具有社会价值的数学应用背景，注重培养学生善于从普通语言中捕捉信息、将普通语言转化为数学语言的能力，使学生能以数学语言为工具进行数学思维与数学交流，再利用有关的数学知识加以解决.还有，由题1的三种解法可以发现解法三简单明了，学生通俗易懂，可见构建表格可以将复杂问题简单化，便于发现问题的规律，列出基本事件的可能情况.“文不如列、列不如表”，表格既具有图形语言的直观性，又兼有符号语言的简洁性，更具有文字语言的通俗性.因此，借助构建表格，剖析结构特征，使问题迎刃而解.