以退为进——刍议高中数学函数解题技巧

唐 艳

(四川省德阳中学校 618000)

随着人们对教育质量的要求逐渐提高，越来越重视对学生能力的培养.高中是学生在整个学习生涯中的一个重要的阶段，在高中的教学过程中，教师不应该仅仅是教授学生书本上的知识，而是应该从书本的内容出发，教授学生更多的数学思想和解题技巧.只有这样，才能以不变应万变，应对高中生涯中源源不断的各种试题，才能更加有效地提高学生的数学成绩.以退为进是一种基本的数学思想，在高中数学函数解题的教学过程中，以退为进数学思想的运用被人们所热议.基于此，对以退为进在高中数学函数解题中的探析势在必行.

一、函数的含义

在中国，函数一词是清代数学家李善兰最初使用的.他在1859年与英国学者烈亚力合译的《代数学》一书中，将“function”译作“函数”.函，即“信”，李善兰老先生巧妙的用寄信来比喻函数，就是为了方便后来学习的人能够轻易理解函数的意义.“你写一封信”就是“一个自变量x”，“你写的所有的信”构成了集合为“值域{f(x)|x∈A}(⊆B)”，“你的朋友圈里的所有人”构成的集合就是“集合B”.顺着这个比喻往下理解，就很容易理解“使对于集合中的任意一个x， 在集合中都有唯一一个确定的数f(x)和它对应”这句话了，就是说信x只能有一个收信人y，即f(x)， 不可能一封信有多个收信地址；而一个收信人却可以收到很多信，即一个x只能对应一个y，而一个y却能有多个x与之相对应.

二、以退为进在高中数学函数解题中运用的意义

思维是开启智慧的钥匙，是开拓者手中的拐杖.以退为进，是我国数学教育的重要思想，是教师进行有效教学的重要策略和手段，是对我国原有数学教育思想和教育方法的重要改革，是践行高中数学新课程改革标准的具体措施.以退为进在高中数学函数解题中的运用是新时代下新课改的要求，也是社会对新时代人才的要求.以退为进，就是从抽象退到具体，从复杂退到简单，从整体退到部分，总之，退到一个能够解决问题的地方.

以退为进在高中数学函数解题中的运用为教师的实际教学指明方向，优化了教师的教学过程，提高了学生对函数知识的吸收能力，提高了教师对学生的函数教学质量和函数教学的实效性，有利于树立学生对于函数学习的自信心，加强其面对问题积极应对的决心，让学生具备一定的逻辑思维能力和自主探究能力，使学生能够充分的理解函数、掌握函数学习的基本定理和规律，让学生们能够熟练地运用所学的函数知识解决生活中的各项难题，让高中数学的教学事半功倍，对于学生、教师、乃至社会意义重大.

三、以退为进在高中数学函数解题中的运用策略

1.以退为进解填空题

退中有法，以退为进，退出了一些选择题、填空题的解题技巧，看似旁门左道，却节省时间，提高效率.以退为进在高中数学函数解题中的运用的第一个“退”就是退到特殊情况，这里的特殊情况包括：变量值的特殊化、函数解析式的特殊化、图形形状的特殊化、位置关系的特殊化、极端化也是一种特殊化、甚至还包括定量问题特殊成定性问题等等.由这些退到以上这些特殊情况，就产生了“特殊值法、特殊函数法、特殊图形法、极端分析法、估算法”等由以退为进而产生的解题策略.通过这些方法用来解决高中数学函数的选择、填空题是十分有效的，这些方法正是体现了——退中有术，实现了以退为进在高中数学函数解题中的巧妙解决方法.

A.11 B.10 C.9 D.8

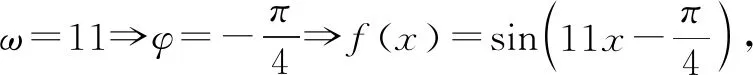
2.以退为进解综合题

很多学生对于解答数学综合题往往感到无从下手,而在高考数学中,综合题占了半壁江山.因此高考数学考得是否成功,很大程度上取决于综合题.数学综合题各个知识点之间是互相补充、制约和渗透的,考查考生对基本知识点的掌握、理解及运用，综合题的题设条件内涵丰富,对解题过程中的转化、变换、联想、类比、归纳等技巧要求高,题目的结论还可以是开放性的,主要考查考生思维的发散性和独创性,这些都是高考的热点.在函数解题的过程中，教师要在实际的高中数学教学活动时，充分发挥学生们的发散思维.教师可以利用书本中的例题来对某一知识点进行反复论证与讲解，尽可能的融合书里的知识，抓住学生数学学习的盲点及误区，培养学生多方面的解题思路，让学生能更好地学习和吸收数学知识.

3.以退为进看题目

“看懂题目”简单的说就是审题，审题说起来简单，真正做起来大多数人可以做到，但是能够正确审题的学生却少之又少.在高中函数的解题过程中，很多学生都会在解题过程中出现各种各样的错误，其原因很多都是因为审题的时候出现了失误.在审题过程中，要求学生能都清楚的了解题目的题意，清楚明白命题的层次结构及其隐藏条件，这样才能解出题目的正确答案.所以，教师教授高中数学函数解题技巧时，要注意培养学生的审题能力，用以退为进的方式让学生能看懂题目，让学生先退到学生最容易看清楚的地方，认透了，钻深了，然后再上去.引导学生能够独立自主的发现题目中的隐含条件，使学生掌握解题的基本方法，进行正确的解题，培养学生的韧性和毅力.让学生从“完全不认识”到“担心害怕”到“壮着胆子试试”，从“慢慢认识”到“找到规律”到“得出正确结果”.在遇到一个很困难的问题时，可将它们分解为一系列的步骤.

例如，已知f(θ)=sin2θ+sin2(θ+α)+sin2(θ+β)，其中α,β是满足0≤α≤β≤π的常数，试问α,β为何值时，f(θ)与θ无关.分析:根据题设条件可知，对于所有不同的θ，f(θ)恒为定值.为了探求α,β的值，所以我们考虑θ的几个特殊值，θ=0,-α,-β，使f(θ)的表达式变得较为简单.

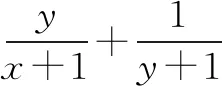
以退为进就是给学生设置问题串,把比较复杂的题目通过问题串的形式一步一步退到最基础的题目上来,发现题目想考查的知识点,让学生更能理解出题者的意图.

综上所述，以退为进在高中数学函数教学中的应用和渗透至关重要，新时代下对高中数学的教学，应该致力于将以退为进应用于高中数学函数的教学中，用以退为进的方式解填空题、综合题，用以退为进的方式让学生看懂题目，教师在教学中要积极进行以退为进教学方式的提炼和渗透，加强对以退为进的应用，这样才能实现学生的自我完善以及综合能力的提高，促进我国高中数学的教学水平和教学质量的提高，为社会和国家培养出优秀的社会主义接班人.