以数学建模素养的培养促进高中生数学核心素养的发展

马志强

(广东省番禺中学 511489)

一、数学建模的定义

数学建模素养是指对实际问题进行抽象概括，然后用数学语言表述问题，最终用数学方法实现构建模型来解决这类问题的素养.它的主要步骤包括：1.从数学的角度发现并提出问题；2.以数学的方法分析问题并建立解题模型；3.从模型中确定所需的参数并计算求解；4.将计算结果代入实际问题进行检验并找出不足；5.改进并完善模型后用来解决实际问题．

二、数学建模的重要性

1.新课标中的体现

在旧的课程标准中，侧重于对数学能力的表述,在旧的课程标准中提出了数学的五大基本能力：“抽象概括、空间想像、推理论证、运算求解和数据处理”，更多的是要求学生理解和掌握数学知识.在《普通高中数学课程标准》(2017年版2020年修订)中在能力与素养上与旧课标有着一定程度上的相同表述,表现出对数学学科五大能力新的解析和新的要求.新课标着重强调了数学的学以致用，尤其是新课标中在数学核心素养中新增加了数学建模素养, 强调要将数学知识应用于实际生活中, 用来解决在实际生产生活中遇到的问题.这一改动并不是突然的, 而是水到渠成的，因为数学建模能够提高学生的数学知识的应用能力并能够培养和发展学生的创新能力, 让学生真正体会将理论用于实际, 感悟数学的实际价值，提高学习数学的兴趣与意识.在数学建模的过程中还需要用到其它的数学核心素养，由此可见数学建模在之后的数学教育中的重要性会日益凸显,必将会得到更进一步的重视与发展.

2.高考指挥棒的体现

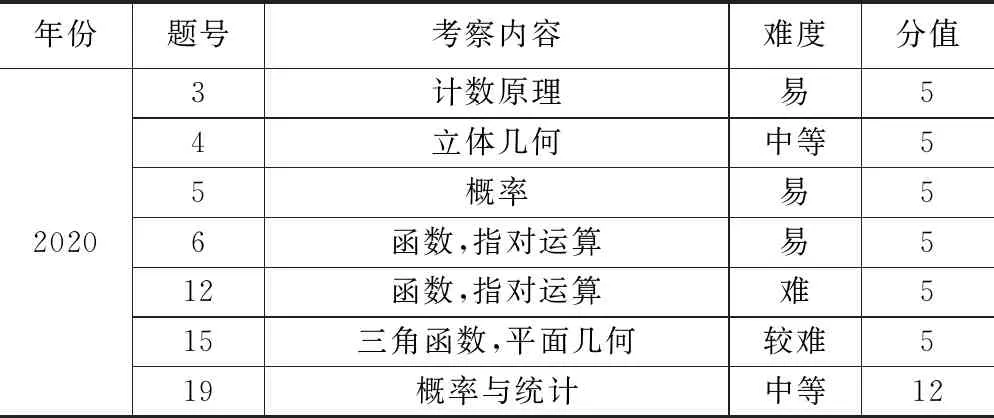
笔者收集和整理了2020年前的高考试题(以全国高考Ⅰ卷为例)数学建模试题与2020高考数学试题(以新课标全国高考Ⅰ卷数学(山东卷)为例)的比较(分值比重，考察范围，题型变化等)，如下表：

2020年新课程全国高考Ⅰ卷数学(山东卷)

从以上表格中可看出：1.高考中数学建模的题型涉及函数，数列，计数原理与排列组合，平面几何与立体几何，三角函数，概率统计，线性规划等，涉及高中数学知识的各个方面，其中概率统计，计数原理与排列组合为高频考题.2.考察知识可分为两大类：(1)直接去联系数学知识和数学工具来解决实际问题；(2)先将实际问题(文字语言信息)进行数学化(用图形语言、符号语言进行描述、解释)，再联系数学中的工具去解答，后将得到的结果(或结论)去回答实际问题.3.难度以中等偏易为主，少数难度较高题型.4.所占分值比重越来越大，16-17年均为22分，18-19年均为27分，而2020年是创纪录的42分，且知识点分布更广！

从历年高考题数学建模题型的题量与分值变化可以看出，今后在高考中数学建模题型将越来越受重视，所占比重也会越来越高，这就要求教师在平时的教学中要充分培养学生的数学建模能力，让学生真正将理论运用于实际，用数学解决实际的生活问题.

三、普通高中生数学建模能力的评价

1.在《普通高中数学课程标准》(2017年版2020年修订)的附录1中，数学核心素养之一的数学建模的水平被划分为三个水平，喻平教授把这三种水平更形象地划分为知识理解(水平一)、知识迁移(水平二)、知识创新(水平三).

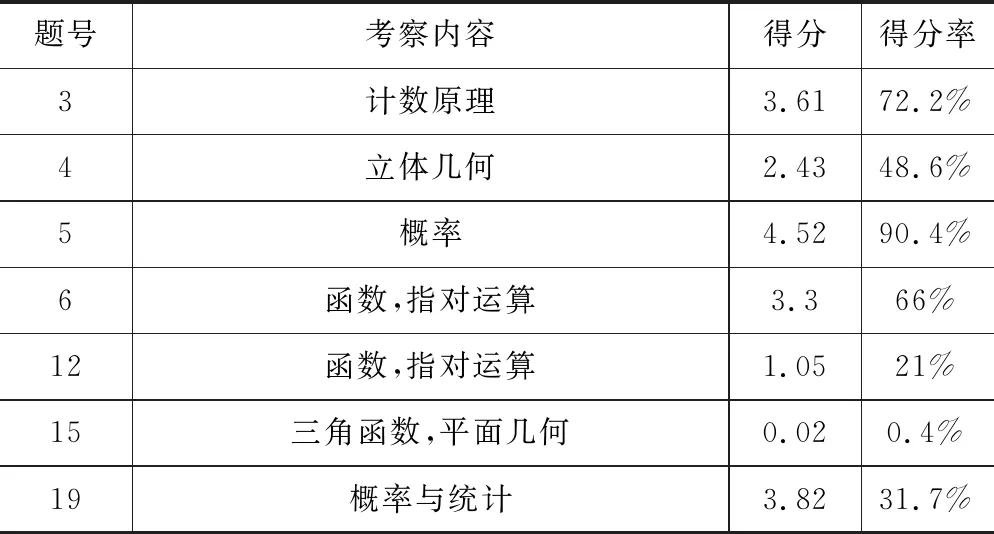
2.以下表格是2021届高三部分学生(笔者任教的学校)完成2020年高考试题(新课程全国高考Ⅰ卷数学(山东卷))数学建模试题的得分情况，能部分体现现在普通高中生数学建模的水平：

题号考察内容得分得分率3计数原理3.6172.2%4立体几何2.4348.6%5概率4.5290.4%6函数,指对运算3.366%12函数,指对运算1.0521%15三角函数,平面几何0.020.4%19概率与统计3.8231.7%

从上方表格中可以发现学生对于直接去联系数学知识和数学工具来解决实际问题的试题得分率较高，但先将实际问题进行数学抽象，再联系数学中的工具去解答的试题得分率是偏低的.试后通过对部分学生的调查了解发现主要有以下问题：(1)看不懂题目，只能瞎猜如第12题(阅读理解差)；(2)不会转化为数学模型如第4题(抽象能力差)；(3)运算出错如第6题(计算能力差)；(4)不会整理和使用已知数据，如第19题(数据分析能力差).

普通高中生数学建模现状主要体现为：(1)学生们对于老师在课堂上介绍和展示的数学建模范例有很大的兴趣，觉得很有趣并体会到了数学知识在实际生活中的巨大用途，这非常有利于数学建模教学活动的开展与实施.(2)学生的阅读理解、抽象概括能力还有待提高.很多学生不会从实际问题中抽象出问题的本质，并简化为数学问题.如何用数学语言表述现实问题是学生数学建模的一大难点.学生需要学会把实际问题转化为数学问题，也需要将用数学模型得到的结论用通常语言来表述，在教学实践中学生们往往并不能很顺利的转化，特别是一些较复杂的问题.(3)学生的个体差异，需要进行合理分组.在实际的教学中，学生的个体差异非常的明显，有些同学理解的很快，而有些同学面对这些问题难以下手，需要较多的时间去领会.

以上各方面都能体现出现阶段高中生数学建模的水平都还是处于比较初级的阶段，在情境中建立数学模型还有一定的困难.

四、对高中生数学建模能力培养的启示

1.教师要提高自身的建模意识，转变教学方式

传统教师大部分只是单纯的传授数学知识，较少注意数学的应用；学生感觉数学很抽象，难以理解，而且没有什么用处，渐渐对数学的学习兴趣大幅降低.因此教师应转变自身的教学方式，从应用的角度出发，利用多媒体手段，在不同阶段提供不同数学应用的实际背景，让学生切身体会数学的实际应用，逐步理解并学会利用数学建模的思想去解决现实的问题.

2.高中数学其它核心素养在数学建模素养中的渗透

在数学建模的过程中，学生同时需要使用其它的数学知识，这就为学生提供了努力学习数学知识的动力，促进其它数学素养的提高，而其它数学素养的提高又会进一步促进数学建模素养的提高.

重视培养学生数学建模的能力已成为数学教育界的共识，在数学建模的教学活动中，在学生解决建模试题的过程中，在研究性学习的活动中，学生在老师的指导下，需要不断的使用数学抽象，逻辑推理，直观想象，数学运算和数据分析等数学知识，方法，这样学生的数学应用意识会越来越强，数学水平也能逐步的提高.可以看到在数学建模的过程中，高中数学的六大核心素养是渗透在其中的，可以说要提高学生的数学素养，数学建模素养的培养是关键，数学建模素养的提高能有效促进高中生数学核心素养的发展.