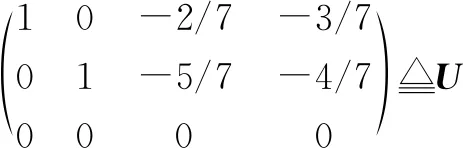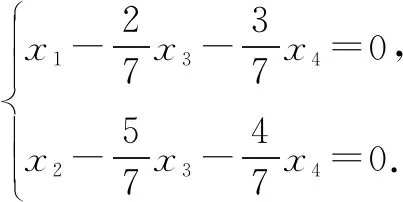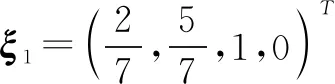关于利用初等变换法求解线性方程组的教学研究与探讨

夏远梅

(重庆师范大学数学科学学院 401331)

在《线性代数》的教学中，初等变换法是一类非常重要的方法，同时也是学生在利用初等变换法求解线性方程组过程中容易混淆的一类方法.学生之所以在利用初等变换法求解线性方程组过程中容易混淆，其根本原因是初等变换法包括初等行变换和初等列变换两类方法，学生在利用初等变换法求解线性方程组过程中容易将两种变换法混合使用并且我们在课堂教学中往往只讲了初等行变换求解线性方程组的方法，导致学生对初等列变换求解线性方程组的方法的掌握总是懵懵懂懂，所以容易产生混淆.本文通过对两类方法进行介绍并解释为什么需要这样进行分类，通过让学生着手练习，建议学生采用初等行变换求解线性方程组的方法，使得学生熟练掌握利用初等变换法求解线性方程组并避免在求解过程中混淆使用.进一步，采用线上线下相结合的教学模式，利用雨课堂让学生线上提交答案，掌握学生的学习与收获情况，并根据学生掌握的情况对相应的知识内容进行补充.下面首先回顾一下什么叫初等行变换、初等列变换和初等变换：

定义1 下面三类变换称为矩阵的初等行变换：

(1)对换变换：将矩阵的某两行对换位置(对换i，j两行，记作ri↔rj)；

(2)倍乘变换：以非零常数k乘矩阵某一行的各元(第i行乘k，记作ri×k)；

(3)倍加变换：将某一行所有的元素的k倍加到另一行对应的元素上去(第j行的k倍加到第i行上，记作ri+rj×k).

把定义中的“行”变成“列”，即得矩阵的初等列变换的定义(所用记号是将“r”变成“c”).矩阵的初等行变换和初等列变换统称为矩阵的初等变换.

考虑如下线性方程组：

其矩阵形式是Ax=b.当b=0时，就是齐次线性方程组Ax=0.利用初等变换法求解上述线性方程，也就是对其增广矩阵做初等变换，主要包括两类：

利用高斯消元法对线性方程组进行消元的过程，针对的是方程与方程之间的运算，也就是相同未知量的系数之间在进行运算，而不是不同未知量的系数在进行运算.因此，利用初等变换法求解线性方程组需要注意：

(1)由于增广矩阵(A,b)的第i列(1≤i≤n)对应的是线性方程组xi的系数，第n+1列对应的是线性方程组的常数项，利用高斯消元法对线性方程组进行消元的过程对应的也就是对(A,b)做初等行变换，故只能对(A,b)做初等行变换.

无锡阳山地区历史上就文化鼎盛，地域特征明显。阳山不仅是历史名镇、旅游名镇，更应该是文化名镇。阳山拥有悠久的历史，有着丰富的自然资源，是吴文化的发祥地和重要源头之一。现如今，在阳山镇党委和政府的带领下进行进一步的深化改革，坚持走中国特色的社会主义道路，落实科学发展观，进一步弘扬阳山独有的文化。

(2) 同样地，由于增广矩阵的转置(A,b)T的第i行(1≤i≤n)对应的是线性方程组xi的系数，第n+1行对应的是线性方程组的常数项，利用高斯消元法对线性方程组进行消元的过程对应的也就是对(A,b)T做初等列变换，故只能对(A,b)T做初等列变换.

在利用初等变换法求解线性方程组时还常涉及两个重要定理，用于判别线性方程组有解的情况：

定理1 齐次线性方程组Ax=0有非零解的充要条件为r(A)

定理2 (1)非齐次线性方程组Ax=b有解的充要条件为r(A)=r(A,b).

(2)非齐次线性方程组Ax=b有唯一解的充要条件为r(A)=r(A,b)=A的列数，即未知量的个数n.

定理3 若(Ax=b)有解，则其一般解(通解)为

x=ξ0+ξ,

ξ=k1ξ1+k2ξ2+…+kpξp

是Ax=0(称为(Ax=b)的导出组)的一般解.

注该定理给出了非齐次线性方程组解的结构.由该定理可知，要获得非齐次线性方程组的一般解，只需要求它的一个特解和它导出组的一个基础解系.

下面给出利用初等变换法求解线性方程组的具体步骤：

齐次线性方程组(Ax=0)

第一步 先用初等行变换(初等列变换)将系数矩阵A(系数矩阵的转置AT)化为行简化阶梯形矩阵U(行简化阶梯形矩阵U的转置UT)；

第二步 将U或UT改写成方程组的形式，并整理成列矩阵的形式；

第三步 写出基础解系，并写出其通解.

非齐次线性方程组((Ax=b))

第一步 先用初等行变换将增广矩阵(A,b)(增广矩阵的转置(A,b)T)化为行简化阶梯形矩阵(U,d)(行简化阶梯形矩阵(U,d)的转置(U,d)T)；

第二步 将(U,d)或(U,d)T改写成方程组的形式，并整理成列矩阵的形式；

第三步 写出(Ax=b)的一个特解及其导出组Ax=0的基础解系，根据定理3写出其通解.

例1 试用上述方法求下列齐次线性方程组的一般解:

解法一对系数矩阵A进行初等行变换化为行简化阶梯形矩阵：

x=c1ξ1+c2ξ2，其中c1,c2∈R.

解法二对系数矩阵的转置AT进行初等列变换化为UT：

后续过程同解法一.

通过上述解法可以让学生意识到解法一,也就是利用初等行变换求解线性方程组更不容易混淆.

在求解非齐次线性方程组的一般解时，我们在前面提到：需求它的一个特解和它导出组的一个基础解系.但是，在求导出组基础解系时，学生容易求成是非齐次线性方程组的线性无关的解，然后将其线性组合加上求的一个特解作为非齐次线性方程组的一般解.然而，非齐次线性方程组的解的线性组合一般不是它的解，所以这种求法是有问题的.在教学实践过程中需给学生重点强调.进一步，在雨课堂软件设置一些问答：包括对非齐次线性方程组的增广矩阵的初等变换过程、特解的选择、基础解系的选择，主要是学生易混淆的知识点等，然后在教学实践过程中让学生作答.通过学生的作答情况，对相应的知识内容进行补充强调.