火眼金睛辨真伪“独立”
——由一道试题引发的“事件独立性”的思考
金一鸣 常梨君
(江苏省常州市田家炳高级中学 213001)
概率与统计是普通高中新课程标准(2017年版)中,数学课程内容的四条主线之一,它贯穿于必修、选择性必修和选修课程.事件的独立性是概率中的一个重点和难点,它承前启后,对掌握概率求解问题有着举足轻重的地位.下面以一道有关“事件独立性”的期中试题为例,通过多角度分析,谈谈如何认清事件的独立性.
一、提出问题
例1甲乙丙三名选手参加短跑、跳远两项比赛.每项比赛以后,随机抽取一名选手进行兴奋剂检测.若每次检测每位选手被抽到的概率相同,且每位选手最多被抽检一次(第一次被抽检的选手第二次免检),则甲被抽检的概率是( ).
上题是本校高二数学期中测试中的一道选择题,考试结束后,两名学生对上题争论不休.
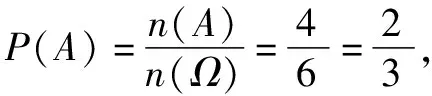

两种解法看着都对,究竟哪一种解法才是正确的呢?
二、分析研究
学生甲是利用古典概型求解.古典概型也称传统概率,是由法国数学家拉普拉斯(Laplace)提出的.在这个模型下,随机实验所有可能的结果是有限的,并且每个基本结果发生的概率是相同的.古典概型是概率论中最直观和最简单的模型,概率的许多运算规则,也首先是在这种模型下得到的.利用古典概型求解概率问题,首先要判断该试验是否满足古典概型.对照古典概型的定义,显然甲的解法是正确的.
学生乙是用事件的关系求解.高中阶段事件的关系主要有两类:互斥和独立.相应地有两个概率公式:(1)加法公式:P(A+B)=P(A)+P(B)-P(AB),特殊地,若事件A,B互斥,则P(A+B)=P(A)+P(B)(*);(2)乘法公式:P(AB)=P(A)P(B|A),特殊地,若事件A,B相互独立,则P(B|A)=P(B),即P(AB)=P(A)·P(B)(#).如果厘清事件的关系,就可以把复杂事件拆分成简单事件,从而利用概率加法和乘法公式求概率.
细看乙的解法:第一步,事件“甲被抽检”拆分成“甲第一次被抽检”和“甲第一次未被抽检且第二次被抽检”这两个事件,这两个事件是互斥的.


乙解法的错误表明,事件独立性的判定不能仅仅凭直觉,而应该用公式进行严格证明.
老苏教版选修2—3在条件概率的基础上对独立性下定义:“一般地,若事件A,B满足P(A|B)=P(A),则称事件A,B独立”,同时得到两个事件A,B独立的充要条件是P(AB)=P(A)P(B).新苏教版第二册中,独立性的定义为“一般地,如果事件A是否发生不影响事件B发生的概率,那么A,B为相互独立事件”,同时给出两个事件A,B独立的充要条件是P(AB)=P(A)P(B).
三、寻找对策
如何判断事件的独立性是教学中的一个难点,也是学生解题中的一个易错点.笔者认为教学中应从以下几个方面帮助学生提高“独立性”的判断能力.
1.利用数学情境加深独立性概念的理解
在讲解事件独立性的定义时,可以利用复杂情境,让独立性的判断不能仅仅停留在直觉判断上,必须要落到公式验证上.
例2一个家庭中有若干小孩,假定生男生女是等可能的,设A表示事件“一个家庭中既有男孩又有女孩”,B表示事件“一个家庭中最多有一个女孩”,对下列两种情形,讨论A,B的独立性:(1)家庭中有2个小孩;(2)家庭中有3个小孩.
先让学生作一下直觉的判断,然后再进行下面的计算.
解析(1)有两个小孩的家庭,样本空间Ω={(男,男),(男,女),(女,男),(女,女)},它有4个等可能基本事件,这时A={(男,女),(女,男)},B={(男,男),(男,女),(女,男)},

因为P(AB)≠P(A)·P(B),事件A,B不相互独立.

通过这个例子,使学生从中体会到对于独立性的判断不能停留在“直觉”上,有必要对随机现象作理性的研究.
2.利用“二项分布”加强独立性判断的运用

例3为了丰富学生的课余生活,促进校园文化建设,某校高二年级通过预赛选出了6个班(含甲、乙)进行经典美文诵读比赛决赛,决赛通过随机抽签的方式决定出场顺序,求决赛中甲、乙两班之间的班级数X的均值.


表1
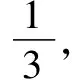
3.利用“独立性检验”升华独立性判断
在现实生活中,很多事件的概率无法准确给出,甚至会随着具体条件的不同而发生变化,比如,吸烟与患肺癌是否有关,婴儿的性别与出生时间是否有关,花的颜色与花粉形状是否有关等问题,这时需要用到独立性检验.其基本思想类似于反证法.要确认“两个分类变量X,Y有关系”这一结论成立的可信程度:其步骤如下:
(1)提出零假设H0:“两个分类变量X,Y没有关系”;
(2)在该假设下构造的统计量χ2;
(3)利用统计量χ2取值大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成立,否则认为H0成立.
判断χ2大小的标准即基于小概率值α的检验规则是:当χ2≥xα时,我们就推断H0不成立,即认为X,Y不独立,该推断犯错的概率不超过α;当χ2 第一类:两个事件独立的判定. 例4调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据表.试问能以多大把握认为婴儿的性别与出生时间有关系. 表2 分析利用表中的数据通过公式计算出χ2统计量,可以用它的取值大小来推断独立性是否成立. 解析零假设H0:婴儿的性别与出生时间无关. 故婴儿的性别与出生时间是相互独立的(也可以说没有充分证据显示婴儿的性别与出生时间有关). 第二类:两个事件不独立的判定. 例5在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.利用独立性检验方法判断秃顶与患心脏病是否有关系?你所得的结论在什么范围内有效? 分析列出2×2列联表,利用公式求出χ2与两个临界值3.841与6.635比较大小得适当范围. 解析根据题目所给数据得到表3: 表3 零假设H0:秃顶与患心脏病无关. 所以有99%的把握认为“秃顶与患心脏病有关”.因为这组数据来自住院的病人,因此所得到的结论适合住院的病人群体. 英国著名教育家贝恩布里奇说:“差错人皆有之,不利用是不能原谅的.”所以我们要充分利用好学生的“错误”资源,从课堂、作业、草稿纸等对学生“错误”资源进行深挖,把学生的错误作为其进步的起点和最近发展区,以学生的错误作为教学重难点的突破口,课堂上,让学生互动,找错误原因,作为老师适时点拨,提纲挈领,串珠成线,从而让学生“误”中有“悟”,全面提升数学核心素养.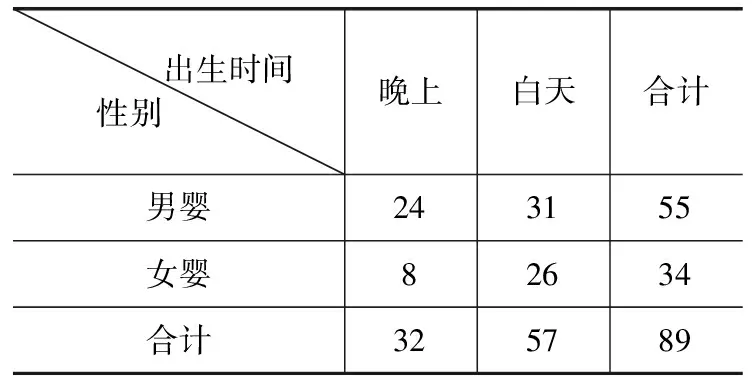



四、反思启示

