合理运用放缩法 有效破解证明不等式难题

赵 林

(山东省滕州市第二中学 277512)

证明不等式是高中数学教学难点，对学生思维的灵活性和发散性有较高要求.在证明不等式时，需要学生创新解题思路，灵活选用解题方法，才能快速、准确地解答.其中，放缩法的运用可使证明不等式问题化难为易，起到事半功倍的效果.放缩法是利用不等式的传递性，对照所证目标进行适当放缩的过程.在解题过程中，要掌握好“放”和“缩”的度，方能体现其优越性.

一、放缩法利于不等式中的求和

在证明不等式类题型中常会遇到不等式其中一边的代数式需要求和的情况，但是直接求和又比较困难，此时可通过对其进行合理的“放”“缩”转化为一个容易求和的代数式，再将其与不等式另一边相比较，从而快速得出结果.

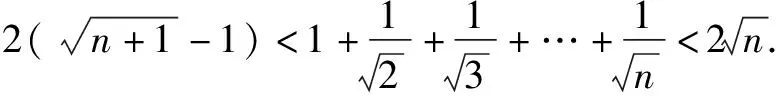
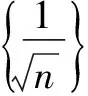
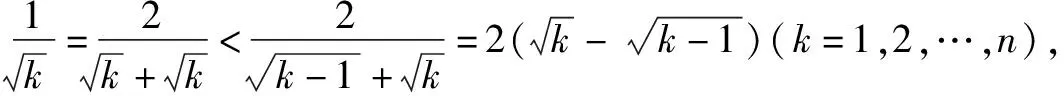
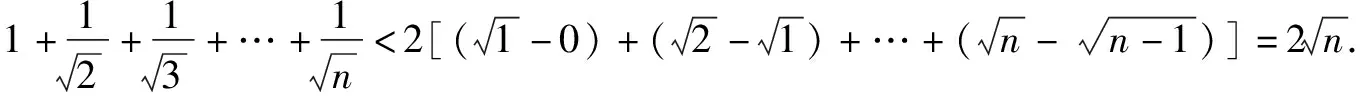
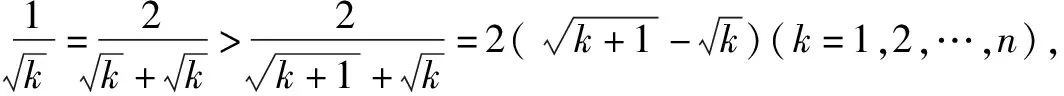
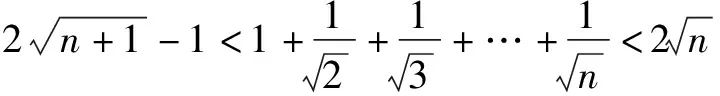
归纳本例是一道关于自然数的证明不等式问题，按常规思路通常会采用归纳法，但这将是一个纷繁冗长的过程.而用放缩法则可以化无限为有限，化难为简.本题通过将每一项适当放大，把一项折成两项之差，再求解，使解题过程更加简洁，清晰.

二、放缩法用于不等式中的求积

在上例中，难点在于证明不等式一边数列的前n项求和，同理，其求积也是解题的难点，采用放缩法同样起到事半功倍的效果.

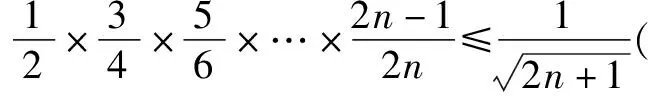
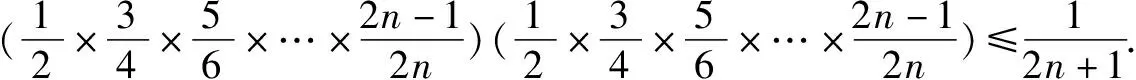
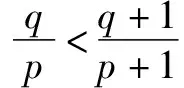
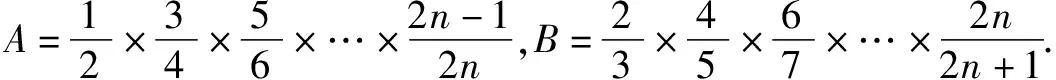
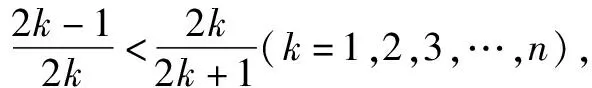
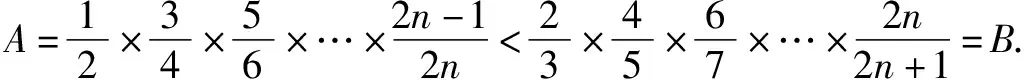
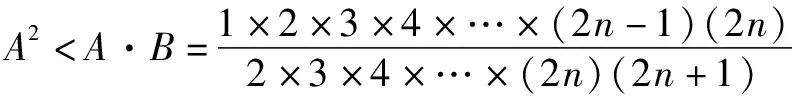
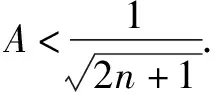
归纳在本题的证明过程中，巧妙地引用了A的对偶式B，化复杂为简单，有效简化了解题过程，突显了放缩法的魔力.当然，采用归纳法也是一种解题思路，但其繁复的过程足以使人崩溃！

三、放缩法利于减少不等式一边的变量

证明不等式题型中，如果不等式一边是常数，另一边为含多个变量的代数式，则可将此代数式看作关于这些变量的多元函数，然后对函数恰当放缩以减少函数中变量，直到求出常数.

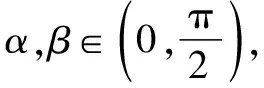
分析不等式的左边可看作关于α，β的二元函数，所以只要能求出这个函数的最小值为9即可，由于函数中包含两个变量，我们可以借助放缩法消去一个变量化简，得以求证.

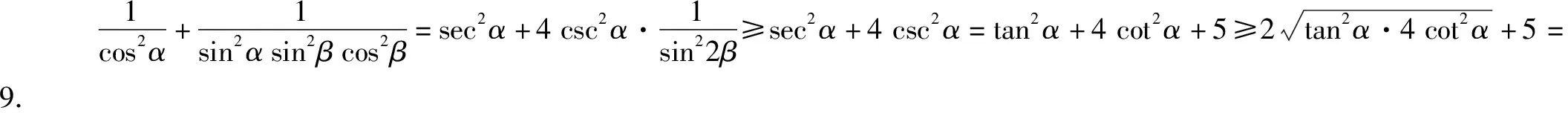
归纳在本例题中，我们可将α当作一个常数，将不等式左边看作是关于β的函数，求出函数的最小值，然后再求关于α的函数的最小值.

四、放缩法利于不等式取到等号

运用放缩法证明不等式时，最重要的是把握好放和缩的度.特别是不等式可取到等号时，每一步的放缩都不可与等号成立的条件相矛盾，否则，会适得其反.

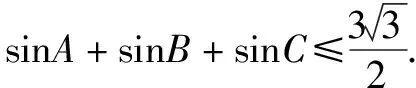
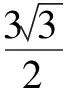
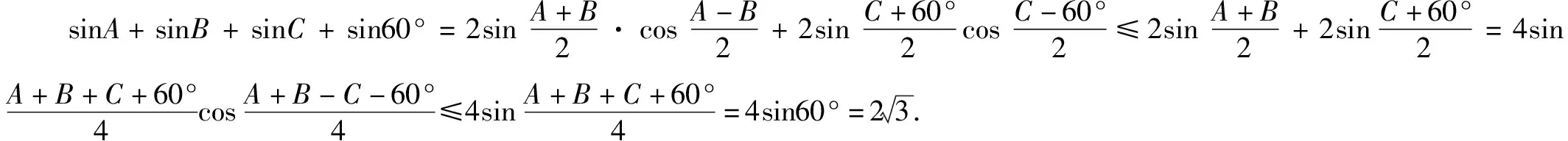
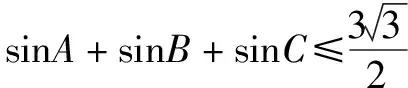
归纳在本题的证明过程中，既要注意放缩的大小要适度，以确保等号成立，又要明确放缩变形的根本目标是减少变量，以求出不等式左边的多元函数的最大值.所以，放缩法的运用要灵活适度，必须有利于简化解题过程，以便快速得出结果.

总之，高中数学中的证明不等式问题是教学难点，也是高考命题的重点.但是，我们只要坚持科学严谨的数学思想，充分利用好证明不等式的解题利器——放缩法，把握好放和缩的度，一定会让我们耳目一新，有效击破证明不等式的各种题型，提高解题效率.