西北地区铁路编组站分工优化研究

姬燕男

(1.轨道交通工程信息化国家重点实验室(中铁一院),西安 710043； 2.陕西省铁道及地下交通工程重点实验室(中铁一院),西安 710043)

1 概述

作为路网上车流到达、解体、编组、出发的技术作业站[1-3]，编组站分工直接影响货物集结发送、列车运行径路、线路通过能力、货物送达期限[4-8]等。随着 “八纵八横”高速铁路网的不断完善，西北地区铁路相关通道运输分工将发生较大变化，货运通道的升级改造，再加上资源型集运站的形成，对区域内编组站的分工将产生较大的影响。这两方面协同作用，在一定程度上可以推动西北地区的货运需求。在这种形势下，对西北地区编组站分工进行布局优化研究，将为路网规划、运输组织等提供决策支持，对保障铁路科学发展，具有现实意义。

2 西北地区编组站分工现状及存在问题

2.1 西北地区编组站现状

西北地区现状编组站和区段站主要有包括新丰镇编组站、包头西编组站、安康东编组站、宝鸡东编组站、天水编组站、银川南编组站、迎水桥编组站、兰州北编组站、武威南编组站、西宁区段站、张掖编组站、嘉峪关区段站、哈密东区段站、拉萨西区段站和乌鲁木齐西编组站。

2.2 西北地区编组站现状作业量

通过调研并收集2019年西北地区各铁路集团数据，得到西北地区现状主要编组站作业量，如表1所示。

表1 西北地区现状主要编组站现状作业量

2.3 西北地区编组站存在问题分析

目前，新丰镇编组站无调比偏低，解编作业量较大，车站解编作业能力紧张，其上行系统还承担大量的宝鸡至安康方向解编列车作业，车站作业难度大；安康东编组站上下行场到发线规模不均衡，Ⅲ场能力不足、Ⅳ场上行发车作业效率低下，影响调机运用；武威南编组站下行列车进峰前到达场与上行发车交叉干扰，且下行出发场和峰前到达场到发线能力不足；西宁编组站驼峰解体能力及调车线数量已饱和；哈密东编组站调车线能力紧张。随着研究年度货运量的增加，西北地区编组站分工也将发生变化，既有编组站布局和设施设备可能无法满足需求。

3 编组站分工优化理论基础

3.1 支点网络设计

西北地区铁路网规模庞大，在进行车流组织优化时如果完全按照路网的原始规模进行计算，将无法在可接受的时间内获得优化结果。因此需要对路网及车流的结构进行合理简化以缩减问题规模。其基本思路选取能够代表路网结构主要特征的支点网络。具体到每一个支点，主要考虑特征或者是衔接的干支线数量较多，处于路网中比较重要的位置，或者能够将他们周围的非支点站车流进行合理截流，或者是大的装卸基地，或者具有辅助截流作用[9-12]。此外，该站还要在技术设备上具有一定的规模，以适应解体、集结、编开列车的要求。结合中长期铁路网规划的全路190个支点，确定西北地区的41个支点来构成支点网络，西北地区支点网路简化示意如图1所示。

图1 西北地区支点网络简化示意

3.2 原始OD归并形成支点间车流

客流在各铁路区段上分布着大量的中间站。在实际的运输组织工作中，不同且不相邻区段上的中间站间车流往往需要通过摘挂列车或小运转列车运往技术站[13]。此过程即相当于将中间站的始发车流沿运行方向归并到了前方技术站的技术车流，而到达车流沿运行方向的反方向归并到了后方技术站的技术车流，区段内车流归并过程如图2所示。

图2 基于归并的同构变换原理示意

如图2所示，a、b、c、d分别是区段AB和区段CD上的中间站，A、B、C、D是区段端点的技术站，由a、b站发往A站及其以远的车流将被归并至A站，发往B站及其以远的车流将被归并至B站；由C站及其以远和D站及其以远到达c、d站的车流将分别被归并到C站和D站。

基于以上分析，从整股OD的视角出发，车流归并过程示意如图3所示，图3中s1，s2，…，s12是中间站，Yi，Yj，Yk是技术站。用W1，10表示从s1到s10的一小股车流。由图3可知，W1，10经过的第一个和最后一个技术站分别是Yi和Yk，那么W1，10就应该被归并到技术站Yi到技术站Yk的车流Ni.k。同样，由s1，s2始发终到s10，s11，s12的车流也应被归并入Ni.k。

图3 车流归并示意

根据以上方法，即可将中间站的小股车流归并到其附近的技术站，从而大大缩减车流OD的规模，使问题的求解成为可能。

3.3 必开直达列车去向集分析

从纯理论角度上讲，任意两个支点间均存在编开列车去向的可能性[14-15]。对于有N个点的路网来说，则可能去向数就是N(N-1)的规模。而具体到每一股OD流，改编决策变量的产生是和编组站在该方向上编组去向数相关的，或者说呈正比关系[16-23]。因此，确定满足绝对条件的必开去向，对减少决策变量规模有明显效果。指定必开去向需满足绝对条件，即

fij×min{tk}≥cimijk∈ρ(i,j)

(1)

式中，fij为i站发往j站的车流量；tk为i站至j站间第k个编组站的额外改编消耗，即有调中转相对于无调中转额外增加的时间消耗；ci为i站列车集结参数；mij为i站发至j站的列车的平均编组辆数；ρ(i,j)为i站至j站间编组站的集合。

4 编组站分工优化模型构建与求解

编组站分工合理化的主要目标是在各主要支点站之间分配合适的编解作业量，具体表现在改编负荷的分配和编开去向的多少[24]。构建编组站分工优化模型，以模拟退火算法为基础进行计算求解。

4.1 模型构建

设西北路网上41个支点站集合为V，Tij表示去向i→j产生的集结消耗，ti表示i站平均每车的无改编节省值。发站为i到站为j的固有技术车流量记为nij。定义直达直通去向优化分布决策变量如下

(2)

对于每一编组去向，定义车流吸引范围决策变量

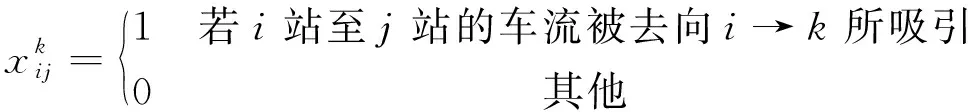
(3)

该组决策变量完全决定了车流变为列流的形式，总称为车流—列流型决策变量。这里，假设各支车流的径路是给定的。对于任意一支从i站到j站的车流，均满足以下条件

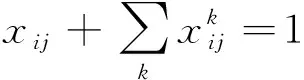
(4)

该式的含义为，当开行直达去向i→j时，从i站到j站的车流应避免在途中站改编，否则就是显然不利方案。此外，该式还限制了每支车流在具体的技术站只能并入一个去向，不能把一支车流的一部分并入甲去向，而把另外一部分并入乙去向。以fij表示由i站到j站的实际车流量(包括中转车流)。即

(5)

(6)

直达去向i→j所吸引的车流强度Dij为

(7)

显然，Dij>0时，相应地要产生一个集结消耗。路网上产生的总集结消耗为

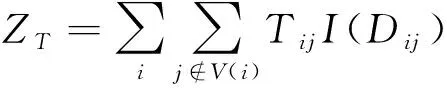
(8)

其中，阶跃函数I(x)的定义如下

(9)

而路网上所有编组站的改编消耗之和为

(10)

以编组方案的集结费用和改编费用之和最小作为优化目标；考虑到编组站的改编能力约束和调车线数量的限制，则编组站分工优化模型可表述为如下非线性0-1规划问题。

minZT+ZR

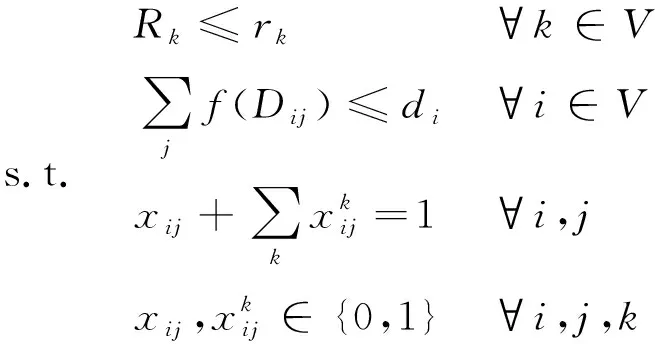
(11)

式中，rk为第k个支点站可供利用的改编能力；di为i站可利用的调车线数量；Rk为i站的改编负荷量。车流强度为Dij的编组去向i→j所应占用的股道数f(Dij)是一个受众多因素影响的复杂关系式，一般地，当Dij≤200时，该编组去向占用一个股道，当Dij增大时，酌情增加一股道。据此，一种简单的取法可以假设f(Dij)是一个连续函数，即

f(Dij)=Dij/A

(12)

这里取A=200，其中，Dij由式(7)确定。

4.2 算法求解

4.2.1 模拟退火算法概述

列车编组计划优化与编组站布局分工是一个典型的组合优化问题，是一个NP完全问题。求解这类问题的迭代过程是指数形式的。因此，诸如分枝定界法或整数规划法等严格的算法常常是不可行的。作为一种通用的随机搜索算法，模拟退火(Simulated Annealing)算法有着更好的渐近行为[25]。为了简化叙述，组合优化模型可形式化地表述为

(13)

其中Ω为问题的可行域(以下称态空间)，f:X→R+为非负目标函数。

模拟退火算法的执行策略可由如下步骤构成：从一个任意被选择的解(态)开始探测整个态空间Ω，并且通过拢动该解而产生一个新解，按照接受规则要么接受新解，要么拒绝之。模拟退火算法的一般结构可由下述伪代码描述。

给定一个初始态j0和一个初始温度T0

{

n=0;k=0;

x0=j0；

while(未达到冷凝温度){

while(未达到平衡分布){

j=generate(xk);

if(accept (j，xk，Tn))xk+1=j；

elsexk+1=xk

k++;

}

Tn+1=update(Tn);

n++;

}

}

模拟退火算法中接受概率为

(14)

温度更新函数取为几何律，即

Tn+1=αTn

(15)

式中，α∈(0，1)，取0.9。

4.2.2 车流组织优化问题的退火参数

(1)初始温度

温度初始值的选择应该保证概率密度相当于具有T=∞时的效果。即要求在初始温度值下，所有移步均以近乎于1的概率被接受，使得初始分布为常数。取

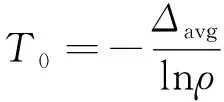
(16)

式中，分子为正能差，而ρ为给定的初始接受率。由于初始温度的高低不在于初始温度的表达式如何，而主要取决于其参数的值。ρ的取值范围在[0.85，0.98]时，计算效果已令人满意。

(2)平稳条件

若在一给定的温度值下作无限多次移步探测，则相应的马氏链可达到平稳概率分布。然而，这在实际计算中是无法实现的。现在的问题是，如何在有限量的时间内获得一个马氏链拟平稳分布。事实上，这恰恰是最少被讨论的问题。 实际计算中，可采用固定总移步数的办法。亦可采用固定马氏链长度的方法，并取每个马氏链的长度大于最大邻域的基数。

(3)算法终止准则

当模拟退火算法已产生一个很好的解，并且此时温度又足够低，这样，算法离开此解而去访问其他解的概率几乎为零。可以认为温度已降到冷凝点退火完毕。对于大规模车流组织优化问题来说，通常采用以下两个准则来终止退火过程。当连续若干次降温后，目标函数无改进，则外循环结束；当接受率小于给定的小正数ε时，则认为已达冷凝点。

在具体计算时，综合运用了以上两个准则。即当准则Ⅰ和准则Ⅱ同时被满足时，计算才终止。在准则Ⅰ中，一般需考察的温度序列为400个(即通过迭代产生400个方案选择最优解)。而在准则Ⅱ中，取ε∈[0.000 5，0.001]，从计算试验来看，这已足够。

5 计算结果分析

根据编组站分工优化模型，为了科学确定自然截流点，假设支点站截流竞争机会相等，也就是说，各个支点的改编参数和集结系数具有相同的水平。设置各支点的改编参数为3.5换算车小时，集结系数为11.5换算车小时。以2030年车流数据为基础，优化方案共计210个编组去向，其中优化去向191个，必开去向19个。部分编组去向如表2所示。

表2 西北地区编组去向

采用编组站分工优化模型和模拟退火算法，对西北地区编组站分工进行优化计算，得出新丰镇、兰州北等13个主要支点的负荷指标如表3所示。

表3 2030年西北地区重要支点负荷分布

由表3可知，2030年兰州北编组站解体编组能力仍然有富余；新丰镇能力将处于紧张状态；嘉峪关、哈密等编组站改编量在2 000车左右，存在改扩建需求；乌西的改编量达4 400车左右，也可以适当扩能。未来新兴的技术站，诸如：西宁、奎屯、库尔勒、格尔木、西宁、哈尔盖、临河等站既可作为重要支点，亦可作为大技术站加以建设。

西北地区各编组站负荷在路网上的分布如图4所示(图中灰色线条是线路，蓝色弧线是编组去向，蓝色圆饼大小表示改编量，下同)。

图4 西北区域路网相关支点改编负荷分布示意

由图4可知，兰新线西端和东端截流站分别是乌西和兰州北。若不考虑本地车流的改编量，则远程(其他支点过来在本支点改编后去往其他支点)的改编负荷如图5所示。

图5 西北区域路网相关支点远程改编负荷分布示意

由图5可知，哈密站的负荷明显高于嘉峪关站，因而其重要性也高于嘉峪关站，而格尔木站的重要性与嘉峪关站基本相同。

在编组站改编计算的基础上，对西北地区主要通道流量分布进行计算，如图6所示。

图6 西北地区主要通道流量分布示意

由图6可知，兰新铁路仍然是西北地区的货运干线，承担大部分货流出入新疆的运输任务。此外，南疆地区的部分货流也经由若羌和格尔木运往内地，格库铁路也将成为新疆货物外运的另一条重要通道。

6 结论

西北编组站分工及作业量的计算是进行铁路网、编组站规划和设计的基础。通过西北地区支点网络设计、原始OD车流归并、必开直达列车去向集等理论基础分析，以编组站集结费用和改编费用之和最小作为优化目标，同时考虑编组站的改编能力约束和调车线数量限制，构建编组站分工优化模型，采用模拟退火算法，通过标定对应模型参数来求解西北地区2030年的编组站分工及作业量。计算结果表明：在西北地区编组站的改扩建决策中，可考虑将哈密、嘉峪关、乌西、格尔木进行改扩建，新丰镇进行适当升级改造，武威南、兰州北、迎水桥等既有编组站保持当前规模，新兴技术站如西宁、哈尔盖、临河、奎屯、库尔勒等可进行适当改扩建。研究结论可为西北地区相关枢纽总图规划提供决策依据，同时为其他地区编组站分工研究提供参考。