接触式轮廓仪测量数据的建模分析与研究

朱 莉

（南通职业大学 公共教学部，江苏 南通 226007）

轮廓仪是一种两坐标测量仪器，其工作原理是：探针接触被测工件表面并匀速滑行，传感器针对被测表面的几何变化，在X（水平）和Z（竖直）方向分别采样，并转换成电信号，该电信号经放大等环节处理，转换成数字信号，以坐标的形式储存在数据文件中。在理想状况下，轮廓曲线应是光滑的，但由于接触式轮廓仪存在探针沾污或缺陷、扫描位置不准等问题，检测到的轮廓曲线出现粗糙不平的情况，这给工件形状的准确标注带来影响。

为简化问题，假设被测工件的轮廓线是由直线和圆弧构成的平面曲线。2020高教社杯全国大学生数学建模竞赛（CUMCM）D题要求，建立数学模型，针对附件1—附件4[1]所提供的轮廓仪测量数据，进行建模分析，精准计算各项参数，获取相应的轮廓图，完成文献[1]的问题1—4的研究。

1 问题1 数据定位与测量、拟合模型

问题1要求[1]：针对附件1的工件1在水平状态下的测量数据，分析其轮廓线，计算其各项参数。

1.1 用画图软件画出工件1的轮廓图

图1所示工件1的轮廓图由24段曲（直）线构成，A2~A24表示各段的分界点，A1、A25为起讫点，其中A3、A4、A7、A8、A11、A12是斜线与圆弧的切点，不太容易在图中辨识。

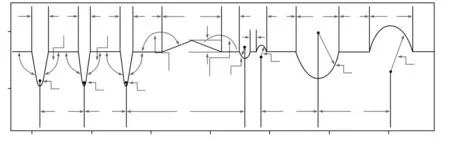
图1 工件1在水平状态下测量的轮廓线

轮廓示意图并不反映其实际尺度。将附件1表level的数据（Xj，Z）j（j是数据序号）导入画图软件（AutoCAD[2]或MATLAB），可立即生成反映实际尺度的工件1轮廓线（简称真实图）。为了求得轮廓线的各项参数值，需要确定A1~A25在表level中的数据序号。

设Ai对应的数据序号为n（ii=1~25），已知表level中的首尾序号为n1=2，n25=143 044。利用画图软件的测量功能，在真实图中测得Ai的坐标（ai，h）i（i=1~25）。由比例关系可得

1.2 用画图软件测量、计算各项参数

利用画图软件的测量功能，可直接测得真实图中的横向长度和纵向长度。因此，槽口宽度、水平线段长度x1~x13以及人字形线高度z1都可直接测得，如图1。人字形斜线长度和斜线夹角∠7、∠8可直接测量，也可按下式计算：

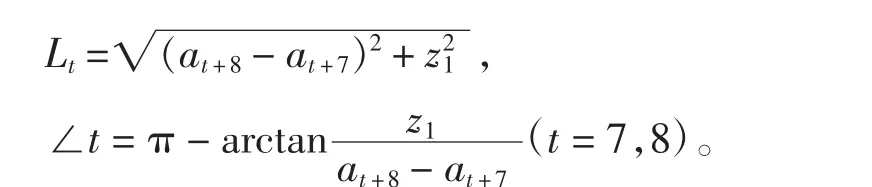
在AutoCAD中，测得的长度即实际长度；在MATLAB中，测得的长度是像素，需要按比例换算成实际长度。换算比例η（每个像素对应的实际长度）按下式计算：

其中，Xn1、Xn25为表level中的首末横坐标值，与点A1、A25相对应。

对于图1右边的4条圆弧（圆弧4—圆弧7），半径和弧长计算可参看图2。测得圆弧的横向宽度2a和纵向高度h后，由勾股定理及弧长公式，可算得半径R与弧长S：

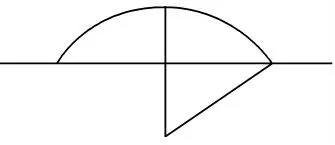
图2 待求圆弧的半径和弧长

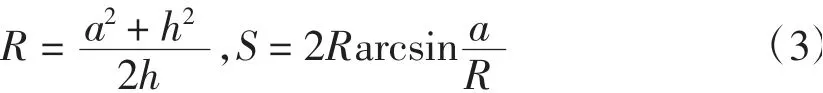
注意：由此算得的R与S，还需按式（2）换算为实际长度。同理，下文所得其他长度也要换算。

对于图1左边的3个斜槽，需计算斜线长度和夹角、底圆弧的半径和弧长等。最左边的斜槽如图3所示，O1为圆弧的圆心，F为斜线延长线的交点，其各项参数计算过程如下：

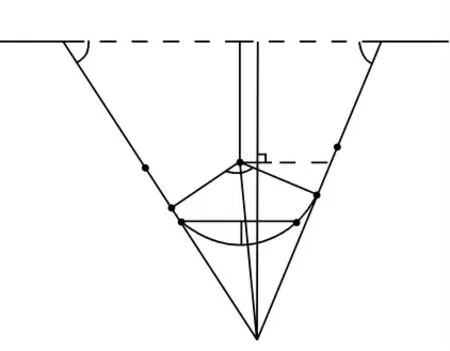
图3 求斜槽的相关参数值示意

鉴于切点A3、A4不易准确辨识，可在其上方测得点A3′、A4′的坐标（a3′，h3′）、（a4′，h4′），由此求得斜线A2A3、A4A5与水平线夹角的正切值：

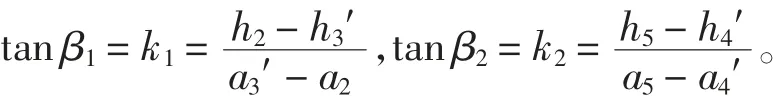
进而求得图1中的夹角：∠1=π-arctan k1，∠2=π-arctan k2。

另2个斜槽的底圆弧半径Rt、弧长St（t=2，3）、斜边夹角∠t、斜边长度L（tt=3，4，5，6）及槽口宽度的分划λt、μ（tt=2，3）都可类似求得。

图1显示，圆心距c（tt=1~6）等于相邻槽口的分划之和（右边4个圆弧的槽口分划都是槽口宽度的一半），再加上两槽口间的水平距离。具体计算式如下：

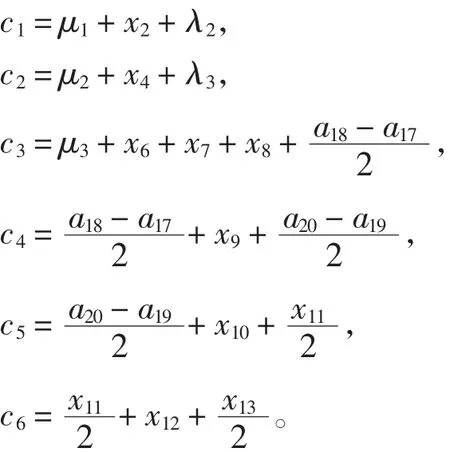
1.3 用曲线拟合法求各项参数

用画图软件测量长度和点坐标，需将光标准确放到相关点处，针对锯齿形线条手动操作，难免产生误差。

更精确的办法是直接利用表level的坐标数据（Xj，Zj）（j=n1~n25）计算各项参数。具体做法是，将表中143 043对数据分为24段，以此为样本分别拟合各段曲（直）线方程，再通过联立方程求出相关交点，进而计算所需的各项参数。

根据式（1）求得点Ai对应的数据序号n（ii=1~25），做出序号分段，第i段序号为：n

i~ni+（1i=1，2，…，24）。

这些号段的序号数目成千上万，为避免分界点归属的争议，可掐头去尾，建立序号集：

Ji=（{ni+c）i~（ni+1-d）i（}i=1，2，…，24），

选定ci，d（ii=1~24），所选数值以避开分界点为度，一般不超过200。这样掐头去尾后，样本容量仍然成千上万，不会影响曲线拟合的有效性。

在工件1的轮廓图中，有9个直线段处于同一水平线上（参看图1），可予以合并，即令

对第i=3，7，11，17，19，21，23段，以（{Xj，Z）jj∈Ji}为样本，分别拟合圆（共7个）

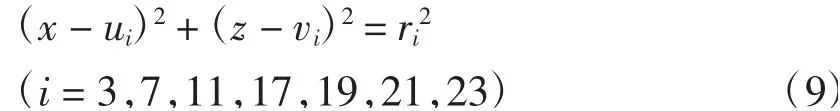
曲线拟合可用相关软件，也可在MATLAB中编程实现[3]。有了曲（直）线方程（7）、（8）、（9），就可用代数方法求出交点Ai（i=2，3，…，24）的坐标，再加上式（9）确定的7个圆的半径和圆心坐标，不需要1.2节的复杂公式，即可方便地计算各项参数。

2 问题2 水平校正的坐标变换模型

同一工件在不同次测量时，由于工件放置的角度和位置不同，轮廓线参数的计算值也会存在差异。问题2要求，针对附件1给出的工件轮廓线测量数据，计算其倾斜角度，并作水平校正后，计算其参数，比较两种测量状态下工件各项参数计算值间的差异。

2.1 倾斜轮廓图的水平校正

将附件1表down的数据导入画图软件（AutoCAD或MATLAB），可立即生成工件1的轮廓图，该轮廓图是倾斜的，需作水平校正。

运用1.1节的方法，测量分界点和端点A1~A25的坐标，按式（1）确定与表down中数据对应的序号ni，其中n1=2，n25=141 585。再按式（6）构设斜线指标集J，抽取表down中的数据（{Xj，Z）jj∈J}作为样本，拟合成直线z=kx+b。

为了厘清关系，将表down中序号为j的数据（Xj，Zj）记为点Pj（j=n1~n25），其中Pn1=A1是起始点，Pn25=A25是末位点。直线z=kx+b上与Pj横坐标相同的点记为Qj（Xj，kXj+b）。虽然Pj（j∈J）参与直线z=kx+b的拟合，但Pj（j∈J）未必恰在直线上，Qj才在直线上。

拟合所得的斜率k体现工件测量时的倾斜程度，倾斜角为β=arctan k。

水平校正采用旋转法，将直线z=kx+b旋转β角到水平位置（k>0时顺时针转β角，k<0时逆时针转β角）。旋转中心的选择非常关键，必须选取处于直线z=kx+b上的点作为旋转中心，才能将该斜线转平。因为整个图形都要旋转，所以涉及坐标变换。具体操作如图4所示，设C（x，z）为

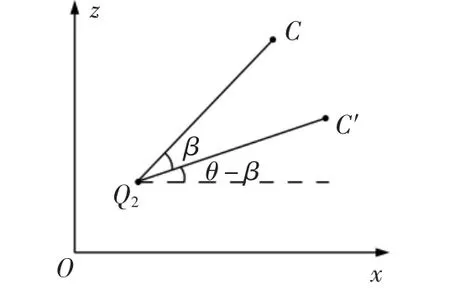
图4 旋转变换示意

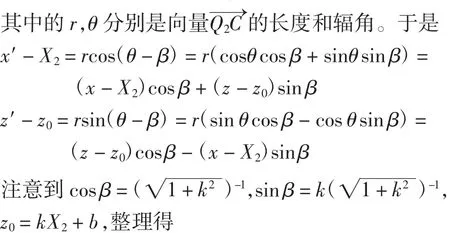
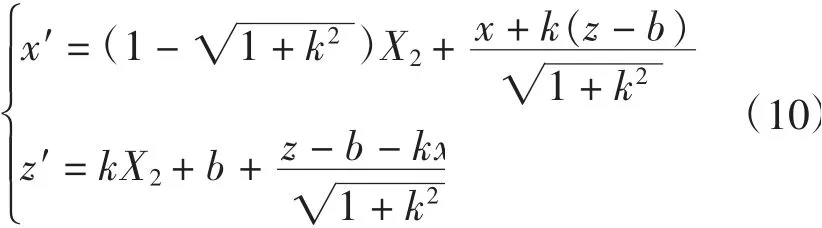
旋转中心并非一定要选起始点Q2，也可选直线z=kx+b上的其他点Q（X，kX+b）（横坐标X可任意选定）。此时只需将式（10）中X2的换成X，即可得到相应的坐标变换式。

将表down的数据（Xj，Z）j代入坐标变换式（10）的右边，得到新的坐标（Xj′，Zj′）。再将变换后的全部数据（{Xj′，Zj′）j=n1~n25}导入画图软件（AutoCAD或MATLAB），即可生成水平校正后的工件1轮廓图。

2.2 水平校正后轮廓图的各项参数

对于水平校正后的轮廓图，可运用1.2节的方法，求出槽口宽度与水平线段长度x1~x13、人字形线高度z1、圆弧半径R1~R7、圆弧长度S1~S7、斜线长度L1~L8、夹角∠1~∠8、圆心距c1~c6等各项参数。

也可运用1.3节的方法求出各项参数。因为用于水平校正的坐标变换（10）不改变数据序号，所以2.1节中获得的指标集J（ii=1~24）依然有效，且水平线z=z0已经得到，只需按式（8）、（9）拟合斜线和圆即可。

计算所得参数与问题1的结果基本相同。这是因为图形的整体旋转不会改变图形的形状和尺度，有一些小的差别是由于测量误差或计算误差所致。

3 问题3 校平比对模型

在对工件作多次检测时，每次测量实际是对整个工件中的某一部分进行局部检测。问题3要求针对文献[1]给出的工件2的10次测量数据，计算其倾斜角度和各项参数，并画出完整轮廓线。

3.1 工件2轮廓图的水平校正

附件2有10张表，分别将其数据导入画图软件后，生成10张工件2的轮廓线，这些轮廓线大同小异。相同的是左边都有两段处于同一直线上的斜线（表明测量时的倾斜度），两段斜线之间有一段圆弧，右边是折线状的角型图；不同的是轮廓线两端的缺失有多有少，可相互补充。

接下来利用拟合所得的参数k、b及自行选定的横坐标X，按式（10）实施坐标变换：

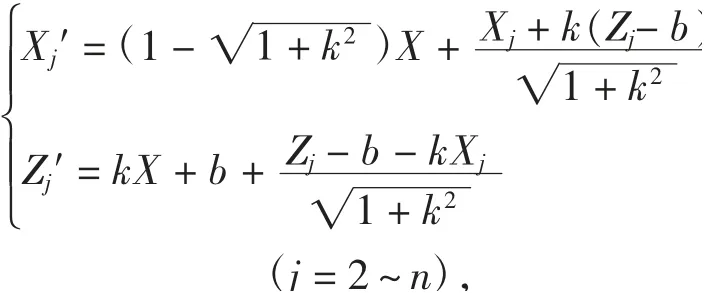
其中，每张图的坐标数据（Xj，Z）j、拟合直线参数k和b、末位数据序号n等，都各不相同。对于每张表，将变换后的全部数据（{Xj′，Zj′）j=2~n}导入画图软件，即可生成各自经水平校正的轮廓图。

3.2 画出工件2的完整轮廓线

分析上述10张经水平校正的轮廓图，比对其中2张图（如移动图形使之尽量重合），便可看出明显不合理的部分（测量误差所致）以及两端缺失情况。

在10张图中取一张作为基准（建议取左端起始部分最完整的图），依次与另9张图进行比对，逐步修正不合理的部分，添补缺失的部分。经9次修补，即可得到工件2的完整轮廓线。

然后用1.2节的测量法或1.3节的拟合法，求出轮廓线的各项参数。若用1.3节的拟合法，拟合前尚需将修补所用的数据（点）作适当平移，并调整相应的序号集。

4 问题4 局部修正的求解谋划

为了更准确地标注工件2的各项参数，问题4要求利用附件3、4提供的工件2关于圆和角的9次局部测量数据，修正问题3的结论，并进一步修正工件2的完整轮廓线。

4.1 圆弧局部的进一步修正

附件3有9张表，均为工件2轮廓线中左部两段直线夹圆弧的局部测量数据。对于每张表，分别采用3.1节的方法，拟合直线z=kx+b，利用获得的参数值k和b，实施坐标变换，将变换所得数据导入画图软件，可生成9张经水平校正的两线夹圆弧局部轮廓图。

用3.2节的方法比对上述9张图，修正明显不合理的部分，得到最准确的局部轮廓图，再用其替换3.2节所得完整轮廓线中两线夹圆弧的局部，实现对圆弧局部的进一步修正。

4.2 角型局部的进一步修正

附件4也有9张表，均为工件2轮廓线中右部折线状角型局部的测量数据。将9张表的数据分别导入画图软件，生成9张工件2的角型局部轮廓线。结果表明，9张图形状类似，左部都有一直线段。

和4.1节一样，经直线拟合、坐标变换，生成9张经水平校正的角型局部轮廓图。然后比对这9张图，修正明显不合理的部分，得到最准确的角型局部轮廓图。再用其替换4.1节得到的经圆弧修正后的完整轮廓线中折线状的局部，便实现了对角型局部的进一步修正。