直升机定位悬停控制律的设计及仿真
刘彦涛 李 雨
(陕西东方航空仪表有限责任公司,陕西 西安 710100)
0 引言
由于直升机具有使用灵活、机动性强的特点,因此它被广泛运用于民用和军事领域。在直升机的控制系统中,低空悬停控制系统是其不可或缺的一部分,它能使直升机保持在一定高度、航向和水平位置的飞行状态,这种飞行特性是直升机特有的。在悬停过程中,极易受外界环境的干扰,环境风对直升机的影响很大,位置很容易受风扰动出现较大的偏差,尤其是在复杂风场下,风场动态变化,直升机保持位置的难度更大[1]。
因此,为了提高直升机定位悬停的稳定性和精度,非常有必要为直升机设计专门的定位悬停控制律,消除因外界扰动而出现的速度静差,并抑制风干扰造成的位置漂移。
1 直升机模型
1.1 建模概述
直升机数学模型是设计定位悬停控制律的基础,它是由计算风洞数据而得出的直升机小扰动模型,该模型描述了直升机的输入、输出特性,此外,执行机构也是直升机控制回路中必不可少的一部分,该机构可以为直升机提供必要的机械传动。该小节简要地对直升机的状态模型和执行机构模型进行描述。
由于直升机的运动机理极其复杂,因此为了便于分析,在建模时应充分考虑主要因素并忽略次要因素,从而达到简化模型的效果。在直升机的建模过程中主要考虑了以下3个因素[2]:1)将直升机视为刚体,忽略直升机弹性形变和旋翼姿态变化的影响。2)忽略地球的自转与公转,将地面坐标系视为惯性坐标系。3)假定直升机机体坐标系的XOZ平面是机身的对称面。
1.2 直升机状态方程
利用直升机的小扰动假设,以给定高度为H0、速度为V0下飞机的水平直线飞行为基准状态,在基准状态下,俯仰角速率的初始值()、倾斜角速率的初始值()、航向角速率的初始值()、俯仰角的初始值(θ0)、倾斜角的初始值(φ0)、航向角的初始值(ψ0)、侧向速度的初始值(v0)以及法向速度初始值(w0)都为0。根据直升机的动力学方程推导出飞机的状态方程如公式(1)所示。

式中:X为状态向量;A为状态矩阵;B为输入矩阵;U为输入向量。
1.3 直升机状态方程
舵回路是飞行控制系统的重要组成部分,它是飞行控制系统中的重要驱动环节。舵回路是非线性控制回路,传动是舵回路的重要组成部分[3]。为了便于制定控制法,必须在某些条件下简化该法。
直升机的执行机构主要包括舵机和助力器等,它们负责将控制信号转换为相应的机械位移或力。该环节通常具有一定的非线性,在设计过程中对其进行了简化处理。由于各通道执行机构的建模方法和思路相似,因此下面仅以俯仰通道执行机构为例予以说明。俯仰通道的执行机构如图1所示。
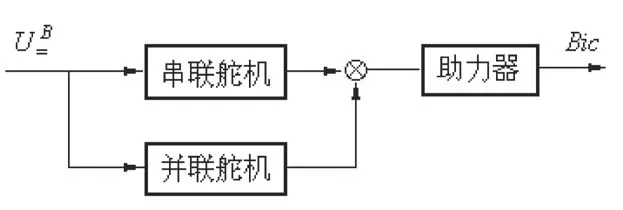
图1 俯仰通道执行机构图
在图1中,舵机由串联舵机和并联舵机组成,串联舵机存在毫秒量级的延迟,为了便于分析,忽略延迟造成的影响,视串联舵机为比例环节。并联舵机是由带死区的饱和环节和积分环节串联而成的,当出现小扰动时,可以不考虑并联舵机的影响;当出现大扰动时,则可以将其视为积分环节。其中,助力器为一阶惯性环节。
2 定位悬停控制律设计
2.1 系统整体设计
直升机定位悬停控制是一种精准位置控制,其控制算法是基于直升机悬停状态而设计的,包括对纵横向位置、纵横向速度及内回路姿态的综合控制。
为了解决影响直升机定位悬停的因素,应对系统进行整体设计,控制律框图如图2所示,图中虚线框部分为基于速度的位置定位悬停控制结构。
在图2中,直升机定位悬停控制中的位置控制算法是1个PI控制器,通过飞行控制计算机接收给定的直升机地面位置坐标,与INS/GPS组合导航系统提供的当前的地面位置坐标构成PI反馈控制,计算出达到指定位悬停所需要的速度,并将其输入速度控制回路中,速度控制回路计算出直升机达到指定飞行速度的下一步飞行姿态,将其输入姿态控制回路中,通过姿态控制回路的调整,改变直升机的飞行姿态,从而使直升机向期望的地面控制位置进行飞行调整[4]。
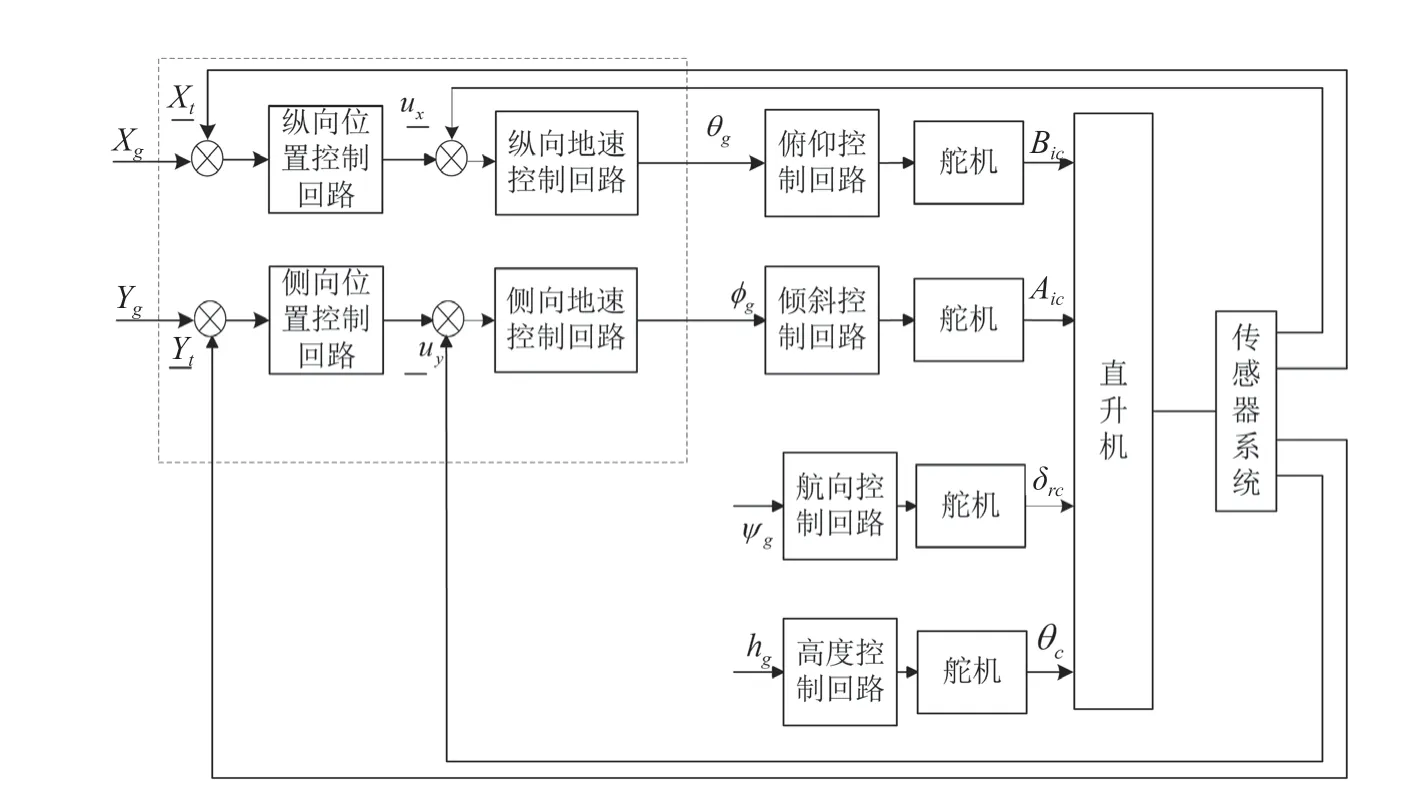
图2 直升机定位悬停系统控制框图
当直升机达到给定的地面位置坐标后,位置控制回路的输出为0,直升机保持地面位置、航向及高度的稳定,再进入精准的定位悬停状态。
以纵向通道控制为例,其具体控制原理如下:将给定纵向位置的地面坐标与实际地面位置坐标进行比较,得出偏差值,通过纵向位置控制器计算纵向速度控制量,将产生的控制量与纵向速度的反馈量进行综合,其输出结果作为俯仰角的给定指令,进而控制纵向周期变距的改变,使直升机的纵向位移偏差为0,稳定在指定的位置上。
高度通道和航向通道采用前飞模态中的控制方式,按照指定指令保持航向和高度不变。以下重点介绍直升机定位悬停模态中纵向通道和横向通道的控制律设计,包括俯仰、倾斜通道的姿态控制、地速控制和位置控制。
2.2 姿态控制回路
姿态控制回路是直升机飞行控制中最为重要的一个部分,其直接影响直升机飞行的稳定性和姿态的可控性,是实现位置控制的基础,其性能直接决定了直升机的飞行性能。纵向通道俯仰角控制回路和侧向通道倾斜角控制回路的控制框图如图3所示。
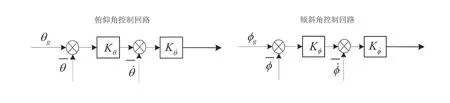
图3 姿态角控制框图
姿态角控制回路主要是通过反馈姿态角位置来实现姿态增稳;设计姿态角的控制回路时,使用角位置和角速率双闭环控制,可以有效地提高系统的动态响应,改善系统的阻尼特性,从而改善系统的动态稳定性。
2.3 地速控制回路
设计地速控制回路是为了消除直升机在悬停时受到阵风或者常值风扰动后出现的速度静差。纵向地速和侧向地速的控制框图如图4所示。
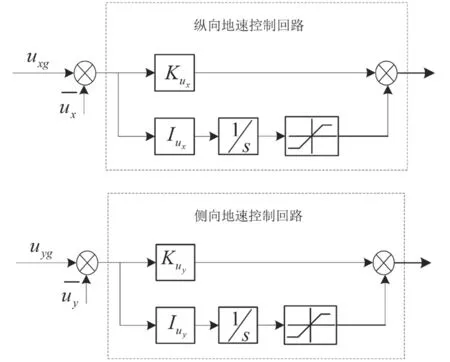
图4 地速控制框图
地速控制回路由比例和积分构成,该控制回路计算出直升机达到指定飞行速度的下一步飞行姿态,并将结果输入姿态控制回路中。需要在地速控制回路的积分环节中施加限幅环节,从而避免因积分过大而导致舵面饱和。
一般在速度控制回路中引入速度的微分可以改善速度动态响应的平稳性,但是在该设计中,省略加速度项的主要原因如下[5-6]:1)信号质量问题。由于直升机的升力是由旋翼机构产生的,且旋翼是一个灵活的部件,因此作用在旋翼上的可变载荷容易引起高频振动,机身在悬停状态下不稳定,这容易传递到机身,导致机身产生振动噪声、信号特征相似性的问题。2)信号特征相似性问题。在飞行阶段,直升机机身姿态与加速度之间存在相关性,内部环路倾斜角的信号反馈能够使反馈加速度效应更加接近。与姿态角信号相比,加速度信号相对较小,因此可以省略加速度反馈。3)简化配置。降低成本。
2.4 位置控制回路
地面速度检测环路只解决了地面速度跟踪的问题,绝对位置跟踪需要位置周期的干预。地面速度受到干扰后,可能会恢复到原来的状态,因此有必要设计一个基于速度检测环路的位置控制系统[5]。
位置控制周期对应地面速度控制环路的外部环路,其主要功能是通过直升机的实际位置和反馈位置指令之间的偏差产生期望的地面速度指令,并将其发送到地面速度控制环路,实现对位置的跟踪和控制。纵向位置和页面位置控制图如图5所示。
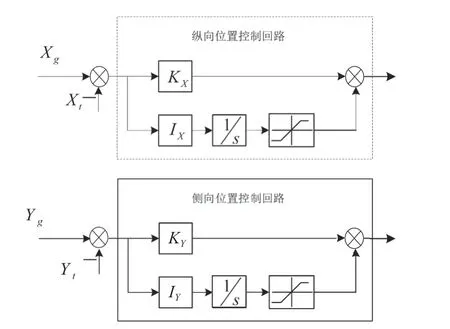
图5 位置控制回路
采用比例综合控制结构,位置积分信号通过边界线,防止出现地面速度指挥过快的情况。在位置控制回路中添加积分术语的目的是提高悬停位置的控制精度。当存在外部干扰时,静态位置错误必须通过集成来消除,但位置集成容易引起振荡,因此位置集成只能是弱集成。在干扰的早期阶段,直升机的整体几乎无法工作,整体概念只能在随着时间的推移积累到一定大小后才能消除稳定状态错误。但是,地面位置可以在干扰的早期阶段从位置误差生成反向地面速度命令,位置误差越大,反向地面速度命令就越大。在地面速度控制环路的作用下,位置误差可以快速地被消除。该机制可以抑制初始扰动阶段的位置误差,提升直升机定位悬停的效率。
3 仿真验证
3.1 速度控制设计仿真
速度控制环节设计为比例加积分PI控制结构,输出为内环姿态控制的输入,设定好控制参数,分别给定纵向速度和侧向速度1 m/s的阶跃指令[7],纵向速度Δu和侧向速度Δv的响应曲线如图6所示。
由图6可知,纵向速度超调量为7%,调节时间为24 s,无稳态静差;侧向速度无超调,调节时间为14 s,无稳态静差。纵向速度和侧向速度均满足设计要求。

图6 速度响应曲线
3.2 位置控制设计仿真
在速度控制回路的基础上,设计外环位置控制,采用比例加积分PI控制结构,反馈采用速度输出的积分,输出为内环速度控制的输入。设定好控制参数后,给定纵向和侧向位置1 m的阶跃指令[7],纵向位置ΔX和侧向位置ΔY的响应曲线如图7所示。
由图7可知,纵向位置和侧向位置最终均能很好地跟踪给定的位置指令,且无稳态静差,满足设计精确定位的要求。
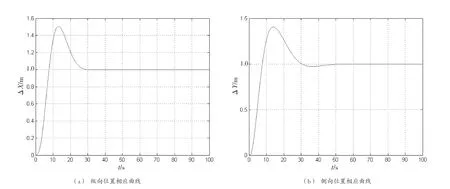
图7 位置响应曲线
4 结论
无人直升机因其具有机动灵活、定点悬停等独特的飞行性能而日益成为国内外无人机研究的热点之一。从飞行和气动特性上划分,直升机可以分为起降、悬停/小速度以及前飞等3个阶段,各个阶段也表现出不同的物理特性,其中悬停/小速度段是直升机所特有的飞行阶段,飞行时存在稳定性差、纵横向耦合严重、旋翼操纵功效低、姿态抖动严重以及速度测不准等一系列问题;同时,悬停/小速度飞行还是无人直升机执行任务最常用的飞行阶段。
该文设计的直升机定位悬停控制律,包括直升机内环姿态控制、中间速度控制和外环位置控制,设计架构合理可行。经仿真验证,直升机的位置可以无误差地稳定在设定的指令位置,设计的定位悬停控制律及参数正确合理,满足工程实际应用的需求。
后期,在该设计的基础上,可以针对直升机在不同高度、速度状态下,对控制参数进行优化,满足全包线的设计需求。

