弱电网下提高VSG稳定性的虚拟阻抗方法

施 凯，陈 磊

（江苏大学 电气信息工程学院，江苏 镇江 201013）

0 引言

由于传统能源的日益减少，清洁环保的可再生能源成为很好的替代品，分布式电源作为新能源的主要部分，装机量在电网总发电容量中占比越来越大[1]。然而新能源大多地处偏远，导致分布式电源从长距离的不同地点并入电网，电网等效阻抗增大，逐渐表现出弱电网特性，并网逆变器出现谐波等影响运行和稳定性问题[2]。VSG在电网系统中加入了惯性和阻尼，成为当前并网发电技术的研究热点[3]。

在弱电网情况下，电网阻抗对VSG的并网运行产生影响[4,5]。文献[6]与文献[7]对VSG的功率环进行小信号建模，并同时考虑稳定性的影响，对控制环节的参数进行了整定，但未研究VSG在弱电网下出现的问题。文献[8]推导了 VSG的小信号模型，揭示了功率响应与电网电压扰动的关系，但是无法反映电网强度对系统的影响程度。文献[9]通过谐波线性化的方法对VSG进行序阻抗建模，分析了电网强弱以及不同数量 VSG并网时对系统的影响，但未提出弱电网对 VSG造成影响的解决方法。文献[10]通过改变有功环的参数提高 VSG在弱电网下的稳定性，但有功环参数的调节对 VSG本身的稳态和动态性能产生影响。

本文针对弱电网条件下，VSG并网运行的稳定性问题，首先，在dq坐标系下对VSG建立了阻抗模型，并对其频率特性进行分析研究；然后，根据广义奈奎斯特判据，讨论了电网强弱与VSG稳定性之间的关系，揭示了 VSG系统在弱电网情况下运行失稳的机理；提出了通过虚拟阻抗的方法提高VSG稳定性的方法；最后，在MATLAB中进行仿真，证明了理论分析的正确性。

1 VSG控制原理

图1为VSG拓扑图，图中Udc是直流侧电压，Qi为IGBT器件（i=1～6）；ea、eb和ec为VSG的内电势；L1和L2为滤波器电感；C1为滤波器电容；uk和ik分别为VSG输出电压和输出电流（k=a、b、c）；Lg为电网电感；ugk为电网电压。

图1 VSG拓扑结构Fig. 1 Topology of VSG

VSG参考了同步发电机的控制方法，图2给出了VSG的详细控制框图。图中Pset、Qset为控制环节中给定的参数值；P、Q为VSG实际输出的功率值；J和DP为引入的虚拟惯量和阻尼系数；DQ为无功调节系数；ω0和ω分别为电网角速度和VSG角速度；Ug为电网额定电压幅值；Em和θ分别为VSG输出电压幅值和相位。

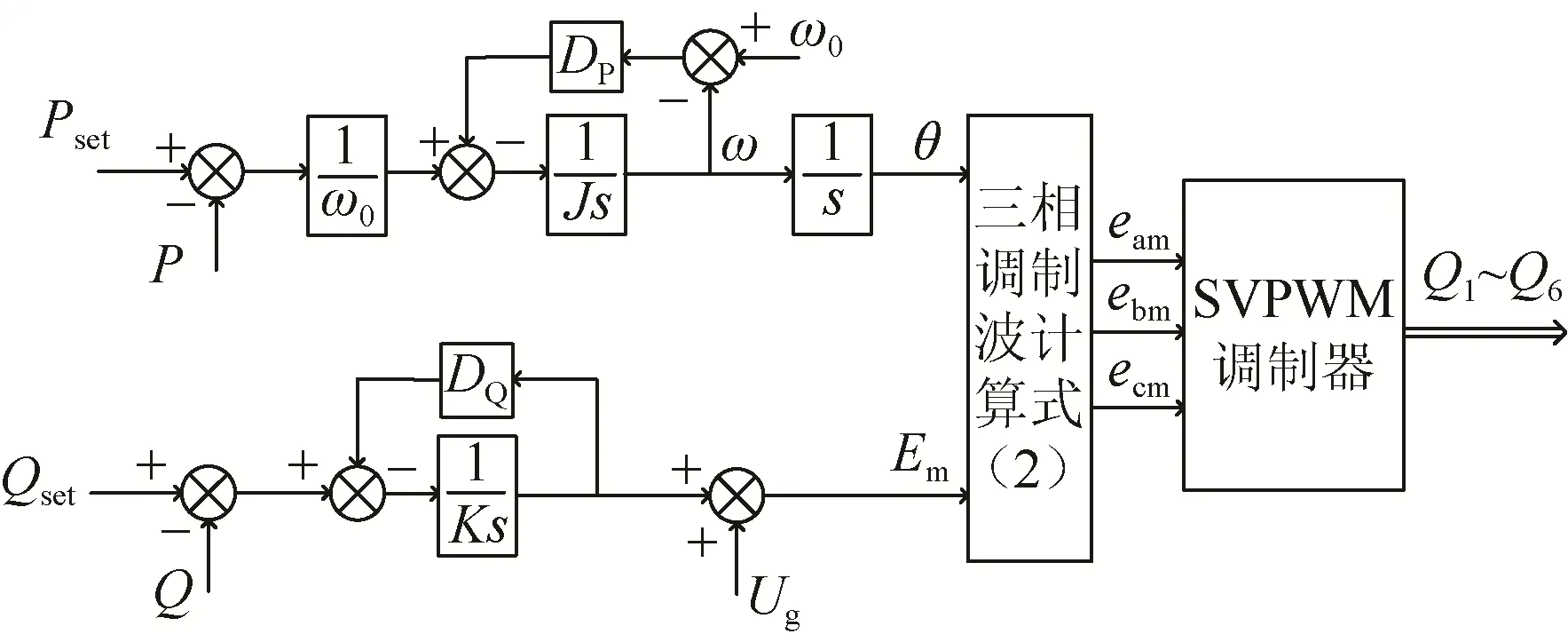
图2 VSG控制结构Fig. 2 Control structure of VSG

图2中P、Q由uk和ik计算得出：

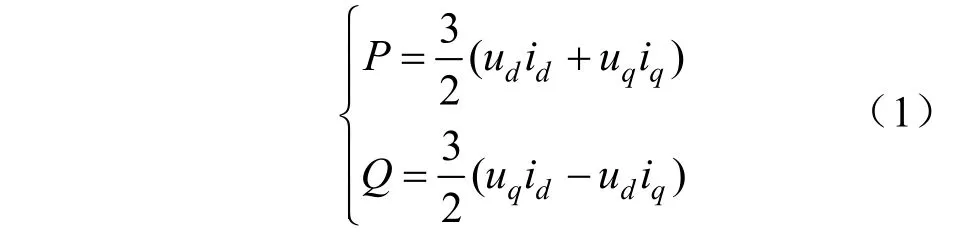
VSG的调制波由功率环的输出Em和θ计算得到：

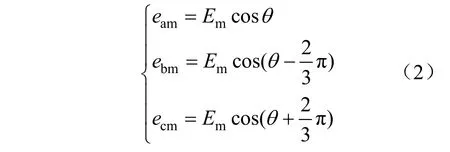
2 VSG系统阻抗建模

由于 VSG具有周期性非线性时变的工作特性，传统小信号分析的方法不适用。本文采用dq轴线性化的方法对VSG输出阻抗建模，对小信号扰动产生的响应进行分析，即可获得VSG输出阻抗模型。图3为VSG小信号模型。由于只研究VSG的交流侧，将直流扰动量赋值为0。

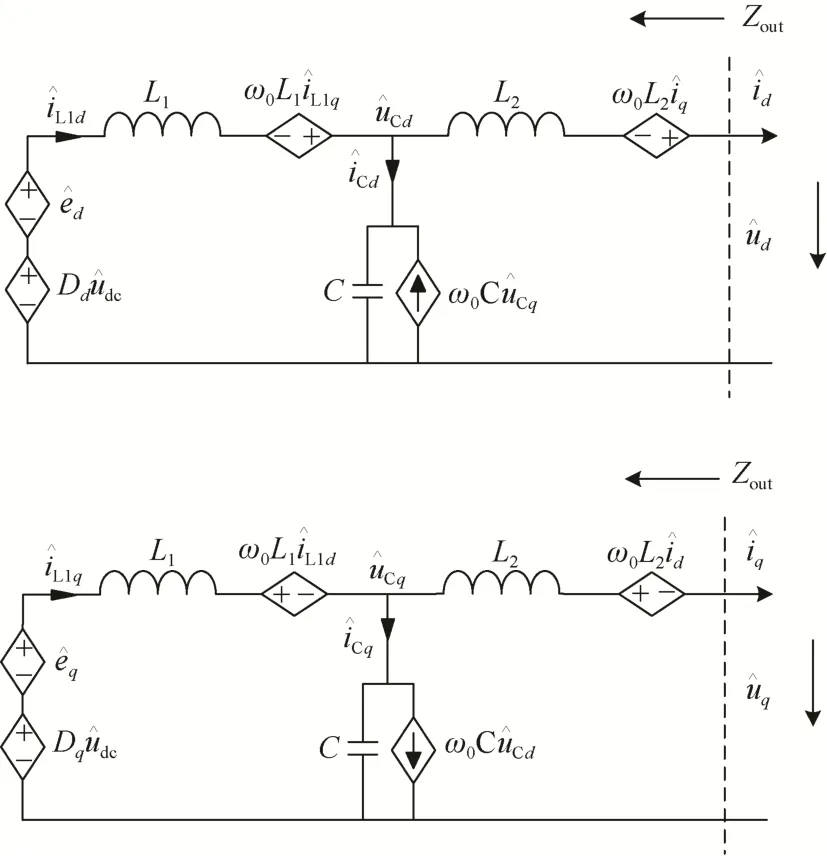
图3 VSG在dq坐标系下的小信号电路模型Fig. 3 The small signal circuit model of VSG in dq coordinate system

由图3可得，系统在dq坐标系下的表达式为：

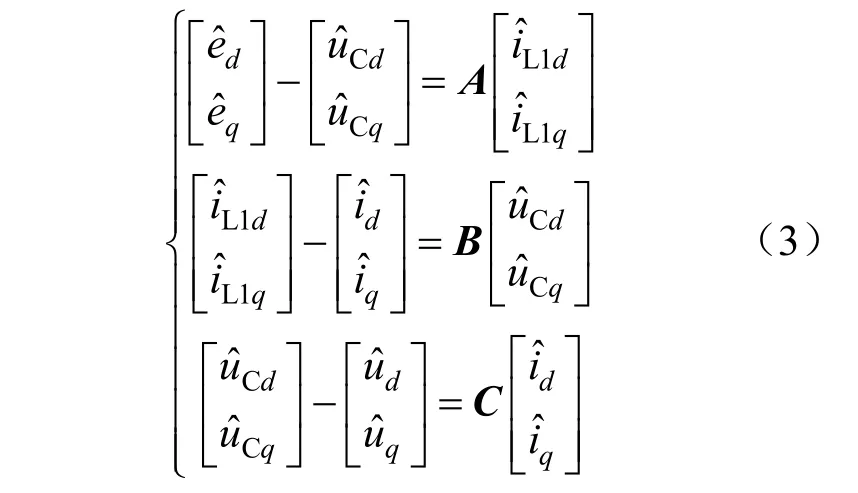
其中：

图4为VSG的小信号模型，小信号扰动项包括d轴分量和q轴分量，在VSG控制策略中，有功功率P，无功功率Q为给定信号量，在控制过程中数值保持不变，可认为给定功率的扰动为0。

图4 VSG小信号模型Fig. 4 Small signal model of VSG

由VSG输出阻抗的定义可得Zout表达式为：

根据图3中VSG主电路模型中的电压、电流关系，可以得到F1、F2的表达式：

式中：I二阶为单位矩阵。

P0和Q0是VSG正常稳定工作时的功率值，加入扰动后可得：

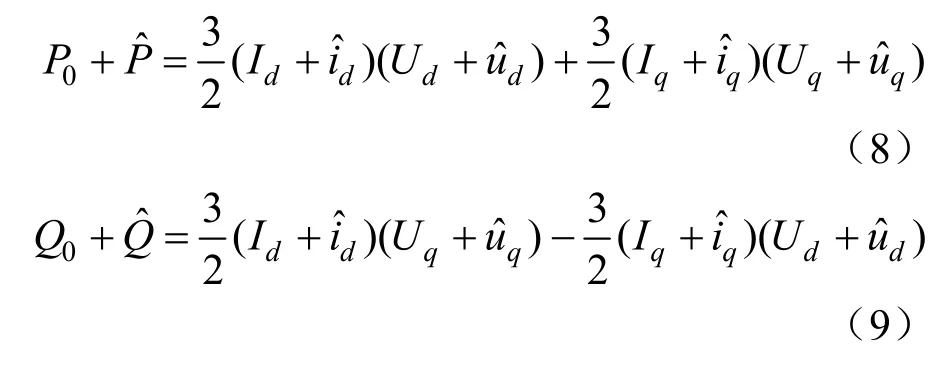
将式（8）（9）展开并消除稳态值可得：

根据图 4所示的小信号模型以及式（10）可得F3和F4的表达式：

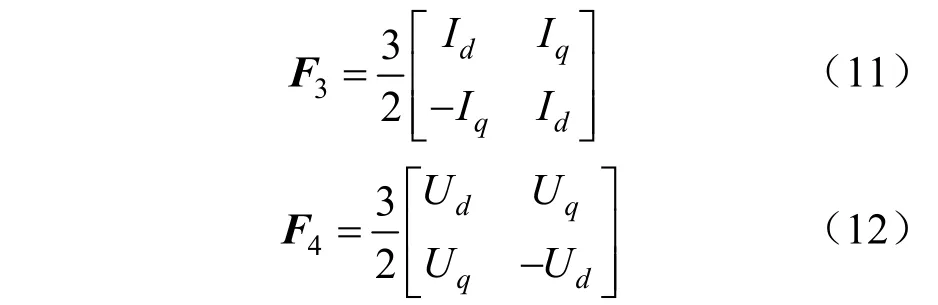
图4中F5为VSG功率环的传递函数矩阵，对图2进行分析，由于ω0和Ug都为额定值，并且其大小不受扰动的影响，可得F5表达式：

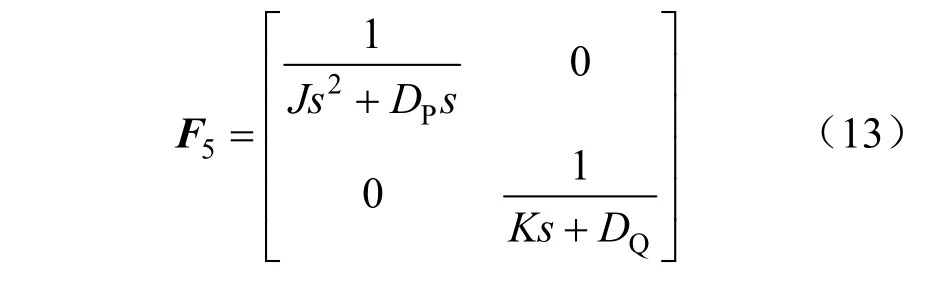
为VSG输出电压幅值扰动；ˆ为相位扰动；和分别为dq坐标系下的扰动表现形式。

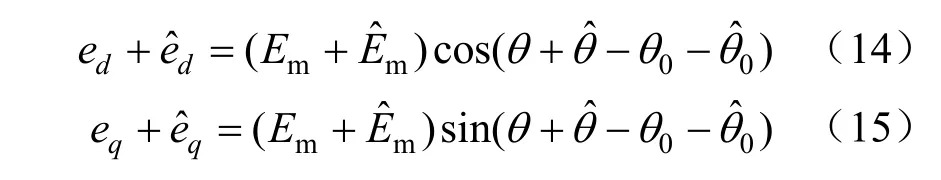
式中：θ0为电网电压相位。

将式（14）展开并消去二阶扰动项和稳态值可得：

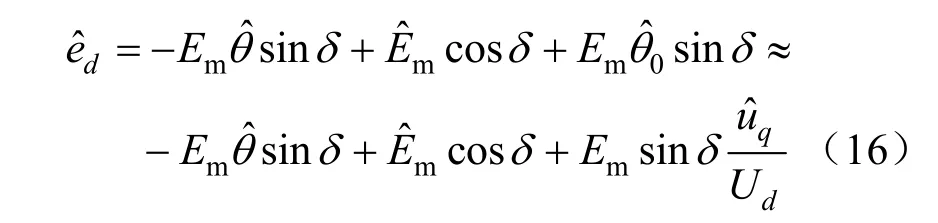
式中：δ为VSG输出内电势与电网电压的相位差角。

同理对式（15）进行相同处理可得：

将式（16）（17）写成矩阵形式：

根据图 4所示的小信号模型和式（18）可得传递函数矩阵F6和F7的表达式：

根据上述分析可得输出阻抗Zout的表达式：

3 VSG接入弱电网的稳定性分析

对Zout表达式进行分析，可以得到Zout的频率特性，对其分析可得VSG在弱电网下的运行稳定性。

在弱电网中，电网阻抗不可忽略。因此，Zg的表达式为：

电网强弱按照短路比SCR进行区分，SCR定义为：

式中：SCR为PCC点的短路容量；SN为VSG额定容量，本文所取的VSG额定容量为7 kW。

通常情况下认为SCR大于20的电网为强电网，SCR小于10的电网为弱电网[11]。取电网电感Lg=3 mH（SCR=22）模拟强电网，电网电感Lg=15 mH（SCR=4.4）模拟弱电网。

图5为Zout和Zg的伯德图。由图中曲线可知，在低频范围内VSG输出阻抗伯德图的dd分量具有正电阻特性，qq分量具有负电阻特性。在高频范围内Zout的dd分量和qq分量均呈现电感特性。其中，由于qq分量中出现负电阻特性，导致VSG的运行稳定性出现问题。

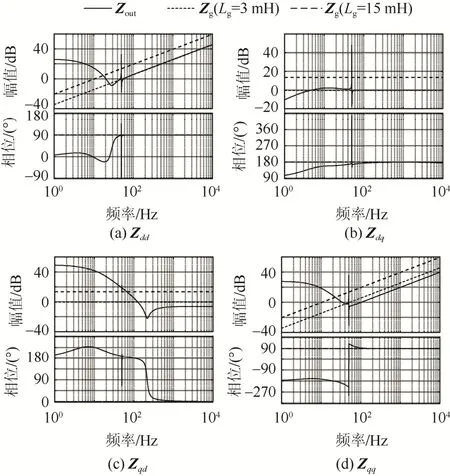
图5 输出阻抗与电网阻抗伯德图Fig. 5 Bode diagram of output impedance and grid impedance

VSG并网运行的稳定性可以通过回率矩阵L是否满足广义奈奎斯特判据来判断[12]。L的表达式为：

当L的每个特征函数曲线都不包围（–1，j0）点，则判定系统是稳定的。

图6为不同电网阻抗取值时L的特征根轨迹。当Lg=3 mH时，λdd和λqq曲线都没有包围（–1，j0）点，系统能够稳定运行；当Lg=15 mH时，λdd曲线没有包围（–1，j0）点，而λqq曲线包围（–1，j0）点2次，系统运行不稳定。

图6 不同电网阻抗下L的特征轨迹Fig. 6 Characteristic trajectories of L under different grid impedances

4 VSG输出阻抗校正

由图3所示的VSG与电网的等效电路，可以推导出：

由式（25）可知，提高VSG输出阻抗Zout的模值，可以减少电网阻抗Zg对并网电流以及VSG运行稳定性的影响。

由式（21）可知，改变有功环和无功环中的参数可以提高VSG输出阻抗，但改变功率环的参数会对VSG的动态稳定性能产生影响。所以，本文提出使用虚拟阻抗的方法，不影响VSG本身的动态性能。

4.1 串联虚拟阻抗

针对VSG输出阻抗的改造，可以通过串联虚拟阻抗Zv来实现。如图7所示，此时VSG等效输出阻抗为：

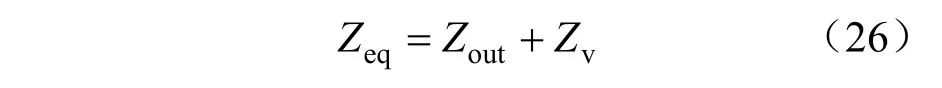
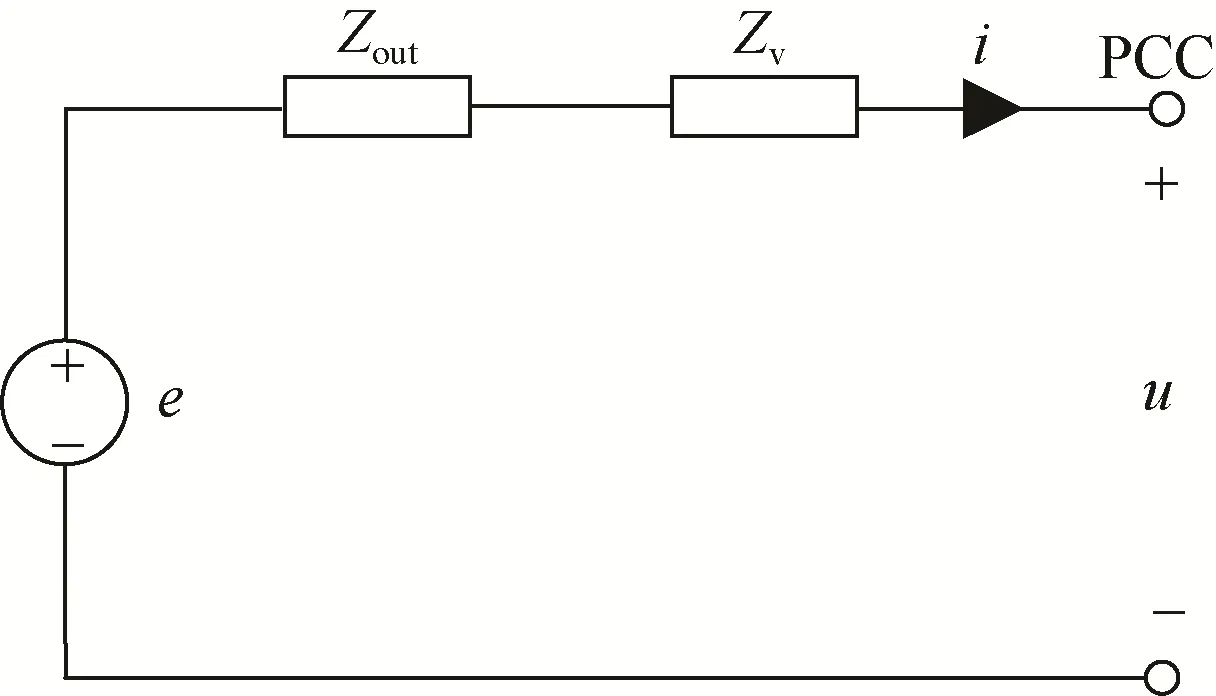
图7 串联虚拟阻抗校正方法Fig. 7 Correction method of series connection virtual impedance

当虚拟阻抗Zv取值为正时，输出阻抗Zeq具有抬升效果，下面具体分析Zv的取值范围。

由于串联虚拟阻抗后，VSG的输出电流会出现一定的偏差，而VSG给定输入为功率，进而对输出电压产生误差，因此需限制Zv的大小。

假设Zv引入的电流误差为EA，则EA的表达式为：

式中：ω0为基波角频率。由于在频率ω0处串联的虚拟阻抗值为正常数且远小于输出阻抗，因此：

当电流误差取到最大时，虚拟阻抗的最大值为：

图8给出了串联虚拟阻抗的实现方法：将并网电流i乘以Zv获得串联阻抗的电压uzv，并从等效电压源e中减去该电压。

图8 串联虚拟阻抗的实现Fig. 8 Realization of series connection virtual impedance

4.2 并联虚拟阻抗

采用并联虚拟阻Zv进行校正时，如图9所示，VSG等效输出阻抗和等效电压源为：

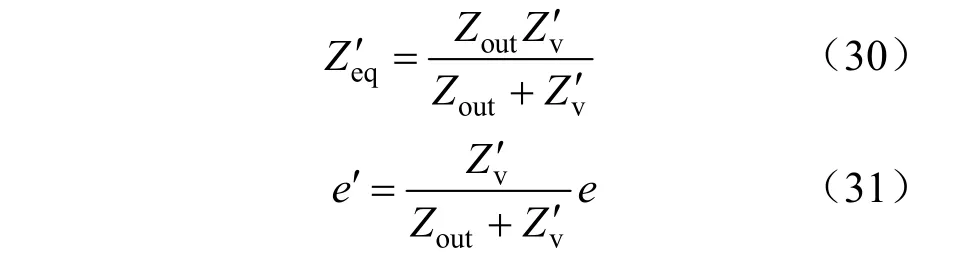
图9 并联虚拟阻抗校正方法Fig. 9 Correction method of parallel connection virtual impedance

由式（30）可知，虚拟阻抗′取负值时，等效输出阻抗的模值可以得到提高。由式（31）可知，并联虚拟阻抗会影响等效电压源的误差，以下分析的取值范围。

假设′引入的电压源误差为EV，则：

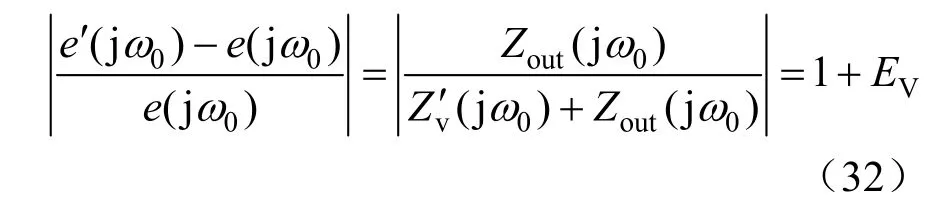
由于并联的虚拟阻抗值为负值，在给定允许最大误差EV_max时，′最小值为：

图10为并联虚拟阻抗的实现方法，其中，将并网电压u乘以虚拟阻抗′获得电压分量，并将该电压分量加到等效电压源e中。

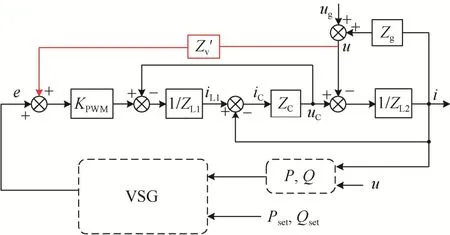
图10 并联虚拟阻抗的实现Fig. 10 Realization of parallel connection virtual impedance

5 仿真验证

为了验证本文所提的方法，在MATLAB中搭建了VSG并网的仿真模型，参数如表1所示。

表1 仿真主要参数Tab. 1 Main parameters of simulation

根据本文的研究分析，为了提高VSG对弱电网的适应性，需要在控制结构中加入串、并联虚拟阻抗来改变等效输出阻抗。使用串联虚拟阻抗的方法时，对VSG的输出电流产生影响，需要对Zv的取值进行约束，要求产生的输出电流误差最大为EA_max=2%，根据式（29）可求得Zv_max=0.06。当并联虚拟阻抗时，为了降低对等效电压源产生的误差，要求最大误差EV_max=1%，根据式（33）可求得Zv_min=−0.029。

图11为加入虚拟阻抗环节后，弱电网下回率矩阵L特征函数λqq的轨迹与传统VSG控制下的对比。从图中可以看出，由于串、并联虚拟阻抗的作用，特征值λqq的曲线由包围点（–1，j0）两次变成不再包围，VSG的运行状态趋于稳定。

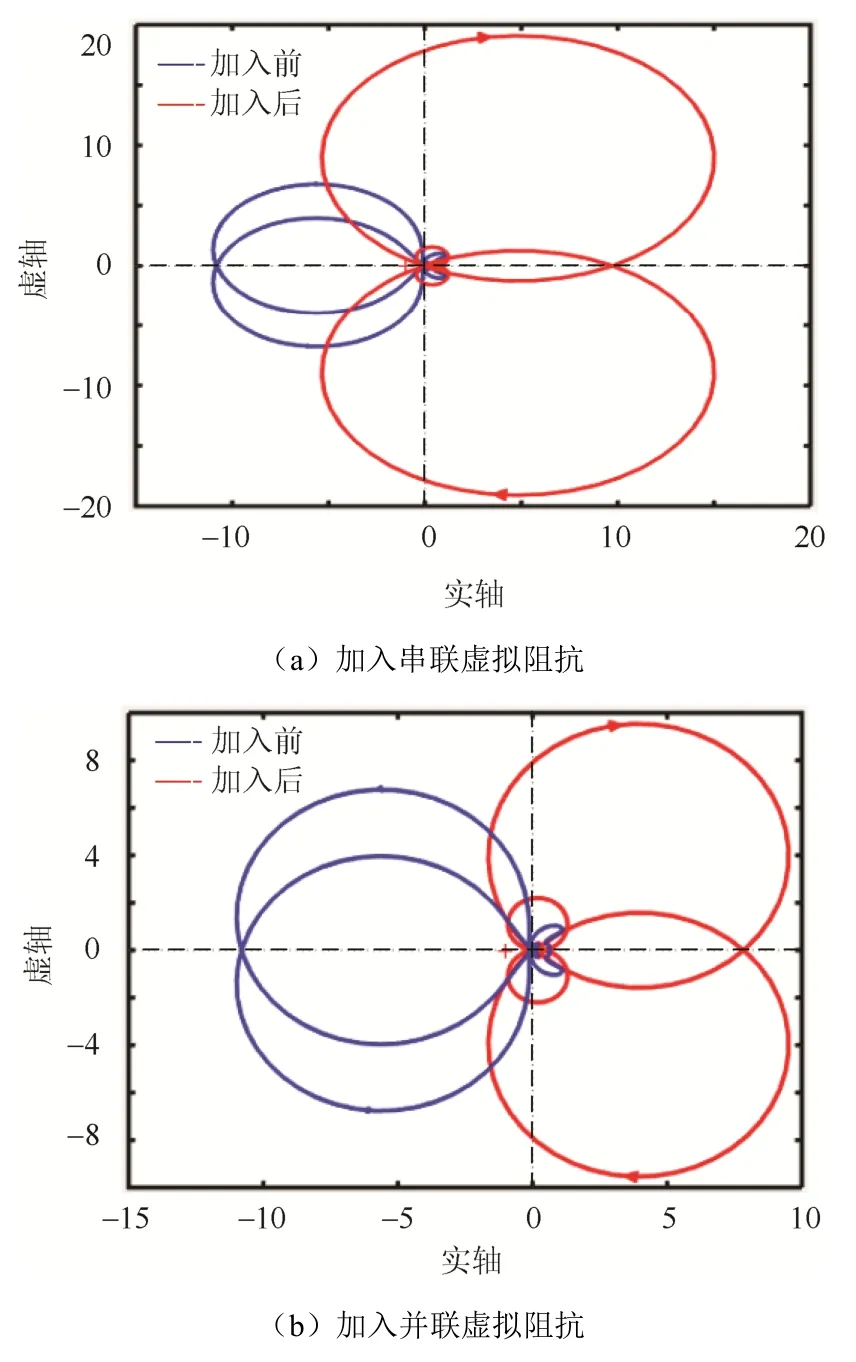
图11 弱电网下不同控制策略λqq的轨迹Fig. 11 The trajectories of different control strategies λqq under weak grid

图12为不同电网强度下，VSG并网电流仿真波形。在0～1.5 s时，Lg=3 mH；1.5 s时Lg变为15 mH。

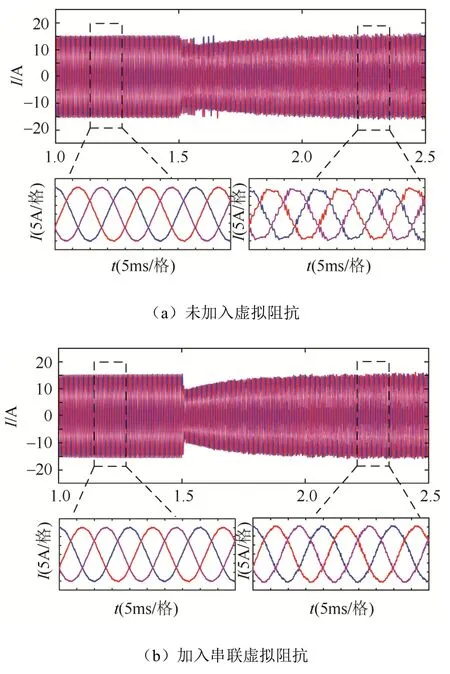
图12 不同控制策略下并网电流波形Fig. 12 Grid-connected current waveform under different control strategies

图12（a）为传统VSG控制下的并网电流波形，对比仿真结果得知，当Lg较小即为强电网时，VSG可以正常运行，当Lg变大，在弱电网环境下，电流中含有大量谐波，总谐波失真为9%，大于规定标准，仿真结果与图6所示结论一致。

图12（b）（c）分别为加入串联、并联虚拟阻抗后VSG的并网电流波形图。当电网阻抗由3 mH变为15 mH后，VSG都能稳定地工作，并且并网电流的总谐波失真低于5%。仿真结果与图11所示结论一致。

6 结论

本文深入研究了弱电网情况下 VSG运行状况，建立了系统输出阻抗模型，分析了不同电网强度与VSG稳定性之间的关系，对弱电网下VSG系统失去稳定的机理进行了阐明和总结。为此，提出采用串并联虚拟阻抗的方法进行改进，该方法不影响 VSG本身的动态性能，且大幅提高了VSG对弱电网的适应性，同时给新能源并网的技术理论提供了一定的参考，也为弱电网下VSG的控制提供了指导。