基于微波-电子康普顿背散射的环形正负电子对撞机束流能量测量方案*
董旭 黄永盛 唐光毅 陈姗红 司梅雨 张建勇
1) (河海大学理学院,南京 210098)
2) (中国科学院高能物理研究所,北京 100049)
环形正负电子对撞机(CEPC)束流能量的精确标定是希格斯粒子质量宽度、W/Z玻色子质量的精确测量, 从而精确检验标准模型的基本实验依据.基于此, 束流能量的误差控制要求在10–5水平.康普顿背散射方法是适用于百GeV高能电子对撞机束流能量高精度标定的测量方法.本文拟采用微波电子康普顿背散射后对散射光子能量的精确测量, 来反推CEPC束流能量, 理论预计精度可达到3 MeV左右.首先根据设计需求选定圆波导传输TM01模微波, 并求解该条件下的电磁场分布情况及坡印廷矢量.根据波导内光子分布传输情况提出设计思路简化计算的复杂程度, 结合高纯锗探测器灵敏度、同步辐射本底等限制条件联立方程求解符合设计要求的参数.使用最优的一组波导内径、微波波长、电子入射角数据求得微波功率为100 W时的微分散射截面对能量的导数及对撞亮度, 进一步求得15 MeV能量的散射光子数密度, 根据该能量下同步辐射光子数密度的大小分析了信噪比.理论上论证了该方案的可行性并讨论了该方案有待进一步研究的技术难点与问题.
1 引 言
欧洲核子中心的大型强子对撞机(LHC)于2012年发现希格斯粒子并将希格斯粒子质量的不确定度降低到160 MeV即mH= (125.18 ± 0.16)GeV[1].CEPC的目标之一是将不确定度降低到5.9 MeV, 其中束流能量是该方案的输入信号之一[2].因此, 希格斯粒子质量的不确定度也将取决于束流能量测量的不确定度, 所以需要设计一个束流能量测量系统使其满足系统的精度需求.
目前较为成熟的测量束流能量方法有很多, 例如: 共振去极化技术、激光康普顿背散射方法、激光康普顿背散射与光束跟踪方法等, 但已有测量方法中只有激光康普顿背散射方法能够达到测量的精度要求[3].1923年, Compton[4]发现当波长为λ0的X射线入射到碳靶上, 散射X射线波长与入射相比变长, 电子获得部分入射光子的能量, 该散射过程称为康普顿散射.电子-光子康普顿散射过程如下式[5]:

其中λθ为散射光子波长;θ是电子-光子对撞角;h为普朗克常数;m是电子的静止质量;c为光速.当电子能量大于150 MeV时, 电子将会把能量传给光子.对称分布的散射光子在实验室坐标系下观察会集中在电子入射方向的一个小角度内, 且散射光子的能量比入射光子的能量显著增大[5].该过程能量由电子转移到光子, 因此被称为康普顿背散射[6,7].康普顿背散射在1963年被提出用于高能光子产生[7], 啁啾脉冲放大技术和高电流、高亮度电子加速器的皮秒级太瓦激光器的迅速发展, 使得高能光子的产生在实验中得到成功[8−10].可调单色x/γ射线源, 其产生过程可以借助激光-高能电子散射来完成, 入射电子能量、入射光子能量、散射光子能量三者之间的关系如下式所示:

其中ωx为产生光子的能量;ω0为入射光子能量;γ为相对论因子可以代表电子能量的大小;ψ为微波光子与电子对撞角,a0与光子能量有关.
康普顿背散射方法目前已经应用在BEPCⅡ和VEPP得到很好的应用, 并到达了1.2 × 10–5的不确定度[11,12].该方法测量的束流能量均在10 GeV以下, 在测量120 GeV电子束时, 测量系统将受到同步辐射的极大影响.一方面同步辐射增加了本底数量影响精确度, 另一方面高能同步辐射光子还会对探测器造成很大破坏, 降低探测器使用寿命.由于高精度探测器的唯一选择是高纯锗探测器[13], 所以需要将散射光子最大能量控制在20 MeV以内, 同时为了避免低能区同步辐射光子产生的巨大本底, 散射光子最大能量还要控制在10 MeV以上.对散射光子最大能量的限制又带来了新的问题, 这将要求激光和高能电子束的对撞夹角约为0.04 rad, 由于对束流能量测量的精度要求是1 MeV, 所以角度的不确定度应在0.5 µrad左右.对夹角控制这么小的不确定度是相当困难的,同时如此小的对撞角将降低散射的亮度, 对撞亮度只有头对头对撞的万分之一, 由此将带来很大的统计误差[14].因此研究并解决在百GeV量级的加速器上实现如此精确的能量测量是国际公认的难题,具有重要的创新意义.
本研究基于康普顿背散射原理, 设计厘米波段的微波-电子康普顿背散射系统, 计算了100 W功率的微波源与高能电子束对撞产生的散射光子数密度, 并进一步计算信噪比.
与传统激光方案相比, 厘米波段的微波-电子康普顿背散射系统主要解决了康普顿背散射方法在百GeV量级的加速器束流能量测量中的夹角问题.在保证散射光子能量维持在探测器最佳工作范围内的前提下, 同时要求束流能量的不确定性小于1 MeV.通过计算可得若使用激光方案则对撞角过小, 此时激光与电子束对撞角的误差上限为4.2 × 10–7rad, 而CO2激光器的指向稳定性只有10–5rad, 不能满足精度要求.对此解决方案有二种: 一是针对现有激光器增加准直系统, 不过预期会相当严重的损失激光功率; 二是采用中红外光纤耦合激光器, 激光波长在2—5 µm, 指向稳定性在0.1 µrad, 可以满足要求.但是理论上需要2 km的真空管来传输激光, 才能达到较好的准直效果,使得该项导致的束流能量不确定度能在合理范围内.本文所使用的微波-电子康普顿背散射系统, 对撞角约为88°, 相比于激光方案, 对撞角的误差问题在微波方案中不攻自破.
本文参照激光-电子康普顿背散射的物理过程,在考虑不同波导的微波系统中光子分布情况后, 提出了CEPC束流能量测量的微波-电子康普顿背散射系统, 理论上论证了该方案的可行性, 为解决百GeV对撞机束流能量的精确测量提供了一种新方案, 并讨论了该方案有待进一步研究的技术难点与问题.
2 波导光场分布
2.1 波导及电磁波模式的选择
电磁波在场中传播, 频率不同则电磁能量传输问题的分析方式也不同.低频情况下, 不直接研究场的分布, 而用电路方程解决实际问题.高频情况中, 场的波动性愈加显著, 电流、电压的概念也失去其具体意义[15], 我们通过研究电磁场和电路上电荷电流的相互作用, 解出电磁场理解电磁能量传输的具体细节, 根据CEPC束流传播情况选择合适的波导和电磁波传播模式.
根据传输频率的不同, 电磁波的传输方式可以分为: 双线传输、同轴线传输和波导传输.其中, 双线传输适用于低频电力系统, 同轴线传输适用于中低频率传输.频率较高时, 介质中的热损耗及内导线的焦耳损耗变得严重, 此时需要用波导管代替同轴传输线.波导传输适用于微波波段, 因此本文设计讨论的方案中使用的电磁波传导方式为波导传播.
相比于矩形波导, 圆波导具有对称性强、边界条件单一等特点, 常用于毫米波的远距离通信、精密衰减器、微波谐振器等, 因此本方案中使用圆波导进行微波传输.对于圆波导如图1, 波导截面半径为a, 截面坐标采用极坐标(ρ,φ), 波导轴线为z轴, 电磁波传输方向为正向.若使电磁波能够在波导中进行传输, 必须选择合适的传输模式, 并且保证电磁波的波长小于截止波长λc.

图1 圆形波导及坐标系Fig.1.Circular waveguide and coordinate system.
根据电场和磁场在传播方向上的分量不同, 导行波波型大致分为三类: 横电磁波(TEM模)、TE模和TM模.TEM模是双导体结构传输系统的主模, 单导体结构的波导中不能传输TEM模.圆波导中的常用模式有TE11, TM01和TE01三种模式.TE11模尽管是圆波导中的主模, 却不宜作为传输模式.原因在于TE11模存在极化简并, 且由于圆波导加工中可能出现细微的不均匀性, 会使传输过程中电磁场的极化面会发生旋转.TE01模是一种无极化简并现象的轴对称模式, 只有Eφ,Hρ和Hz三个场分量, 壁电流分布只有φ分量, 因此不易设计束流入射孔.TM01模为轴对称或圆对称模,截止波长λc= 2.613a.因为m= 0, 所以TM01模无极化简并现象.TM01模只有Eφ,Hρ和Hz三个场分量, 由于模的场结构特点及轴对称性, 该模常用于雷达天线馈电系统的旋转铰链中.TM01模的壁电流分布只有z分量, 所以对于传输该模式的圆波导, 常常沿波导纵向开窄槽, 插入金属探针作为测量线使用.综合考虑以上三种传输波型在圆波导中的特点, 本方案使用TM01模作为微波的传导波型, 利用电磁场的结构特点及轴对称性便于分析计算电磁场与高能电子束的相互作用, 利用圆波导TM01模壁电流的分布特点可以在波导壁上开孔使CEPC高能电子束通过.
2.2 圆波导TM01模电磁场及能流分析
分析波导中的电磁波, 就是要得出导行电磁波沿轴向(纵向)的传播规律以及电磁场在横截面内的分布情况.通常可以使用纵向分量法的思想: 将导行系统中的电磁场矢量分解为纵向分量和横向分量, 由亥姆霍兹方程得出纵向分量满足的标量微分方程, 求解该标量微分方程, 得到纵向分量; 再根据麦克斯韦方程组, 找出横向分量与纵向分量之间的关系, 用纵向分量来表示横向分量.TM模满足Hz= 0,Ez(ρ,φ,z) =Ez(ρ,φ)e–jβj, 在极坐标中Ez(ρ,φ)的标量波动方程如(3)式, 应用分离变量法可以得到Ez的基本表达式如(4)式:

根据电磁场分量的纵横关系可以得到各个场分量的一般解(基本解的线性叠加)的表达式:

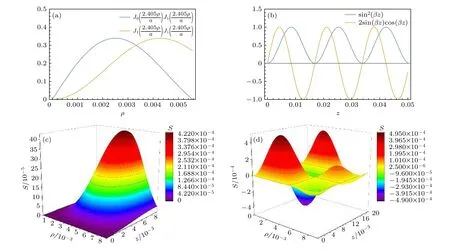
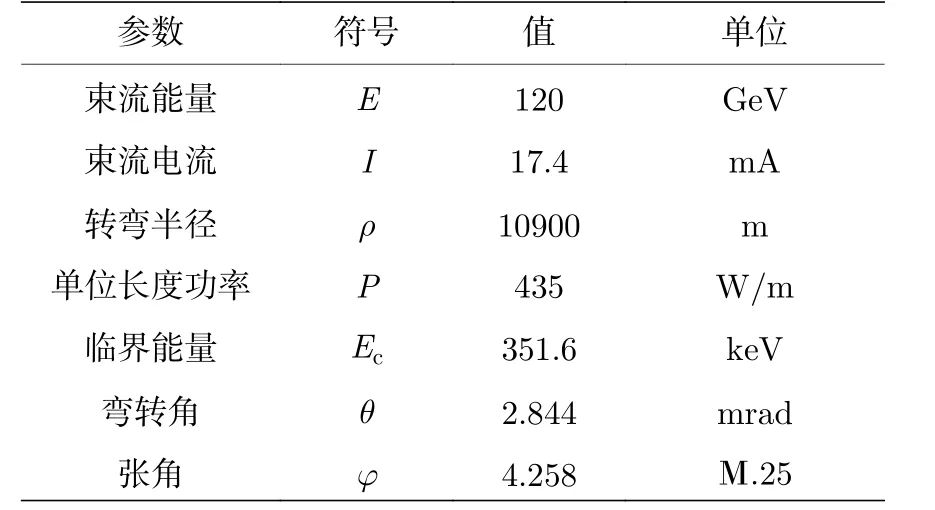
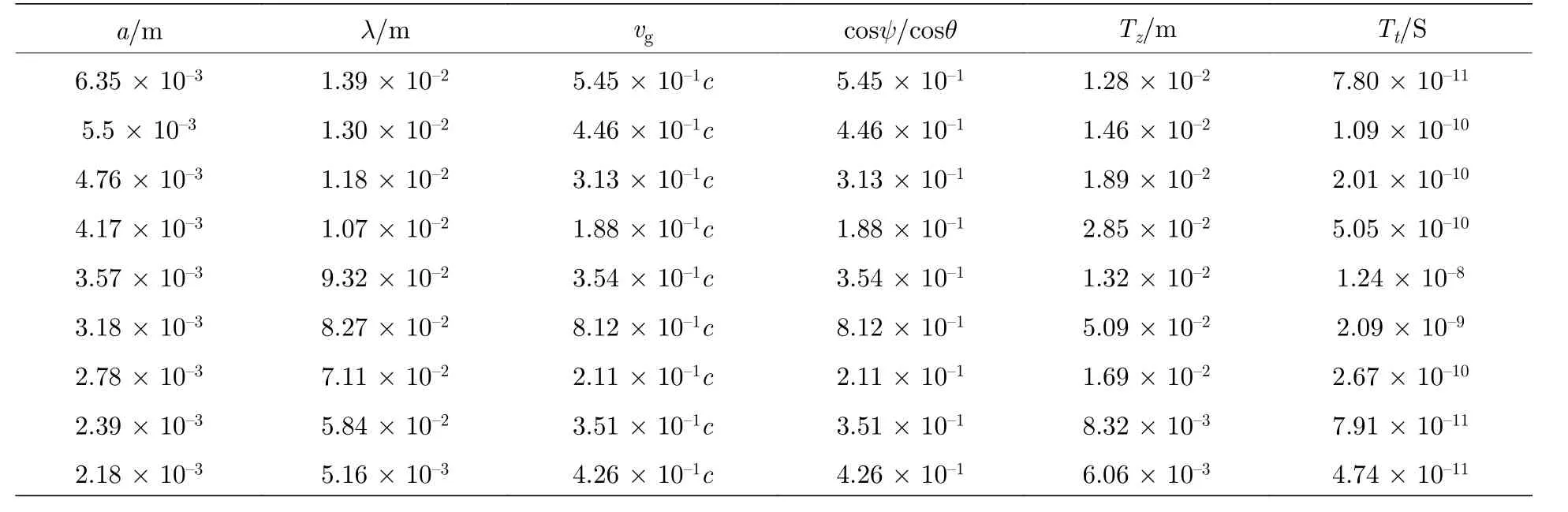
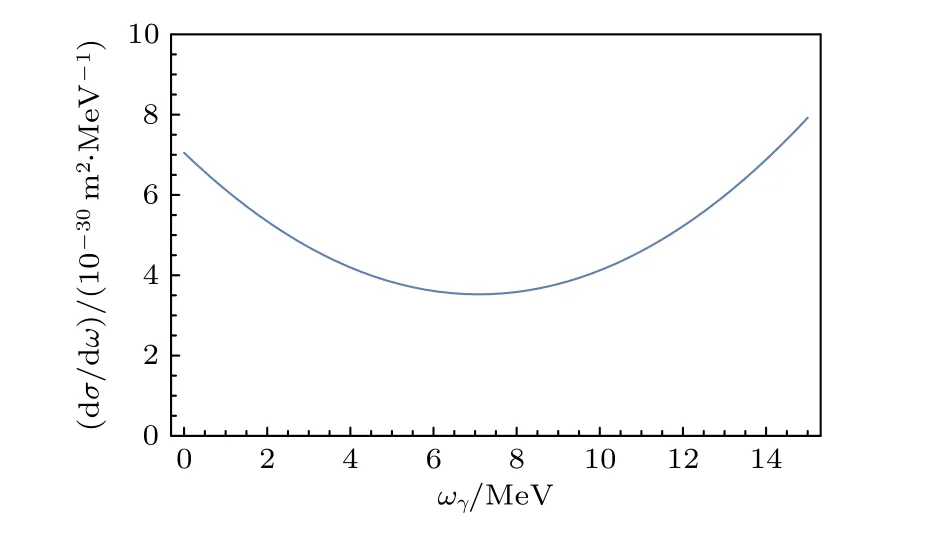
其中ρ为波导内一点到轴线的距离0 <ρ 由此可知, 圆波导TM01模电磁场中, 电场存在ρ和z分量, 磁场仅存在φ分量.则波导中的坡印廷矢量S=E×H=(Eρ+Ez)×Hφ, 将(9)式—(11)式代入得坡印廷矢量z,ρ分量的值为 由坡印廷矢量的结算结果可以分析能流沿坐标轴的变化情况, 坡印廷矢量的z,ρ分量仅与z,ρ坐标变化有关, 且坡印廷矢量z,ρ分量的常数项数量级基本一致, 因此在分析能流的变化情况时,可以仅考虑含坐标z,ρ的函数变化情况.由坡印廷矢量的结算结果可以得到Sz,Sρ沿z,ρ坐标在波导空间中的变化情况如图2(c)和图2(d)所示.分析(12)式前式可知: 坡印廷矢量的z分量Sz在平行于z轴方向上, 其大小沿z轴呈sin2(βz)函数周期分布, 沿z轴方向的周期情况如图2(b); 同一截面内,Sz大小与角度φ无关, 仅与ρ有关, 随着ρ由0增大至半径a,Sz的大小先由0增大至极值点后减小至非零值, 沿ρ方向的变化情况如图2(a).分析(12)式后式可知: 坡印廷矢量的ρ分量Sρ其大小沿z轴呈sin(βz)cos(βz)函数周期分布, 周期为与Sz相同, 沿z轴方向的周期情况如图2(b); 同一截面内,Sρ的大小与角度φ无关, 仅与ρ有关,随着ρ由0增大至半径a,Sρ的大小先增大再减小至0, 沿ρ方向的变化情况如图2(a). 图2 波导中坡印廷矢量变化情况 (a)各分量沿ρ方向变化情况; (b) 各分量沿z方向变化情况; (c)坡印廷矢量z分量在空间中的变化情况; (d) 坡印廷矢量ρ分量在空间中的变化情况Fig.2.Poynting vector variation in the waveguide: (a) The variations of each Poynting vector’s components along the ρ axis;(b) the variations of each Poynting vector’s components along the z axis; (c)variations of the z component of Poynting vector in space; (d) variations of the ρ component of Poynting vector in space. 对于在波导中的导行电磁波, 其波导轴线方向不是电磁波传输的真实方向[16].在垂直于z轴的截面上, 导行电磁波还存在驻波分量, 其平均坡印廷矢量为零, 但是瞬时坡印廷矢量不为零.因此, 波导中的导行电磁波实际上是曲折前进的, 并非沿着z直线传播.波导中光子的传播速度并不等于光速c和相速度, 而是等于群速度: 其中λ为微波波长;λc为电磁波传输的截止波长.由能流分布情况可知, 波导中的光子沿z轴方向周期分布, 每个周期内的光子沿z轴轴对称分布, 波导内的光子方向仅存在z方向和ρ方向并按照群速度向传导方向集体传输.由于电子束的长度相对于波导管的长度不能忽略, 电子束的速度相对于电磁波的群速度不可忽略, 因此若电子入射角固定,则与电子发生相互作用的光子分布随时间变化的情况较为复杂.所以可以考虑巧妙设置电子束入射夹角使电子速度的z分量与电磁波传输的群速度保持一致, 则当电子束与微波发生相互作用时, 电子束在微波坐标系下z方向保持不变, 仅在微波坐标系中固定横截面内与微波的光子发生散射, 这样就减小了计算的复杂程度.但在具体设计时, 由于需要考虑高纯锗探测器(HPGe Detector)灵敏度、同步辐射本底的存在等很多因素[17], 所以需要考虑较多限制条件, 我们试图在满足HPGe探测器灵敏度、总体设计误差需求的同时找到合适的波导规格、微波波段和对撞夹角. 束流测量是依靠测量微波-电子康普顿背散射光子的能量来反推电子束的能量来实现的(图3).BEPCⅡ采用激光-电子康普顿背散射的方法使束流能量的测量精度达到了2 × 10–5.该系统利用二氧化碳激光器产生的0.117 eV能量的光子与束流正碰, 电子束由二级磁铁偏转, 背散射产生的γ光子被HPGe探测器收集并标定能量[11].BEPCⅡ的物理取数计划主要集中在3到4.6 GeV之间, 散射γ光子的能量在4到9 MeV之间, 这个能量区间的光子可以由HPGe探测器精确测量.由于CEPC电子束能量较大, Higgs模式时电子束能量约120 GeV, 所以散射光子的能量必然比BEPCⅡ束流能量测量装置中的散射光子能量大得多, 为保证HPGe探测器工作在最佳探测能区, 需要选择合适的微波波长和对撞角保证散射光子能量在15到20 MeV之间[18]. 图3 微波法设计图Fig.3.Design drawings for microwave measurement method. 相对论性电子在磁场作用下沿弯曲轨道运动时, 在运动轨道切线方向上会发射电磁辐射, 称之为同步辐射[19].同时, 由于散射光子和同步辐射光子同时产生且速度相同, 所以同步辐射光子作为本底与散射光子同时到达探测器并被探测记录.在初步设计计算中, 暂未考虑同步辐射的屏蔽设计问题, 而是通过提高散射光子数与同步辐射光子数的比值即信噪比, 来实现满足束流标定系统的整体误差要求.由于同步辐射光子数随着能量增大而减小, 所以希望通过探测器测量散射光子最大能量来反推入射电子的能量.CEPC束流能量为120 GeV时同步辐射参数下表1[2]所列. 表1 CEPC同步辐射参数值Table 1.Parameters of CEPC synchrotron radiation. 为减小分析难度和计算复杂程度, 需设计电子束入射夹角使电子速度的z分量与电磁波传输的群速度保持一致, 即 c osθ=vg/ve≈vg/c, 其中θ为入射电子与波导的夹角,vg为微波群速度,ve为电子速度近似取光速c.满足该条件的电子束与微波发生相互作用时, 电子束在微波坐标系下z方向保持不变, 减小了计算的复杂程度.由(13)式知微波光子的群速度为圆波导TM01模单模传输需满足2.057a<λ<λc= 2.613a, 所以群速度vg≤ 0.617c. 在满足探测器精度要求的前提下, 为了得到较高的信噪比, 系统设计过程中要控制好各个参数使散射光子最大能量ωmax为15 MeV.散射光子最大能量计算入(2)式, 其中,a0与光子能量有关,近似取0.将ω=hυ代入得微波波长与对撞角之间的关系式: 其中h为普朗克常数, 当微波波长满足2.057a<λ< 2.613a即单模传输时, 需在满足以上两种限制条件的前提下分析角度、微波波长、群速度和波导尺寸四者之间的关系.联立以上两式使对撞角ψ=电子入射角θ得(15)式, 若方程式有解, 则该思路可行. 由图4可知, 满足以上两个限制条件的同时该方程组有解, 若使用标准圆形波导管, 则可以从中得到9组数据, 对应的波导半径a、微波波长λ等参数如表2所列. 表2 单模传输时微波-电子系统各参数值Table 2.Parameters of microwave-electronic system in single mode transmission. 图4 单模传输波长-内径解Fig.4.Solution of wavelength and inner diameter for single mode transmission. 表中Tz为坡印廷矢量轴向周期长度,Tt为能流传过坡印廷矢量轴向最小周期长度所用的时间.CEPC在Higgs模式运行时, 每束电子束团间隔时间为680 ns, 为保证系统的时间控制精度,Tt应接近百纳米量级, 故本方案采用第五组数据: 波导半径a= 3.5685 × 10–3m, 微波波长λ= 9.319 mm,电子入射夹角的余弦值cosθ= 0.035405.对撞角θ约为88°, 电子束轴向跨度Δz= 4.4 mm ×cosθ≈ 0.156 mm, 坡印廷矢量轴向周期长度Tz=13.1601 mm, Δz/Tz≈ 0.59%.由于电子所在能流面上所含ρ方向传播的光子占比很小, 故可以认为与电子束发生散射的微波光子均沿z传播. 决定对撞机产生事件能力的物理量用亮度L表示, 亮度是事件率dN/dt与被观测事件的散射截面σ之间的比例系数[20].所以微波光子与电子发生康普顿背散射每秒产生的散射光子数满足关系式(16)式, 两边对能量ω同时微分, 散射光子数密度表示为(17)式. 若考虑非极化电子束和非偏振光子的康普顿背散射, 且不考虑对剩余电子的自旋和散射光子的极化时, 微分散射截面的表达式如下[21]: 所以散射截面对能量的导数为(20)式, 将参数代入可知自变量为散射光子能量ωγ, 因此可以得到dσ/dω与散射光子能量ωγ之间的关系图如图5所示.从图5中可以看出, 当散射光子能量达到最大15 MeV时, dσ/dω的值最大, 此时对应的散射光子数密度也最大.代入参数得当散射光子最大能量为15 MeV时, dσ/dω= 7.92267 ×10–30m2·MeV–1 图5 散射光子不同能量对应的dσ/dωFig.5.Different energies of scattered photons corresponding to the dσ/dω. 为了从散射截面进一步得到康普顿背散射的事例数, 需要计算微波光子和电子散射的亮度, 这里考虑CEPC的单束电子束和连续微波相互作用的情况.由于微波中的光子传播方向与坡印廷矢量各个分量方向一致, 所以光子传播方向只有沿z轴方向和沿半径方向传播.为了计算方便, 仅计算一束电子束与微波光子相互作用的情况.假设该电子入射时, 入射电子束的中心位置恰好在坡印廷矢量z分量极大,ρ分量为0的能流截面上.并且不失一般性的认为, 电子束的粒子密度服从高斯分布, 微波光子分布与能流分布情况一致.分团束流与连续束团碰撞的亮度用以下表达式计算[22]: 式中,N1是微波光子数;N2是每束的电子数;B是束团数;f为回旋频率;c是光速;f1是微波光子的归一化分布函数;f2是电子束团的归一化分布函数;角度φ为光子电子的对撞角.在目前的计算中, 只分析一个电子束团与微波光子相互作用的情况, 所以B取为1, CEPC在Higgs模式下运行每束电子束团的电子数N2为15 × 1010[2], 回旋频率f等于电子速度除以CEPC储存环的周长, 其值约为3000, 描述微波光子分布的参数N1和归一化函数f1可由光子面密度σmic(ρ)表示.坡印廷矢量S表示的是单位时间通过垂直单位面积的能量, 单位是W/m2也可以写成J/(m2·s), 则单位时间通过单位垂直面积的光子数等于坡印廷矢量除以单个光子的能量:σmic(ρ)=S/(hν) , 单位是N/(m2·s),N是光子数.因为电子束的粒子密度服从高斯分布如(22)式, 所以电子束团与连续微波对撞的亮度写成(23)式的形式: 以上电子束团与连续微波对撞的亮度计算公式是在各自参考系中的形式, 在实际计算中需要统一微波和电子束的坐标系, 如图6.以波导Z轴为Z坐标, 电子路径与Z轴所在平面为X-Z平面, 从(xi,yi,zi) 坐标系到实验室坐标系 (x,y,z) 的变换坐标满足关系:x1=X,y1=Y,z1=Z;x2=Xcosθ−Zsinθ,y2=Y,z2=X/sinθ=Z/cosθ. 图6 电子束团、微波统一坐标系Fig.6.Unified coordinate system for electron beam cluster and microwave. 所以分布函数f2写成(24)式: 若微波功率为100 W, 将各参数代入(25)式,则亮度L100 W为2.81744 × 1036m–2·s–1.由(17)式光子数密度计算公式知: 散射光子数密度等于亮度乘散射截面对能量的导数, 当微波功率为100 W时, 散射光子数密度 此时同步辐射光子数密度为0.25 s–1·Me·V–1[18], 所以信噪比为8.92886 × 107符合系统整体误差的要求, 因此该方案可行.为了更好地说明微波方案的优势和可行性, 司梅雨等[23]对CEPC同步辐射、束流标定微波方案、波导微波结构及束流与微波之间的背散射进行了Geant4物理模拟, 模拟结果表明微波-电子康普顿背散射的方法在百GeV的大型对撞机中具有很好的应用前景. 通过分析微波光子与相对论电子的康普顿背散射过程, 提出了测量微波-电子康普顿背散射产生的高能光子的方法反推电子束能量的方法.分析了微波-电子散射系统的对撞条件、探测器精度限制和系统精度要求, 确定了内径为3.5685 × 10–3m圆波导TM01模微波传导的方案.考虑到波导中光子并不沿单一方向传播, 为减少电子束团与连续微波对撞过程的复杂程度, 通过理论计算合理设计电子入射夹角、微波波长和波导内径等参数, 保证电子速度的z分量与电磁波传输的群速度保持一致,使得电子束与微波光子相互作用的过程中, 电子束仅在微波坐标系中固定横截面内与微波的光子发生散射, 这样就减小了计算的复杂程度.最后在此设计的基础上计算了微波100 W时散射γ光子在15 MeV能量的产额, 通过计算散射光子数密度与同步辐射光子数密度的比值得到探测器数据的信噪比, 100 W微波产生的信噪比符合系统的误差要求, 论证了该方案的可行性.与BEPC等已有正负电子对撞机的束流能量测量系统相比, 该设计方案解决了激光-电子康普顿背散射法在百GeV量级对撞机中使用的理论困难. 本研究仅在理论上进行设计和计算, 并未考虑实际情况波导管接口处对微波的影响, 考虑到实际情况中微波在接口处分布可能较复杂且在传播中有辐射损耗, 所以有待于进一步实验验证.在计算微波光子与电子束发生康普顿背散射的光子产额时, 仅计算了单束电子与z方向传播光子的散射光子数密度, 其他电子束与光子散射的情况各不相同, 可以考虑之后使用统计方法计算出每分钟的光子产额, 使方案更有实用性.尽管探测100 W微波与电子相互作用的光子在高能区(大于15 MeV)能够得到较大的信噪比, 但是由于低能端同步辐射本底非常高, 低能端的噪声会对探测器造成影响,所以后期同步辐射的屏蔽工作也非常重要.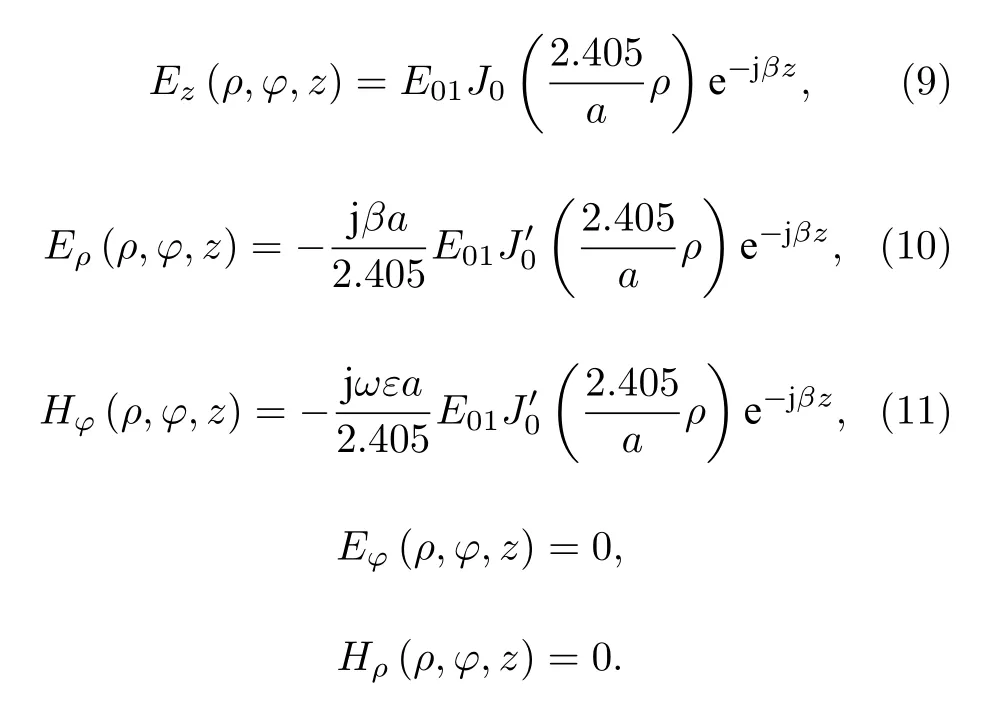
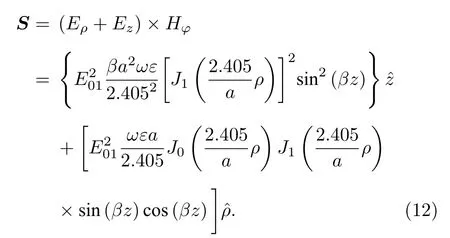
3 优化设计
3.1 设计思路


3.2 系统参数设定


3.3 散射光子数密度计算








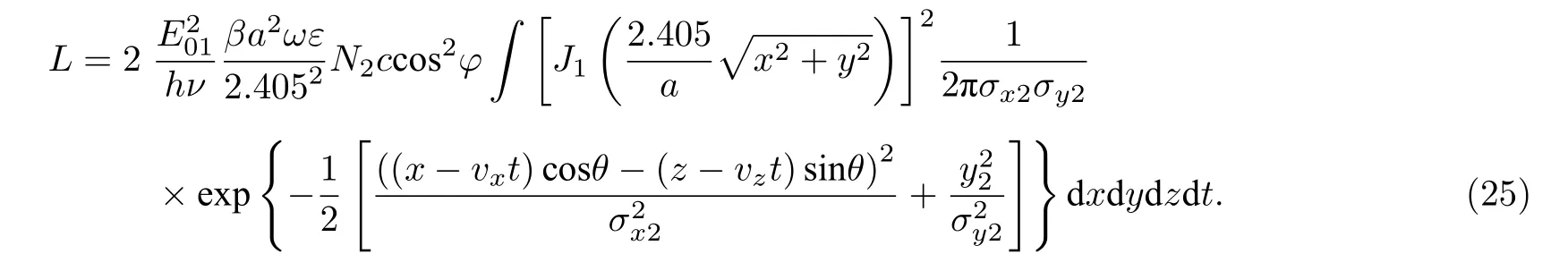

4 讨论与结论

