基于改进萤火虫算法优化SVM的滚动轴承故障诊断

常梦容 王海瑞 肖 杨 王椿晶 蒋朝云

（昆明理工大学信息工程与自动化学院）

滚动轴承作为一种十分重要的零部件，广泛应用于机械设备内部。 当今，滚动轴承的重要性越来越高，其工作精度和可靠度对设备的整体运行状态都有着关键性影响，同时对轴承故障诊断系统精度的要求越来越高。

支持向量机（SVM）参数的选择对整个诊断模型有至关重要的作用， 其惩罚因子C和核函数参数g的选择影响着SVM的诊断精度和泛化能力，好的核函数参数选择可以提高SVM分类的性能。对SVM核函数参数的选择， 前人做了许多研究，常 见 的 有 模 糊 聚 类［1］、网 格 搜 索 法［2］等 典 型 算 法以及蚁群算法［3］、鱼群算法［4］等智能算法。

在故障诊断中，故障诊断技术得到了广泛的研究与发展。 诊断方法主要有以下3类：基于解析模型的方法，如参数估计方法、状态估计方法及等价空间方法等；基于信号处理的方法，如EMD、傅里叶分析及小波分析等；基于知识推理的诊断方法，如模式识别、深度置信网络推理［5］等。 基于知识推理的诊断方法具备智能化方法和专家知识，可以提供一个可靠并且实用的系统。 然而，参数选择限制着这项技术的发展。 因此，笔者采用改进萤火虫算法（IFA）选取合适的SVM的惩罚因子C和核函数参数g， 构建IFA-SVM模型对滚动轴承故障进行诊断。

1 支持向量机

SVM作为一种强大的分类器，不仅可以作为二分类诊断模型，而且可以解决多分类问题。 它的目的是在特征空间中寻找到具有最大距离的一个超平面，从而将数据进行高效的分类，分为以下3种情况：

a. 当样本数据具有线性特征条件时，通常称之为硬间隔最大化，即在正例和负例之间分别寻找支持向量， 两个支持向量之间的距离称为间隔，要使这个间隔最大化，从而得到最佳的决策边界。

b. 当样本数据具有近似线性特征条件时，通常称之为软间隔最大化，即对于正确分类的实例点存在少量的噪声，引入松弛变量，并在实例点之间寻找支持向量，使支持向量之间的间隔达到最大化，最后学习到线性支持向量机。

c. 当样本数据不具有线性特征条件时，可在软间隔最大化的基础上引入核函数，使不可分的数据映射到高维空间中，即可实现分离。 此时将学习到一个非线性支持向量机的诊断模型。

给定一个特征空间上的训练数据集T=｛（x1，y1），（x2，y2），…，（xn，yn）｝，其中，xi为第i个特征向量，xi∈Rd；yi为类标记， 当它等于+1时为正例，等于-1时为负例。

当数据集线性可分时， 对于给定的数据集T和超平面ωTx+b=0，定义超平面关于样本点（xi，yi）的几何间隔li为：

超平面关于所有样本点的几何间隔的最小值l=minli，SVM模型的求解最大分割超平面问题可以表示为以下约束最优化问题：

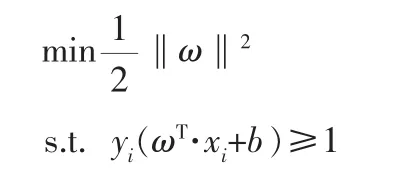
当几乎不存在完全线性可分的数据时，引入软间隔，即允许某些点不满足约束yi（ωT·xi+b）≥1，将原优化问题改写为：

其中ξi为松弛变量，ξi=max（0，1-yi（ω·xi+b））。当C增大时，ξi减小，ξi约等于0时，噪声少，超平面内侧相互移动，减小间隔距离，从而减少噪声，此时支持向量少；当C减小时，ξi增大，噪声多，上下超平面向外平移，加大间隔，从而增加噪声，支持向量多。

当样本数据不具有线性特征条件时，在软间隔的基础上引入核函数求解，通过把低维的非线性问题映射到高维空间中，使原本线性不可分的样本数据在高维空间中变得线性可分。

常见的核函数有：

因为RBF具备极强的高维映射能力， 所以在选取核函数时，RBF通常作为第一选择。RBF的原理是在固定xi的条件下， 使xj围绕xi以指数的方式进行衰减。 对于数据样本的标签，核函数把正例向正方向拉，把负例向负方向拉，从而使数据分离。 分离后的数据，具有较好的分割特性，因此可以选取较为合适的超平面使之分离，使得样本距超平面的距离最远。 RBF的指数项可以进行泰勒展开，展开式中的每一项，都可以被看作是在该维度上的样本分离。 故笔者以高斯核函数来进行讨论。 为了得到较高的分类精确度和良好的泛化能力，选择合适的核函数参数g和惩罚因子C对于整个模型较为重要：g作为核函数里面的重要参数决定了数据经过核函数处理后映射到新的特征空间的分布，影响了整个模型的训练与预测速度；惩罚因子C越大，对错误的容忍度越小，越容易发生过拟合，而C过小将导致容错率降低，分类准确度不高。

2 萤火虫算法

萤火虫算法（Firefly Algorithm，FA）属仿生群智能算法的一种，是模仿自然界中萤火虫在黑夜里发光来互相传递信息、互相吸引的算法［6］。

在FA算法中，可以将可行性的解用萤火虫的位置坐标来表示，适应度用萤火虫的亮度表示。萤火虫的位置与亮度成正比， 即亮度越高的萤火虫位置越好。在萤火虫之间，萤火虫总是向着比自己亮度更亮的萤火虫靠拢， 遵循着亮度越亮对其他萤火虫的吸引度越大的原则。在萤火虫飞行期间，传播介质会吸收一定的光，光被吸收后减弱，同时吸引度也减弱。当萤火虫之间的距离越来越远，光传播介质吸收的光越多即光越弱， 则吸引度也越小；当萤火虫之间的距离越来越近，光传播介质吸收的光越少即光越强，吸引度增大［7］。

萤火虫的相对荧光亮度I为：

其中，I0表示萤火虫距离为零（r=0）时的荧光亮度， 也是最亮萤火虫的亮度；γ表示光吸收系数，可设置为常数；rij表示萤火虫i和j之间的距离。

相互吸引度β的计算式如下：

其中，β0表示最大吸引度，即r=0（光源）处的吸引度。

萤火虫位置更新公式如下：

其中，xi、xj表示两个萤火虫的空间位置；α为步长因子；rand为［0，1］上服从均匀分布的随机因子；t为当前迭代次数。

3 改进的萤火虫算法

3.1 引入惯性权重的改进

线性惯性权重虽然容易理解， 实现简单，但并不是最好的递减策略，为此笔者将指数递减型惯性权重引入到位置更新公式中，在权重公式中加入随机扰动项进行自适应调整，公式如下：

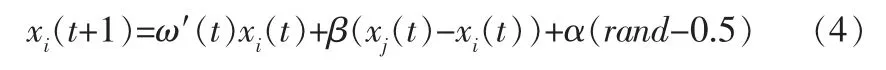
依据文献［8，9］，在萤火虫迭代初期，ω′（t）值较大， 萤火虫以较快的速度在群体之间进行搜索，把最亮萤火虫的大体位置确定下来，在此期间，由于ω′（t）较大，有利于增强全局寻优能力，同时局部搜索能力减弱，即在萤火虫的空间搜索过程中，之前的空间位置对当前的影响大。 相反在迭代后期，ω′（t）值较小，萤火虫在最亮萤火虫大体位置附近进入局部搜索，此时萤火虫的局部搜索能力增强，全局搜索能力减弱。 引入指数型惯性权重改进的方法，可以避免萤火虫飞行速度过快，错过极值点或在极值点反复振荡。

笔者在对萤火虫进行指数型惯性权重改进之前，借鉴了非线性递减惯性权重的思路［10］，为了让萤火虫前期能较快地进行全局搜索，后期也能快速进入局部搜索，并提高局部搜索能力。 惯性权重指数型递减策略可以达到上述目的，权重公式如下：

其 中，ω′max=0.8，ω′min=0.2，T=200，rand 是［0，1］之间的随机数，使得ω′（t）∈（0，1）。

3.2 吸引度改进策略

由于基本FA吸引度是指数型的，增加了计算量并且运算效率低，因此首先将基本FA指数型改为分式型，可以减少计算量，运算效率也会提高，同时利用最小吸引度增加每个萤火虫之间的吸引度，公式如下：

IFA算法流程如图1所示，具体说明如下：

图1 IFA算法流程

a. 初始化各参数，萤火虫初始种群的规模n、光强吸收系数γ、最大吸引度β0、步长因子α及最大迭代次数等参数；

b. 随机初始化萤火虫的位置，计算萤火虫的目标函数值作为各自最大荧光亮度I0；

c. 计算种群中各个体的最大荧光亮度和各自的吸引度值；

d. 依据式（5）更新权重；

e. 根据步骤c计算出来的荧光亮度和吸引度来更新个体位置，即向荧光亮度比自己更亮的个体移动；

f. 重新计算各个体的荧光亮度和吸引度，再更新萤火虫的位置；

g. 判断是否达到最大迭代次数或精度；

h. 输出全局极值点和最优个体值。

4 实验验证

4.1 实验准备和特征提取

为了验证IFA-SVM模型在轴承故障诊断中的有效性。 利用凯斯西储大学的滚动轴承故障诊断公开实验数据进行验证。 选取滚动轴承的10种状态：正常、内圈故障（点蚀直径0.177 8mm）、内圈故障（点蚀直径0.355 6mm）、内圈故障（点蚀直径0.533 4mm）、滚珠故障（点蚀直径0.177 8mm）、滚珠故障（点蚀直径0.355 6mm），滚珠故障（点蚀直径0.533 4mm）、外圈故障（点蚀直径0.177 8mm中心方向）、外圈故障（点蚀直径0.355 6mm中心方向）、外圈故障（点蚀直径0.533 4mm中心方向）。

电机转速为1 750r/min， 采样频率为12kHz。本实验选取1 000个数据点作为一组数据样本，其中700个作为训练样本，300个作为测试样本，具体的数据详细介绍见表1。

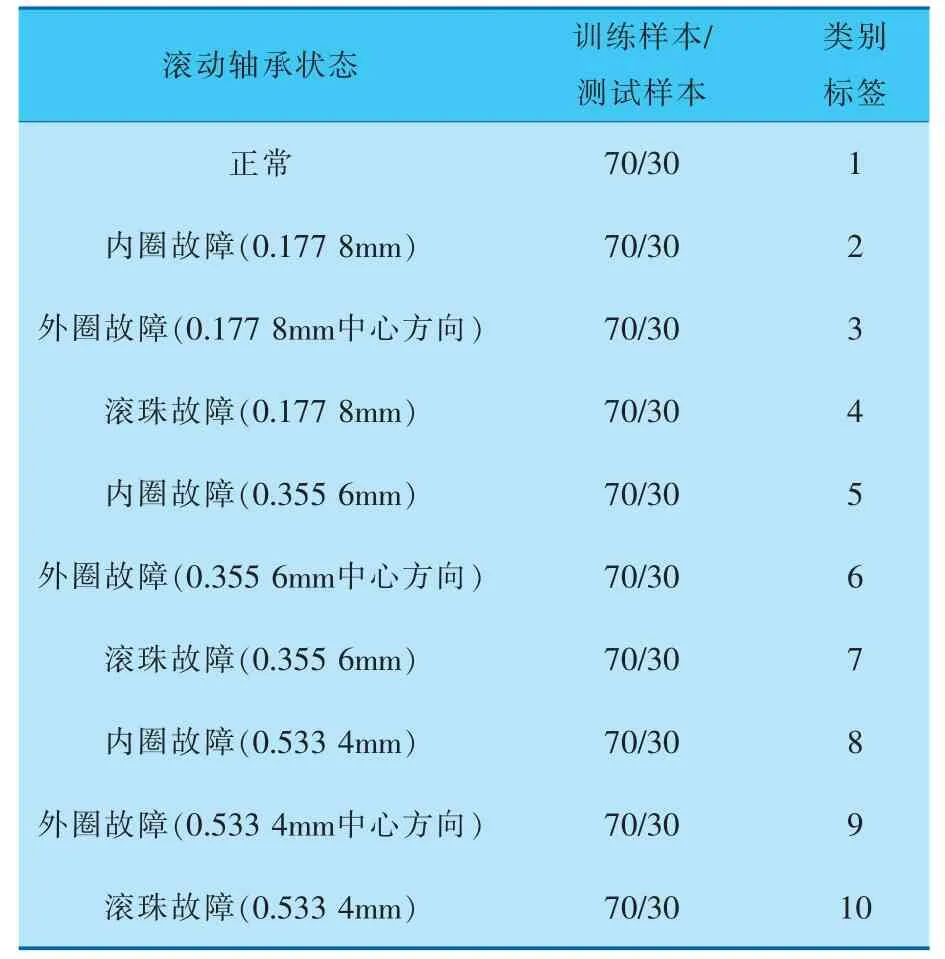
表1 滚动轴承状态描述

在本实验中首先依次提取标准差、 有效度、歪度、峭度、峰值、峰峰值、波形因数、脉冲因素、峰值因素和裕度，共10个特征类型。 其次对数据进行归一化处理，接着输入到基本FA-SVM、基本SVM、IFA-SVM中进行分类并对比分析。本实验在MATLAB R2020，Windows 10系统下进行测试，萤火虫数量n=20，最大迭代次数为100，α=0.25，βmin=0.2，γ=1。

4.2 实验结果分析

首先将训练样本输入IFA-SVM中，并利用IFA算法优秀的寻优能力， 找到最佳核函数参数g和惩罚因子C， 再将核函数参数g和惩罚因子C设定到SVM模型中，最后经过分类和训练得到较好的结果。

为了验证本方法的有效性， 选择SVM、FASVM进行比较。先进行基本SVM的分类，设置SVM的C=2、g=0.4， 然后代入SVM中进行分类和测试，得到的最高准确率为91.66%， 最低准确率为84.34%， 平均准确率为86.9%。 接着进行未改进FA-SVM的测试，得到C=96.4892，g=15.7697，最高准确率为90.67%，最低准确率为88.33%，平均准确率为89.4%（表2），可以看出虽然SVM最高准确率比FA-SVM高，但是FA-SVM无论从平均准确率还是最低准确率的角度分析，都比SVM模型的准确率高， 说明FA算法在一定程度上可以优化SVM，但是优化效果不佳。

表2 3种诊断模型的诊断准确率 %

虽然FA算法在一定程度上可以优化SVM，但是由于优化效果不佳，因此采取对FA进行改进的实验对比，以此证实IFA算法的优越性。 对700组轴承数据利用IFA-SVM模型进行训练， 得到最佳的C=4.2535，最佳的g=0.0553。再将参数g和C代入IFA-SVM模型中， 将300组测试样本进行分类，采用IFA-SVM得到的仿真结果准确率见表2，可以看出IFA-SVM最高准确率为95.00%，最低准确率为92.67%， 平均准确率为93.5%， 无论从最高准确率、最低准确率还是平均准确率角度分析，均高于SVM和FA-SVM，说明IFA-SVM优化效果显著。

图2是3种算法分别做5次实验的识别准确率比较，可以看出，IFA-SVM的准确率一直高于SVM和FA-SVM，并且准确率呈上升趋势，证实了IFASVM的性能。

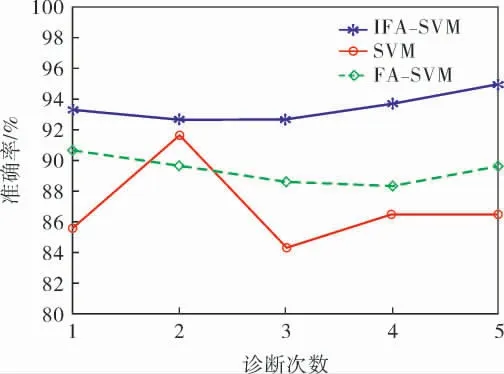
图2 3种诊断模型识别准确率比较

进一步分析模型的分类结果和模型对哪一类数据分类效果较差。 使用混淆矩阵分别对每一类数据进行错误分类统计（图3），从图3中可以看出，第1、2、3、4、6、7、8、9、10类故障都得到了较好的训练结果， 而第5类故障 （内圈故障（0.355 6mm））仅有47%的识别准确率，说明模型对于该类故障不能进行较好地识别。

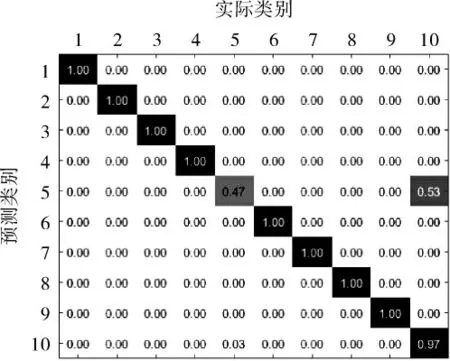
图3 混淆矩阵

对3种模型进行对比实验， 图4为3种诊断模型的实际测试集分类和预测测试集分类结果的对比，可以分析得出SVM正确分类253个，错误分类47个；FA-SVM正确分类274个，错误分类26个；IFA-SVM正确分类284个，错误分类16个。 实验结果表明：IFA-SVM在很大程度上提高了滚动轴承故障诊断的准确率和分类效果，具有很好的工程应用价值。

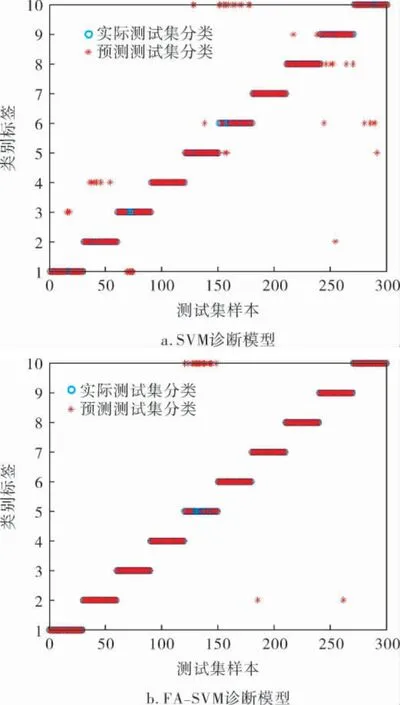
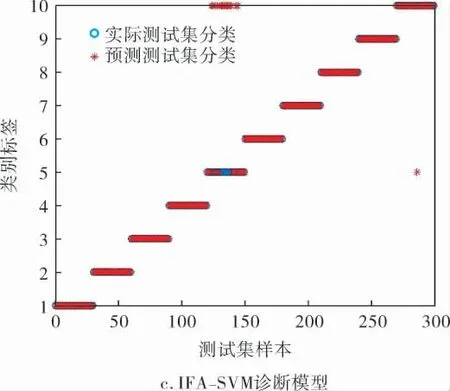
图4 3种诊断模型实际与预测测试集分类比较

5 结束语

基本萤火虫算法容易过早陷入局部最优值、收敛速度慢且求解精度低，笔者提出一种基于动态惯性权重的FA-SVM故障诊断方法。 该方法在位置更新中加入惯性权重，同时在权重公式中加入随机扰动项进行自适应调整。 通过对比SVM、FA-SVM和IFA-SVM这3种模型的最高准确率、最低准确率、平均准确率以及诊断模型实际与预测测试集分类， 验证了IFA-SVM模型准确率高且分类效果好。 通过混淆矩阵分析得出IFA-SVM模型不能对特定的类别做出较好的分类。