基于改进随机森林算法的企业破产预测研究
■ 张康林 叶春明
上海理工大学管理学院 上海 200093
0 引言
2020年,新冠肺炎疫情的爆发使世界经济遭受沉重打击,许多企业也陷入了财务困境,相比于从前,它们破产风险剧烈增加,而企业是全球经济的重要组成部分,也是经济增长的基础,更是社会进步的重要推动力,对公司进行破产预测变得愈加重要[1]。同时,预测公司未来的命运,一直都是金融机构、基金经理、贷款人、政府和经济利益相关者关注的重点,破产预测的结果不仅能够帮助投资者做出有效决策,还能提前警示公司管理层,帮助管理层提前实施保护措施,从而降低公司破产风险。
截止到2020年,企业破产预测研究主要从两个角度出发,分别是破产预测指标的选取和破产预测模型的选取。
对于破产预测指标,1966年,Beaver 首次提出在企业破产预测研究中,财务指标具有很高的研究价值[2]。自此,许多学者也都开始使用企业财务指标进行企业破产预测相关研究[3-4],比如Tian 等人[5]使用留存收益/总资产、总负债/总资产和流动负债/销售额3个财务比率指标构建了日本企业破产预测模型,并取得了良好的预测结果。但由于企业破产数据集具有高维的特性,影响模型分类性能,需要进行特征提取,文献[5]使用了自适应LASSO 方法筛选出了3 个财务指标作为预测变量;Kou等人[6]提出了一种两阶段多对象特征选择算法进行了特征提取,在中小企业破产预测模型中实现了类似的分类性能;Liang 等人[7]还使用3 种滤波器和两种基于包装的方法对财务比率和公司治理指标进行了特征选择,通过对比预测性能,确定了最佳特征选择方法。
对于破产预测模型,目前相关技术包括两大类,分别是模式识别和机器学习。1968年,Altman[8]就根据会计知识,对22 个财务比率进行了线性鉴别分析,利用其中5 个财务比率构建了预测模型。随后,使用逻辑回归[9]、神经网络[10]、支持向量机[11]来构建公司破产预测模型的研究相继被提出,比如杨毓等人[12]使用了支持向量机构建了商业银行破产预测模型,与反向神经网络模型对比发现,支持向量机具有更好的分类性能。但由于企业破产预测研究中,数据集存在类不平衡问题,决策树、K-最近邻域分类、支持向量机和多层感知机等传统分类器主要关注多数类而忽略了少数类,而解决不平衡数据的分类问题,集成学习方法具有更好的鲁棒性和泛化能力[13],Le等人[14]基于不平衡的KRBDS 数据集,使用改进的极端梯度提升器与最先进的破产预测机器学习方法对比发现,所提出的方法更优;还有Shen 等人[15]在研究中发现随机森林分类器在不平衡数据分类任务中优于决策树、支持向量机、贝叶斯等分类模型。
综上分析,本文选取的破产预测模型指标为财务比率,选取的破产预测模型为随机森林。
由于企业破产数据集具有高维不平衡的特性,因此会降低具有破产风险企业的预测精度。而针对这一问题,不同学者分别从样本处理、变量选择以及预测器选择3 个方面进行优化。Gruszczynski[16]从不平衡样本方面进行研究,探讨类别不平衡对破产模型预测精度的影响,Wagenmans[17]使用逻辑回归、神经网络、随机森林以及决策树四个模型进行破产预测研究,对比模型预测结果,筛选出最佳预测模型,Tuong 等人[18]使用基于GPU的极端梯度提升机器,提出了一种gXGBS_hist 算法,在不平衡的韩国破产数据集上进行实验,最终能够提高模型性能并加快模型处理时间,这些研究者都仅仅只从单方面进行优化。Choi 等人[19]先进行了数据平衡化处理,再通过模型组合对建筑行业承包商的财务困境进行了预测,Tuong 等人[20]使用了实例硬度阈值(IHT)的采样方法删除了多数类中具有较大IHT 值的噪声实例,然后提出了一种基于集群的提升算法CBoost并用于破产预测,而这些学者是同时结合了数据层面与模型层面的相关算法进行了破产预测研究。Philippe[21]首先对包含150个变量的不平衡破产数据集进行变量选择,最后再通过一系列的模型设计构建了最佳破产预测模型,采用了特征处理与模型设计相结合的流程;同样,Kim等人[22]从代表了公司盈利能力、稳定性、活跃性和生产率的111个财务比率中筛选出了53个显著比率作为模型特征,并提出了一种DD-SVM进行企业破产预测的混合方法。
通过对上述研究梳理可知,少有研究同时采用了特征提取、类平衡化、模型设计这3 种方法。本文将此3 种方法进行了结合,弥补了这一方面的不足。并在指标选取方面,对文献[23]的Pearson 相关系数特征提取规则进行了相应的改进;在模型构建方面,首先进行数据平衡化处理,然后对随机森林模型进行改进。实验结果表明,本文提出的研究方法在企业破产预测方面效果更加显著。
1 相关算法改进
1.1 Pearson相关系数特征提取规则
Pearson 相关系数(Pearson Correlation Coefficient)是用来衡量两个数据集合是否在一条线上面,从而用来衡量定距变量间的线性关系,相关系数的大小表示两个变量属性fi与fj之间的线性相关程度,其计算公式如(1)所示:

公式(1)中,c的取值范围为[-1,1],c=-1 时表示fi与fj完全负相关,c在(-1,0)的范围内时表示fi与fj为负相关关系,c=0 是说明fi与fj完全不相关,c在(0,1)的范围内时说明fi与fj为正相关关系,c=1 说明fi与fj完全正相关,c绝对值越大越接近1时,说明相关性越强,也就是说它们之间包含较多相似的信息,对于分类器来说属于冗余变量,需要删除其一。表1为c绝对值的不同取值范围对应的fi与fj相关强度。

表1 c绝对值的不同取值范围对应的相关强度
本文的Pearson相关系数特征提取规则如下:
1.计算属性与属性之间的相关系数以及属性与类别标签之间的相关系数;
2.依次判断两两属性之间的相关系数是否大于等于0.8,如果是,则跳到第3步;
3.比较两个属性与类别标签之间的相关系数大小,选择删除其中相关系数更小的属性,而不是随机选择删除其一;
4.直至所有属性两两之间的相关系数小于0.8,停止。否则返回第2步。
1.2 改进的随机森林算法
Breiman[24]提出的随机森林模型是基于决策树方法构建的集成机器学习工具,旨在提高决策树的性能。传统随机森林的算法步骤如下:
1.令收集来的数据集为D={xil,xi2,…,xin,yi}(i∈[l,m]),m为样本数,特征数为N,采用Bootstrap 方法从D中抽取D1个样本作为训练集。
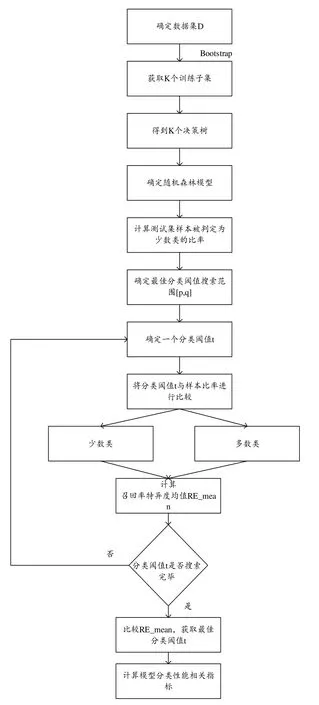
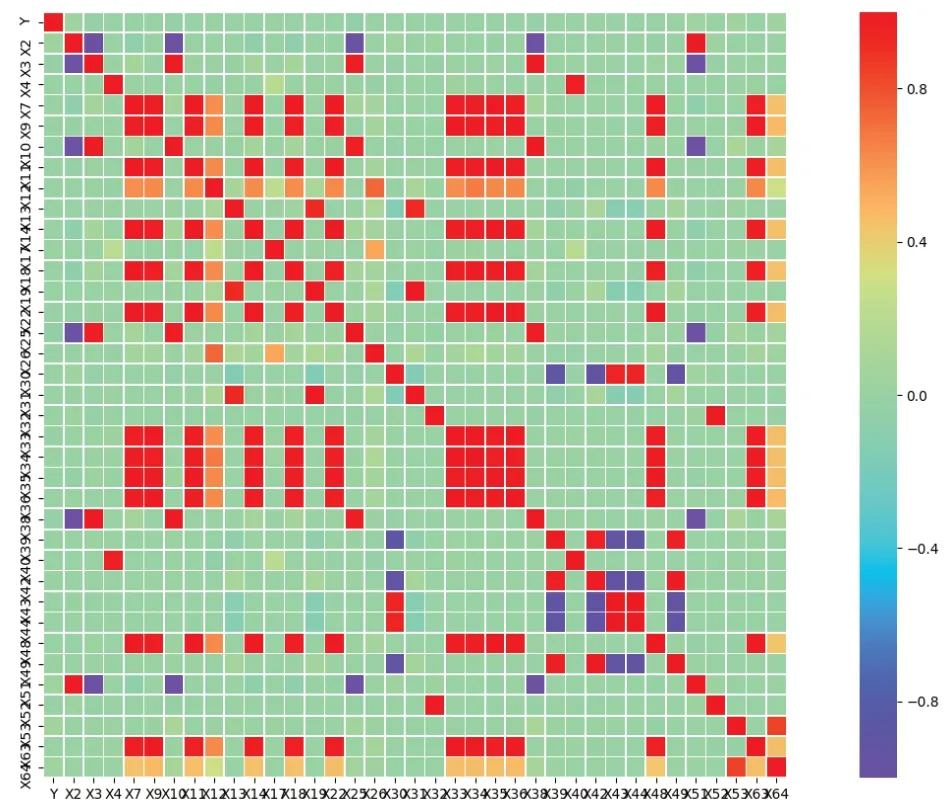
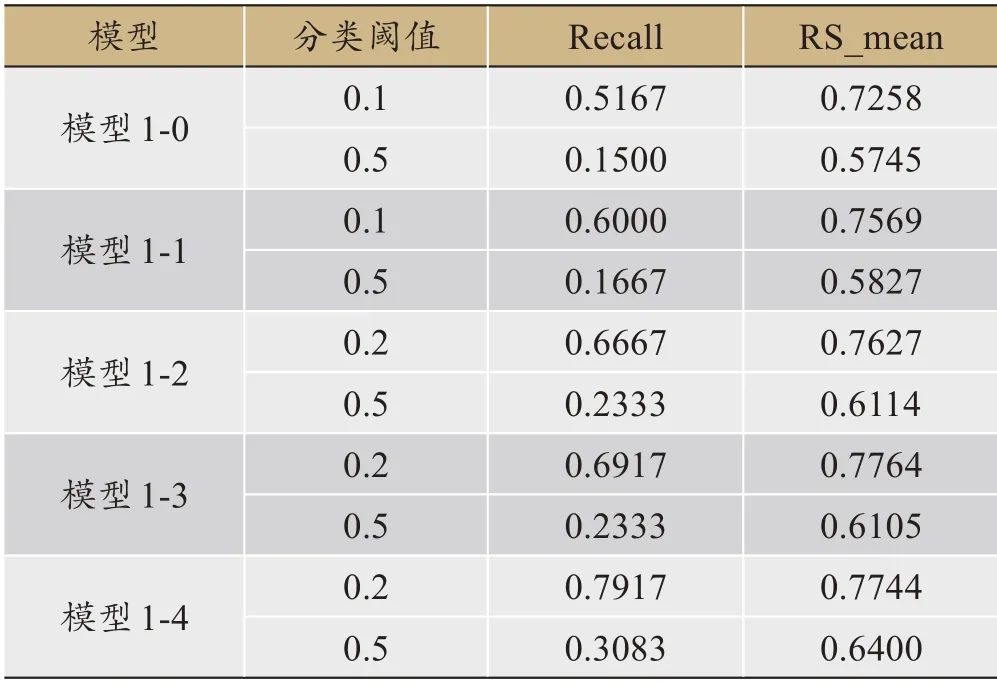
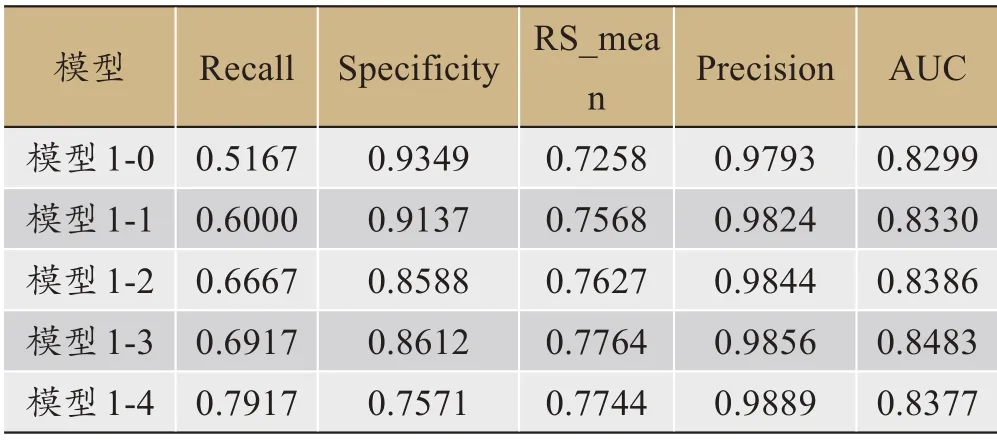
2.使用第1 步得来的数据集D1={xil,xi2,…,xik,yi}(i∈[l,m])(其中k< 3.重复1 和2 两个步骤K次,得到K个决策树,组合K个决策树得到随机森林。 4.使用测试集进入随机森林的预测阶段,预测公式可通过式(2)进行表示。 (2)式中,H(x)为最后分类结果,hi(x)为第i棵决策树的分类结果,Y为类别标签,I为简单投票法。 在二分类实验中,所谓的简单投票法就是K 个决策树有K 个分类结果,如果该样本被分类为A 类的结果数占比大于0.5,则可以判定该样本属于A 类,反之属于B类。可以看到,其分类阈值为0.5,但是在企业破产预测研究中,由于存在类不平衡问题,应该对分类阈值进行调整,找到最佳分类阈值,提高模型整体的分类性能。 所以本文将从随机森林算法的第4步开始进行如下改进: 4.计算测试集样本Dt={x1,x2,...,xz}在随机森林模型中被判定为少数类的比率R=[rx1,rx2,...,rxz]。 5.确定最佳分类阈值搜索范围T=[p,q],0 6.在T中确定一个分类阈值t,依次将样本xz的比率rxz与t进行比较,若大于t,则将其判定为少数类,反之判定为多数类。 7.基于分类阈值t得到一个测试集样本的分类结果,再根据分类结果计算召回率特异度均值RE_meant并保留,计算公式如式(3)所示;返回第6 步,直至范围内所有分类阈值被判定完毕。 8.比较每一个分类阈值对应的召回率特异度均值大小,最大召回率特异度均值对应的分类阈值即为所求。 9.根据确定的最佳分类阈值计算模型的分类性能相关指标,判断最终模型的好坏。 算法流程图如图1所示。 图1 改进的随机森林算法 本文所有实验都是在系统WIN10、1TB+128G(SSD)的硬盘、INTEL 酷睿I7-6700Q 的CPU 和内存4GB 的PC机上通过python3.7 版本完成。实验流程图如图2所示。 图2 实验流程图 本文所使用的数据来源于全球新兴市场信息的数据库,共10173个企业,其中400个为在2013年破产的企业,9773 个为在2013年未破产的企业,从图3可以明显看出,数据存在类别不平衡问题。 图3 企业破产数据集类别分布图 每一个样本共包含64 个属性以及1 个预测类别,特征含义如表2所示,属性均来自于公司2008年的财务报表。 表2 企业破产预测数据集特征构成 由于所收集到的数据集存在缺失值且属性单位不一致,需要进行缺失值处理和归一化处理。缺失值均属于连续值,所以用该列的平均值进行填充;归一化处理计算公式如(3)所示。 式(3)中,X′i,j表示归一化处理后的数据,Xi,j表示原始数据,Xmin表示第j 列中的最小数,Xmax表示第j 列中的最大数。 根据本文提出的Pearson 相关系数特征提取规则,首先计算属性与属性之间的相关系数以及属性与类别标签之间的相关系数,并用相关系数热力图进行了展示。图4为保留下来的指标相关性热力图,图5为已删除的指标相关性热力图 从图4和图5可以得出保留下来的特征分别是X1,X5,X6,X8,X15,X16,X20,X21,X23,X24,X27,X28,X29,X37,X41,X45,X46,X47,X50,X54,X55,X56,X57,X58,X59,X60,X61,X62,共28个。 图4 保留下来的指标相关性热力图 图5 已删除的指标相关性热力图 首先进行数据集的划分,70%为训练集,30%为测试集,训练集和测试集中两类样本数量如表3所示。 表3 训练集和测试集中两类样本数量 针对类别不平衡问题,本文使用了现常用的3 种处理方法。第一是SMOTE 过采样[25],它通过生成合成样本而不是复制少数类的样本来对少数类进行过采样,包括3个步骤,首先选择原始样本中的K最近个样本,然后将原始样本与所选的K 最近个样本之间的距离乘以从0到1 的随机数,最后将相乘距离的平均值与原始样本相加,生成新样本,重复3 个步骤,直至少数类和多数类样本平衡;第二个是SMOTETomek Links 混合采样法,它是将SMOTE 和Tomek Links两种算法进行结合,首先通过SMOTE 算法对数据集中少数类样本进行合成,然后通过Tomek Links 算法去清洗数据集,删除采样后数据集的中的Tomek Links 对,Tomek Links 对的寻找过程如下:首先假设两个样本点x,y,样本x 取自于少数类样本集,样本y取自于多数类样本集,然后计算两个样本点的欧式距离,并记为d(x,y),最后如果不存在第3 个样本点z,使得d(x,z) 本文将SMOTE中的样本近邻数K 统一规定为5,最终经3种平衡化方法处理后的数据集如表4所示。 表4 经四种平衡化方法处理后的样本数分布表 本文研究的是一个二分类问题,所以将会采用召回率(Recall)、特异度(Specificity)、召回率特异度均值(RS_mean)、精准率(Precision)以及AUC 值,计算公式为(5)至(7)所示。 TN真阴性为多数类样本被预测为未破产的实例数,FP假阳性为多数类样本被预测为破产的实例数,FN假阴性为少数类样本被预测为未破产的实例数,TP真阳性为少数类样本被预测为破产的实例数。召回率代表所有破产企业实例中预测为破产的实例比列,用来评价少数类样本分类准确率;特异度代表所有未破产企业实例中预测为未破产的实例比列,用来评价多数类样本分类准确率;召回率特异度均值用来衡量正类与负类被预测正确的一个综合比例,用于本文分类阈值的选择;精准率代表了所有正确预测为企业破产的实例数占所有预测为企业破产实例数的百分比。 2.5.1 随机森林参数选择 随机森林模型的预测性能取决于两个参数,分别是决策树的数量和决策树的深度。本文使用网格搜索法对以上两个参数进行选择,决策树的数量搜索范围为range(10,101,10),决策树的深度搜索范围为range(3,21)。5种训练集下随机森林模型的两个参数的最终取值如表5所示。 表5 5种训练集下随机森林模型两个参数的最终取值 2.5.2 分类阈值的选择 为了进一步提升对少数类的预测准确率以及模型的整体分类性能,本文考虑将其阈值进行改变,观察其对预测结果的影响,阈值的选择有[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]九个值。 模型1-0、1-1、1-2、1-3、1-4 的召回率、特异度、召回率特异度均值变化曲线分别如图6~10所示。 以召回率特异度均值为评价标准,RS_mean 值越大,模型分类性能越好。所以可以从图6~10 得出,模型1-0 与1-1 的最佳分类阈值为0.1,模型1-2、1-3、1-4 的最佳分类阈值为0.2。最佳分类阈值与分类阈值为0.5的结果对比如表6所示。 图6 模型1-0召回率、特异度、召回率特异度均值变化曲线 图7 模型1-1召回率、特异度、召回率特异度均值变化曲线 图8 模型1-2召回率、特异度、召回率特异度均值变化曲线 图9 模型1-3召回率、特异度、召回率特异度均值变化曲线 图10 模型1-4召回率、特异度、召回率特异度均值变化曲线 可以从表6看出,模型1-0 在分类阈值为0.1 时,Re‐call 比阈值为0.5 时高36.67%,RS_mean 比阈值为0.5 时高15.13%;模型1-1 在分类阈值为0.1 时,Recall 比阈值为0.5 时高43.33%,RS_mean 比阈值为0.5 时高17.42%;模型1-2在分类阈值为0.2 时,Recall 比阈值为0.5 时高43.34%,RS_mean 比阈值为0.5 时高15.13%;模型1-3 在分类阈值为0.2 时,Recall 比阈值为0.5 时高45.84%,RS_mean比阈值为0.5时高16.59%;模型1-4在分类阈值为0.2 时,Recall 比阈值为0.5 时高48.34%,RS_mean 比阈值为0.5时高13.44%。所以降低分类阈值后,5个模型都能提高对具有破产风险企业的预测准确率,并获得更好的预测性能。 表6 两种分类阈值的预测结果对比 根据所获得的最佳分类阈值,5 个模型对企业破产预测的最终分类结果如表7所示,图11是5 个模型的ROC曲线。 图11 基于改进随机森林的五种模型的ROC曲线 从表7可以看到,模型1-1 与模型1-0 相比,召回率Recall 提升了8.33%,特异度Specificity 降低了2.12%,召回率特异度均值RS_mean 提升了3.10%,精确率Preci‐sion 提升了0.31%,AUC 值提升了0.0031,说明经计算Pearson 相关系数并进行特征提取的模型比未进行特征提取的模型分类性能更佳。 表7 基于改进随机森林的五种模型的企业破产预测相关指标结果 模型1-2 与模型1-1 进行比较,召回率Recall 提升了6.67%,特异度Specificity降低了5.49%,召回率特异度均值RS_mean 提升了0.59%,精确率Precision 提升了0.20%,AUC 值提升了0.0056,说明对少数类采用SMOTE 过采样技术生成的新数据集能够显著提升TRF分类器分类结果的各项评价指标值,在处理企业破产预测问题上,SMOTE-TRF 模型的综合性能要比TRF 模型更优。 而结合综合采样的分类器与SMOTE-TRF 模型相比,模型1-3 即SMOTETomek-TRF 分类器在召回率上提升了2.5%,特异度Specificity 提升了0.24%,召回率特异度均值RS_mean 提升了1.37%,精确率Precision 提升了0.12%,AUC 值提升了0.0097;模型1-4 即SMOTEENNTRF 分类器在召回率上提升了12.5%,召回率特异度均值RS_mean 提升了1.17%,精确率Precision 提升了0.45%。 本文选取全球10173 个企业在2008年的财务比率以及在2013年的破产情况作为数据基础,通过结合特征提取、平衡化技术、改进的随机森林3种方法构建了企业破产预测模型。得出如下结论: (1)改进的随机森林模型相比于传统随机森林模型在召回率上提升了36.67%。 (2)本文提出的Pearson 相关系数特征提取规则能有效地从64 个财务比率中筛选出28 个来准确衡量企业各方面的能力,降低模型复杂度的同时,还提升了分类预测的各个评价指标值,对具有破产风险企业的预测正确率提升最为明显。 (3)3 种方法的结合能获得最高的预测性能,若平衡化技术选择综合采样的话,预测结果会比使用SMOTE方法更优。 (4)本文选取的研究对象是全球不同行业的公司,所以本文的研究方法在企业破产预测领域具有更高的普适性以及更加广阔的应用前景。 根据以上结论,提出以下建议:第一,金融政策方面要加强对企业破产预测模型的关注,加大对其研发资金的投入和研发人员的投入,使研究出来的模型具备实用性,而不仅仅只存在于理论方面,对于未来有可能会发生的经济危机的防范要有所准备,从而尽可能减小损失。第二,企业要加强自身管理,增强风险管理意识,可以根据自身的情况建立破产风险预警系统,不仅可以引入本文提出的相关财务指标,未来还可以根据外部环境和企业内部环境的变化,考虑与业务增长、公司管理和宏观经济学相关的变量,进而提高模型在预测公司破产时的准确性,将预测结果及时提供给企业的所有者和利益相关者(包括债权人、工会、政府机构、雇员、客户和供应商),从而使企业提前一步发现问题并采取战略行动,改善公司环境,达到减少损失甚至消除破产风险的目的。第三,要加强内部管控,保障所提供的财务数据真实准确,例如建立一套有效的管理信息系统,包括严密的授权及批准制度并要求全员执行,相关员工要定点盘点存货、加强会计系统控制等。第四,要提高公司主营业收入或者降低产品成本,提高盈利能力;合理有效地安排资本结构,加快资金周转率,提高营运能力,进而提高公司的盈利能力和偿债能力。

2 实验

2.1 实验数据与数据预处理


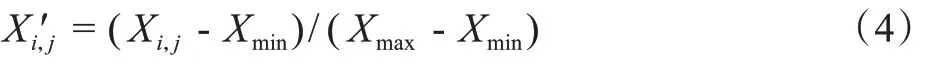
2.2 特征提取

2.3 类别平衡化


2.4 评价指标

2.5 改进随机森林模型建模






2.6 实验结果分析

3 结束语

