精准设计好问题，促进学生深思考

李进军

问题是数学的心脏，数学课堂教学应当从问题开始。提问是教师进行课堂教学最基本的手段，是教师课堂教学的主要策略。课堂上，师生通过提问进行信息交流和直接的双边活动。优秀的问题和精准的提问是优质的教与学的核心。下面笔者就如何精准提问，谈谈一些看法。

新一轮课程改革，要求我们的课堂教学不仅要关注学生学习的结果，更要关注学生学习的过程。在以问题促进思考的“疑-展-评”课堂上，我们常常把找结论的问题变为找理由的问题、找过程的问题、找方法的问题、找方案的问题，来引导学生展开思维过程。

一、把找结论的问题变为找理由的问题

“学起于思，思源于疑。”思维是从问题开始的，好的问题不仅能够引起学生的注意力，鼓励学生积极思考，营造活跃的课堂气氛，提高教学效果，而且也能够引导学生思考方向，扩大思维广度，提高思维层次。教学中，我们要根据教学目标、教学内容、教学过程、教学方法、教学评价及学生的认知水平等方面精心设计问题。下面，我们将探讨如何把找结论的问题变为找理由的问题，让学生更加关注 “为什么”，加深对知识的理解。

【片断1】“认识射线、直线”的教学

师：我们已经学过了线段，请同学们在练习本上画一条线段，并说一说它的特点。

生：线段有两个端点，可测量长度。

师：如果把你画的线段从一端一直画下去，会出现什么情况？

生：画到了纸的边上了，不能再画了。

生：如果纸足够大的话，我一直能画下去。

師追问：一直能画下去是什么意思？

生：就是无限长。

师：其实同学们刚才画的就是我们今天要学习的另外一种线叫射线（板书：射线），你能说说什么是射线吗？

……

上述教学从学生的已有知识经验出发，教师提出了一个“如果把你画的线段从一端一直画下去，会出现什么情况？”的思考性问题。在问题的引导下，学生在画的过程中展开想象，借助与直线和线段的比较来认识射线，理解了射线区别于直线及线段的特点。学生获得新知不仅限于结论，而且包括得出结论的理由。这个过程就是学生思维的过程，也是学生自主建构知识的过程，体现了新课程倡导的“评价既要关注学生学习的结果，也要重视学习的过程”的理念。

学生学习知识的过程，是一个自我建构的过程，他们在已有知识经验的基础上学习新知，然后再将学到的新知纳入到他们已有的知识系统中，形成知识体系。在以问题引导思维的课堂上，学生对“为什么”问题的回答，需要寻找支持自己答案的理由或依据，而寻找理由或依据的过程，需要对已有知识和经验进行回顾、选择和重构，这一过程就是思考的过程。学生在这样的过程中不断发展自己的思维。

二、设计找过程的问题

引导学生对自己的学习活动进行总结和反思，是帮助学生形成良好学习品质，提高学习能力和学习效益的重要措施，是教学的重要环节。在小学阶段，学生受年龄和认知水平的限制，对学习过程的关注往往不够，需要教师的引导。设计找过程的问题是引导学生关注过程，在过程中深化对知识的理解，掌握解决问题的方法。这样的问题能够引起学生对所学内容的回顾与整理，能够激发学生对所得结论的方法和过程进行探索，达到学会分析问题的目的。

【片断2】“平行四边形的面积”的教学

在导入新课后，教师直接提出：你们能把一个平行四边形变成一个长方形，来推导平行四边形的面积计算公式吗？

学生操作后汇报把一个平行四边形变成长方形的过程与方法。

师：观察拼出的长方形和原来的平行四边形，你发现了什么？

生：拼出的长方形的长与原来平行四边形的底相等，宽与原来平行四边形的高相等，长方形的面积与原来平行四边形的面积相等。

教师根据学生的回答板书：

长方形的面积=长×宽

平行四边形的面积=底 ×高

结论：平行四边形的面积=底×高

上述教学片断中，教师用问题“你们能把一个平行四边形变成一个长方形，来推导平行四边形的面积计算公式吗？”引导学生通过动手操作经历把平行四边形变成长方形的过程。在这个过程中，学生通过观察发现、比较思考后得出结论。这种先思考过程再得出结论的方法，不仅使学生经历了一个自主探究、自我发现的过程，而且对结论的认识与体会更加深刻。

三、设计找方法的问题

教学设计是根据教学对象和教学目标确定合适的教学起点与终点，将教学诸要素有序、优化地进行安排，形成教学方案的过程。它是以帮助学生的学习为目的，以学生学习所面临的问题为出发点，寻找问题，确定问题的性质，研究解决问题的办法，从而达到解决问题的目的。

找方法的问题就是在问题的引领下，让学生寻找解决问题的策略与方法，通过找方法，提高解决问题的能力。

【片断3】在教学“分数的大小比较”后，教师设计了如下问题：你能用哪些方法找出一个比大而比小的分数？

学生通过思考交流，有了以下方法：

方法1：通分法

<□<   ，<□<， 可填;

方法2：平均法

（+）÷2=;

方法3：倍数法

<□<      □=== ……

在学生找一个比大而比小的分数时，教师提出了“你能用哪些方法？”的问题。在问题引导下，学生不仅说出了答案也说出了方法，而且学生不自觉地在找到一种方法之后，思考其它方法，较好地培养了学生的发散性思维。

四、设计找方案的问题

培养学生解决问题的能力是新课程教学的重要目标。我们应该在教学活动中有计划、有目的地设计让学生找方案的问题，引导学生运用知识和经验去解决问题，调动他们主动学习、创新性运用知识解决问题的积极性。但学生的能力培养不是一蹴而就的，应该是阶段性的，不断上升和提高的过程。

找方案的问题一般需要运用发散性思维，在问题的引导下让学生提出各种不同的解决问题的方案。教学中，我们可以根据教学内容，多层次、多角度、多类型地设计问题，激发学生的思维，使学生的接收系统处于亢奋状态，形成全方位的交叉感知，有效地接收、加工和储存信息，从而培养学生的灵活性思维。

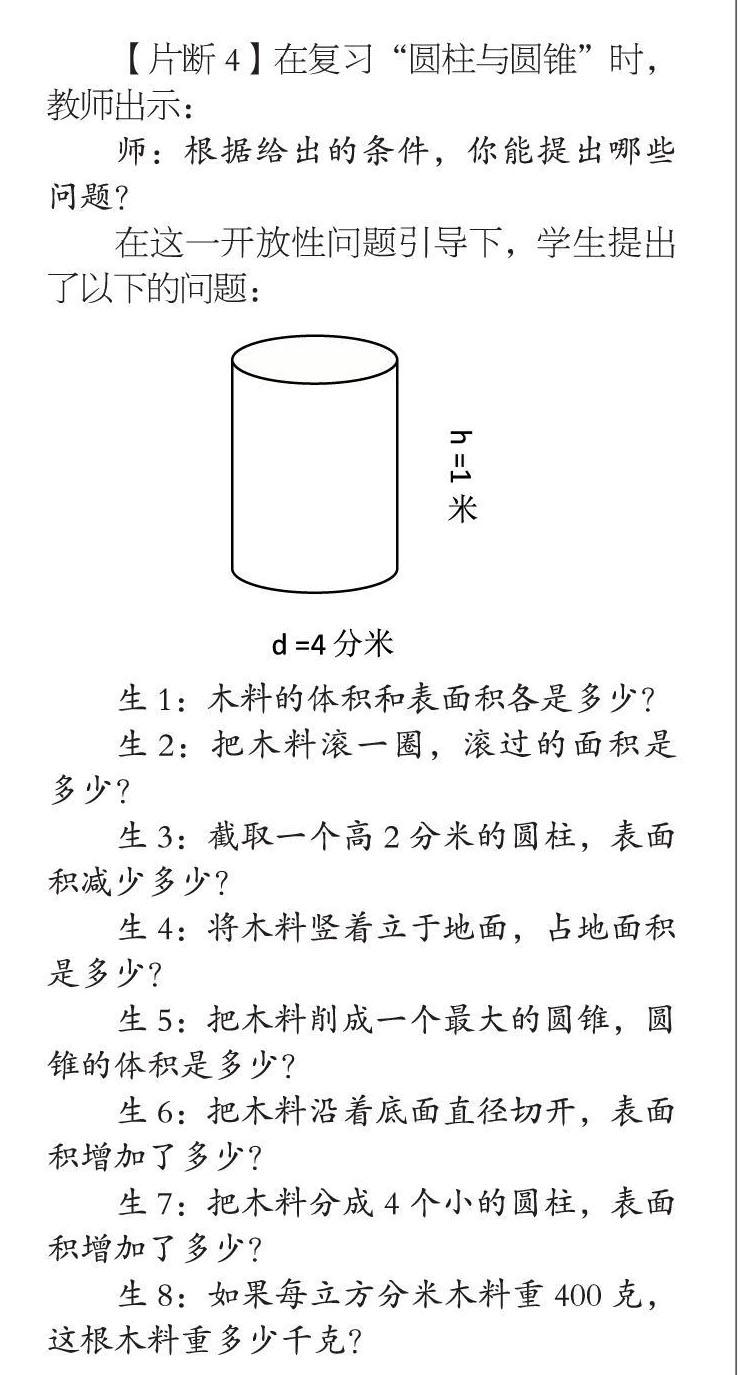
【片断4】在复习“圆柱与圆锥”时，教师出示：

师：根据给出的条件，你能提出哪些问题？

在这一开放性问题引导下，学生提出了以下的问题：

生1：木料的体积和表面积各是多少？

生2：把木料滚一圈，滚过的面积是多少？

生3：截取一个高2分米的圆柱，表面积减少多少？

生4：将木料竖着立于地面，占地面积是多少？

生5：把木料削成一个最大的圆锥，圆锥的体积是多少？

生6：把木料沿着底面直径切开，表面积增加了多少？

生7：把木料分成4个小的圆柱，表面积增加了多少？

生8：如果每立方分米木料重400克，这根木料重多少千克？

……

一般情况下，教师提出一个让学生计算木料的体积或表面积的封闭性问题，而这位教师在教学时所提的问题是：“根据给出的条件，你能提出哪些问题？”由于问题具有开放性，学生在回答中互相感染，提出了不同的问题，并进行正确解答。这一过程不仅极大地拓展了学生思维的空间，提高了学生提出问题、分析问题和解决问题的能力，而且也将复习引向深入，课堂气氛活跃，学生参与的积极性高。

开放性设计问题是考查学生思维能力和创造力的有效途径。课堂上，我们通过设计开放性问题，让学生设计不同的解决问题的方案，使学生有话可说，有法可想，从而激发学生的创新意识，培养学生的思维能力，将新课程的教学理念落到实处。

总之，在小学数学教学中，教师设计和提出能够引发学生思考的好问题，能够更好地推进我们的教与学。

责任编辑  杨  杰