基于深度神经网络的地震强反射剥离方法

田亚军, 高静怀* , 王大兴, 陈道雨

1 西安交通大学信息与通信工程学院， 西安 710049 2 海洋石油勘探国家工程实验室， 西安 710049 3 中国石油长庆油田公司勘探开发研究院， 西安 710018 4 低渗透油气田勘探开发国家工程实验室， 西安 710018

0 引言

在储层预测工作中常遇到强反射界面，这给储层的精确描述工作带来了极大困难.相邻地层波阻抗差异大是导致强反射界面出现的直接原因.一般煤系地层、深水稳定沉积形成的烃源岩层、风化层形成的不整合面等位置易形成强反射界面，而这类地层附近也容易产生油气聚集.强反射的存在，会淹没其附近储层的弱反射信号，导致储层预测工作无法正常进行.为此，开展强反射剥离研究对于储层弱反射信号的识别、结构的刻画、含油性检测并进一步辅助水平井设计提高钻探成功率具有重要意义(Guo and Wang, 2004；李海山等，2014；秦雪霏和李巍，2014；杜玉山等，2016；蔡文杰等，2019).

针对强反射附近的储层预测问题前人提出了诸多解决方案，主要包括三类思路：(1)去除或压制强反射，其中基于匹配追踪算法的研究最多，主要思想是根据强反射低频强能量的特性匹配出强反射分量然后将其去除(Wang, 2010；李海山等，2014；许璐等，2019；何峰等，2019).多子波分解方法通过不同主频的地震子波重构原始信号，从重构分量中去除反映强反射信号频段的分量达到去除强反射的目的(赵爽等，2007；佘刚等，2013；陈人杰等，2014).类似的，Wang等(2016a)使用EMD分解方法分解出强反射所在的固有模态分量并将其分离达到压制强反射的目的.(2)忽略强反射层的影响，通过调整时频分析方法的参数突出弱反射信号的时频特征(王宝江等，2012).(3)采用反Q滤波方法对强反射附近目标层反射波的相位和振幅进行补偿校正来增强弱反射信号的能量(Guo and Wang, 2004).本研究属于第(1)类.

在卷积模型的框架下可将强反射看成是强反射系数与地震子波卷积的结果(Robinson, 1985).构成强反射的关键要素包括强反射系数的位置、大小以及地震子波，若能够通过算法求解这三个要素，强反射就能被唯一的确定.然而，实际资料中的地震子波难以预测，加上强反射往往是由多个反射界面产生的反射波相互干涉叠加形成的复合波，导致原始地震记录与强反射之间存在非常复杂的非线性映射关系，传统方法难以求解这一映射关系.深度学习作为机器学习领域一个新的研究方向，不需要物理方程或理论知识就可以求解非常复杂的非线性映射问题(Kim and Nakata, 2018).更重要的是，当深度网络训练完成后可直接预测目标，不需要经验性调参.鉴于深度学习方法的强拟合性，大量的深度学习方法被应用于地震资料处理与解释，例如波阻抗反演(Das et al., 2019; Wu et al., 2020)、盐丘识别(Di and AlRegib, 2020; Shi et al., 2019)、初至拾取(Wu et al., 2019a；李薇薇等，2021)、层位解释(Lou et al., 2020; Wu et al., 2019b)、断层解释(段艳廷等，2019；Wu et al., 2019c; Liu et al., 2020)、储层预测(林年添等，2018；付超等，2018)、波形分类(赵明等，2019)、地震P波S波到时拾取(于子叶等，2018)以及地震成像(奚先和黄江清，2018，2020).

综上所述，本研究通过分析强反射产生的原因，在卷积模型的框架下建立含有强反射地震记录的生成模型；进一步将强反射预测问题分解成地震子波估计与强反射估计两个子优化问题，并引入交替迭代深度神经网络(AIDNN)和U-Net网络分别求解；根据求解优化模型的需求及训练样本的特点设计具体工作流程.最后通过模型数据及实际数据的试算，验证方法的有效性.

1 强反射层剥离问题分析及模型构建

地震记录可以看成地震子波与反射系数卷积的结果(Robinson, 1985)：

s(t)=w(t)*r(t),

(1)

其中s(t)是合成地震记录，*是卷积运算符，w(t)是地震子波，r(t)是反射系数.同样的，对于含有强反射的地震记录可以表示为：

s(t)=w(t)*rw(t)+w(t)*rs(t),

(2)

其中rw(t)是弱反射系数，rs(t)是强反射系数.图1简要阐明了带有强反射的地震记录的形成过程.显然，若能预测出强反射(ss(t)=w(t)*rs(t))并将其从地震记录s(t)中剥离，就能突出弱有效信号(sw(t)=w(t)*rw(t))能量.参照卷积模型框架下的反问题解法(Wang et al., 2016a)，本研究可以构建如下优化问题求解强反射：

(3)

式(3)中共有三个未知量：w(t)、rw(t)和rs(t)；这种含有三个未知量的反问题无法直接求解.

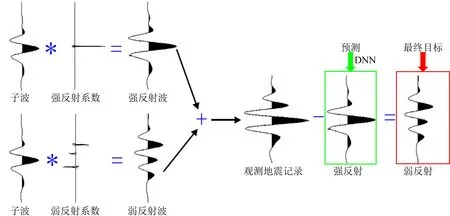
图1 强反射剥离原理Fig.1 Principle of strong reflection removal

强反射可以看成是强反射系数与地震子波卷积的结果；实际工作中，在一定空间范围内地震子波可以看成是时不变的；本文首先假设地震子波在待处理区域时不变，这样就能将式(3)中的地震子波分离出来单独求解.参照Chen 等(2019)的工作将地震子波预测问题分解为地震子波与反射系数交替求解的两个子问题，并采用AIDNN网络训练并求解.得到地震子波后，式(3)便剩下两个未知量rw(t)和rs(t).建立如下优化模型：

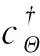
(4)

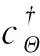
进一步假设在一定空间范围内反射系数序列同分布，选取同工区不包含强反射的地震数据作为弱反射地震记录sw(t)来训练式(4)中的优化问题.式(4)可以表示为：

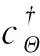
(5)

式(5)中仅包含一个未知量rs(t).

由于我们想得到的是强反射，为了方便训练地震记录与强反射的映射关系，将式(5)中的唯一未知量代换为ss(t)=w(t)*rs(t)；式(5)可表示为：

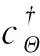
(6)

以相同工区相邻位置的数据作为训练样本带来的另一个好处是，样本sw(t)本身的噪声水平与分布规律可以看作与待处理地震记录s(t)一致.因此，在训练强反射ss(t)与地震记录s(t)之间的映射关系时不必考虑噪声.最后采用具有强大非线性映射能力的U-Net来求解这一问题.

2 基于AIDNN的地震子波预测

Adler和Öktem(2017)针对病态反问题提出了一种交替迭代深度神经网络(AIDNN)并将其应用于医学高分辨成像.AIDNN以传统最小二乘方法为先验约束解空间，进一步利用深度网络校正最小二乘解提高解的精度.Chen等(2019)将AIDNN应用于地震子波预测；本文借鉴Chen等人的工作建立地震子波预测方法.下面简要介绍该思想：

根据卷积模型(Robinson, 1985)，地震记录s(t)可以表示为：

s(t)=ω(t)*r(t)+n(t),

(7)

其中，*是卷积运算符，ω(t)是地震子波，r(t)是反射系数，n(t)是随机噪声.本研究的目标是求解w(t)，建立如下优化模型：

+Ψ(w(t)),

(8)

其中Φ(r(t))是r(t)的凸正则化函数，Ψ(w(t))是w(t)的凸正则化函数.受到Wang等(2016b)、Adler和Öktem(2017)的启发，将问题(8)分解为两个子问题，即：交替反演地震子波与反射系数.具体可分为如下两个步骤：

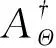
(9)

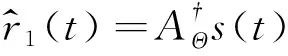
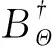
(10)

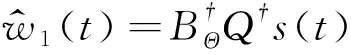
2.1 AIDNN网络结构

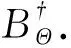
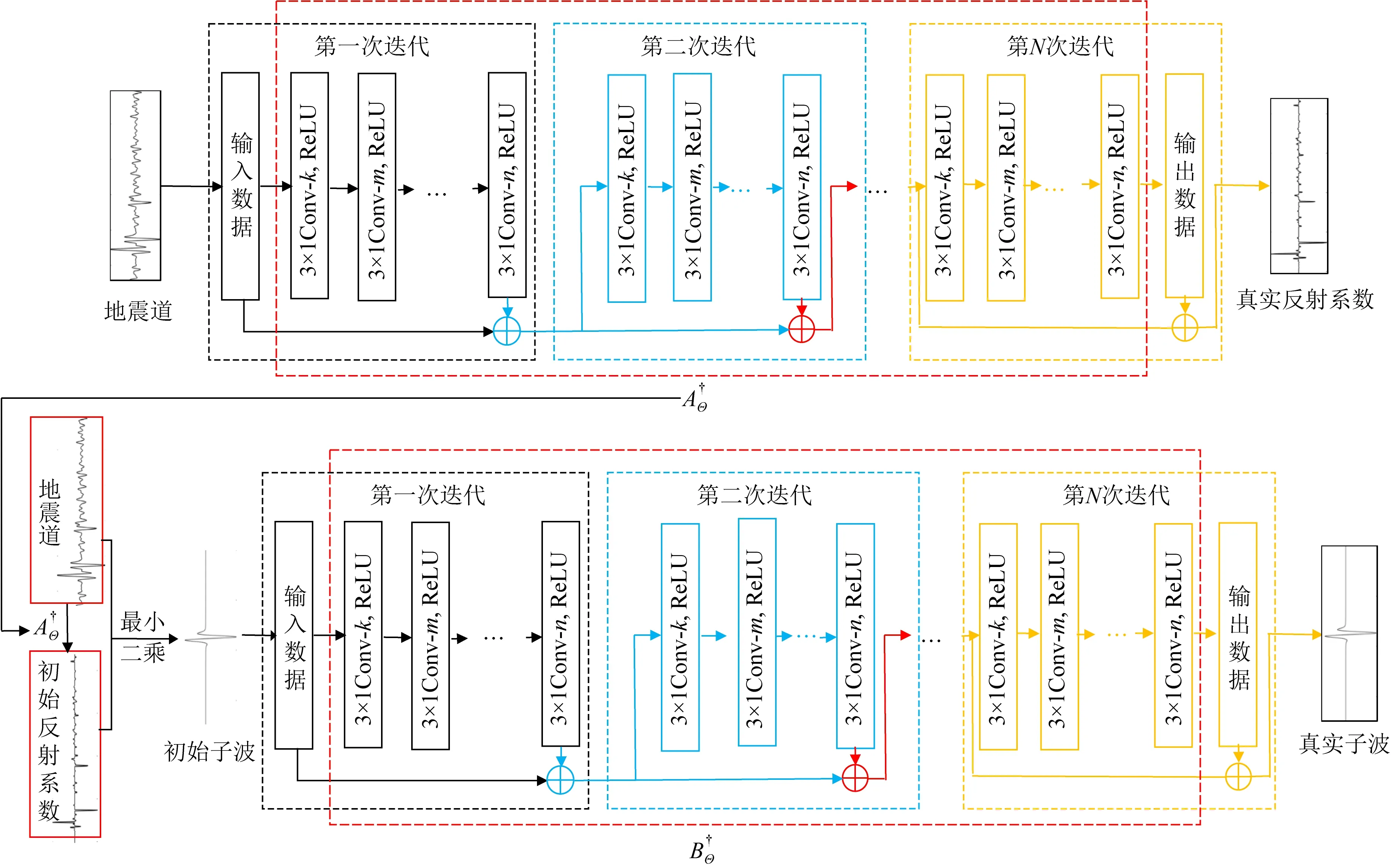
图2 训练地震数据与地震子波之间映射关系的AIDNN网络结构Fig.2 The structure of AIDNN network for training mapping relationship between seismic wavelets and seismic data

如图2所示，求解问题(9)与问题(10)所使用的网络结构相同.除第一次迭代与最后一次迭代包含输入输出层外，每次迭代使用的网络结构相同.每次迭代过程中隐层数量相同，本文使用三个隐层且每个隐层使用线性整流函数(ReLU)作为激活函数.卷积核大小为3×1.更多关于AIDNN网络理论基础可参见文献Adler和Öktem(2017).

2.2 训练样本

对于地震子波的预测问题，本研究选用的训练数据集包括地震子波、反射系数以及随机选择地震子波与反射系数并卷积生成的地震记录.其中反射系数序列来自于图3a所示的Marmousi模型，共包含737道数据，振幅范围归一化为[-1,1]，采样间隔为2 ms、时间采样点数为551.训练使用的地震子波为3801个不同相位与主频的雷克子波(相位范围为-90°～90°，采样间隔为1°；主频范围为20～40 Hz，

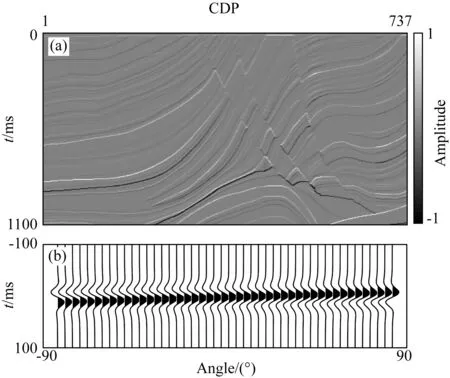
图3 用于地震子波估计的训练样本(a) Marmousi模型反射系数; (b) 雷克子波(主频20 Hz，相位-90°～90°).Fig.3 Training sample for estimating seismic wavelets(a) Reflection coefficient of Marmousi model； (b) Ricker wavelets (phases are from -90° to 90°, and dominant frequency is 20 Hz).

采样间隔为1 Hz；图3b所示为部分主频为20 Hz，相位介于-90°～90°之间的雷克子波样本).训练过程中随机抽取地震子波与反射系数并卷积生成地震道.

2.3 训练策略

3 基于U-Net的强反射层剥离

如式(6)所示，本研究将强反射预测问题构建成一个端到端的优化问题，并使用U-Net网络求解.U-Net网络首先由Ronneberger等(2015)提出并将其应用于医学图像分割.由于强大的非线性映射能力，U-Net被广泛应用于许多领域.对于地震数据处理和解释，其被应用到初至拾取(Hu et al., 2019)、断层识别(Wu et al., 2019c; Liu et al., 2020)等问题上，并取得了良好效果.

3.1 U-Net的网络结构

图4为U-Net的网络结构示意图，该网络的输入是带有强反射的地震记录道，输出为强反射.网络除输入与输出层外是一个U形的对称路径(即下采样路径和上采样路径).每个下采样步骤包含两个重复的卷积核大小为3×1的卷积层，每个卷积层后面是一个线性整流激活函数(ReLU)和一个2×1的最大池化层，每次下采样都将特征图大小减半.每个上采样步骤包括一个2×1的上采样卷积层和两个重复的卷积核大小为3×1卷积层，每个卷积层后面都有一个ReLU，每次上采样都将特征图大小翻一倍.更多关于U-Net的理论基础可参见Ronneberger等(2015).

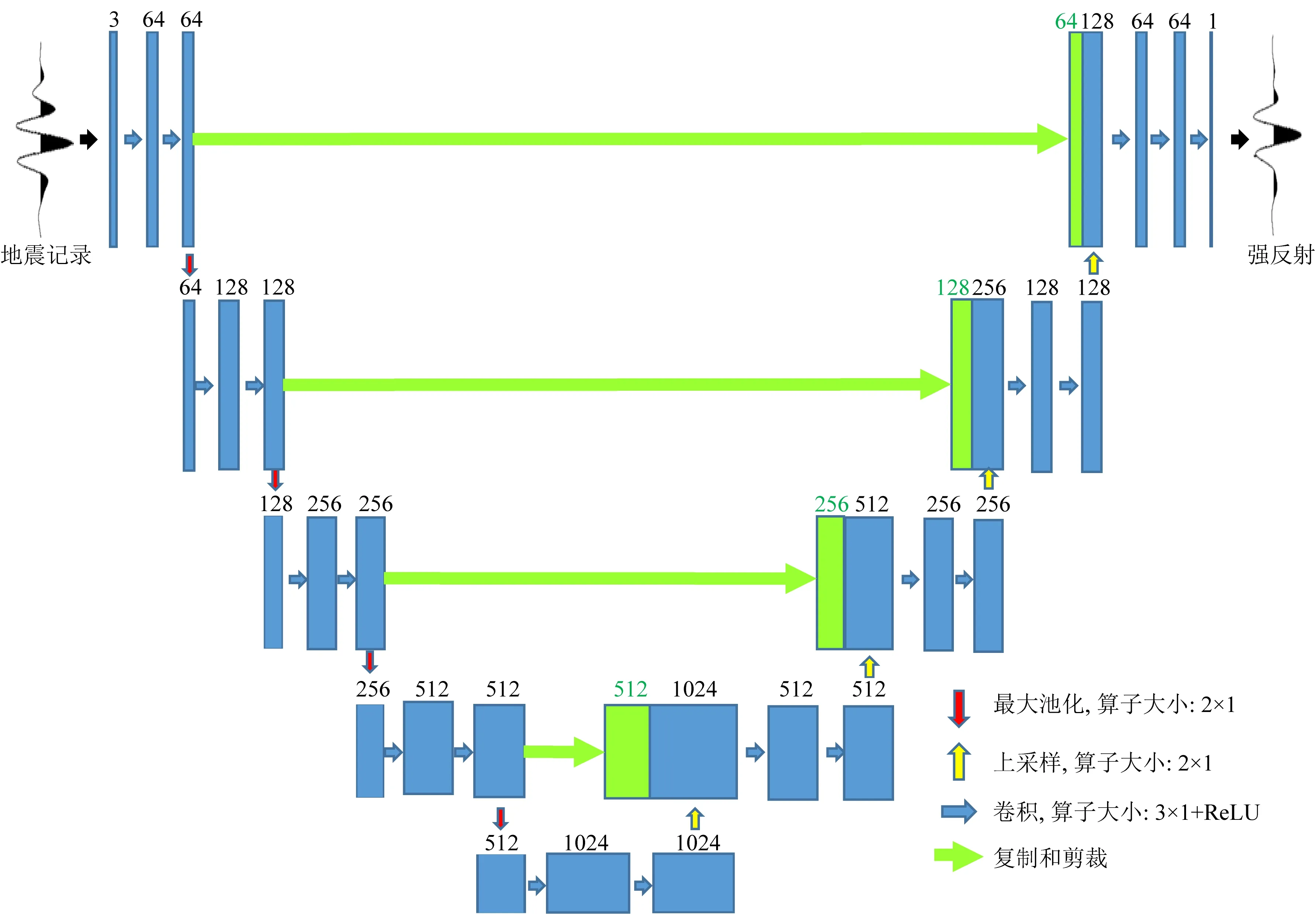
图4 用于地震强反射预测的U-Net网络架构Fig.4 Framework of U-Net network used in strong seismic reflection prediction

3.2 训练样本

在地震子波在一定空间范围内是时不变的且反射系数序列在一定空间范围内是同分布的假设下，本文建立了式(6)所示的强反射预测优化模型.预测强反射前，本文先确定强反射所在时窗范围，并选择强反射时窗附近的具有相同窗长的弱反射样本.在强反射系数的大小和位置均是随机的假设下，生成一系列振幅与位置均随机变化的强反射系数并与前文基于AIDNN网络求解的地震子波褶积获得强反射样本.随机抽取弱反射样本与强反射样本并将二者相加便得到了含有强反射的地震记录样本.至此便获得求解式(6)所需的所有训练样本.具体样本制作细节与方法实施步骤见第4节.

4 实施步骤

根据前文设计的强反射剥离优化模型，结合AIDNN与U-Net两个深度网络，本研究制定了图5所示的技术实施流程，具体内容如下：

(1)强反射层层位Hs拾取.

(2)确定强反射层层位Hs所在的时窗范围并将时窗范围分别向上或向下延伸一个波长获得待处理时窗范围Wts-te，窗口中的数据记为si，其中i代表道号.

(3)地震子波预测训练样本制作，包括三个内容：①选择典型地质模型的反射系数作为训练样本，本文参照Chen等(2019)的工作选择Marmousi模型作为反射系数训练样本；②确定地震子波主频大致范围，并设置主频与相位随机变化的雷克子波为子波的训练样本；③随机抽取反射系数与地震子波进行卷积获得地震记录样本；本文使用的具体训练样本参见2.2节.

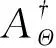
(6)待处理数据si预处理：强反射与弱反射最大的差异在于能量强，为了更好地使U-Net网络学习到这一知识，本研究对si的每一道分别做以强反射层Hs为中心的限幅处理使强反射层位置能量最强并对每道分别做归一化得到sig：

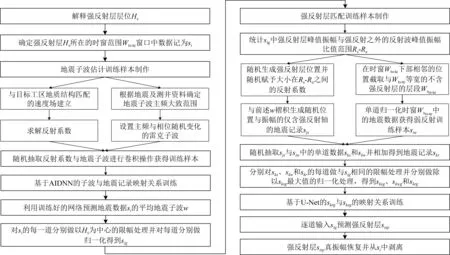
图5 强反射剥离工作流程图Fig.5 Work flow of strong reflection removal

sig(t)=si(t)⊙Giw(t)./max(si(t)⊙Giw(t)),

(11)

其中⊙为哈达玛积，代表对应元素相乘；max代表每道地震记录的最大值；Giw(t)代表限幅处理使用的高斯窗函数：

Giw(t)=e-a(t-ti0)2,

(12)

其中a控制高斯窗宽，ti0是每道地震记录强反射层所在时刻，i代表地震道道号.

(7)强反射训练样本制作：在卷积模型框架下，假设地震子波在一定空间范围内时不变，如果已知地震子波、强反射层反射系数的位置和大小，则强反射就唯一的确定下来了；据此，本文分三步构建强反射样本：①统计预处理后的数据sig(t)每道中强反射层峰值振幅与其次峰值振幅之比，确定所有道的比值范围Rs-Re；②在时窗Wts-te范围内生成位置随机且大小在Rs-Re范围内随机变化的强反射系数；③与步骤(5)中地震子波w(t)卷积生成强反射样本sjs，j代表第j次生成的强反射样本.

(8)弱反射训练样本制作：对于实际数据，在一定地质时期形成的地下地层之间存在必然联系并且地下地层的岩性和物性常呈周期性出现；据此，为了使样本训练更具针对性，本研究假设在一定空间范围内的弱反射界面的反射系数概率同分布；从待处理数据所在的时窗Wts-te下部相邻位置截取等宽的不含强反射的层段Wsts-te数据并做单道归一化作为弱反射样本siw.

(9)分别随机抽取sjs和siw中的单道数据sks和skw并将二者相加获得含强反射的地震记录skr，k代表第k次抽取的训练样本.

(10)训练样本预处理：分别对sks、skw和skr使用与步骤(6)相同的高斯窗函数进行限幅处理并分别对三者做除以sks最大值的归一化处理得到：

sksg(t)=sks(t)⊙Gkw(t)/max(sks(t)⊙Gkw(t)),

(13)

skwg(t)=skw(t)⊙Gkw(t)/max(sks(t)⊙Gkw(t)),

(14)

skrg(t)=skr(t)⊙Gkw(t)/max(sks(t)⊙Gkw(t)),

(15)

sksg、skwg和skrg分别是所需的强反射、弱反射和包含强反射的地震记录训练样本.

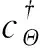
(13)使用式(16)逐道恢复强反射层真振幅：

sispr(t)=

(16)

其中/号代表对应元素相除.

(14)逐道从原始记录si(t)中减去强反射sispr(t)，获得强反射剥离后地震数据.

5 模型数据应用效果分析

为了验证本研究提出的强反射剥离方案的可行性和有效性，首先将其应用于理论模型数据的验算.

5.1 二维速度模型的建立与正演模拟

Chen等(2019)在论文中详细的对比了AIDNN网络应用于卷积模型制作的合成地震记录上预测地震子波的效果.为了使模拟结果更加接近真实情况，本研究使用能够更好的保证地震波传播过程中几何学与动力学特性的波动方程进行正演模拟.图6a为本研究使用的二维速度模型，红色箭头指示将产生强反射的反射界面，蓝色箭头指示需要识别的弱反射界面.子波采用图7中蓝线所示的主频30 Hz，相位-45°的雷克子波，采样间隔为2 ms；使用波动方程模拟炮集记录(Zhu and Harris, 2014; Zhang and Shi, 2019)并抽取零偏移距地震道作为待处理数据(图6b).不难看出，由于强反射层反射信号的存在，图6b所示的原始地震剖面下部目标层的反射信号淹没其中，无法识别(即图6b中无法识别图6a中蓝色箭头指示的反射界面反射的信号).

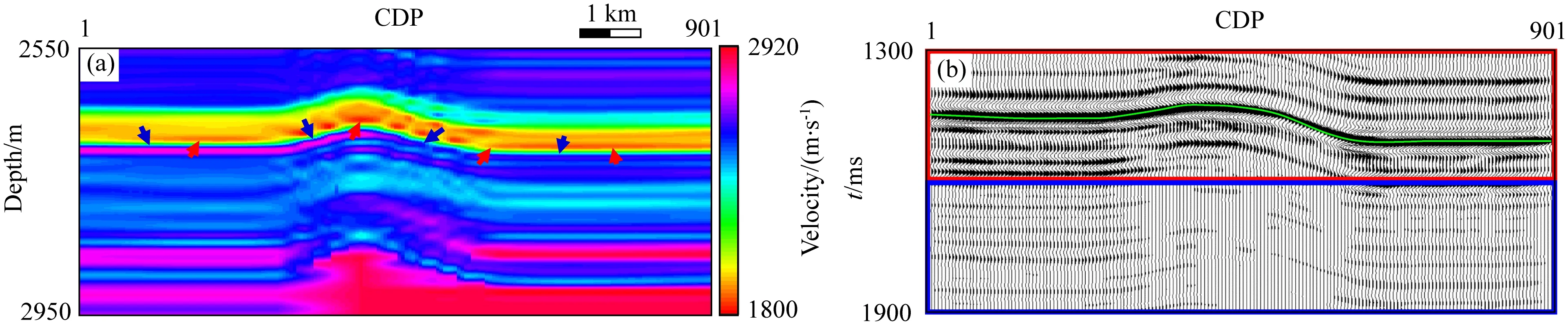
图6 二维地质模型及其模拟地震剖面(a) 二维地质模型，红色与蓝色箭头分别指示强反射界面和弱反射界面； (b) 模拟地震剖面，红框内为待处理部分，篮框内为弱反射训练样本，绿色曲线代表强反射层T0.Fig.6 Two-dimensional geological model and its simulated seismic profile(a) Two-dimensional geological model. The red and blue arrows indicate strong and weak reflection interface, respectively； (b) Simulated seismic profile. The red rectangle denotes the data to be processed. The blue rectangle denotes the training samples of weak reflection. The green curve indicates strong reflector T0.

5.2 应用效果分析

为了剥离强反射凸显目的层弱反射，本研究按照第4节中的实施步骤进行逐步处理.需要注意的是，图6b中红框内部为待处理数据，蓝框中为弱反射信号样本所在时窗.图7a所示为使用AIDNN网络预测的地震子波与实际子波对比，可见二者波形匹配较好；由图7b真实子波与预测子波之差可见，误差最大的位置是子波第二个旁瓣的位置为0.3，进一步说明了地震子波的预测效果；图8为模型数据强反射剥离前后结果对比分析，可以看到，相比于图8a所示的原始地震剖面，图8b所示的强反射剥离后的剖面中蓝色箭头指示的目标层弱反射信号凸显出来.图8c为预测出的强反射，其横向能量变化与波形变化与原始剖面(图8a)中的强反射一致，这说明了本方法良好的保真保幅性.

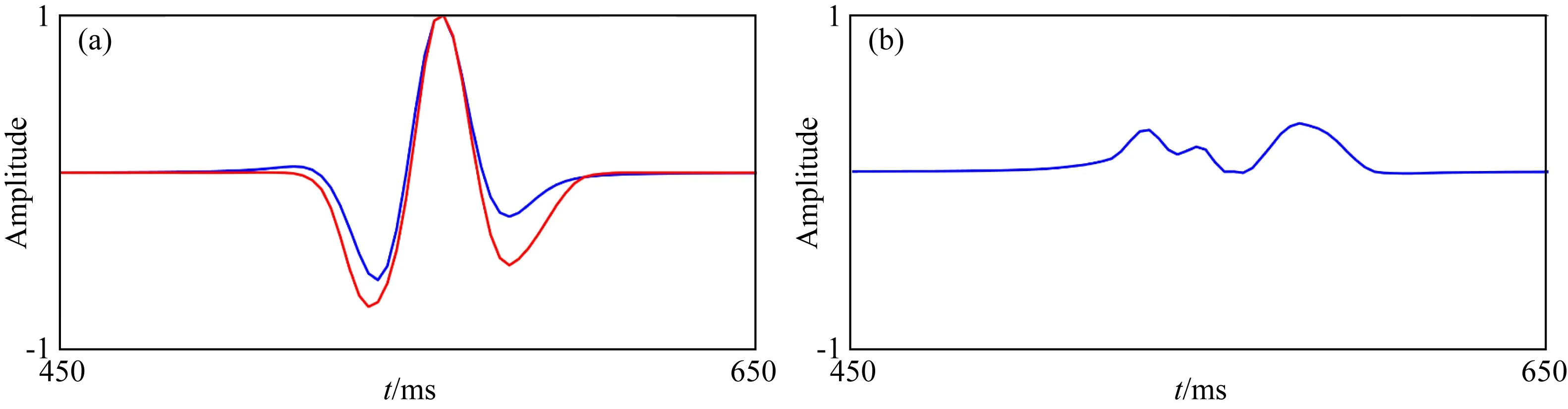
图7 实际地震子波与估计地震子波对比(a) 实际地震子波(蓝色曲线)与估计地震子波(红色曲线)； (b) 预测结果与真实结果之差.Fig.7 Comparison of real and estimated seismic wavelets(a) Real (blue curve) and estimated (red curve) seismic wavelets； (b) Difference between estimated and real seismic wavelets.

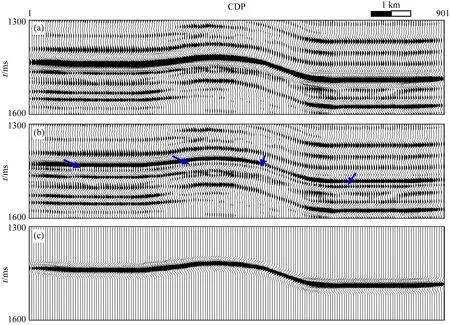
图8 模型数据的强反射剥离(a) 原始地震剖面； (b) 强反射层剥离后的地震剖面，蓝色箭头指示弱反射信号； (c) 强反射.Fig.8 Strong reflection removal of synthetic data(a) Original seismic profile； (b) Seismic profile after strong reflections removed. Blue arrow indicates weak reflection signal； (c) Strong reflection.

6 实际数据应用效果分析

本节选择储层在强反射下方的典型叠后地震剖面作为研究对象，通过本研究提出的强反射剥离方法辅助储层砂体结构表征.

6.1 实际数据及其地质背景

待处理数据选自中国西北鄂尔多斯盆地古峰庄地区，目的层是河流沉积体系演化为大型三角洲沉积体系过程中形成的优质储层；其上部层段为厚达40 m的低速烃源岩，形成于深水湖盆时期；这为下部储层提供了良好的生油与封盖条件，二者形成了最佳的成藏组合关系.但由于烃源岩与围岩波阻抗差大导致了强反射同向轴T0的形成，加之烃源岩与储层相邻导致下部储层反射信号被淹没在强反射之中，难以有效识别，这严重影响了储层预测工作(屈雪峰等，2017).因此，本节针对该工区实际叠后地震资料展开强反射剥离工作，以辅助储层砂体展布形态的刻画.

6.2 应用效果分析

图9为待处理的二维过井叠后地震剖面，共901道，道间距20 m，采样间隔2 ms.其中红框内为待处理数据，绿线代表待剥离强反射层T0，T0下部为河道砂体储层，探测这部分信号是该工区重要任务.图9中蓝框内的数据为弱反射层训练样本所在时间窗；另外，为了增加样本数量，我们截取临近30条CMP线上的相同时窗内的共27030个地震道作为弱反射样本.按照第4节中实施步骤进行逐步处理.图10所示为地震子波预测结果.

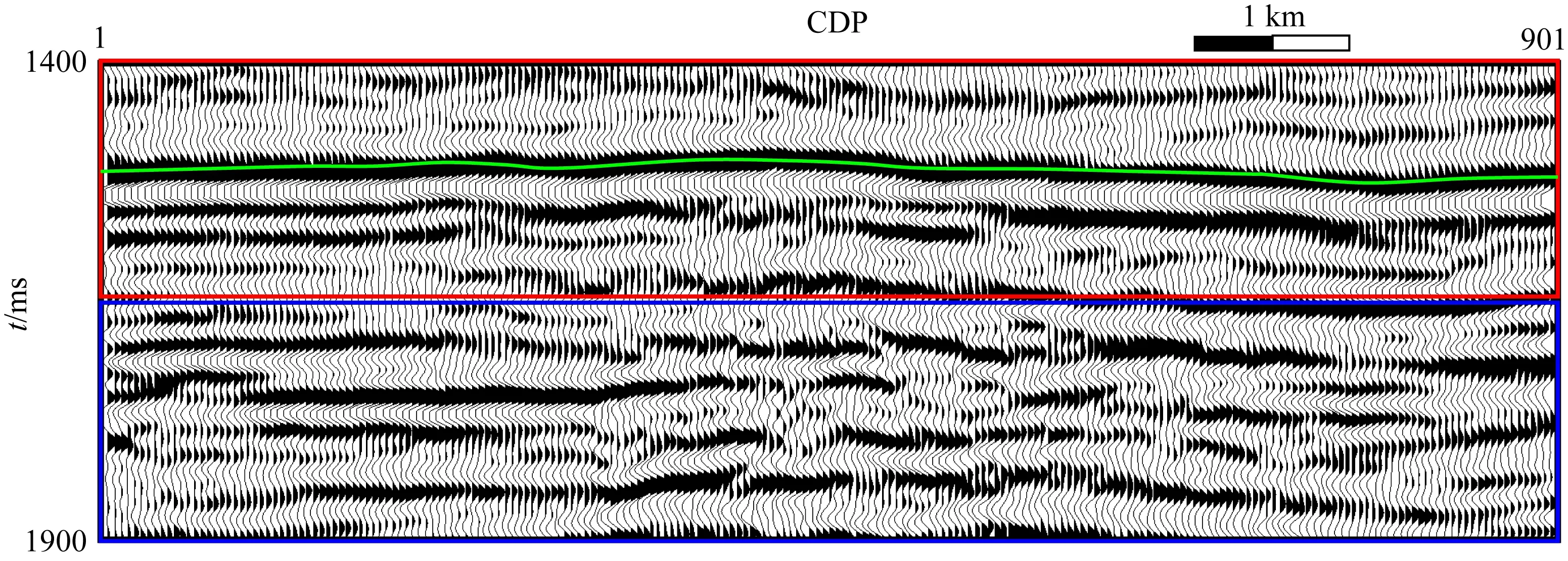
图9 待处理的原始地震剖面红框内为待处理数据；蓝框内为弱反射训练样本；绿色曲线指示强反射层T0.Fig.9 Original seismic profile to be processedThe red rectangle denotes the data to be processed. The blue rectangle denotes the training samples of weak reflection. The green curve indicates strong reflector T0.

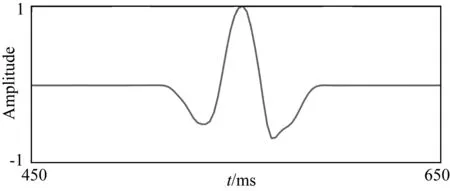
图10 基于AIDNN估计的实际地震子波Fig.10 Seismic wavelet of real seismic data estimated by AIDNN

图11为实际资料强反射剥离效果对比分析.从图11a所示的原始剖面中的自然伽马曲线(红色曲线)与声波速度曲线(蓝色曲线)不难看出，强反射下还有一个层位(蓝色箭头指示)；但在地震剖面上该层位反射波淹没在其上部强反射之中无法识别.图11b是使用本文方法剥离强反射后的地震剖面，可见强反射下部蓝色箭头指示的弱反射轴显现出来且其位置与井曲线上指示的位置一致.图11c为剥离出来的强反射，与图11a中强反射层对比可见，二者横向上的能量与波形的变化一致且图11c中强反射之外无任何能量，这进一步说明了本文方法的有效性.

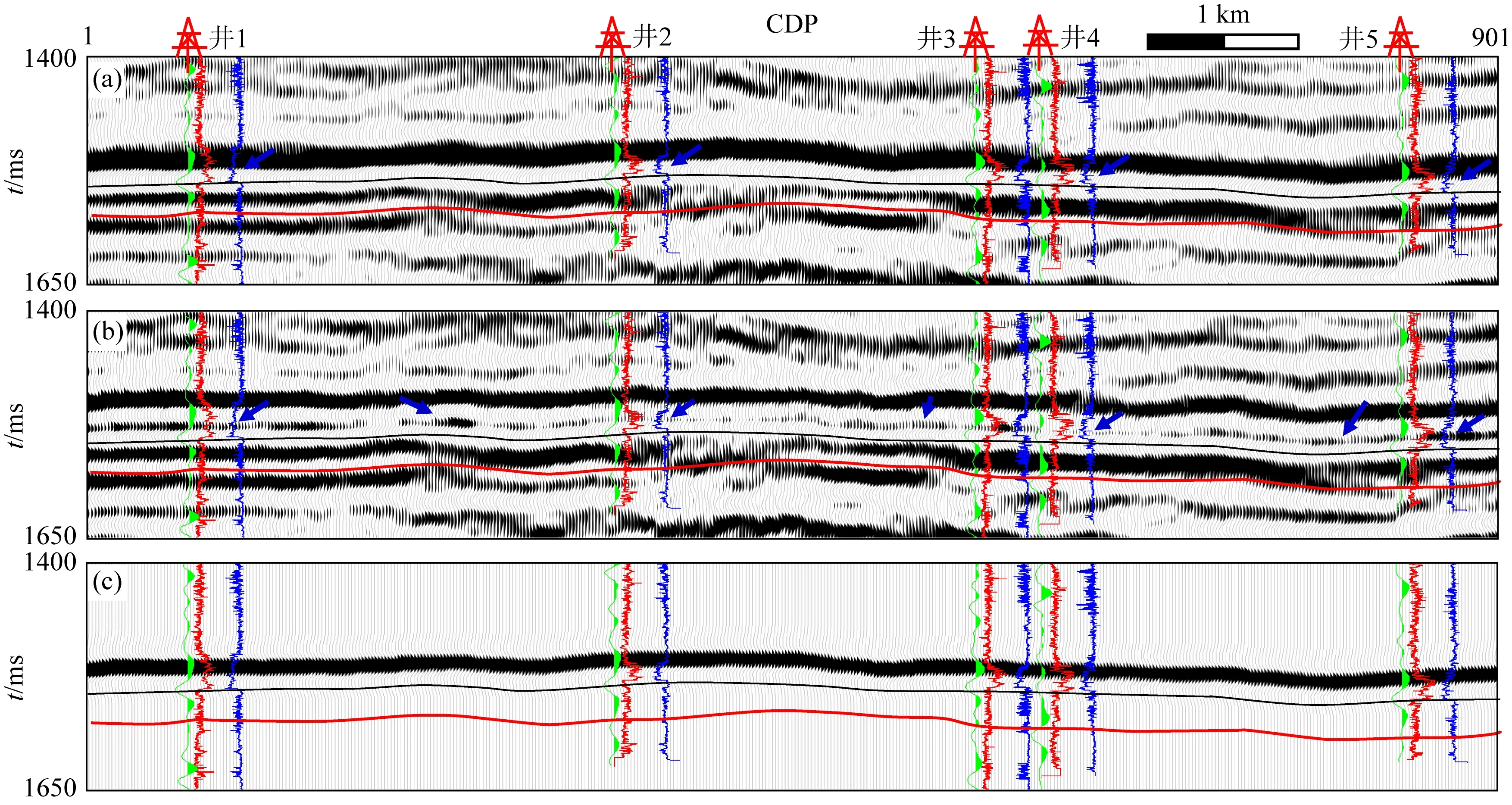
图11 实际地震数据强反射剥离(a) 原始地震剖面，蓝色箭头指示井曲线上的弱反射层； (b) 强反射层剥离后的地震剖面，蓝色箭头指示弱反射信号； (c) 强反射；另外，(a)—(c)中绿色地震道为合成记录，红色曲线和蓝色曲线分别是自然伽马曲线与声波速度曲线；水平方向的黑色曲线和红色曲线之间是待预测储层砂体所在区间.Fig.11 Strong reflection removal of real data(a) Original seismic profile. The blue arrow indicates the weak reflector on the well curve； (b) Seismic profile with strong reflections removed. Blue arrow indicates weak reflection signal； (c) Strong reflection. In (a) — (c), green seismic traces are synthetic seismic records, red and blue curves are gamma ray curves and acoustic velocity curves, respectively. Between black and red curves in horizontal direction is the sand body to be predicted.

为了进一步说明效果，将实际剖面中井2与井4的测井曲线与井旁道抽取出来进行对比分析(如图12所示).图12中黄线位置是强反射层位置，从测井曲线上可以看到其下部蓝色箭头指示的目标层位，强反射轴剥离之前在井旁道上无法显示这一层位产生的反射信号，将强反射剥离后该层位弱反射能量凸显出来且位置与井点上显示的位置一致(蓝色箭头所指).

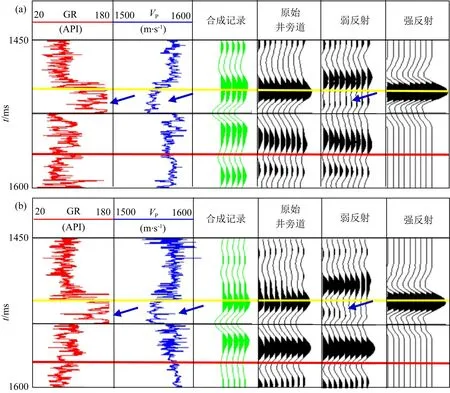
图12 在井旁道分析强反射剥离结果(a) 井2； (b) 井4.Fig.12 Analysis of strong reflection removal results in borehole-side trace(a) Well 2； (b) Well 4.

进一步分别对图11中强反射剥离前后的地震剖面用优化三参数小波变换(Tian et al., 2020; 高静怀等，2006；Liu et al., 2017; 高静怀等，2018)分解为图13与图14所示的20 Hz、30 Hz、40 Hz和50 Hz的谱分量来分析储层砂体展布情况(Lu and Li, 2013; Liu et al., 2019).图13为强反射层剥离前谱分解结果，不难看出，低频部分(图13a、b)目的层无法和强反射分离，高频部分(图13c、d)受强反射影响目的层内部能量弱，无法准确分析砂体分布情况.图14为强反射剥离后的谱分解结果，可见在目的层范围内不同频率成分谱分解结果均不受强反射的影响.从图14d高频50 Hz谱分解结果来看，由浅至深存在三个砂体结构且谱分解结果能够清晰的描述三个砂体展布情况(蓝箭头、红箭头和黑箭头分别指示第一至第三个砂体分布情况).此外，观察五口井的自然伽马曲线，不难看出，自然伽马曲线低值位置箭头指示的砂体位置与50 Hz谱分解结果一致；相对而言图13d所示的含强反射的原始剖面的谱分解结果无法清晰刻画着三个砂体，尤其是与强反射较近的第一个砂体的展布情况；这进一步说明本研究构建的强反射剥离方法的效果及其对这类储层预测的重要性.

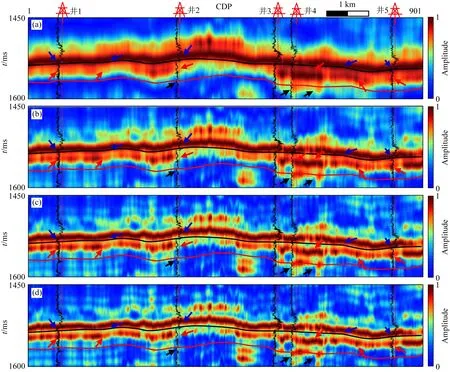
图13 强反射剥离前谱分解结果(a)—(d)分别是由三参数小波变换计算的20 Hz、30 Hz、40 Hz、50 Hz频谱分量.井点位置黑色曲线代表自然伽马曲线.Fig.13 Spectral decomposition results before strong reflection removal(a)—(d)are 20 Hz, 30 Hz, 40 Hz and 50 Hz spectral components calculated by the three-parameter wavelet transform, respectively. The black curves on the well points are the gamma measurements.

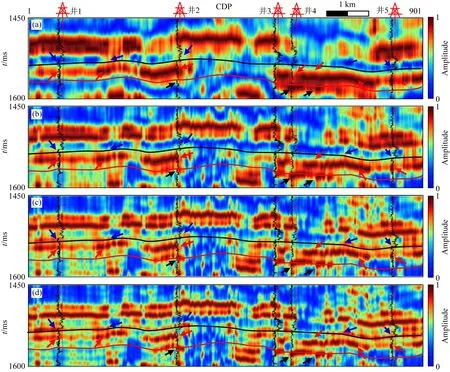
图14 强反射剥离后剖面谱分解结果(a)—(d)分别是由三参数小波变换计算的20 Hz、30 Hz、40 Hz、50 Hz频谱分量.井点位置黑色曲线代表自然伽马曲线.Fig.14 Spectral decomposition results after strong reflection removal(a)—(d)are 20 Hz, 30 Hz, 40 Hz, and 50 Hz spectral components calculated by three-parameter wavelet transform, respectively. The black curve on the well point are the gamma measurements.

进一步对上述工区55 km2的三维叠后地震数据体目的层强反射进行强反射剥离处理验证本文方法对三维实际数据的适用性和实用性.待处理数据Inline范围为150～400间隔为1，Crossline范围为60～600间隔为1，共135791道地震数据，每道351个采样点，采样间隔2 ms，数据大小212 M.本研究在TensorFlow框架下编写Python语言程序，在一块i7-8700 CPU上进行计算，训练地震记录与地震子波之间映射关系需要3 h 31 min，训练地震记录与强反射之间的映射关系需要44 min；对目标区域的预测及剥离过程使用了30 min.这里地震记录与地震子波之间映射关系的训练结果可以推广应用至其他工区；地震记录与强反射之间的映射关系训练结果仅能应用于目标工区，这与选择的弱反射训练样本有关.图15分别为强反射剥离前后对20 Hz与50 Hz谱分解结果做的沿层切片，其中20 Hz单频切片表征厚砂体平面展布范围，50 Hz单频切片表征薄砂体平面展布范围.不难看出，强反射剥离前20 Hz(图15a)与50 Hz(图15b)的单频切片结果差异小，刻画的信息大部分为强反射的频率成分，无法精细刻画目的层不同厚度砂体平面展布范围.利用本文提出的强反射剥离方法处理后地震数据计算的20 Hz(图15c)与50 Hz(图15d)单频切片高低频特征差异明显，能够精细刻厚砂体与薄砂体平面展布特征.

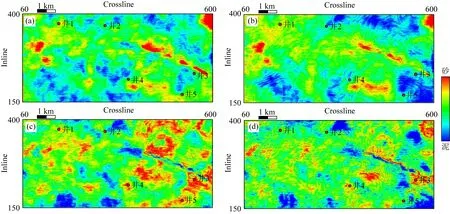
图15 强反射剥离前后砂体平面展布预测效果对比(a)和(b)分别为强反射剥离前20 Hz、50 Hz沿层切片； (c)和(d)分别为强反射剥离后20 Hz、50 Hz沿层切片.Fig.15 Comparison of prediction results of sand-body distribution before and after strong reflection removal(a) and (b) are 20 Hz and 50 Hz horizon slices before strong reflection removing, respectively；(c) and (d) are 20 Hz and 50 Hz horizon slices after strong reflection removing, respectively.

7 结论与讨论

本文提出了一种基于深度学习网络的地震强反射剥离方法，并用于辅助被强反射压制的储层弱反射信号的检测工作.利用深度学习网络我们可以全自动地实现端到端的复杂非线性映射，在提升处理效果的基础上省去专业处理和解释人员大量的经验性调参过程，计算速度快，适用于大规模三维地震数据处理，可以大大提高该类储层的解释精度与工作效率.得到如下结论：

在卷积模型的框架下构造的包括地震子波、强反射系数和弱反射系数三个未知量的强反射预测反问题的多解性非常强，即便是能够求解复杂非线性映射问题的深度学习方法也难以直接求解.本文假设地震子波在一定空间范围内时不变，设计先求解地震子波后估计强反射的工作流程，将强反射预测问题分解为地震子波预测与强反射预测两个端到端的子优化问题，并分别采用AIDNN与U-Net两个深度网络进行求解.模型资料试算结果表明，本文提出的方法在不伤害强反射周围有效反射信号的前提下能够准确剥离强反射，且保真保幅性好.实际资料的强反射剥离结果及在该结果基础上进行的储层砂体展布预测结果在井点处与测井解释结果一致.以上效果得益于：(1)假设地震子波在一定空间范围内时不变，将难以求解的强反射预测问题分解为子波预测与强反射预测两个端到端的优化子问题；(2)假设强反射附近的不含强反射的资料与强反射预测时窗内的弱反射近似同分布，选择强反射附近的资料作为弱反射训练样本，保证了训练样本的代表性且避免了训练过程中噪声的影响；(3)通过对训练样本与待处理数据的预处理，放大强反射特征，使得深度网络更容易学到强反射的特征.综上所述，本文提出的方法能够有效的应用于强反射剥离，这为该类储层的预测工作提供了重要技术支撑.

本研究虽然取得了重要进展，但仍然存在以下两点问题需要进一步探讨：(1)训练样本：训练样本设置的合理性对于深度网络的训练效果影响很大，理想数据集的每一类别都需要充分的样本数量，并且能够覆盖地震波形所具有的各种复杂特征；本文在模型数据应用部分预测的地震子波并不理想，导致这一结果的原因有以下几点：①在卷积模型框架下制作的合成地震记录训练样本不能很好的模拟地震波传播过程中几何学与动力学特性；但本文为了增加难度，验证算法所使用的模型数据是采用波动方程正演得到的.②地震子波训练样本只选用了雷克子波，但实际资料中子波的基本形态，它的频宽，仅用瑞克子波并不能很好地描述.③训练地震数据与地震子波的映射关系时没有加入待研究工区的实际地下地质规律，仅选用了Marmousi模型的反射系数.针对训练样本的三点问题，拟提出以下三点探索计划：①考虑地震波传播过程中几何学与动力学特性，在波动方程框架下模拟得到地震记录训练样本.②进一步扩大地震子波样本库，在雷克子波的基础上进一步加入俞氏子波、带通子波、统计子波等作为地震子波训练样本.③结合测井数据设计更加匹配待处理工区的地质模型，并获得反射系数训练样本.(2)泛化性：本研究假设在一定空间范围内地震子波时不变，且反射系数同分布；超出一定范围便不满足这些假设；因此，处理不同工区资料时都需要花费时间重新训练实际地震道与强反射之间的映射关系；为了使训练结果泛化性能更好，应当进一步总结不同地震资料反射层分布特征，设计更具代表性的样本，以增加训练样本的复杂性及普适性，从而使得所提出算法的训练结果普适性更好.

致谢感谢审稿专家对本文提出的宝贵意见和建议，感谢中国石油长庆油田公司勘探开发研究院提供的实际地震数据.