新型盘式横向磁通永磁无刷电机的结构原理及设计优化

张文晶 徐衍亮 李树才

（1.山东大学电气工程学院 济南 250061 2.山东精创磁电产业技术研究院有限公司 临沂 276000）

0 引言

随着工业机器人应用场合的不断增加，工业机器人的各种相关技术进入高速迭代升级阶段[1-2]。工业机器人主要由本体、伺服系统、减速器、控制器四部分组成，伺服系统作为其关键执行环节，又包括伺服驱动器和伺服电机[3]。目前主流工业机器人伺服系统大多采用永磁同步交流伺服电机（Permanent Magnet Synchronous Motor, PMSM）（以下简称伺服PMSM），相较于以往的直流伺服电机或步进电机，伺服 PMSM 精度高、效率高、功能全[4-5]。主流厂商生产的工业机器人搭配的伺服 PMSM 主要是传统的表贴式永磁同步电机（Surface Permanent Magnet Synchronous Motor, SPMSM），这种电机具有结构简单、运行可靠的优点[6]，但是由于其具有轴向绕组端部，电机轴向长度增加；工业机器人在停电状态下，要求机器臂断电停摆，伺服电机需要配套相应刹车系统，即制动器，同时作为伺服电机，还应配置编码器等反馈装置，这些装置均被安装在电机轴向前后两侧，进一步增加了电机轴向长度；另外传统SPMSM的转子体积和质量较大，增加了电机的转动惯量，转子转动惯量对电机起动和制动性能有着直接影响，在工业机器人要求频繁起停的应用场合下[7]，该问题就会尤为显著。

横向磁通电机（Transverse Flux Motor, TFM）由于其电路和磁路相互解耦，电机空间设计更为灵活，同时也具有更高的转矩密度，相较于传统永磁电机更利于实现小型化。文献[8]提出一种应用在小型电动汽车直驱系统中的新型爪极横向磁通电机，电机采用外转子结构，转子部分使用环形永磁体，具有更高的转矩密度。文献[9]提出一种双相交链的横向磁通永磁同步电机，这种电机具有更高的空间利用率，永磁体利用率也得到提高，有效增加了电机空载反向电动势。文献[10]提出一种H型铁心横向磁通磁阻电机，由于相邻两相间磁路耦合状况有效改善，电机的功率密度显著提升。然而目前针对工业机器人应用的横向磁通电机还未见相关研究。

文献[11]提出了一种 C型铁心结构盘式横向磁通电机，该电机集合了盘式轴向磁通电机以及横向磁通电机的特点，具有结构紧凑、转矩密度高以及转动惯量低的优势。使用该结构电机应用到工业机器人伺服电机中，不仅可以实现电机小型化，同时电机动态性能也可进一步提升，但是该电机相邻定子铁心间槽口面积大，导致有效气隙和齿槽转矩增大，漏磁现象也更为严重[12]。针对文献[11]所提出电机结构存在的问题，结合软磁复合（Soft Magnetic Composite, SMC）材料高频铁耗低、各向同性、易于成形等明显优势[14]，文献[13]提出采用SMC材料制作定子铁心极靴，从而减小槽口面积，使电机性能得到进一步提升。然而上述文献采用的C型铁心结构盘式横向磁通电机仍存在外径尺寸大、装配及拆卸工艺复杂等问题。将文献[13]中电机的C型定子铁心拆分为两块U型定子铁心分别固定在转子盘前后两侧，即得到本文提出的新型盘式横向磁通永磁无刷电机（Disk Transverse Flux Permanent Magnet Brushless Motor, DTFM），电机整体结构如图1a所示，采用该结构，电机装配难度有效降低，同时外径尺寸减小，尽管电机轴向长度会有一定程度增加，但是可以通过预留合理的定子内周空间用于安装工业机器人伺服电机制动器等配件，从而有效缩短电机轴向长度。

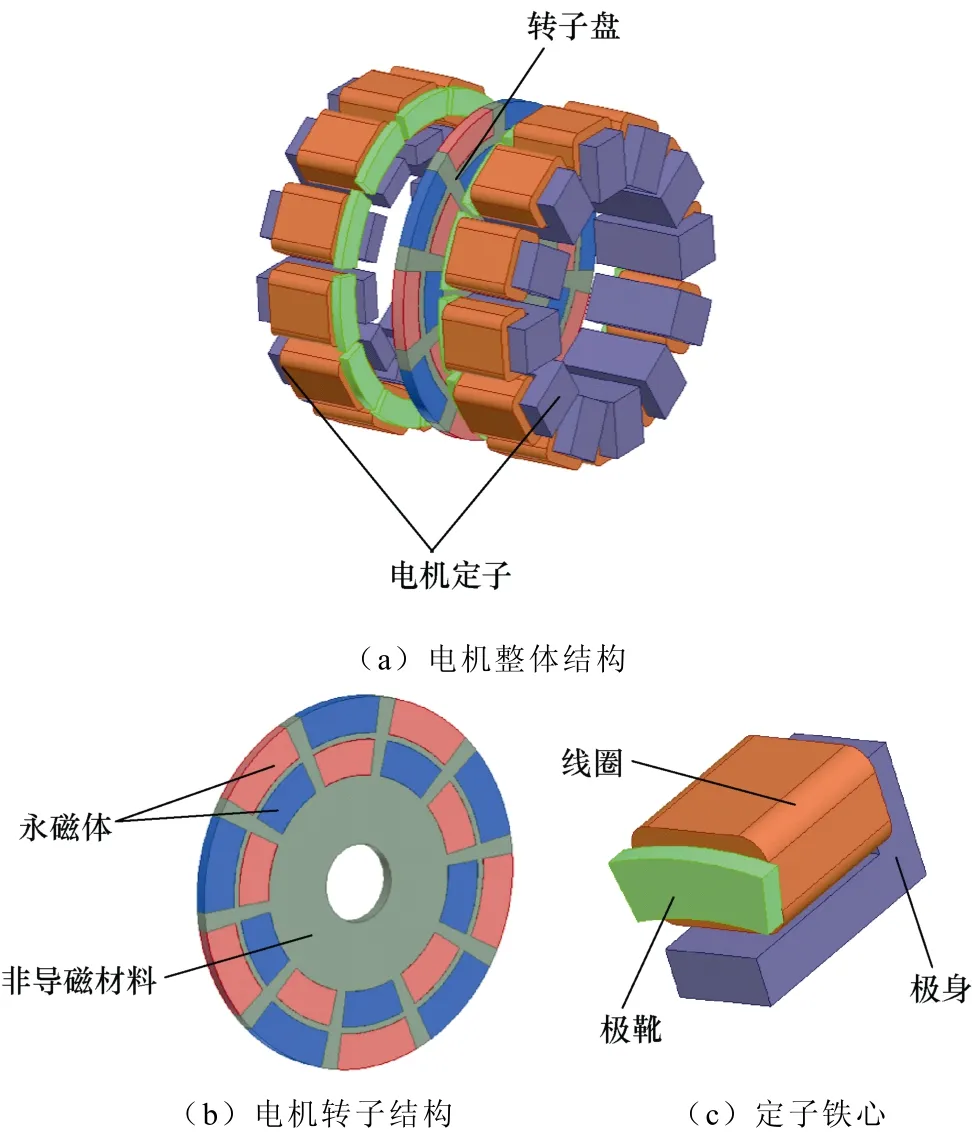
图1 电机结构Fig.1 Structure of DTFM

本文首先介绍了DTFM的结构及工作原理，然后对电机的功率方程进行推导，以此来确定电机的主要尺寸。经过初始设计后，电机虽然能够满足基本设计指标，但是其齿槽转矩等参数往往还需要进一步优化，本文选取定子极靴及转子永磁体的结构参数进行分析，研究其对电机性能参数的影响，然后采用一种新型多目标优化策略对电机进行优化，优化后的结果使用三维有限元方法（Three Dimensional-Finite Element Method, 3D-FEM）进行验证并与初始设计方案进行比较。最后设计制作一台实验样机，通过空载及负载实验对电机工作原理及性能进行验证。

1 DTFM的结构及工作原理

本文提出的DTFM的转子部分由永磁体和非导磁材料制成的圆盘组成，如图1b所示，在转子盘上有两组沿圆周方向分布的永磁体，沿径向方向，分别称为内永磁体组和外永磁体组，每组均包含 10块N极、S极交错排列的永磁体，径向上下两块永磁体极性相反。

电机定子部分由分布在转子盘前后两侧的两个定子盘组成，每个定子盘由沿圆周方向均匀分布的12块定子铁心构成，图1c为一块定子铁心的结构示意图，其包含一块硅钢片叠压制成的C型铁心极身、一块 SMC材料制成的扇形铁心极靴和缠绕在一个C型铁心臂上的线圈。

图1给出的 DTFM为三相 10极12槽结构，DTFM定子部分采用无轭分块电枢结构，沿轴向前后一对定子铁心和它们所夹的径向上下一对永磁体共同组成电机主磁路，如图2所示。沿圆周方向以及径向相邻两个永磁体极性相反。当转子旋转时，定子铁心内磁通交变，缠绕在定子铁心上的电枢线圈内感生出感应电动势。当定子绕组通三相交流电时，形成同步速旋转磁场，与永磁体产生的磁场相互作用，产生同步电磁转矩，进而驱动电机旋转。

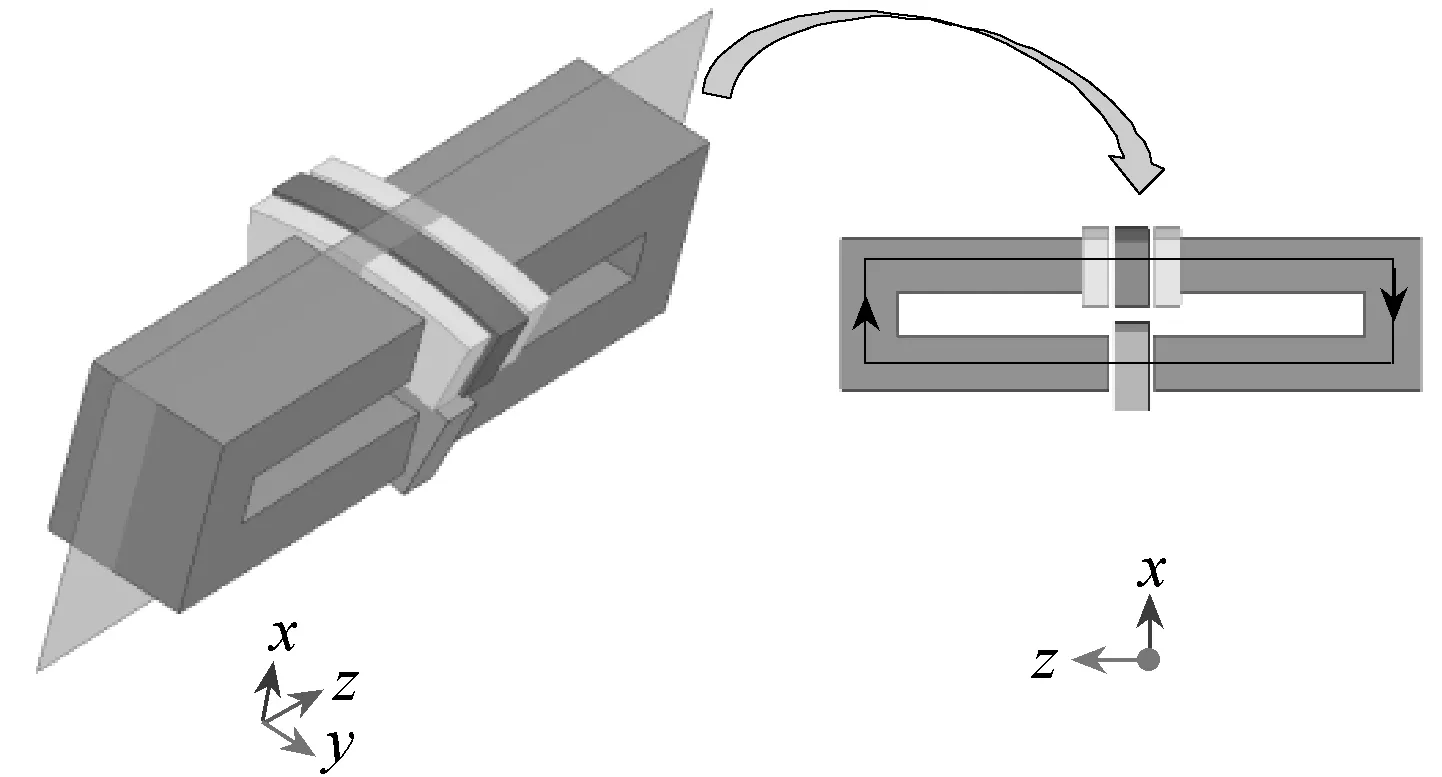
图2 DTFM主磁路Fig.2 Main magnetic circuit of DTFM

2 DTFM主要尺寸设计

DTFM的主要尺寸设计是电机电磁设计的基础研究内容，下面对该电机进行主要尺寸表达式的推导，图3为DTFM尺寸示意图。

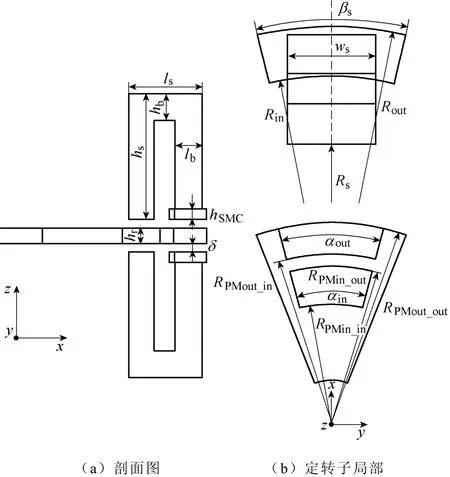
图3 DTFM尺寸示意图Fig.3 Dimension diagram of DTFM

由于电机原理结构特殊，在进行电机主要尺寸推导前首先对新型盘式横向磁通永磁无刷电机的电负荷A和电压系数ku进行定义。

考虑到新型盘式横向磁通永磁无刷电机结构的特殊性，定义其电负荷AL为

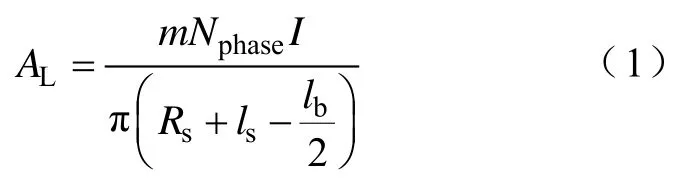
式中，I为电机相电流；m为相数；Nphase为一相串联匝数。

电压系数ku定义为

式中，E为电机空载反电动势；U为电机输入相电压。

如果只考虑DTFM基波分量可得到

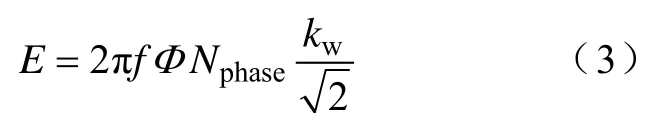
式中，Φ为轴向前后两块定子铁心对应主磁路的主磁通。

电机采用10极12槽结构，因此，f=np/ 60 =n/ 12，电机绕组系数kw= 0.965 9。

电机输出功率计算方程为

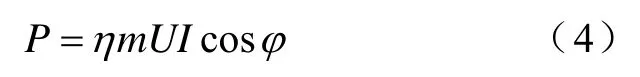
式中，η为电机效率；cosφ为电机功率因数。

将式（1）～式（3）代入到式（4）中，可得

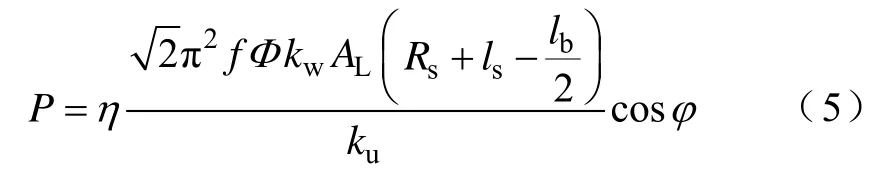
设DTFM定子铁心内径位置对应的气隙磁通密度幅值为Bδ2，可得到主磁通Φ为

定子铁心宽度ws可表示为

式中，ks为定子铁心宽度所对应的极弧系数。

定义定子铁心直径比γ为定子铁心在圆周方向排布时外径与内径之比，即

γ为电机尺寸设计过程中的重要参数。当盘式电机内径或外径给定时，可以通过优化γ得到最大输出功率。对于 DTFM，如果γ取值过小，则电机绕组导线空间小、绕线密集、电机电负荷过大，从而导致电机发热现象突出等问题；若γ取值过大，则电机外形尺寸容易超标或者电机内径空间过小，不利于放置轴承及制动器等配套器件，此外还会增加电机整体质量，削弱横向磁通电机转矩密度高的优势。对于中小型盘式电机，γ通常选取在1.5～1.7之间。对于本电机，在初始设计中，假定γ=1.6。

为保证电机定子铁心的绕线空间，定子铁心径向高度ls设定为

将式（6）～式（9）代入到式（5）中，可得

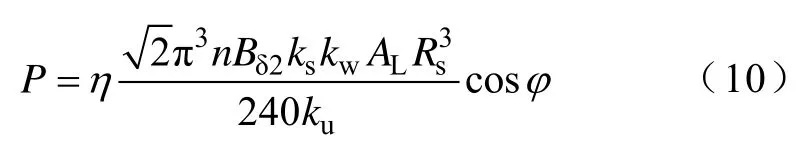
整理后可得

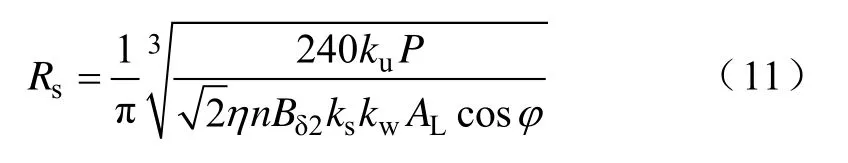
3 结构尺寸变化对电机性能的影响

电机的齿槽转矩以及额定条件下输出转矩是电机的关键性能指标，在电机主要尺寸已经确定的情况下，通过修改部分结构尺寸参数可以获得不同的电机输出效果，本研究选取定子极靴圆心角度βs、极靴厚度hSMC以及内外两块永磁体圆心角度αin和αout作为优化变量，这 4个变量对电机质量体积影响较小，但对电机齿槽效应及输出转矩影响较大。在分析单一参数变化对电机性能的影响以及后续进行优化设计时，这4个参数的初始值及优化取值范围见表1。

表1 变量初始值及优化取值范围Tab.1 Initial value and range of optimization variables

图4为电机输入额定电流（I=12.5A）条件下输出转矩的平均值以及电机空载条件下仿真得到的齿槽转矩峰峰值随外永磁体圆心角度αout变化的情况。随着外永磁体圆心角度增加，永磁体截面积增大，电机主磁路有效磁通量增加，电机输出转矩上升；齿槽转矩在αout=28°取得最大值，之后呈递减趋势。

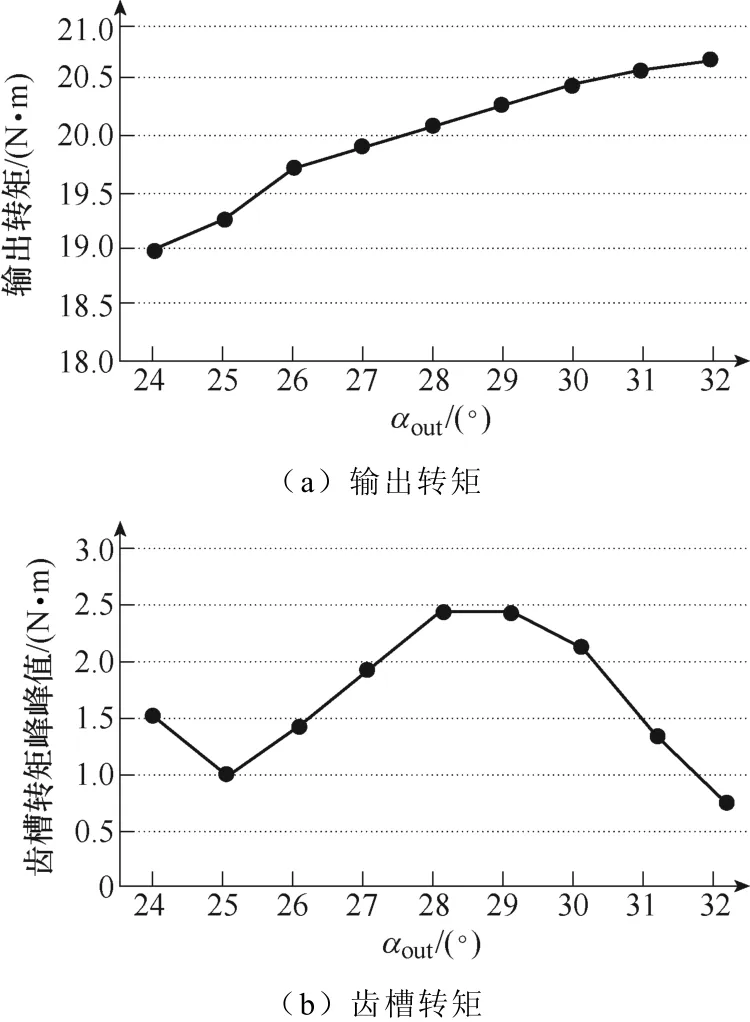
图4 输出转矩及齿槽转矩随αout变化曲线Fig.4 The curves about the output and cogging torque changing with αout

图5为电机输入额定电流（I=12.5A）条件下输出转矩的平均值以及电机空载条件下仿真得到的齿槽转矩峰峰值随内永磁体圆心角度αin变化的情况。随着内永磁体圆心角度增加，电机输出转矩基本呈上升趋势；齿槽转矩变化幅度较小。

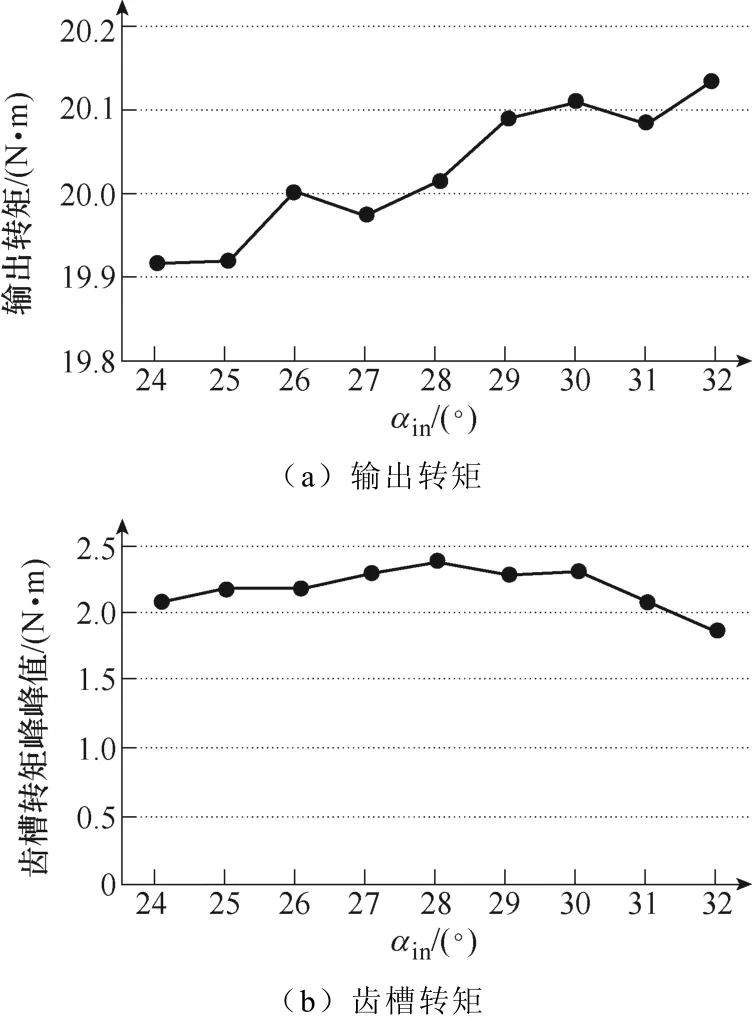
图5 输出转矩及齿槽转矩随αin变化曲线Fig.5 The curves about the output and cogging torque changing with αin

图6为电机输入额定电流（I=12.5A）条件下输出转矩的平均值以及电机空载条件下仿真得到的齿槽转矩峰峰值随定子极靴圆心角度sβ变化的情况。随着极靴圆心角度增加，电机输出转矩开始基本维持不变，当sβ达到24°后，输出转矩开始下降，究其原因，主要是由于极靴圆心角度进一步增加，极间漏磁增加，主磁路有效磁通下降；齿槽转矩在sβ=24°取得最大值，之后呈现递减趋势。

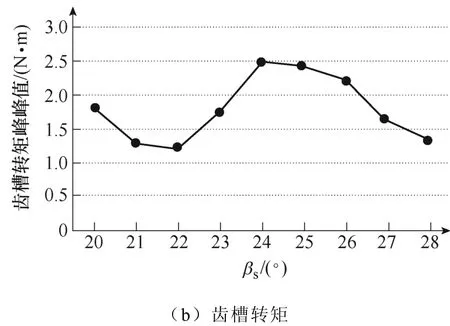
图6 输出转矩及齿槽转矩随βs变化曲线Fig.6 The curves about the output and cogging torque changing with βs

图7为电机输入额定电流（I=12.5A）条件下输出转矩的平均值以及电机空载条件下仿真得到的齿槽转矩峰峰值随定子极靴厚度hSMC变化的情况。随着极靴厚度增加，电机输出转矩呈缓慢下降趋势，主要原因是 SMC磁导率相对硅钢片低，厚度增加导致主磁路磁阻增加；齿槽转矩变化幅度较小。

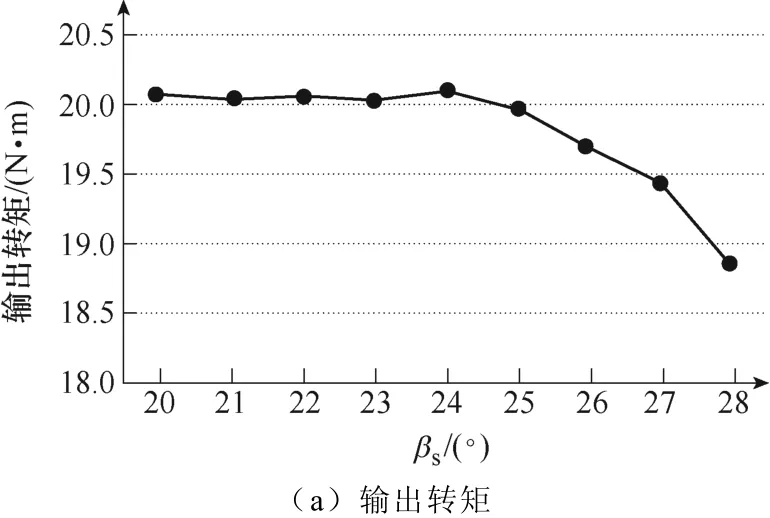
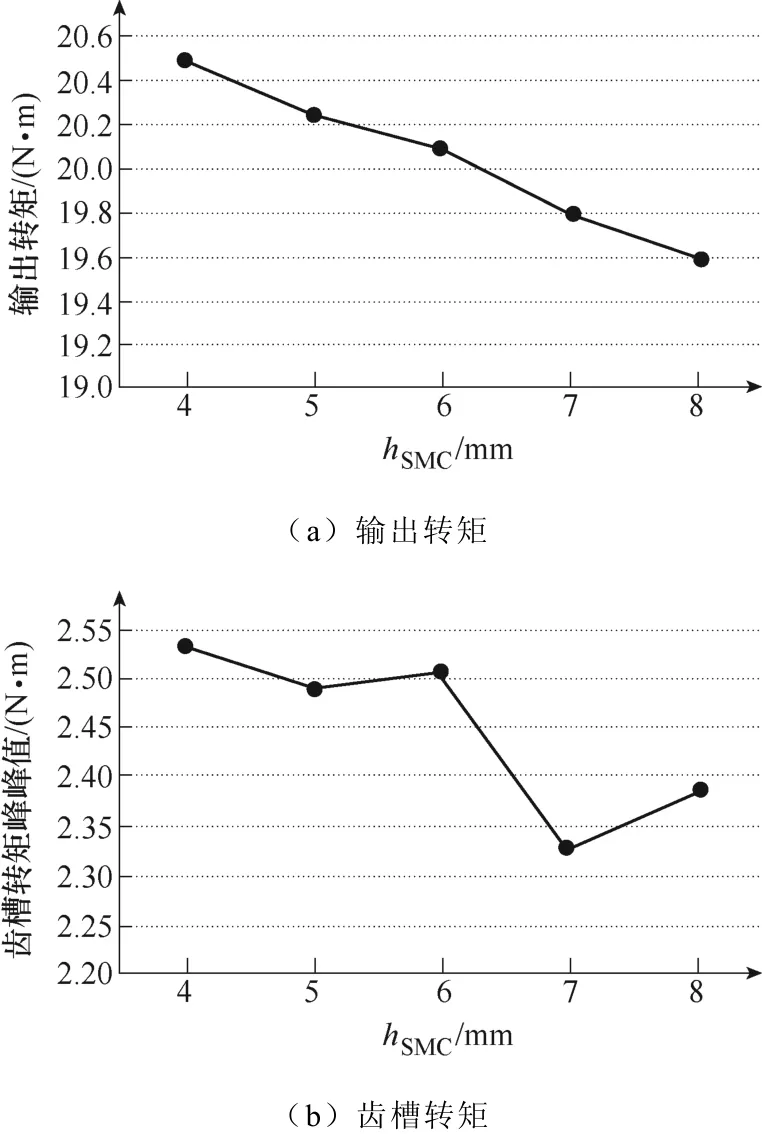
图7 输出转矩及齿槽转矩随hSMC变化曲线Fig.7 The curves about the output and cogging torque changing with hSMC

4 DTMF的全局优化设计

结合 BP神经网络非线性映射能力强、训练算法稳定可靠以及多目标粒子群优化（Particle Swarm Optimization, PSO）算法易于实现、精度高、收敛快的优点[15-16]，本文提出一种基于 BP神经网络和多目标PSO的新型优化策略。图8为这一新型优化策略的算法流程，其中，Pid和Pgd分别为个体最优粒子位置和全局最优粒子位置，在这一流程中，引入遗传算法对神经网络的训练进行优化，以弥补普通神经网络算法学习速度慢、收敛时间长、容易陷入局部极小值、网络推广能力弱[17]等缺陷。

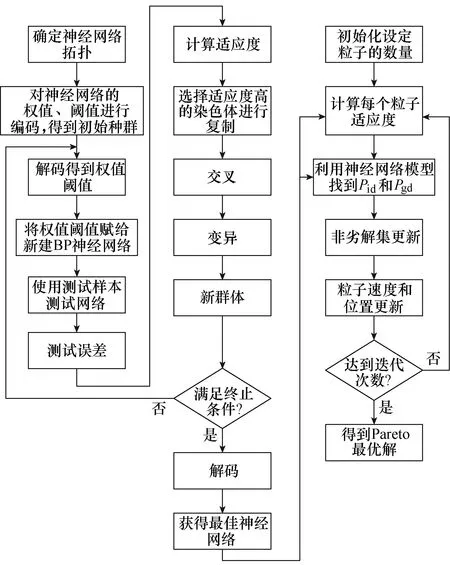
图8 新型优化策略算法流程Fig.8 The procedure of new optimization strategy

该优化策略具体步骤如下：

（1）利用正交试验法获得优化变量和对应的电机输出效果，组成试验样本。

（2）根据试验样本，建立优化变量和优化目标的神经网络预测模型，神经网络训练过程结合遗传算法。

（3）应用多目标PSO获得待求解问题Pareto最优解，在此过程中利用神经网络模型估计目标函数值。

四因素五水平见表2，是为神经网络建立提供的训练样本，为了保证 BP神经网络的精确性，每组训练样本对应的电机输出效果需要通过3D-FEM进行计算得出。

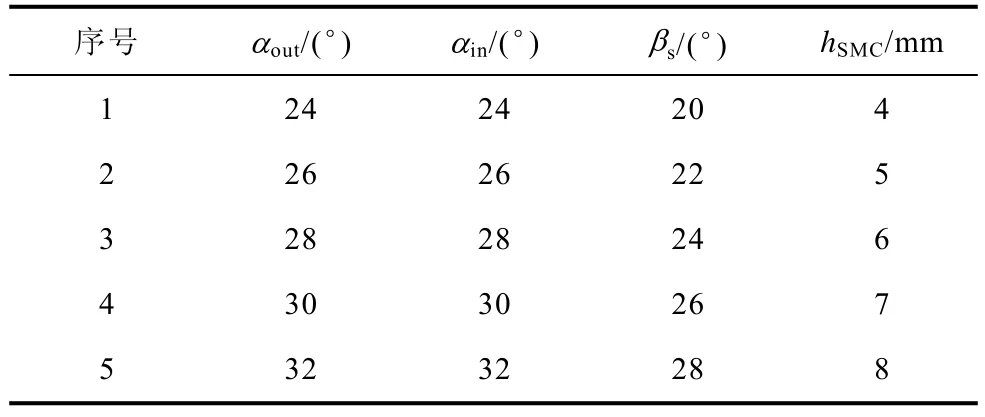
表2 四因素五水平Tab.2 Four factors and five levels

按照四因素五水平表，总样本数为625个，整个仿真过程耗时较长，占用过多计算资源，为了尽可能缩短仿真过程，拟采取正交试验设计方法。表3是本次试验设计用到的L25正交试验，每组试验对应的仿真结果在表中给出。

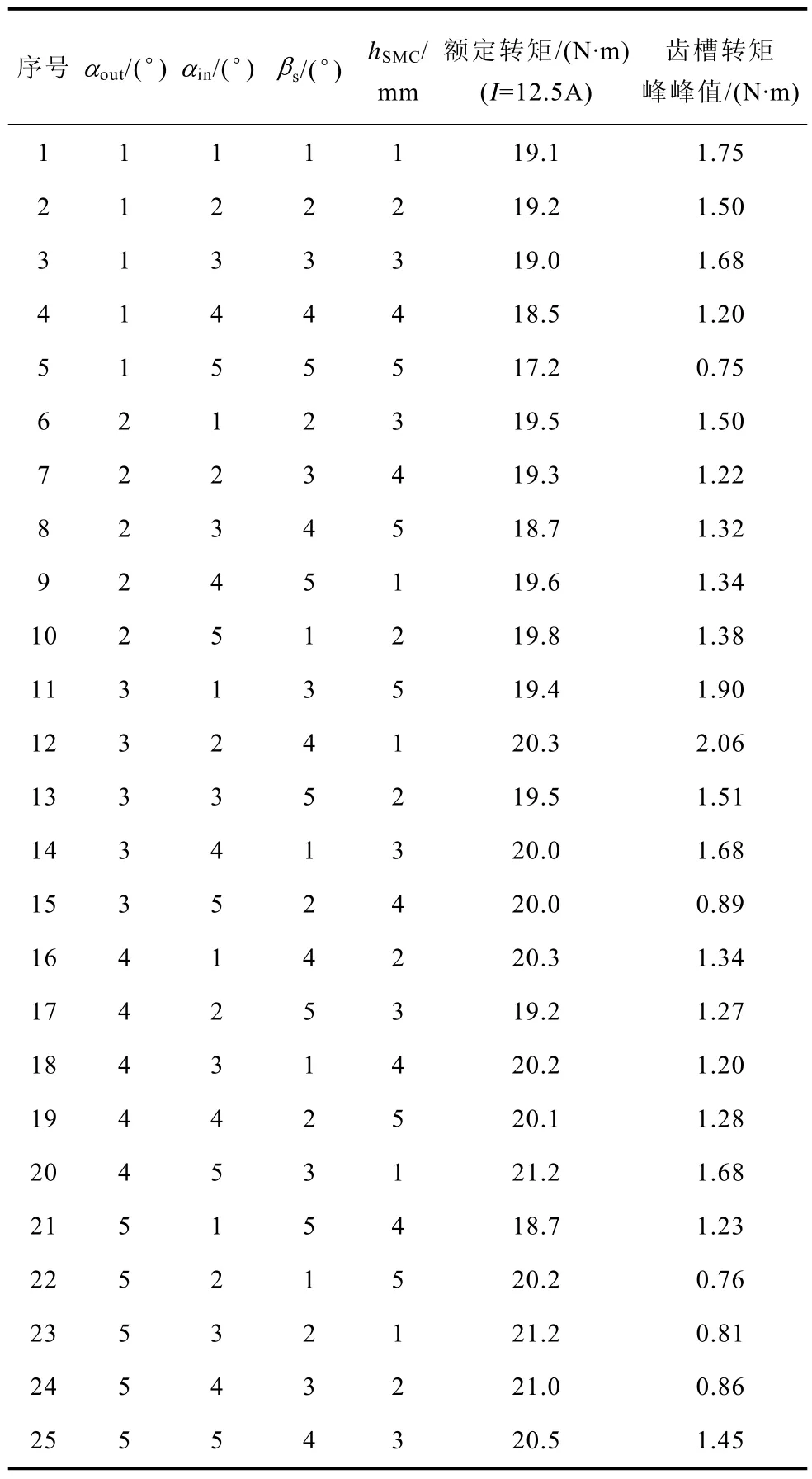
表3 L25 正交试验Tab.3 L25 orthogonal experiment

将表3内 25组仿真数据作为神经网络训练样本，另选取3组仿真数据作为测试样本，见表4。

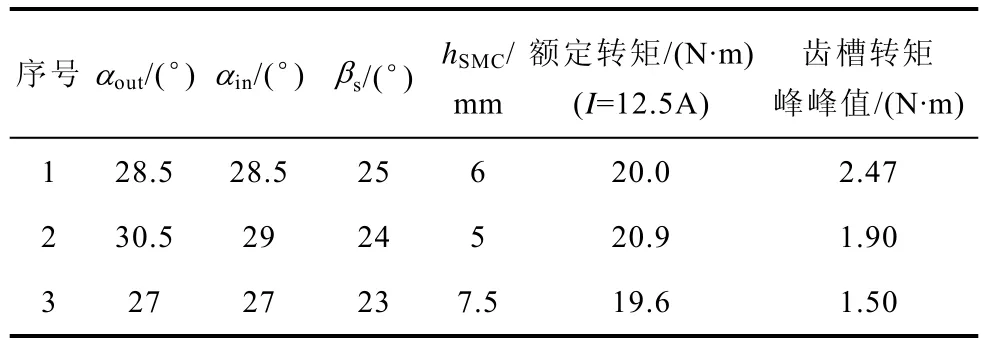
表4 测试样本数据Tab.4 The data of test samples

表3的25组试验数组作为训练样本，表4内3组试验数组作为测试样本，以此来训练 BP神经网络，考虑到 BP神经网络的局限性，引入遗传算法对神经网络的训练进行优化。优化后的 BP神经网络作为预测模型用于拟合优化变量和输出的优化目标值之间的函数关系。最后，以电机的齿槽转矩Tcog最小以及额定电流输出转矩Tout最大为优化目标对电机进行优化，其具体问题可以归结为

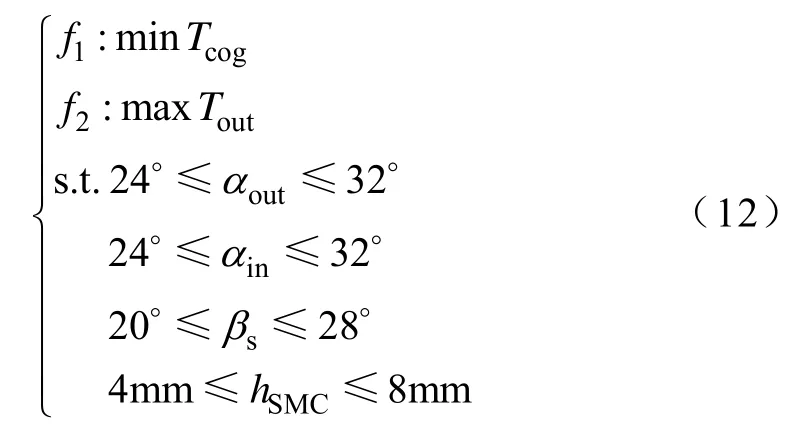
多目标PSO算法给出初始粒子群，一组优化变量作为一个单独的粒子，再通过 BP神经网络计算出每个粒子对应的电机输出效果从而得到适应度值，根据各粒子适应度值，选出非支配粒子，在粒子群迭代过程中，非支配粒子不断更新，最终经过N次迭代得到Pareto最优解集。图9为50次迭代后得到的Pareto最优解。

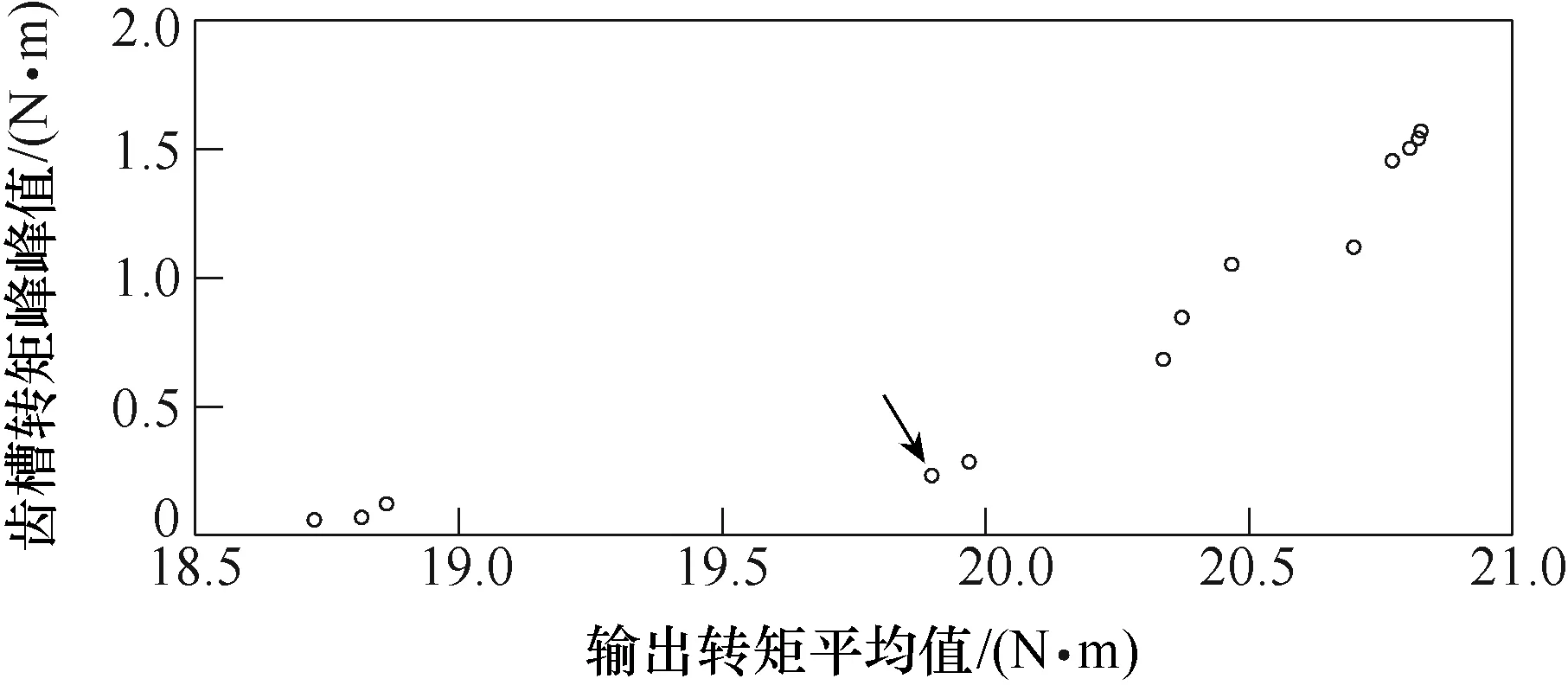
图9 Pareto最优解Fig.9 Pareto optimal solutions

通过多目标PSO最终得到的Pareto最优解共有 13个，其中，3个最优解输出转矩平均值小于18.9N·m，但是具有更小的齿槽转矩，另有部分最优解输出转矩平均值较高，部分接近21N·m，但是其齿槽转矩也较高。综合考虑，选取图9中箭头所指粒子为该优化设计的最优解，该粒子对应的齿槽转矩峰峰值为0.23N·m，输出转矩平均值为19.90N·m，对应的优化变量取值为αout= 3 1.5°，αin=28.5°，βs=25.3°，hSMC= 4.1mm。

针对优化设计后得到的电机参数，利用有限元软件进行建模仿真，得到优化后电机模型有限元仿真结果。将电机初始模型仿真结果与优化后模型进行对比，以检验电机优化设计过程。图10和图11分别为初始电机模型和优化后电机模型齿槽转矩波形和额定电流（I=12.5A）条件下输出转矩波形的对比。通过优化设计，齿槽转矩峰峰值由优化前的2.07N·m下降到0.24N·m，输出转矩平均值优化前为20.07N·m，优化后为20.06N·m，基本保持不变。将有限元仿真得出的优化后电机模型仿真结果与根据新型优化策略拟合出的电机模型输出结果进行比较，两者差距较小，进而验证了优化策略的可靠性和可信赖度。

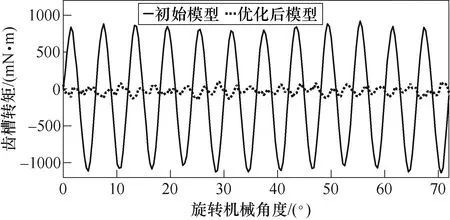
图10 齿槽转矩对比Fig.10 Comparison of cogging torque

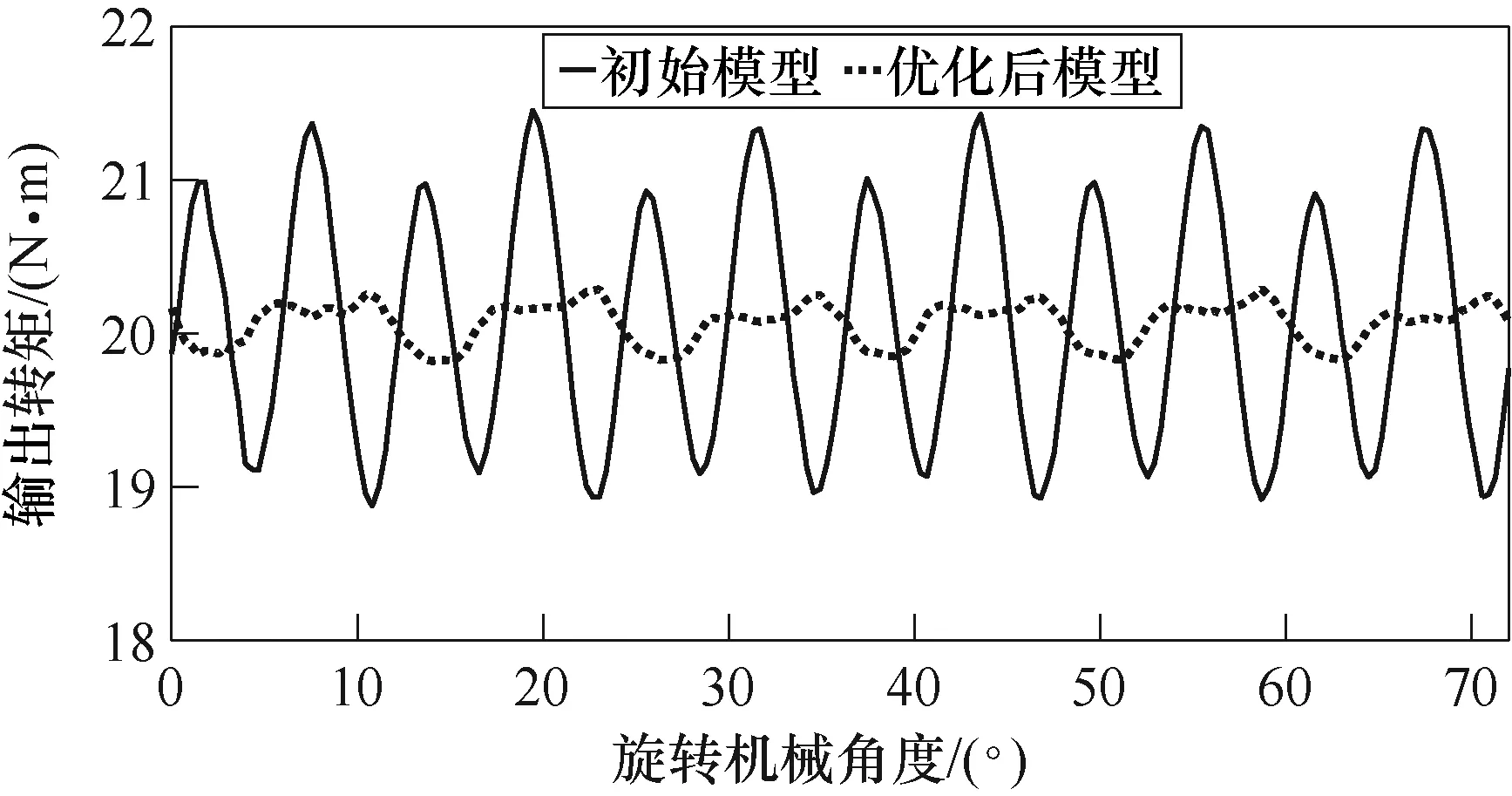
图11 额定电流下输出转矩对比Fig.11 Comparison of output torque under rated current

5 DTFM样机及实验

本文试制了一台DTFM样机进行实验检测。图12所示为DTFM定子和转子部件实物。

图12 DTFM部件实物Fig.12 Practicality pictures of DTFM components

图13为在3 000r/min转速下，测得的A相反电动势波形，可以看出，该电机具有良好的永磁相电动势波形正弦性，实验测试结果相比于有限元仿真结果存在一定程度下降，主要原因是电机制作过程中定子铁心硅钢片和 SMC极靴结合部分存在一定气隙，电机实际气隙增大。为了测试电机动态性能，在电机空载条件下，对电机起停机过程进行跟踪测试，测试过程中驱动器控制电机加速到3 000r/min后开始停机。图14为通过工控机检测到的电机转速变化以及电流信号变化曲线，图15为示波器检测到的动态过程电流包络线，通过动态过程曲线，可以得出，电机起动和停机过程时间基本相同，均在2s左右，样机具有较好的动态性能。

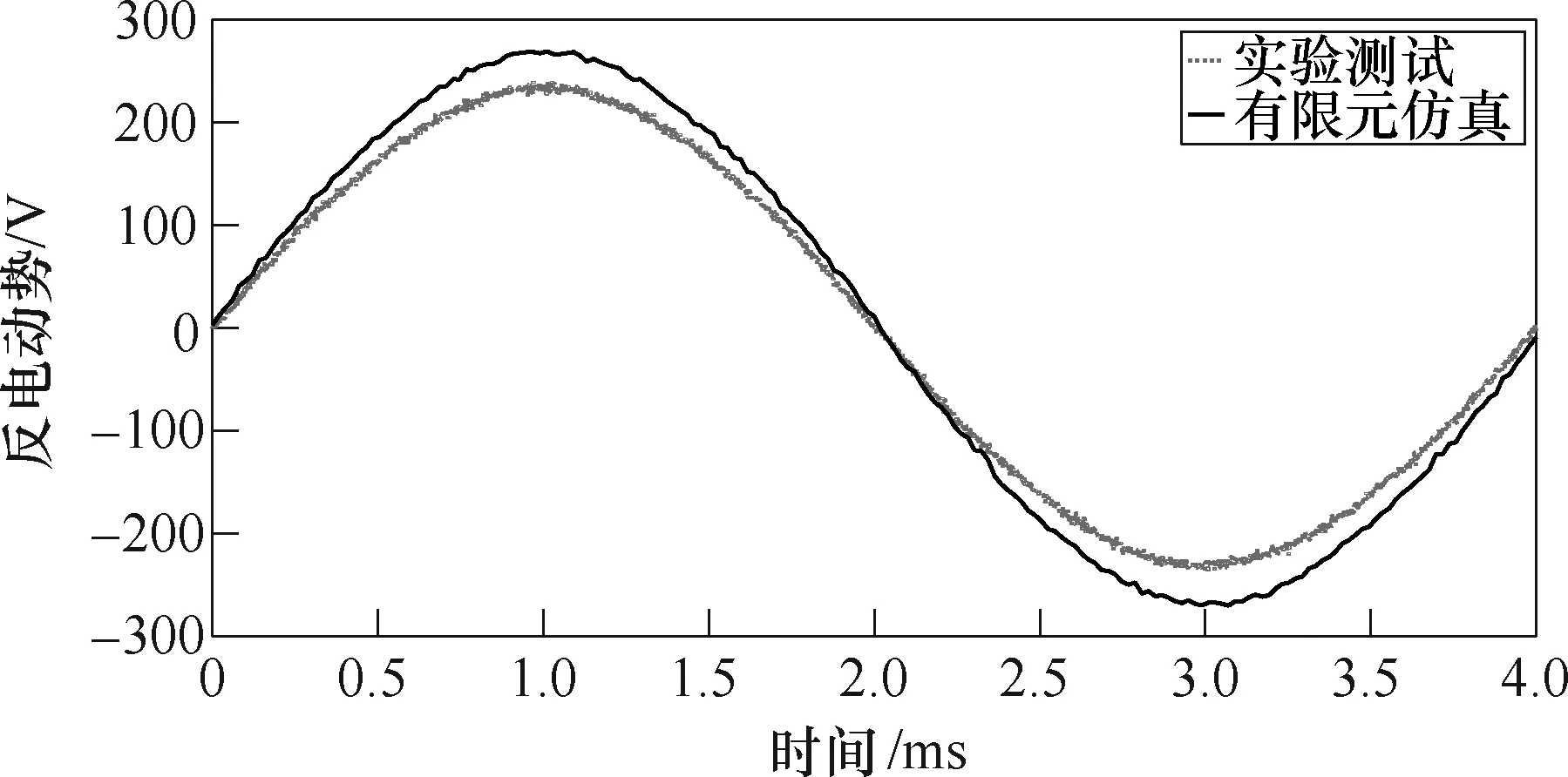
图13 3 000r/min转速下电机空载发电反电动势Fig.13 Measured no load back-EMF at the speed of 3 000r/min

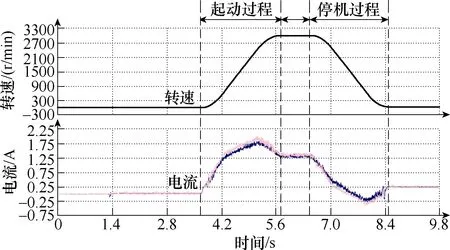
图14 电机转速及电流跟踪曲线Fig.14 Position and current tracking curves of motor

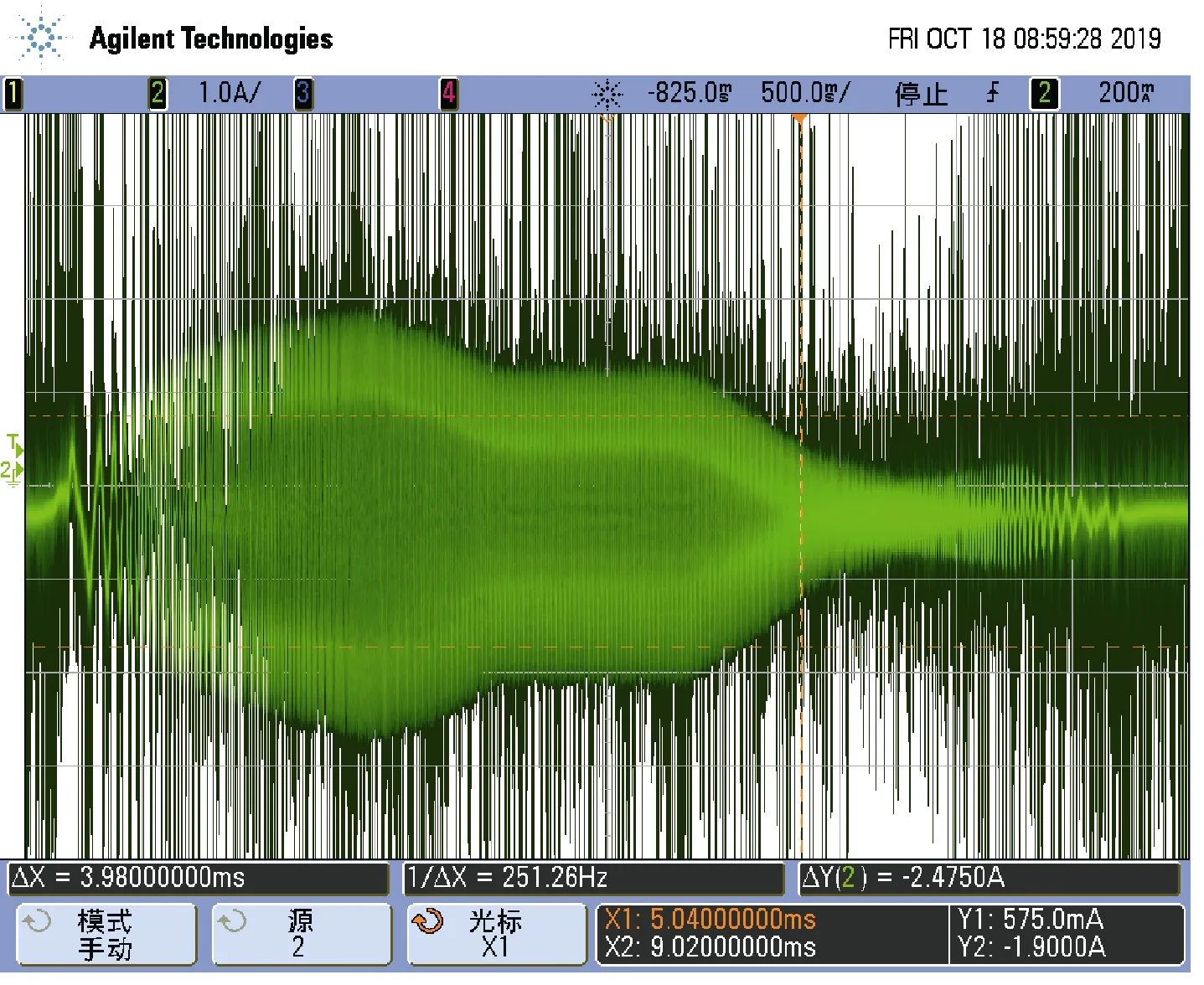
图15 动态测试电流包络线Fig.15 Envelope curve of current obtained by dynamic test

为了验证电机负载条件下性能，搭建了如图16所示的负载实验平台。整个实验平台包括样机、磁滞测功机、测功机控制柜以及配套上位机、驱动器、用于给电机制动器和驱动器低压模块供电的稳压直流电源和向驱动器发出控制指令的工控机。

图16 负载实验平台Fig.16 Platform of load experiment

电机采用Id=0控制方法，图17为通过实验测得的电机输出转矩与交轴电流Iq的对应关系。通过实验结果可以看出，在额定电流 12.5A，电机输出转矩与第4节优化后电机仿真结果存在差距。在样机制作过程中，为了保证线圈能够方便套入定子铁心，在硅钢片上进行倒角加工，导致铁心截面积下降，铁心饱和程度提高，此外，反电动势的下降原因也会造成样机输出转矩的下降。图18为根据电机实验结果整理的效率 MAP图，电机最高效率为90%，在额定转速3 000r/min和额定转矩20N·m下，电机效率约为82%（包括驱动器效率）。

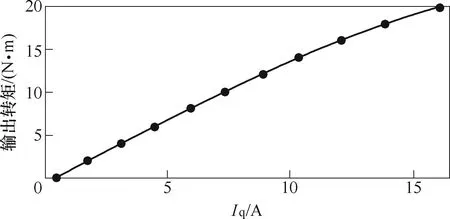
图17 转矩-电流关系曲线Fig.17 Torque-current curve

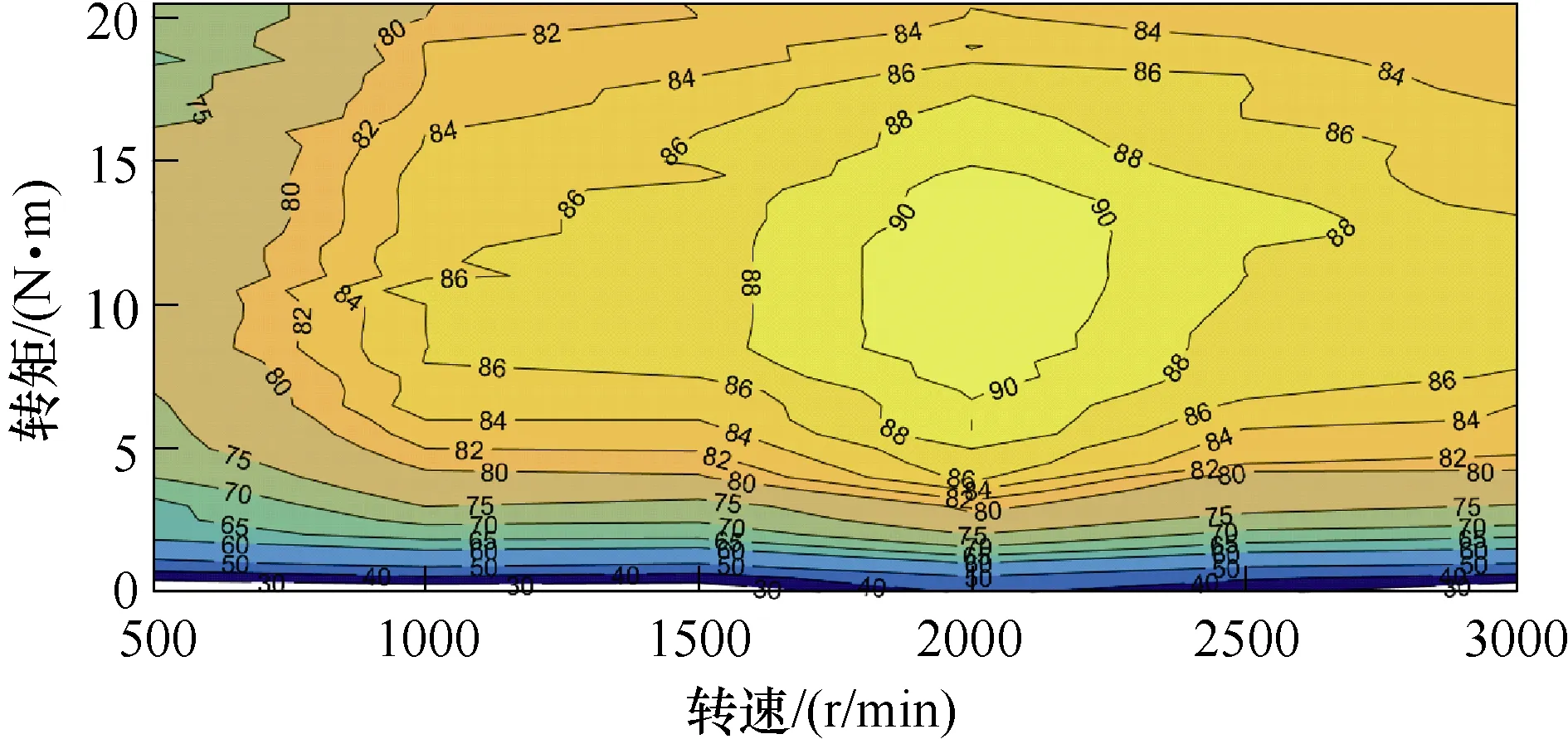
图18 电机效率MAP图Fig.18 Efficiency MAP of motor

根据DTFM样机的实验结果，选取了一台同功率普通径向磁场永磁无刷伺服电机市场产品进行对比分析。图19所示为两台电机的外观对比，表5进一步给出了两台电机的性能及尺寸对比情况。本文设计的DTFM样机具有明显的尺寸及质量优势，轴向长度缩小了40.8%，电机质量降低了21.9%，同时转动惯量下降了54.2%，因此具有更好的动态性能。

图19 DTFM样机与市场产品对比Fig.19 Comparison between DTFM prototype and market product

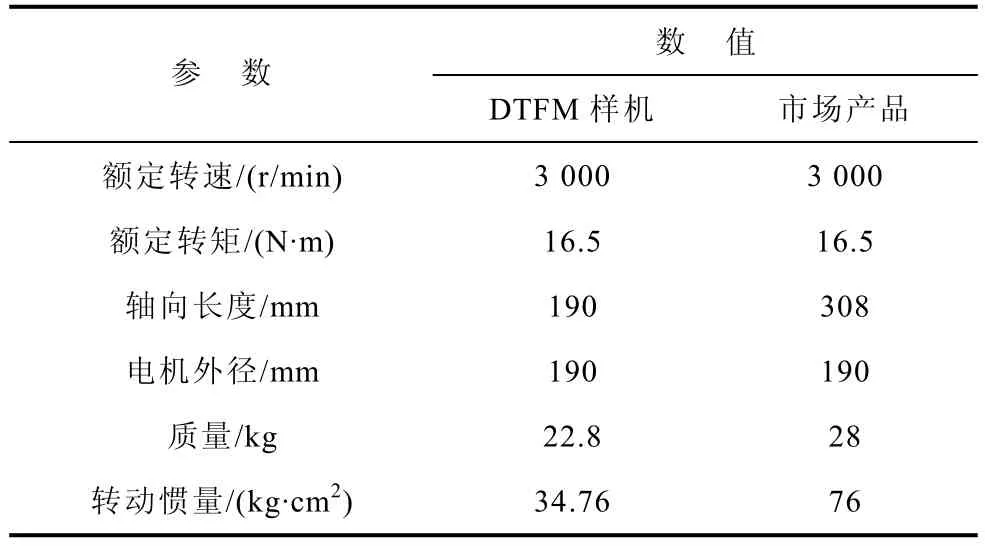
表5 电机性能及尺寸对比Tab.5 Comparison of performance and size of motors

6 结论

本文提出了一种应用于工业机器人的新型盘式横向磁通永磁无刷电机，结合横向磁通电机和盘式电机的特点，具有轴向长度短、动态性能好的优点，电机定子采用分块电枢结构，降低了电机各相之间的耦合度，更有利于伺服电机的控制。通过推导DTFM主要尺寸公式完成了DTFM的初步电磁设计计算。采用单一变量法分析了永磁体和定子极靴参数变化对齿槽转矩和额定输出转矩的影响，并采用新型优化策略对电机进行多目标优化，优化后的结果显示，电机在保持较高输出转矩的同时齿槽转矩明显降低。最后，通过样机实验对DTFM电机各项性能进行测试，并与某型号同功率市场产品进行对比，比较结果显示，DTFM电机在轴向尺寸以及转动惯量等方面具有明显优势。