基于PID型代价函数的永磁同步电机模型预测电流控制

陈卓易 屈稳太

（浙大宁波理工学院信息科学与工程学院 宁波 315100）

0 引言

永磁同步电机（Permanent Magnet Synchronous Machine，PMSM）具有功率密度大、效率高等优点，在高性能电驱动场合得到广泛应用。围绕如何进一步提高控制性能而涌现出的各种先进控制算法中，PMSM电流有限集模型预测控制（Finite-Control-Set Model Predictive Control, FCS-MPC）[1-3]近年来逐渐成为热门。该控制方法继承了磁场定向控制的思想，将PMSM电流分解为控制磁链的d轴电流和控制转矩的q轴电流，因此，转矩控制和弱磁扩速等目标均可归结为对d、q轴电流的高性能控制。FCS-MPC电流控制由于无需调制器而直接控制开关器件，具有动态响应快的优点，此外，还具有原理直观、设计灵活、多目标容易协同等优点[1]，但同时也具有依赖模型参数的缺点[2]。模型参数失配会导致电流稳态误差和纹波增大、控制性能降低。实际应用中，PMSM参数未必能精确获得，其电阻、磁链或电感等参数也会随着温升或磁路饱和程度的变化而变化[3]，因此，FCS-MPC电流控制的参数敏感性问题亟待解决。

为解决 FCS-MPC的参数敏感性问题，基于参数辨识的方法[3-5]通过在线辨识PMSM的各种参数，实时调整预测模型，提高电流预测精度，从而在电机参数未知或时变的情况下得到良好的电流控制性能。然而，PMSM参数众多，同时辨识所有参数会导致欠秩问题[4]，所以一般只能针对其中几个变化较大或较关键的参数进行辨识[5]，并且其辨识精度依赖于待辨识参数以外模型的精度，因此，饱和、逆变器死区、管压降等不容易考虑在模型中的非线性因素[6]使得参数辨识的方法实际上很难精确。

基于扰动观测的方法[7-9]则是对各种参数误差以及逆变器非线性等各种内外扰动所产生的总扰动进行在线观测和补偿。这类方法能解决待辨识参数过多的问题，而且考虑了未建模的非线性扰动[7]，但是复杂的观测器和参数辨识算法一样，容易加重控制器的运算负担，提高控制系统的成本。此外，以总扰动方式处理模型失配，一般只降低电流稳态误差，而不能改善电感参数不准而增大的纹波误差[8]，需要额外对电感误差进行补偿[9]。

另有研究主张采用无模型FCS-MPC[10-11]，直接由不同电压矢量对应的电流变化率进行电流预测，从而无需依赖电机参数。但是，该方法增加了对电流采样精度和时序的要求，同时还存在变化率更新停滞的问题[11]。

以上方法均是针对 FCS-MPC的改进，即通过提高预测准确度来提高参数未知或时变场合的控制性能。预测是 FCS-MPC实现控制的第一步，而直接决定控制量的则是代价函数，因此，通过代价函数的改进[12-13]理论上也可提高电流控制性能。然而目前对代价函数的研究一般围绕多目标协同[13-14]的主题，而且这些方法多以参数匹配为前提，因此并未涉及参数敏感性问题。

为改善FCS-MPC在PMSM电流控制中的参数敏感性，本文提出一种比例-积分-微分（Proportion-Integration-Differentiation, PID）型代价函数，在预测模型参数失配时能改善电流控制性能。一方面，通过积分误差代价消除稳态误差；另一方面，通过微分误差代价降低电流纹波误差，在较大参数变化范围下均能实现高性能电流控制，同时保留FCS-MPC动态响应快的优点。

1 永磁同步电机FCS-MPC电流控制

FCS-MPC实现PMSM电流控制的过程可概括为：在所有可能的逆变器开关组合下，根据由PMSM模型建立的预测模型得出未来的预测电流，并用表征控制目标（如给定电流的跟踪）的代价函数对每个预测电流进行评估，能使代价函数取最小值的开关组合即为控制器的下一拍输出。

1.1 预测模型

PMSM的dq坐标系下的定子电压方程为

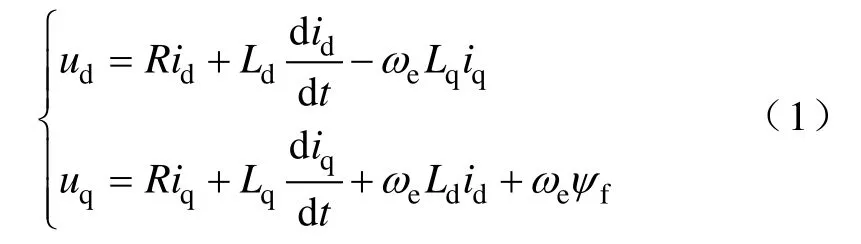
式中，id、iq分别为 d、q轴定子电流；R为定子电阻；ψf为转子永磁体磁链；ωe为转子电角速度；Ld、Lq分别为 d、q轴电感；ud、uq分别为 d、q轴定子电压，可由αβ 坐标系下电压uα、uβ由 Park 变换

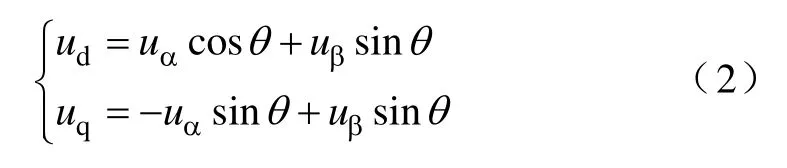
得到，其中，θ为转子电角度。在不考虑死区和管压降等非理想特性时，三相两电平逆变器的uα、uβ可以根据逆变器开关状态Sabc从表1查得，其中，UDC为直流母线电压。

表1 开关状态表Tab.1 Switching table

用欧拉法对式（1）在第k时刻离散化，得预测模型为

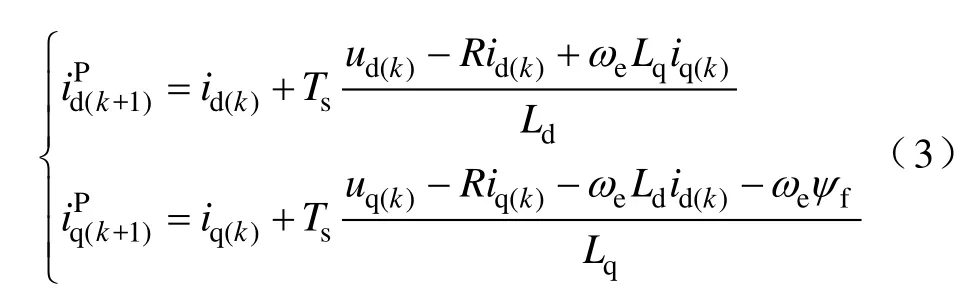
式中，上标P为预测值；Ts为采样周期。然后用式（3）由k时刻输出电压、采样电流以及系统参数推算出k+1时刻的d、q预测电流，称为单步预测。微控制器实现时常用两步法[15]来补偿程序执行延时。k时刻先输出上周期优化得到的开关状态，并用式（3）计算出一对并通过

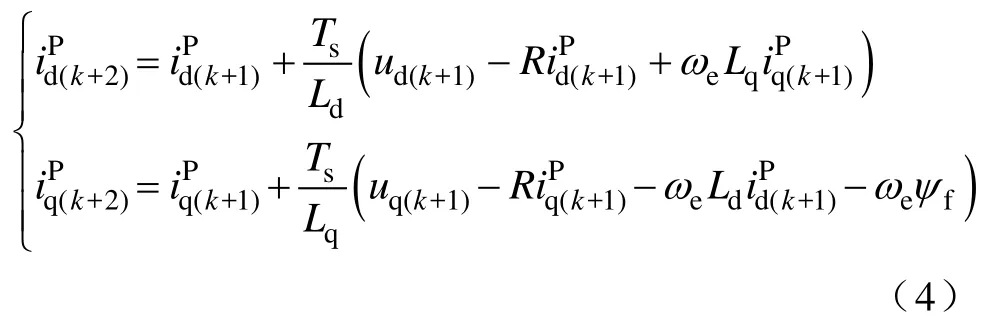
可分别预测不同Sabc作用下k+2时刻的电流，这也属于单步预测。由于多步预测模型与单步预测一样基于电机数学模型，因此仅讨论单步预测的情况。

电机电流是否能被准确地预测，与模型的精确程度有关。不同工况下电机磁路饱和程度不同，会造成电感随着饱和程度的变化而变化。R和ψf也会随着温度变化而时变。此外，高次谐波、逆变器非线性等因素也难以在传统预测模型中精确计及，会造成一定的预测误差。

1.2 传统代价函数

与采用脉冲宽度调制（Pulse Width Modulation，PWM）来分配开关占空比不同，FCS-MPC不使用调制器而直接输出下一时刻的开关状态。对于下一时刻所有可能的开关状态，均可由表1以及式（2）计算出对应的定子电压ud、uq，并由式（4）计算出预测电流。又由外环得到的电流指令根据传统代价函数式（5）计算能使代价函数J最小的其对应的开关状态即最优控制量，将在下一时刻输出。

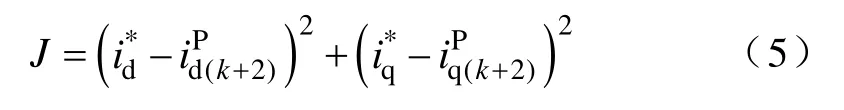
可以看出，传统的给定跟踪型代价函数的目标是选出能使预测电流矢量与参考电流矢量欧氏距离最短的点，即控制误差最小的点，但并未考虑预测电流的准确度以及电流控制误差的累计，因此不能保证稳态无差以及最佳的纹波抑制，尤其是在预测模型并不准确的时候。

2 基于PID型代价函数的FCS-MPC

为解决预测模型不精确造成控制误差的问题，本文提出一种PID型代价函数。其思想是从常用的负反馈控制器——PID控制器中得到启发：积分环节可以消除稳态误差，因此对 FCS-MPC历史控制误差作积分，得到积分误差代价，旨在消除静态误差；微分环节能预测误差变化的趋势，因此设计微分误差代价，对单位电流变化引起的预测误差进行补偿；而传统代价函数中预测电流与参考电流之差，则可看作比例误差代价，其功能类同于PID中的比例环节。本节将具体阐述 PID型代价函数及其在PMSM电流FCS-MPC控制中的实现。

2.1 积分和微分误差代价

PID控制中，控制输出y为比例项P、积分项I和微分项D之和，其中，积分项I的后向差分格式为

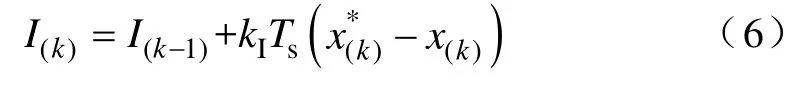
式中，x为被控变量；x*为给定值；kI为积分增益系数。在y中加入积分项I可以使x稳态无差。类似地，对电流控制误差也进行积分，得到

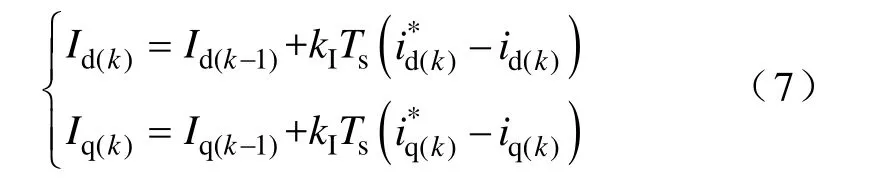
式中，Id和Iq分别为d、q轴电流积分误差代价，由每个采样时刻的电流控制误差积分得到。在代价函数中加入该项，可以惩罚使积分误差代价继续增大的控制输出，从而使累计控制误差趋于零。

采用积分误差代价理论上能完全消除稳态控制误差，但由于 FCS-MPC的开关离散性，电流达不到真正意义上的稳态[8]，因此模型误差引起的每一拍的控制误差仍可能存在，仅仅是误差均值为零。所以有必要引入微分误差代价，对每一拍的控制误差也进行补偿。

消除了稳态误差之后，纹波误差主要由对电流变化率的预测不准所致，例如，低估电感量或高估电机相电压均会导致高估电流变化率而引起预测误差，但该预测误差的大小和方向会随着电压矢量不同而不同，所以无法通过积分平均的方式来消除。此外，由于控制量不连续，无法采用传统PID中的微分项进行瞬态预测。因此，从纹波误差产生的原理出发，将每周期单位变化电流引起的预测误差作为微分误差代价的系数D′，得到

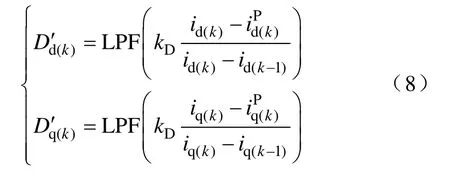
式中，kD为微分增益系数；LPF为低通滤波器函数。采用一阶低通滤波时，对于d轴有

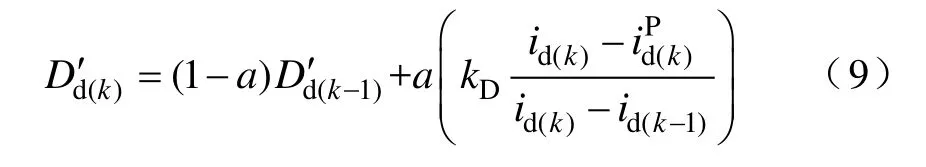
式中，a为0～1的滤波器系数。最终，d轴微分误差代价为系数D′与预测电流变化量的乘积，有

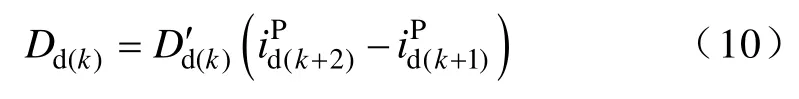
另外，为防止分母接近零而造成微分误差代价估计不准确，设置阈值ε，当电流变化率过低时不更新D′，有

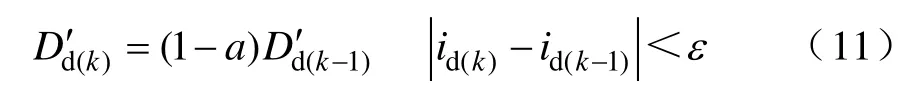
q轴微分误差代价的设计同式（9）～式（11）。

引入积分和微分误差代价后的代价函数，即PID型代价函数，有

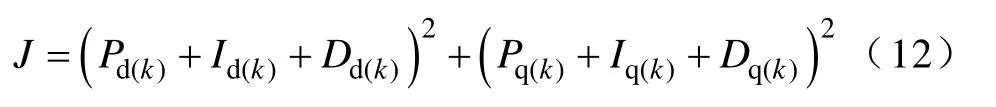
式中，P为传统代价函数中的电流误差项，有

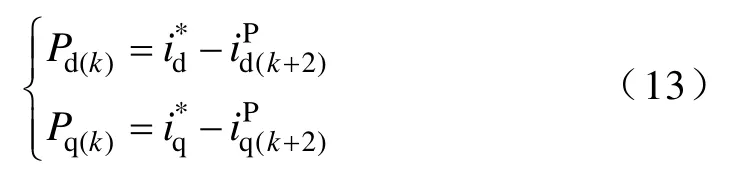
可认为是比例误差代价。其他 FCS-MPC应用中，如转矩和磁链参考值跟踪等，若以预测值和参考值之差作为代价，也可归类为比例误差代价。

2.2 采用PID型代价函数的FCS-MPC

采用 PID型代价函数的 FCS-MPC（以下简称PID-MPC）系统框图如图1所示，其中，电流给定值来自速度外环。相比于传统 FCS-MPC，仅改变了代价函数以及增加了虚线框内积分和微分误差代价运算部分，尽可能地保留了FCS-MPC的特点。

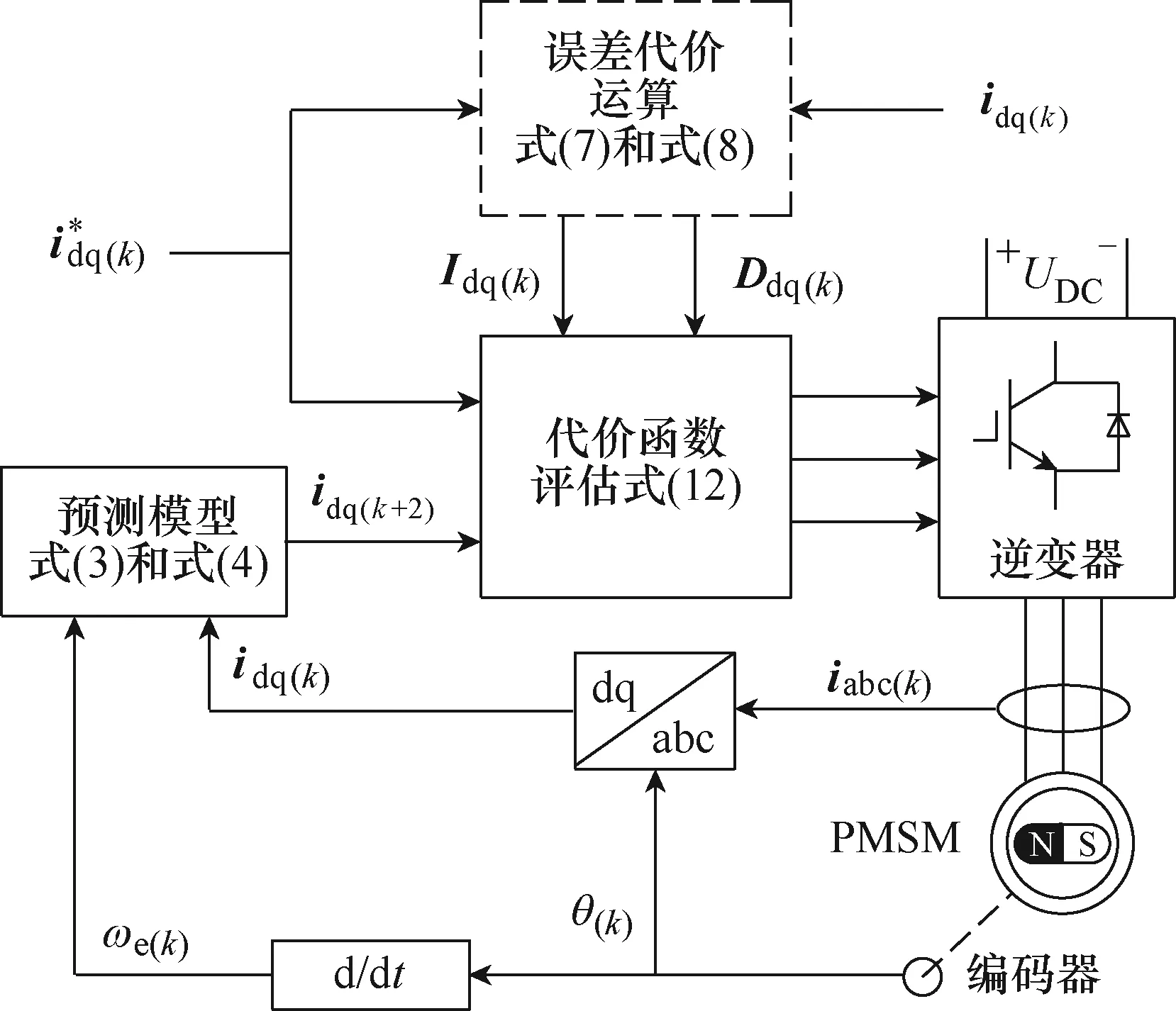
图1 PID-MPC系统框图Fig.1 Block diagram of proposed PID-MPC

若设置D为零，则简化为 PI型代价函数，仅消除电流稳态误差，而不抑制纹波。采用PI型代价函数的FCS-MPC以下简称PI-MPC。传统代价函数可认为是I、D均为零的特殊形式，即 P型代价函数，因此传统FCS-MPC以下简称P-MPC。

应当指出，PID型代价函数与PID控制器具有相似之处。积分误差代价与PID积分环节均是对历史控制误差作积分，而微分误差代价与PID微分环节均通过历史数据来预见未来误差变化。PID控制器常见的改进措施，如积分限幅等，也可以在 PID型代价函数中采用。但两者的作用机理不同，PID型代价函数最终通过对最优开关状态的选择来影响控制决策，而PID控制器则直接输出控制量。

采用PID型代价函数后，相比于传统FCS-MPC只需要多调节kI、kD和a3个系数（若只采用PI型代价函数，则只需多调节kI一个系数），然而可以免去对电机系统精确模型的测量工作（如描绘电感随电流变化的查表、逆变器死区补偿等），而且已包含参数随温度变化而时变的情况。3个系数的调节方法如下：增大kI可以降低电流稳态误差消除的响应时间，但过大kI会造成积分项I不稳定。在PMSM电流控制中，dq轴模型误差的直流扰动并无太多突变的情况，所以kI实际上无需设置过大。kD=1时能完全补偿微分误差，但由于采样噪声存在，完全补偿反而会造成更大的电流波动，所以，一般在 0＜kD＜1调节至合适值。低通滤波器系数a则可以根据实际系统的采样噪声适当增减。

3 实验结果

为验证PID型代价函数对电流控制误差的抑制作用，对一台三相PMSM进行控制实验。控制器以TMS320F28335为核心，负载采用电涡流制动器，两电平三相逆变器使用三菱IGBT模块CM300DX-24S1搭建。实验系统参数见表2。表贴式PMSM手册仅给出额定电感值Ls，因此，实验中Ld、Lq均以Ls为额定值。

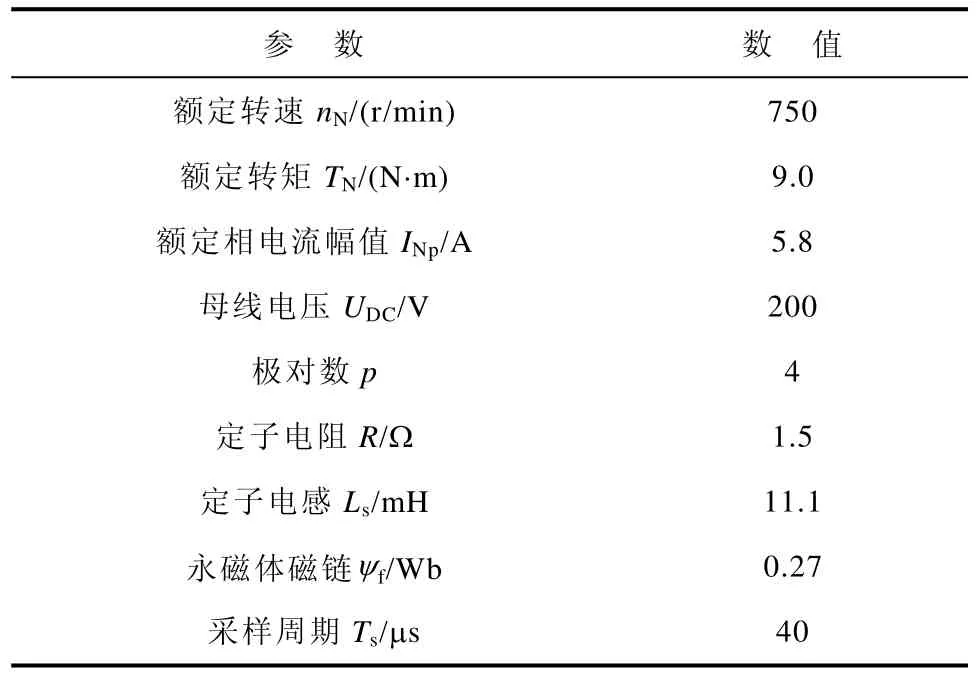
表2 系统参数Tab.2 System parameters

设置4个实验组如下：①采用传统代价函数和额定参数的 P*-MPC；②采用传统代价函数和与额定值不匹配参数的P-MPC，具体参数设置在每个实验中描述；③与P-MPC相同参数的PI-MPC；④与P-MPC相同参数的PID-MPC。

在PI-MPC中，设置kI=25；在PID-MPC中，设置kI=25，kD=0.8，a=0.000 5，阈值ε=0.01A。各组均采用相同参数的速度外环PI控制，电流内环为FCS-MPC，且=0。

图2为额定转速750r/min、额定负载转矩9N·m的情况下，4个实验组电流控制性能的对比实验。P-MPC、PI-MPC、PID-MPC的预测模型中电感、电阻、永磁体磁链均为150%额定值。每隔2s轮换实验组。图中，Eav和ERMS分别为电流平均控制误差和方均根控制误差，定义为

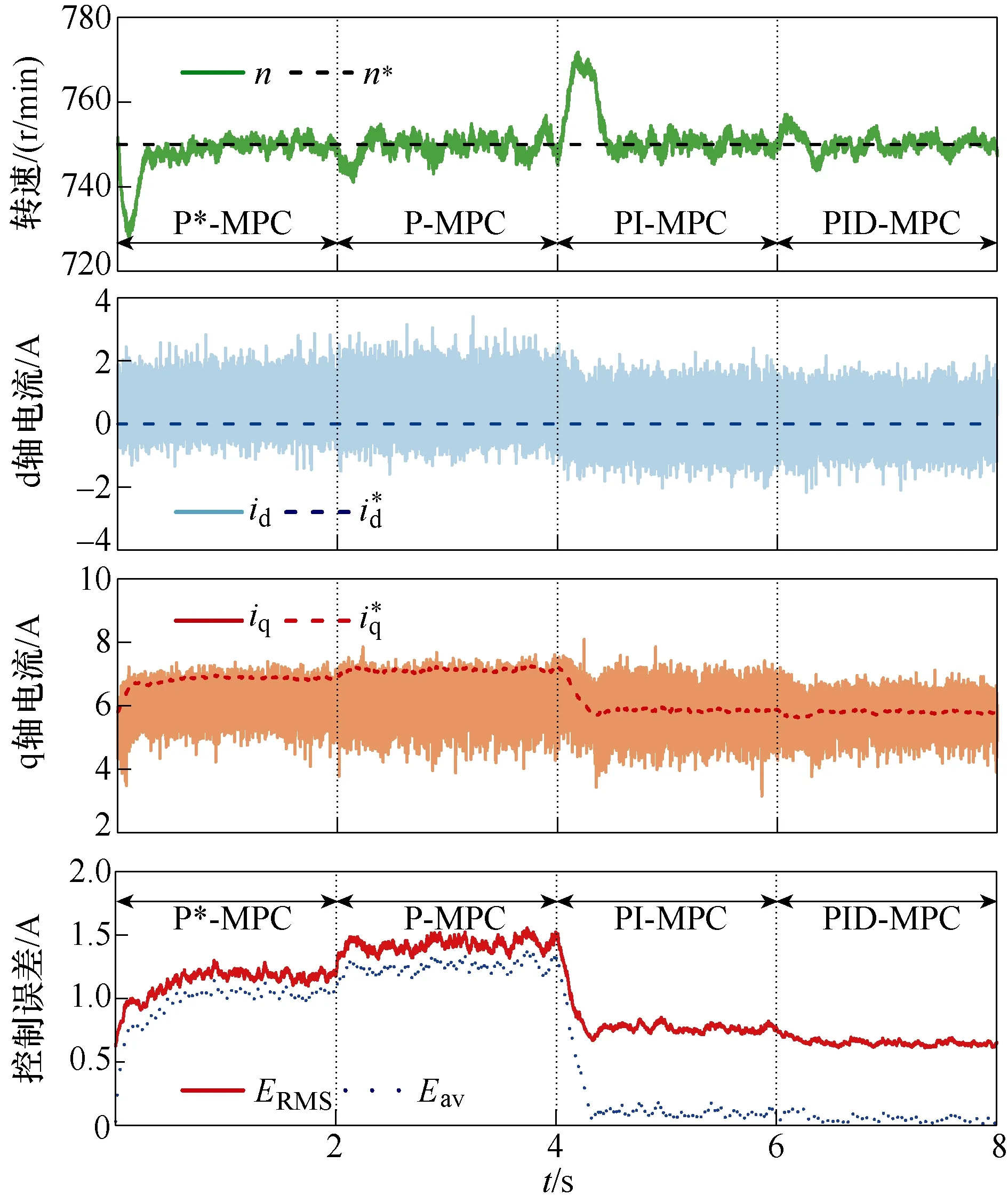
图2 额定转速、转矩下电流控制性能比较Fig.2 Comparison of current control performance under rated speed and load torque

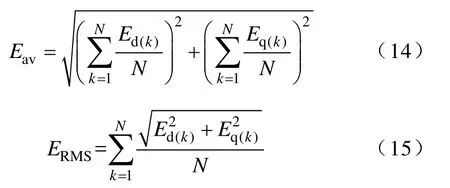
其中

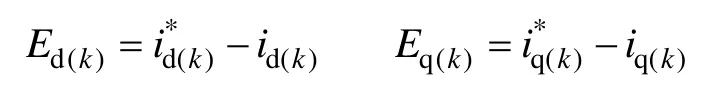
式中，N为采样数。

图3为图2实验中四种方法的相电流波形，总谐波畸变率（Total Harmonic Distortion, THD）计算自 50个连续电周期。从图2、图3中可以看出，P-MPC在模型参数不匹配时，相对于采用额定参数的P*-MPC，电流控制误差与THD均增大。PI-MPC引入积分误差代价后能消除平均误差，但未能降低因模型失配造成的THD升高。而PID-MPC能进一步将方均根控制误差ERMS降低，且THD与P*-MPC接近。此外，P-MPC与P*-MPC均存在平均误差，进而导致相同负载转矩需要更高的相电流，因此效率下降。而PID-MPC则能以相对最小的相电流达到相同的转速和转矩，效率更高。

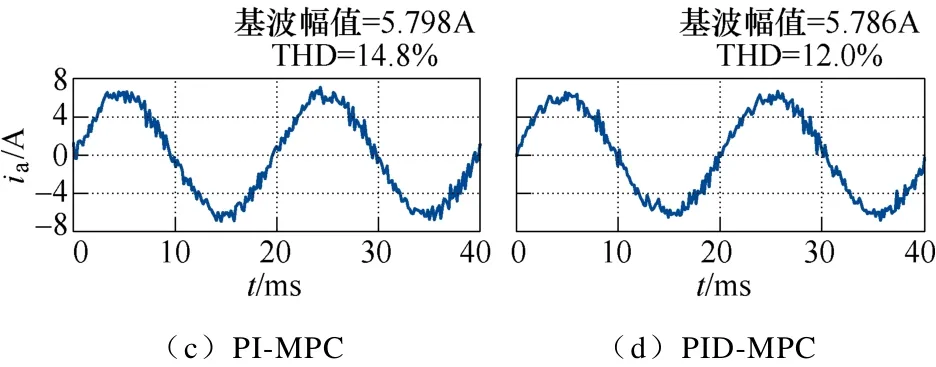
图3 图2中4个实验组的相电流Fig.3 Phase currents of the four groups in Fig.2

值得一提的是，P*-MPC尽管采用了额定参数却未能实现最佳的控制性能，这是由于：一方面，模型未考虑逆变器死区、管压降等非线性因素，因此仍不够精确；另一方面，传统代价函数仅要求下一拍预测误差最小，而未考虑误差的统计规律。

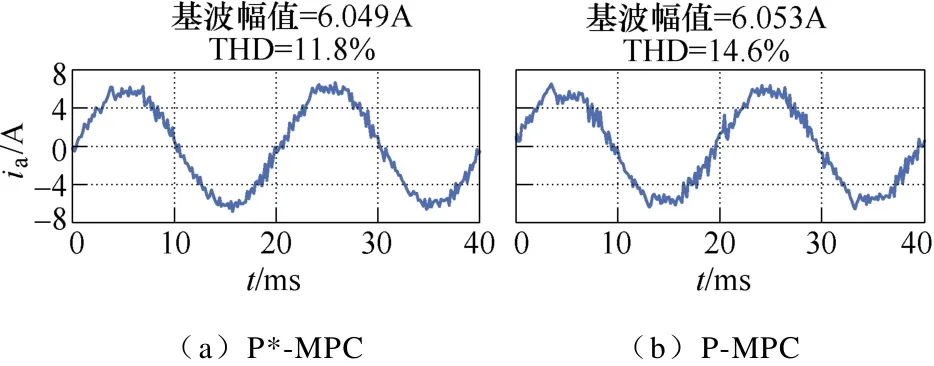
图4为电机运行在375r/min、空载情况下的电流控制性能对比。P-MPC、PI-MPC、PID-MPC的预测模型中电感、电阻、永磁体磁链均为50%额定值，同样每隔2s轮换实验组。可以看出，低速空载的实验结果与额定转速满载时一致：参数不匹配会使电流误差增大；PI-MPC和PID-MPC能基本消除稳态误差，而D的引入使得PID-MPC将ERMS降至最低。

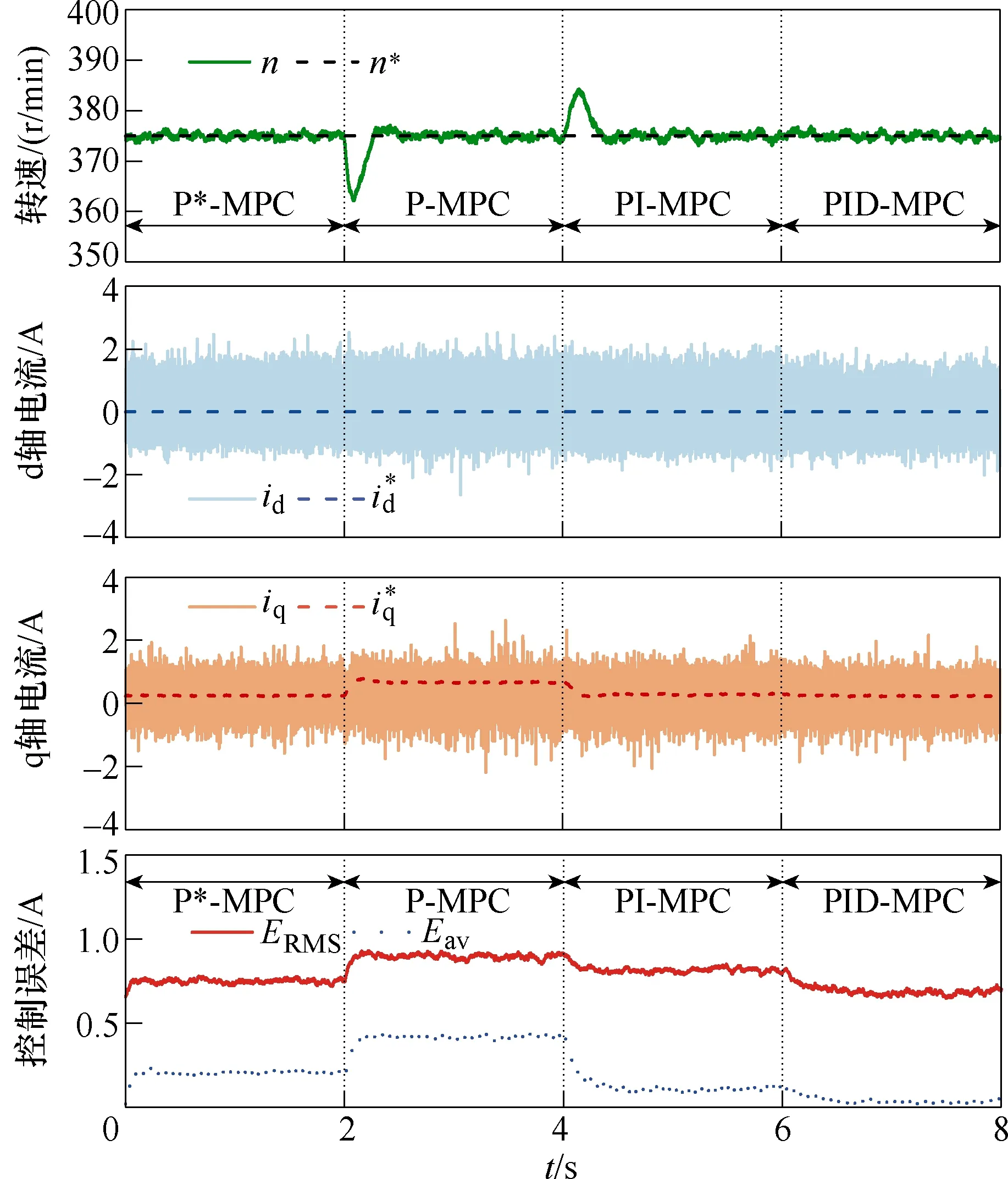
图4 空载50%额定转速下电流控制性能比较Fig.4 Comparison of current control performance under 50% rated speed and no load

图5为预测模型中电感、永磁体磁链、电阻参数分别变化的情况下，P-MPC、PI-MPC和PID-MPC的控制误差比较。数据均在额定转速、额定转矩下测得。图5中带有上标“^”的参数为模型参数，不带上标的为额定参数。图5a～图5c三组实验中，均固定模型电感、永磁体磁链和电阻中的两个参数为额定值，而另一参数从50%变化至200%额定值，以测试单个参数的偏差对于三种方法控制误差的影响。从结果中可以看出，传统P-MPC的电流控制误差对电感和磁链参数敏感，参数不匹配时会使控制误差Eav和ERMS增大，而对电阻参数较不敏感，这与文献[2]结论相符；PI-MPC电流平均误差Eav几乎为零且对参数变化不敏感，但其方均根误差ERMS仍随参数尤其是电感参数的变化而变化，说明 PI型代价函数不能抑制因参数误差而增大的电流纹波；而PID-MPC的电流稳态误差和纹波误差对参数均不敏感，且在相同条件下电流误差最低，说明微分误差代价对纹波误差有改善作用。

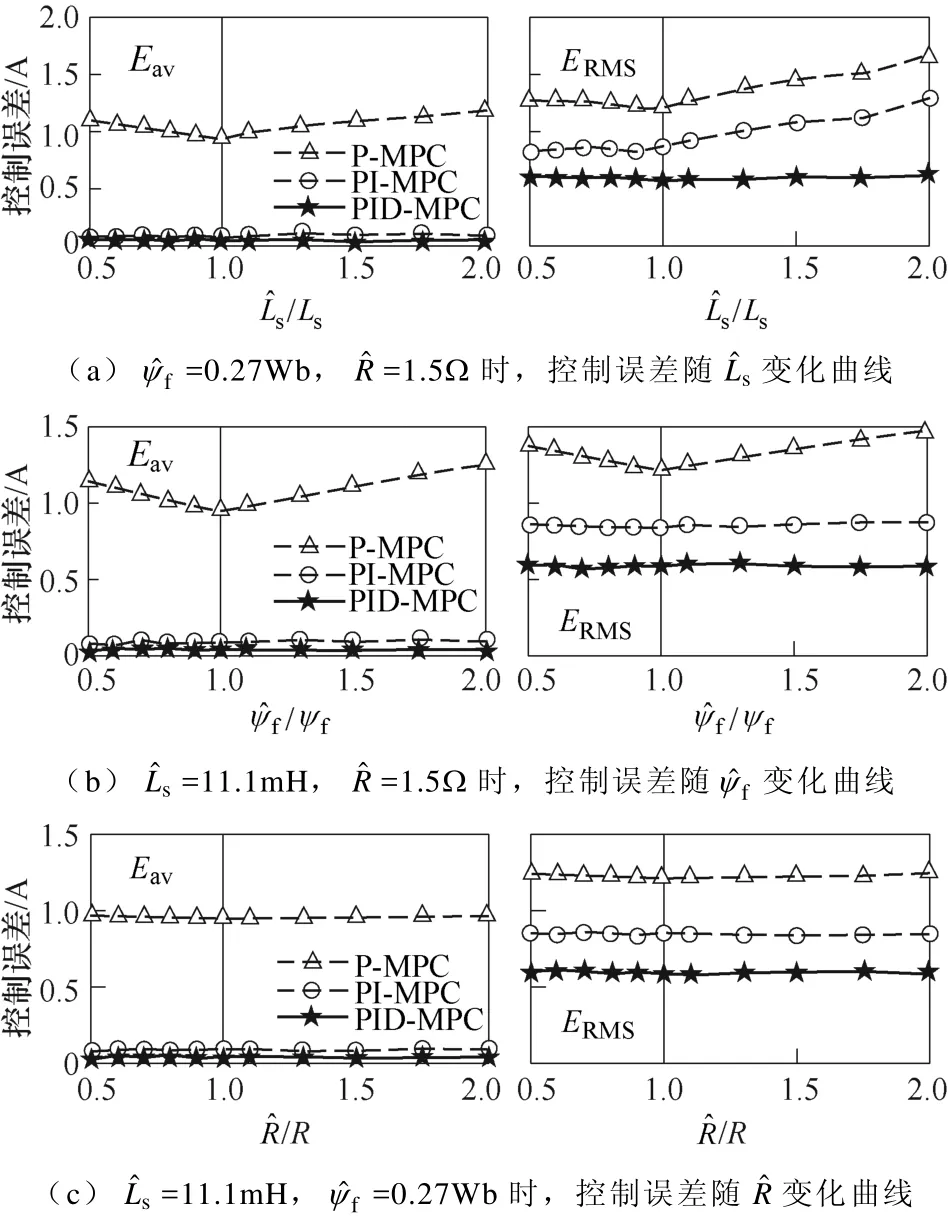
图5 P-MPC、PI-MPC、PID-MPC平均控制误差Eav和方均根控制误差ERMS随模型参数变化曲线Fig.5 Mean control error and RMS control error of P-MPC, PI-MPC and PID-MPC with parameter variations

图6为分别采用PID-MPC和P*-MPC电流控制的PMSM，在第0.2s满载起动至额定转速的实验。其中，PID-MPC采用与P*-MPC一致的模型参数和速度环参数，电流给定值限幅均为8A。可以看出，两种方法在起动瞬间均能实现快速的电流跟踪，说明PID型代价函数不影响FCS-MPC动态响应快的优点。而由于PID-MPC电流控制误差更小，转速达到额定值的时间缩短近33%。

图7为分别采用PID-MPC和P*-MPC电流控制的PMSM在额定状态运行时负载转矩突变的实验。参数设置同图6。可以看出，在转矩变化瞬间，PID-MPC同样能对电流指令快速跟随。从图7还可看出，由于电流控制误差更小，在相同的速度外环作用下，瞬态过程转速变化小于传统的FCS-MPC。

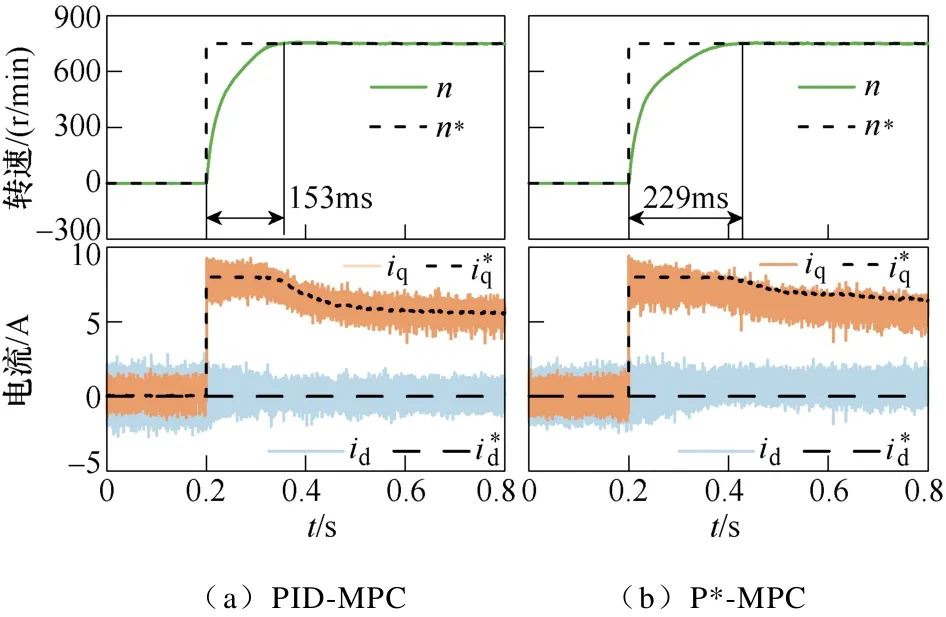
图6 PMSM满载起动实验Fig.6 Experiment of full-loaded startup of PMSM

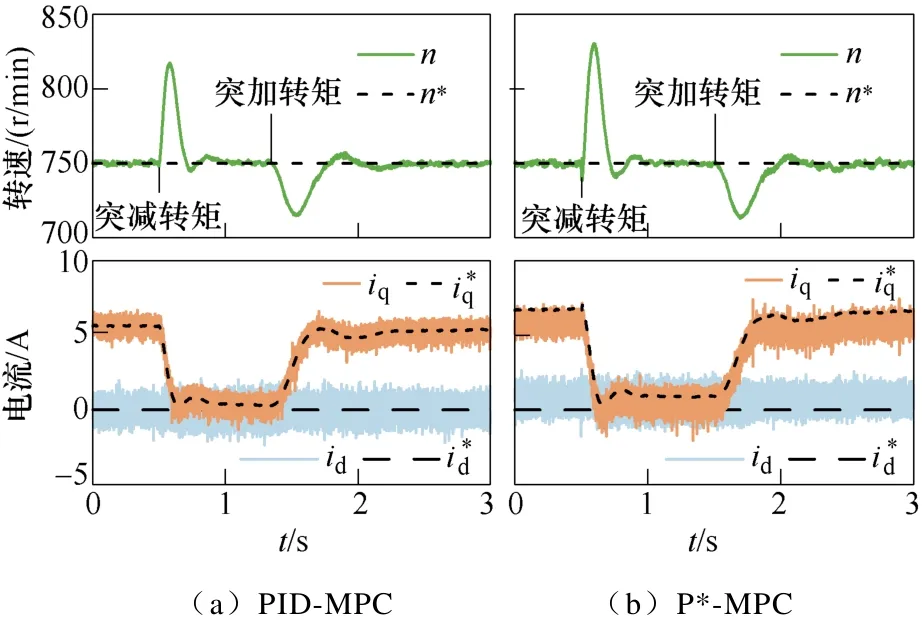
图7 突变额定转矩实验Fig.7 Experiment of step change of rated load torque

4 结论

FCS-MPC电流控制性能对模型参数较敏感，与实际PMSM系统参数不匹配时，会导致电流控制性能下降。对此，本文将 FCS-MPC传统代价函数改进为PID型代价函数，在比例误差代价的基础上，设计了积分误差代价和微分误差代价，在预测模型参数不匹配的情况下，可分别消除稳态电流控制误差和抑制纹波电流。实验结果证明，该方法在参数大范围变化的情况下均能降低稳态误差和纹波误差，提高电流控制性能，并同时保留 FCS-MPC动态响应快的优点。