数字化配电网分布式谐波治理的VDAPF优化配置策略
贾清泉,张雪瑞,刘文邈,张晨瑞,卜令岩
(1.电力电子节能与传动控制河北省重点实验室(燕山大学电气工程学院),河北 秦皇岛 066004;2.国网山西省电力公司大同市云州区供电公司,山西 大同 037300;3.国网辽宁省电力有限公司沈阳供电公司,辽宁 沈阳 110811)
0 引言
随着分布式电源大规模并网和电力电子非线性负荷数量的激增,现代配电网电力电子化程度显著提高[13]。高密度全网分布的谐波源使现代配电网谐波污染呈分散化、全网化态势[4-5],谐波问题愈加严重。
传统配电网谐波源数量较少且分布集中,通常可采用点对点的治理模式从污染源侧就地治理。电压检测型有源电力滤波器(Voltage Detec-tion Active Power Filter,VDAPF)作为点对点治理模式中广泛应用的补偿装置,通过向污染线路注入反向谐波电压形成抵消,以实现谐波治理[69]。文献[10]研究了基于VDAPF的分布式全局优化治理方案,提出一种全局优化与本地控制相结合的分布式治理策略。这些研究工作[11-13]为解决现代配电网谐波问题提供了一种分布式治理的新思路。
分布式电源并网逆变器与VDAPF具有相同的主电路拓扑,因而并网逆变器可以兼有VDAPF的谐波治理功能。采用具备谐波治理功能的多功能并网逆变器(Multi-Functional Grid-Tied Inverter,MFGTI)作为分布式电源的并网接口,在实现有功并网的同时,可利用其剩余容量辅助治理谐波[1419]。文献[14-15]针对谐波、电压偏差、三相不平衡等电能质量问题,研究利用多功能逆变器同时实现谐波、无功、负序补偿的控制策略。文献[16]针对不同分布式电源(Distributed Generation,DG)出力及功率需求情况,分别为多功能逆变器设计相应的控制策略,以确保不同供需状况下的并网和有源滤波功能。
本文考虑MFGTI辅助谐波治理的作用,提出VDAPF配置策略。创建考虑MFGTI安装位置的两阶段分区方法,划分治理区域并确定VDAPF最佳安装节点。计及MFGTI治理资源,建立兼顾经济性和治理效果的多目标VDAPF容量优化配置模型。考虑到谐波及MFGTI剩余容量的不确定性,基于多场景分析技术构建双重不确定性运行场景集。最后,结合规格化法平面约束(Normalized Normal Constraint,NNC)和改进遗传算法求解多目标优化模型。选取IEEE33节点配电系统进行仿真分析,验证了本文所提方法的有效性和经济性。
1 电气设备治理谐波方法
1.1 VDAPF治理谐波方法
治理设备的安装位置、容量不同,对配电网电能质量的治理能力、治理效果也不同。因此,确定合理治理设备分布与容量对治理作用的发挥非常关键。目前已有文献大多是将谐波治理效果最好和以谐波水平达标所需治理容量最小为目标,建立了治理设备优化方案,利用遗传算法、粒子群算法等智能算法进行求解。
利用VDAPF治理谐波,其谐波补偿容量IAPF与等效电导关系如式(1)所示。

式中:GAPF,h,i为接入i节点VDAPF的h次谐波电导值;Uh,i为i节点的h次谐波电压。
1.2 VDAPF联合多功能逆变器治理谐波
考虑电网内配置VDAPF和MFGTI 2种治理设备,其中,MFGTI位于DG安装节点,位置及容量均已知;对于VDAPF,在考虑MFGTI已知的基础上,利用分区算法及优化配置模型得到VDAPF最佳配置信息。VDAPF及MFGTI运行参数由主站端根据采集的谐波电压及DG功率输出信息,从全网角度进行优化求得。
MFGTI与VDAPF基本结构相似,不但具有常规逆变器实现可再生能源并网的基本功能,还增加了谐波治理功能,可利用其实现并网以外的剩余容量进行谐波治理,且补偿原理与VDAPF基本相同。
利用MFGTI剩余容量治理谐波,其谐波补偿容量IMFGTI与等效电导的关系如式(2)所示。

式中:GMFGTI,h,i为MFGTI的h次谐波电导值。
1.3 MFGTI单独治理谐波
当光伏渗透率足够高时,每个点都装有光伏逆变器,若将一些点的普通逆变器换成多功能逆变器,使微电网本身直接具有谐波治理功能。
谐波治理中,MFGTI的最大谐波补偿容量受设备剩余容量限制,需在求得剩余容量的基础上,进一步计算得出。对于MFGTI可参与谐波治理的设备剩余容量Sre,仅考虑DG并网有功功率PDG,则Sre与总容量SN及PDG的关系为

式中:SN为定值,故MFGTI剩余容量主要由PDG决定。PDG受天气影响,具有不确定性,致使MFGTI参与谐波治理的剩余容量同样具有不确定性,且与天气情况紧密相关。由剩余容量Sre即可确定MFGTI用于谐波治理的最大可补偿容量

式中:UN,i为节点i的额定基波电压。
2 VDAPF和MFGTI协同谐波治理分区及设备安装节点确定方法
2.1 VDAPF和MFGTI协同治理分区方法
谐波治理分区应满足区域内节点强耦合、区域间节点弱耦合的特点,且各区治理设备的安装节点,应具有较强的控制能力。按谐波治理设备初始配置情况,配电网节点可分为普通节点和配有MFGTI的DG节点。考虑到DG节点已具备一定谐波治理能力,为满足上述分区的要求,分两阶段进行谐波治理分区,具体分区方法如下。
2.1.1 第1阶段分区
设网络含a个DG节点,以每个DG节点为中心,根据DG节点对不同节点的控制效果,形成a个初始DG治理区域。
a.求节点谐波响应灵敏度。节点谐波电压与节点注入谐波电流满足关系式(5),由此计算h次节点j谐波电压对节点i注入谐波电流的灵敏度wI,h,ji,进而得到节点总谐波响应灵敏度wI,ji,具体见式(6)、式(7)。

式中:Yh为节点导纳矩阵,取其某一负荷场景下的典型值用于计算;A为Yh的伴随矩阵;Uh,j为节点j的h次谐波电压;Ih,i为节点i的h次谐波补偿电流;Ai,j为矩阵A中元素;N为谐波频率总个数。
b.将普通节点对各DG节点的谐波响应灵敏度从高到低排序,设定阈值ϑ,选出谐波响应灵敏度高于ϑ的节点,并划分到与其响应灵敏度最大的DG节点的控制区域。
c.求节点谐波耦合度。按式(8)计算区内h次任意的节点i对节点j谐波电压的响应灵敏度wU,h,ij,进而按式(9)得到节点总谐波耦合度βij。

d.为保证区内节点高耦合的要求,设置耦合度最低限值ξ,将区内各节点间谐波电压耦合度不满足要求的节点作为待定节点。
e.针对不满足耦合度要求的各组待定节点,若其中一个节点为DG节点,则直接剔除另一节点;若不含DG节点,则计算2节点与区域内其他节点间的谐波耦合度,剔除耦合度之和较低的节点,以确保区内节点的强耦合性。最终所得各初始DG治理区域的节点满足式(10)的要求。

式中:z为区域内DG节点。
2.1.2 第2阶段分区
在第1阶段分区基础上,基于社团发现算法,求得全网最优分区结果。
本阶段将每个未分区节点和初始DG治理区域均视为独立的社团,作为网络初始分区,在此基础上应用社团发现算法划分网络,并以最大模块度对应分区作为最终分区结果。网络划分以谐波电压耦合度作为节点关联程度的评判指标,且连边权重Aij∈[0,1],因此,设定节点i与j的连边权重Aij如式(11)。

2.2 VDAPF最佳安装节点的确定
含DG节点的区域虽具备一定的谐波治理能力,但通常不足以使区内各节点谐波水平均达标。因此,需对所有区域配置VDAPF。
VDAPF的最佳安装节点应对区内各节点具有较强的可控性。利用最大平均灵敏度节点作为VDAPF安装节点,平均灵敏度的计算见式(12)。

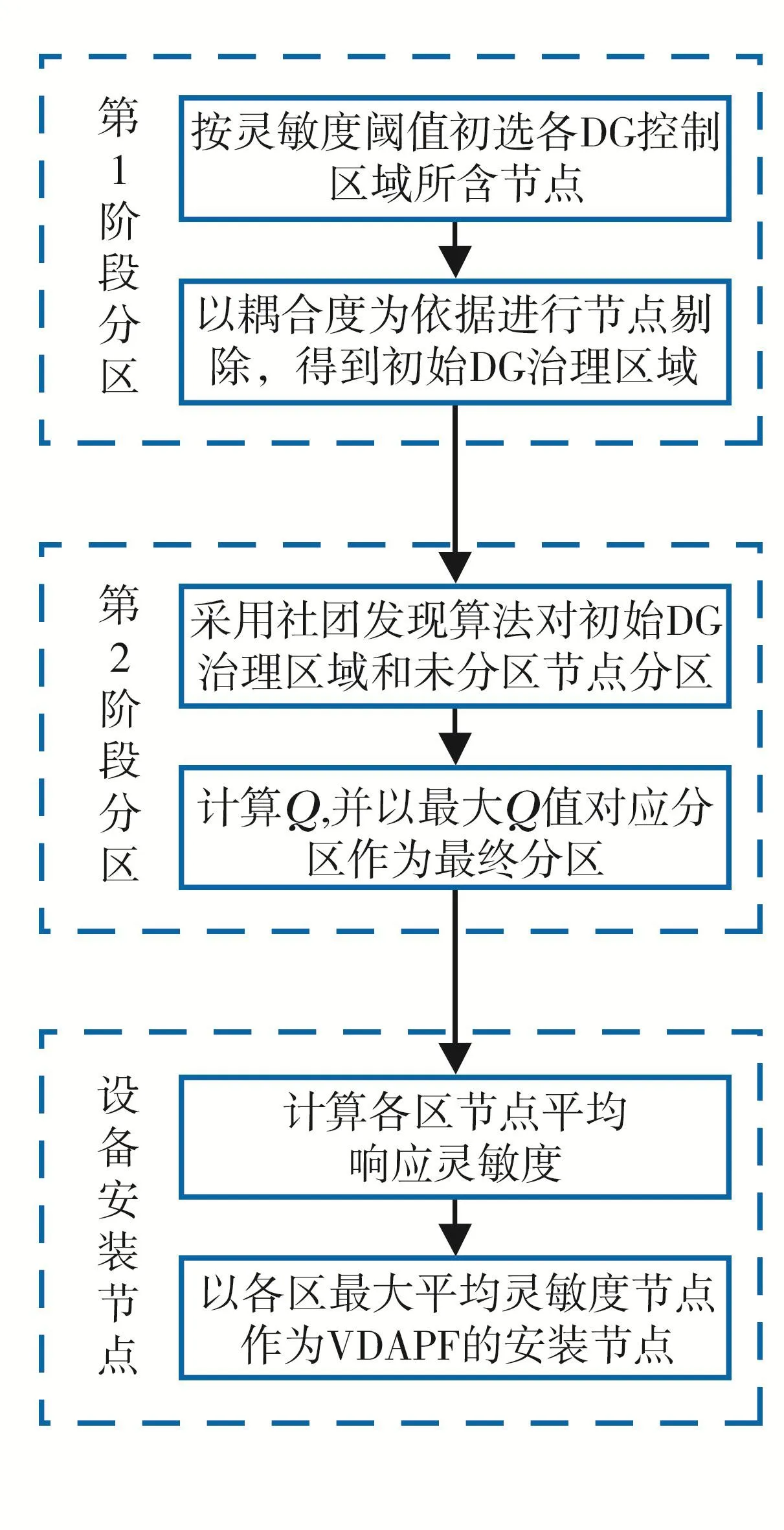
图1 谐波治理分区及VDAPF安装节点确定流程
2.3 双重不确定性场景的构建
本文以规划年为时间域,将全年按季节划分为不同的典型日,再按时序对典型日划分时段,以小时级时间尺度对典型日进行时段划分。划分时段后,对其中某一时段t构建运行场景,具体方法如下。
a.针对谐波不确定性,以t时段内网络n个节点的谐波预测信息构建该时段的谐波场景,一组网络谐波信息作为一个场景,用向量H表示,由若干谐波向量构成原始谐波场景集M。

式中:H i为节点i在时段t内的谐波电流;N+为非零自然数集合;H'v为第v个原始谐波场景;m为原始谐波场景的数量。
由于原始谐波场景数量过多,采用k均值聚类法进行场景压缩[20],聚合出具有代表性的典型谐波场景集C,其中第γ个典型场景发生的概率为P(Hγ)。
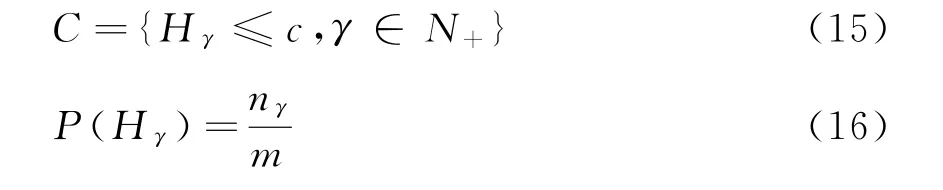
式中:Hγ为第γ个典型谐波场景;c为典型谐波场景的数量;nγ为Hγ这一类包含的原始场景数量。
b.针对MFGTI剩余容量的不确定性,对各时段按MFGTI剩余容量大小分为不同场景,构成MFGTI剩余容量场景集G。

式中:G a为第a个逆变器剩余容量场景;g为逆变器剩余容量场景的数量。
基于概率密度拟合法,可得光伏并网有功功率P PV的概率密度函数,用f r(r)表示[23]。利用f r(r)可求得处于第a个场景G a发生的概率P(G a)及均值μa。
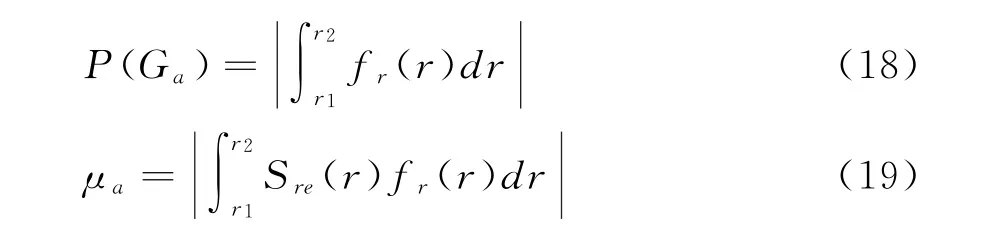
式中:r1和r2分别为G a的剩余容量下限S re,a1和上限S re,a2所对应的光照强度。
c.谐波治理运行场景Y兼顾谐波及MFGTI剩余容量的不确定性,故Y由典型谐波场景C和MFGTI剩余容量场景G共同构成。所得双重不确定场景集Y、场景个数及场景概率见式(20)-(22)。

式中:Y l为时段t内第l个规划场景;R(g)表示集合中元素的数量;P(Y l)为Y l发生的概率。
2.4 VDAPF容量最优化配置
本文VDAPF安装容量的优化,在考虑经济性的基础上,兼顾谐波治理效果,以VDAPF投资成本最小为目标函数1,以多运行场景下VDAPF和MFGTI协同治理的谐波电压畸变率加权之和最小为目标函数2。运行场景采用2.3节构建的考虑谐波污染及MFGTI治理功能双重不确定性的场景集。基于上述思路构建VDAPF优化配置模型,基本结构如图2所示。

图2 VDAP优化配置模型基本结构
2.4.1 目标函数
2.4.1.1 目标函数1
关注谐波治理经济性,考虑设备购置成本和安装成本。

式中:n为网络节点总数;d i为是否安装VDAPF,若安装用1表示,若不安装用0表示;C i为第i个节点VDAPF的安装费用;k为VDAPF单位容量费用;I*APF,i为第i个节点VDAPF的安装容量。
2.4.1.2 目标函数2
各场景下的电网谐波电压畸变率之和评估治理效果,以总畸变率最小为目标函数。

式中:P y为场景y发生的概率;T HD y为场景y下所有节点谐波电压总畸变率。式(25)为T HD y目标函数。

式中:为场景y下节点i的h次谐波电压,可由h次谐波潮流计算求得。
2.4.2 约束条件
2.4.2.1 谐波潮流方程等式约束

2.4.2.2 VDAPF和MFGTI可选谐波补偿容量约束为保障VDAPF和MFGTI安全运行,所有场景下VDAPF和MFGTI参与谐波补偿容量在不超过其安装容量基础上,需留有一定的容量裕度。
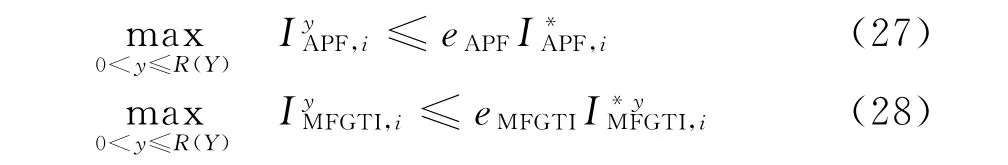
2.4.2.3 节点总谐波电压畸变率约束
治理后配电网每个节点的总谐波电压畸变率要求符合GB/T 14549-1993《电能质量 公用电网谐波》的规定[24]。
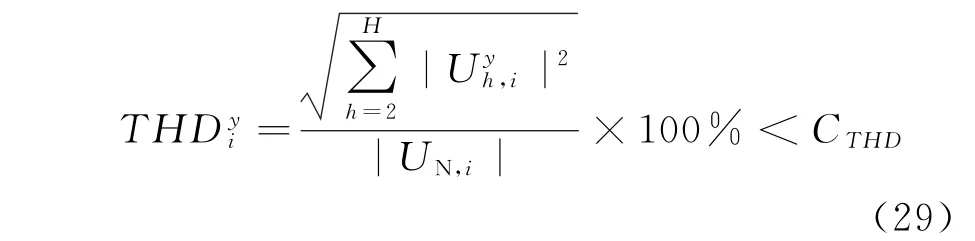
式中:C TH D为节点总谐波电压畸变率最大值。
2.4.2.4 VDAPF安装容量约束
VDAPF安装容量为有上限的离散变量。
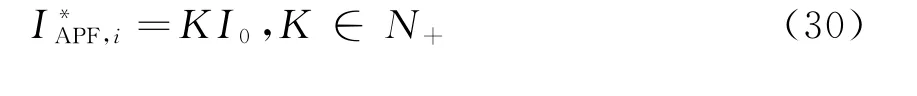

式中:I0为VDAPF的单位最小可安装容量;为VDAPF节点最大可安装容量。
3 算例分析
3.1 算例说明
选取IEEE 33节点配电系统模型进行仿真验证,网络结构如图3所示。根据本文研究需要,在低压侧各节点设置谐波源,以表征高密度的分散谐波,节点6、24和27为分布式光伏并网节点,相应的MFGTI配置信息如表1所示。线路及VDAPF相关参数设置均参考文献[14],MFGTI及VDAPF的容量裕度安全系数均设为95%。按GB/T 14549-1993规定,设置谐波电压畸变率的允许上限为4%。谐波响应灵敏度阈值取最大灵敏度的70%,设置初始DG治理区域内节点耦合度最低限值。光照和谐波数据参照河北某地区的年平均光照和谐波的调研数据,并按本文网络结构做出相应调整。
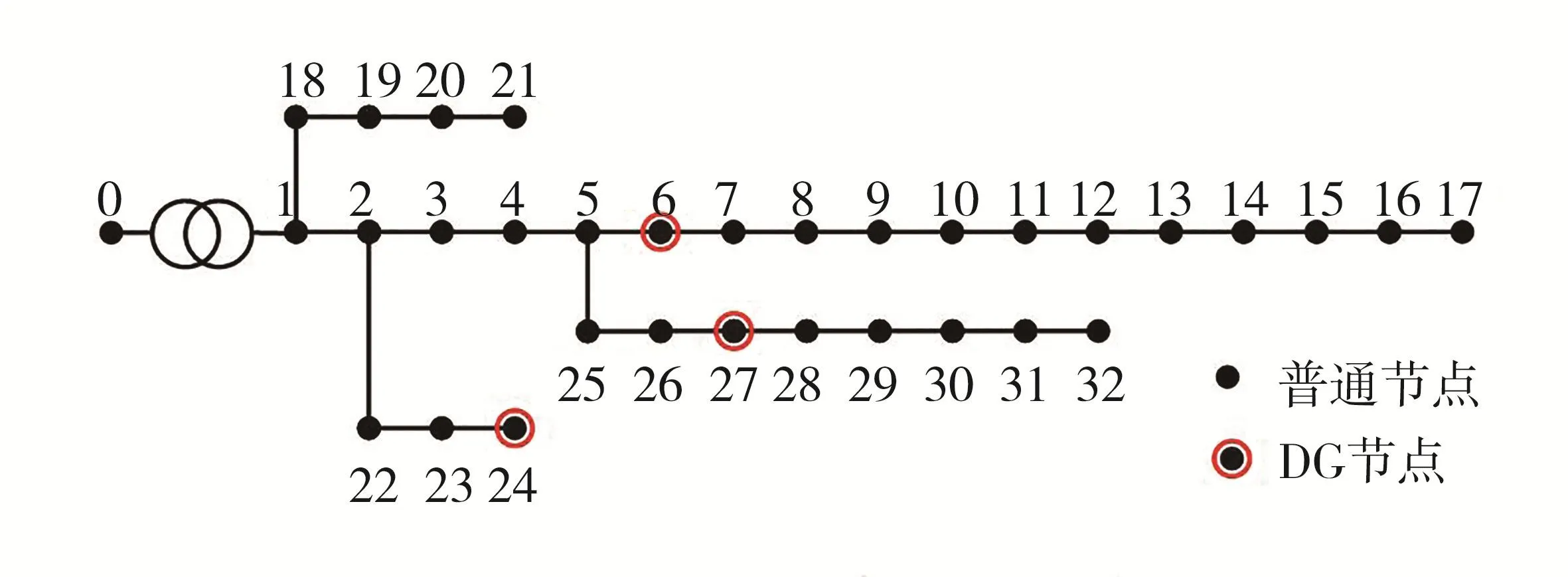
图3 IEEE33节点配网结构

表1 MFGTI配置信息
为简化计算,首先进行时段划分,将全年分为4个典型日,每个典型日划分为24个时段,然后,分别对这96个时段进行场景构建。对96个不同时段的谐波调研数据,以1组32节点各次谐波含量数据为1个原始谐波场景,将同一典型日同时段的原始谐波场景进行聚类,96个时段均各自得到4个典型谐波场景。对96个不同时段的光照强度分别进行概率密度函数拟合,因夜间光强始终为零,夜间各时段均仅有1个MFGTI剩余容量场景;将日间按光强大小分为低、中、高3个等级,则日间各时段MFGTI剩余容量场景数为3。将同时段的典型谐波场景和MFGTI剩余容量场景按2.3节方法组合,即可得该时段的运行场景集。
限于篇幅,本文仅以谐波含量最大的场景为例。在所有谐波场景中,最大谐波场景处于第2个典型日12:00-13:00时段。该时段为日间中午时段,光照充足,逆变器剩余容量较少,按光强高、中、低划分为3个场景,根据式(3)、(18)、(19)计算不同光强等级下各节点的MFGTI剩余容量均值及对应发生概率,构建逆变器剩余容量场景,结果如表2所示。

表2 MFGTI剩余容量均值及概率
3.2 谐波治理区域划分结果
考虑5、7、11、13次谐波,采用2.1节2阶段分区方法进行谐波治理分区。按第1阶段分区方法,以DG节点为中心,对网络节点进行筛选和剔除,得到初始DG治理区域,具体如表3所示。

表3 初始DG治理分区结果
在表3划分结果的基础上,按第2阶段分区方法,采用社区发现算法划分区域,得到模块度函数Q与区域数关系如图4所示。

图4 Q值与分区个数关系
由图4可知,区域数为5时Q值最大,最大值为0.589,则最佳分区数为5,将对应划分结果作为最终分区,并按灵敏度最大准则确定VDAPF安装节点,具体分区及配置结果如图5所示。

图5 配电网区域划分结果
3.3 VDAPF配置结果及谐波治理分析
利用NNC法结合改进遗传算法求解此模型,得到16个帕累托前沿点,如图6所示,每个帕累托前沿点代表了1种规划方案。

图6 16个帕累托前沿点数据
由图6可知,谐波治理经济成本随总谐波电压畸变率降低而增加,说明治理水平的提高势必以经济性为代价。综合上述分析,按照经济投资与治理效果的高回报率原则,以及谐波治理水平不应过低的规避风险原则,选取图中所标记前沿点作为折中解,具体配置方案信息如表4所示。实际应用中,也可按照具体配电网对谐波治理效果的要求及决策者意向,选择所需最优配置方案。

表4 所选配置方案信息
按表5方案配置VDAPF,利用VDAPF和MFGTI协同进行谐波治理,得到了谐波治理前后全部784个运行场景下各节点电压畸变率如图7所示。

图7 治理前后各节点谐波电压畸变率
由图7可知,治理后所有场景下各节点谐波污染状况明显改善,达到国家标准。治理前,各节点电压畸变率均超过国标规定值4%,整体处于8.8%左右。利用VDAPF和MFGTI协同治理后,所有节点谐波电压畸变率明显下降,均降至规定的4%以下,整体保持在2.8%左右。说明考虑MFGTI辅助治理的VDAPF分布式配置策略,可有效进行谐波治理并达到规定标准,验证了本文策略的有效性。
4 结论
为充分利用谐波治理资源,本文提出了一种计及MFGTI贡献VDAPF分布式谐波治理优化配置策略,并以IEEE 33节点配电网络进行仿真分析,说明本文方案可充分利用治理资源,显著提高系统经济性。本文主要研究三相谐波平衡条件下VDAPF配置问题,对于不平衡情况,可按最大一相所需治理容量配置。治理中VDAPF的不平衡输出,易导致直流电压波动增大,如何有效控制VDAPF输出仍有待研究。本文主要贡献及结论如下。
a.提出考虑MFGTI谐波治理功能的两阶段分区方法和VDAPF容量优化模型,确定了合理的网络分区和VDAPF最佳配置方案。仿真结果表明本文方案可提高逆变器的设备利用率,有效减少VDAPF的安装容量,实现更为经济合理的配置。
b.构建兼顾经济性和治理效果的双目标优化配置模型,并求解出多种治理水平的配置方案,为不同决策需求提供了选择性。
c.基于多场景分析技术构建计及MFGTI剩余容量和谐波不确定性的运行场景集,考虑了复杂不确定性对规划造成的影响,同时压缩了运行场景数,减少了计算量。

