翼间干涉效应对蜻蜓悬停气动性能的影响

彭连松，郑孟宗，潘天宇，苏冠廷，李秋实

北京航空航天大学 能源与动力工程学院，北京 100083

大多数昆虫在进化过程中逐渐退化为一对翅膀飞行(如双翅目昆虫)或者前后翅只能同相位飞行(如膜翅目昆虫)[1]。蜻蜓作为极少数可以独立控制两对翅膀运动的昆虫，可以通过调节翅膀的运动规律，利用两对翅膀之间的干涉效应拥有出色的飞行能力。蜻蜓能够进行快速前飞(最高54 km/h)、悬停、倒飞和滑翔，可以在3个拍动周期内完成180°转弯[1-5]。此外蜻蜓是目前发现唯一可以进行跨大洋迁徙的昆虫[6]。蜻蜓的高机动性和持久飞行能力是微型飞行器(Micro Aerial Vehicle, MAV)追求的特性。因此研究人员希望通过研究蜻蜓为MAV的设计提供帮助[7-8]。

在众多飞行状态中，悬停是蜻蜓观察猎物、调整飞行状态的重要行为，也是MAV进行观测等工作时不可缺少的状态[9]。因此为了研究蜻蜓悬停飞行的气动机理，研究者们对蜻蜓悬停进行数值计算和模型试验。Sun和Lan[10]对蜻蜓扑翼进行三维数值模拟，指出与单翅拍动相比，干涉效应使前翅和后翅的升力分别减小14%和16%。Lu等[11]通过在水洞中进行模型试验，认为在大多数相位差下，干涉对前缘涡有害，程度随前后翅的距离增加而减弱，导致形成的前缘涡小于单翅。Zheng等[12]通过对串列翅膀的悬停扑翼进行气动力和粒子图像测速(PIV)测试，认为在0°相位差下，双翅扑翼产生的气动力大于单翅，90°相位差下，双翅产生的平均气动力与单翅大致相同，180°相位差下，双翅产生的平均气动力小于单翅。

上述针对蜻蜓悬停的研究表明，在悬停状态下，翼间干涉不利于升力的产生。但是悬停作为一种准静态的飞行状态，飞行速度为零，所受合外力为零，只需产生与自身重力相等的气动升力即可，因此与前飞、爬升、转弯等机动飞行相比对气动力的要求不高。但与前飞和爬升等运动状态相比，由于无法利用前飞速度获得伯努利效应和其他非定常高升力机制，维持悬停状态需要更大的气动功率[13]。针对蜻蜓悬停状态的研究应聚焦在翼间干涉对于效率和功率的影响,但大多数相关研究重点关注翼间干涉对气动力的影响，缺乏对于悬停效率和功率的影响研究。仿生学在航空领域得到广泛应用[14-15]，蜻蜓独特的双翅扑翼是否会提升悬停效率，产生高效率的扑翼机制，进而为MAV设计提供灵感，是值得研究的问题。

本文通过数值仿真方法，模拟蜻蜓在悬停状态下的串列双翅扑翼和单对翅扑翼，通过对两种模式的气动特性和流场结构进行对比分析，得到翼间干涉影响悬停效率和功率的效应。

1 模型与方法

1.1 翅膀模型及运动规律

如图1(a)和图1(b)所示，翅膀的位置由基于拍动平面的3个欧拉角确定：拍动角φ、翻转角θ和偏移角ψ。其中φ为Z轴与翅根翅尖连线在拍动平面上的投影所成夹角，θ为翅膀的弦线与其在拍动平面的投影所成夹角，ψ为翅根翅尖连线与其在拍动平面上的投影所成夹角。攻角α与θ的关系为：翅膀下拍过程中α=θ;上拍过程中α=180°-θ。

Norberg使用高速摄像机对悬停状态下的蜻蜓进行拍摄，并对所拍摄蜻蜓进行生物学测量[16-17]。通过对拍摄的图片进行分析，发现蜻蜓在悬停时身体与水平面平行，翅膀的扑动频率f=36 Hz，翅膀的拍动平面与水平面夹角β为60°，前翅扑动角的变化范围为水平面以上+35°到水平面以下-25°，后翅扑动角的变化范围为+45°～-15°，后翅拍动领先前翅的相位差γ为180°。被观测蜻蜓的平均重量为754 mg，前翅展长为4.74 cm，平均弦长为0.81 cm，后翅展长为4.60 cm，平均展长为1.10 cm[17]。本文采用上述翅膀运动规律和几何形状(如图1(c)和图1(d)所示)，其中翅膀厚度设置为平均弦长c的0.01倍。

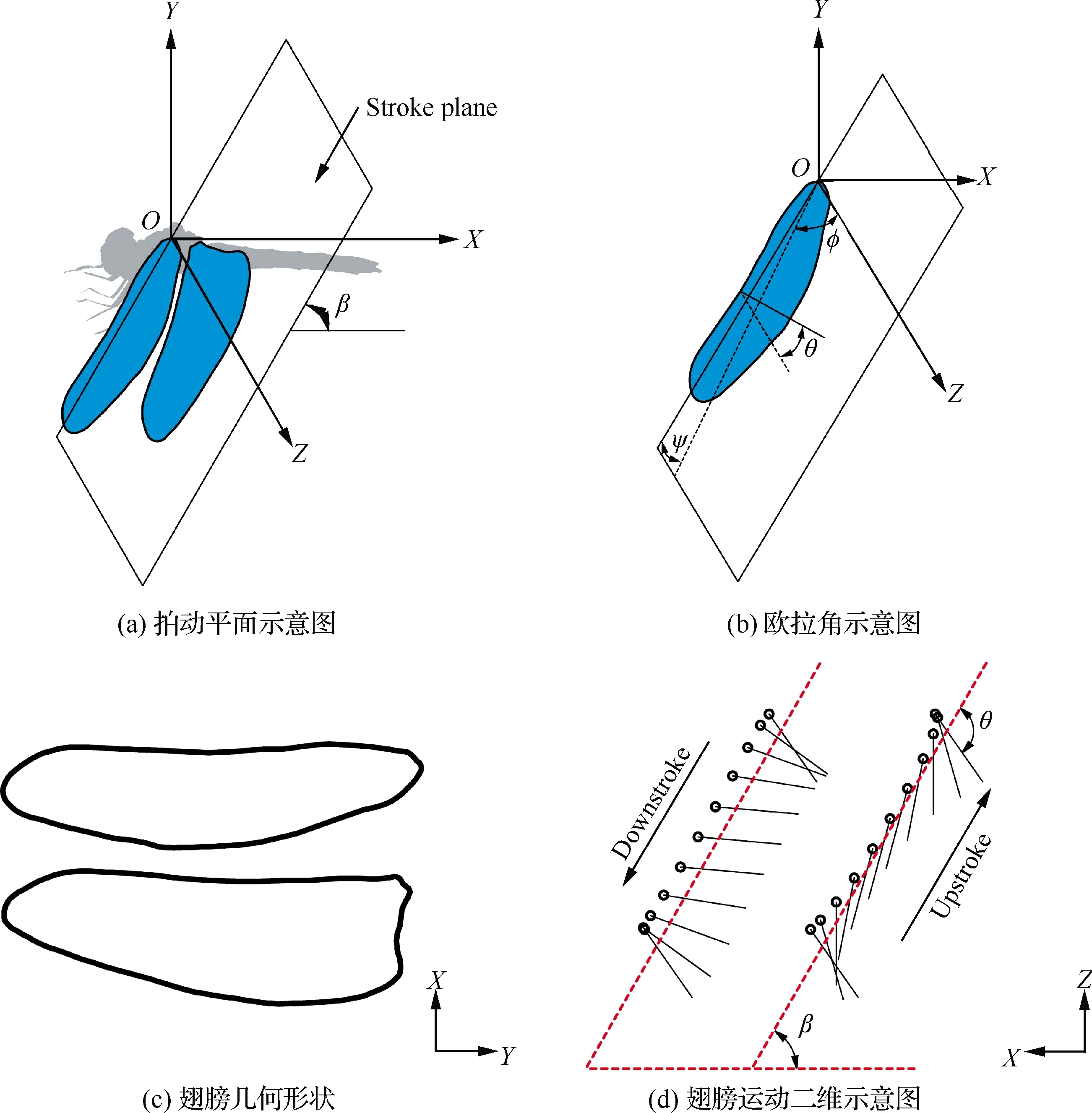
图1 蜻蜓翅膀模型的参数定义

Norberg在进行观测时只使用了一台摄像机，无法获取翅膀的空间三维参数，所以无法得到翻转角θ的信息。由于使用的摄像机频率较低(80 Hz)，无法得到拍动角等参数随时间变化的准确规律。因此为了获取蜻蜓悬停状态下翅膀运动的准确运动规律，需要参考他人的研究和测量结果。由Azuma[4,18]、Wakeling[19]、Wang[20]和Ellington[21]等的观测结果可知，蜻蜓飞行过程中拍动角的变化规律可以用一阶傅里叶变换准确描述，即拍动角可以表示为时间t的三角函数形式；翻转角在上拍和下拍过程中近似不变，而在一次拍动结束到下一次拍动开始的一段时间内近似正弦变化。因此将Norberg[16]的数据进行插值可得到前翅拍动角φf和后翅拍动角φh的变化规律:

φf=5°+30°cos(226.08t)

(1)

φh=15°+30°cos(226.08t+3.14)

(2)

根据Azuma[18]和Wang[20]等的测量数据，翻转角的变化规律θ(t)为

(3)

式中：无量纲翻转时间ΔT=0.4;上拍翻转角θu=170°;下拍翻转角θd=65°,前翅和后翅翻转角变化规律相同。由于偏移角ψ呈现无规律变化，且数值接近0°，因此忽略偏移角的影响，将其设置为0°。

双翅在拍动周期内的完整变化规律如图2所示，规定周期T=0时，前翅位于下拍起始点，后翅位于上拍起始点。灰色区域代表前翅的上拍区域和后翅的下拍区域。

图2 双翅运动规律

翅膀的二次矩半径r2定义为

(4)

式中：r为径向距离；S为翅膀表面积。

特征速度Uref定义为r2处的平均拍动速度：

Uref=2φr2f

(5)

式中：φ为拍动角幅度；f为拍动频率。

拍动过程中雷诺数Re定义为

(6)

式中：ν为空气的运动黏性系数。前翅和后翅的雷诺数分别为1 196和1 572，与Li[5]和Wakeling[19]等的观测结果相近。

1.2 数值模拟方法

在商用数值软件Xflow 2019环境下通过格子-玻尔兹曼方法(Lattice Boltzmann Method，LBM)进行模拟。与基于离散化的宏观Navier-Stokes(N-S)方程的传统数值方法不同，LBM方法采用介观模型，将空间离散为笛卡尔分布的格点(Lattice)，每个格点上沿不同方向的速度为ei(i=1,2,…,b)。连续空间中Boltzmann输运方程为

(7)

式中：fi(R,t)表示在t时间速度为ei的粒子在位置R处的分布;Ωi为碰撞算子，计算质量守恒和动量守恒下的碰撞。LBM方法在介观尺度通过求解格子-玻尔兹曼方程模拟粒子间的碰撞和迁移，通过平衡态分布函数将介观尺度下粒子的碰撞和迁移回归到宏观尺度的物理场。

LBM方法将求解域划分为笛卡尔直角坐标系下的有限个格子，使得求解过程中网格划分过程被极度简化，同时可以更快更准地求解复杂表面的动边界问题。如图3所示，翅膀表面为无滑移壁面(Non-slip Wall)，进出和出口为压力边界条件。为了节约计算时间，仅对左侧的前翅和后翅进行模拟，通过在侧面设置对称边界条件模拟右侧翅膀的影响。

图3 计算域及边界条件

1.3 算例验证

为了验证软件模拟扑翼运动的能力，使用Xflow对二维蜻蜓扑翼[22]和三维果蝇扑翼[23-24]进行模拟和试验。其中二维算例计算域为20c×20c，每周期计算1 000步。三维算例计算域为15c×15c×10c，每周期计算500步。对每个算例进行了计算域、时间步和网格尺寸的无关性验证，确保进一步改进平均升力的变化不大于0.5%。计算结果与已发表结果的对比如图4所示,由对比结果可以看出，LBM方法的模拟结果与前人的试验和数值结果绝大多数吻合得很好。产生差异的原因可能在于所采用翅膀的几何形状略有不同。

图4 数值方法验证结果

在对蜻蜓悬停进行进一步仿真之前，参考对于Xflow在非定常仿真中收敛性和精度的研究[25]，本文对仿真所用的格子尺寸和时间步进行调整，以满足无关性。最终确定格子尺寸为0.02c，计算域15c×15c×10c,每周期计算600步，确保格子尺寸、计算域和时间步再细化，气动力变化在0.5%以内。

2 数值结果与分析

2.1 蜻蜓悬停状态气动性能

翅膀在空气中从静止开始拍动，直到力系数出现良好周期性后认为达到稳定状态。图5所示为T=0.8时刻翅膀周围的三维涡量图。前后翅的总阻力系数和总升力系数随时间变化如图6(a)所示，可以看出第5个周期开始周期性良好，故选取第5、6周期的数据进行受力和流场分析。

图5 T=0.8时刻三维涡量图

计算得到的平均阻力为0.14 mN，近似为零，平均升力为7.68 mN，可以提供768 mg的升力，与重力(754 mg)大概相等，因此可以认为采用本文的运动规律进行扑翼运动可以达到悬停状态。周期平均后的阻力近似为零，对气动效率和功率的影响较小，故气动力的分析以升力为主。为了使结果更具普适性，本文将气动力F转化为力系数CF进行分析，两者关系为

(8)

图6(b)和图6(c)分别为单翅/双翅拍动的前翅和后翅升力系数在一个周期内的变化曲线。可以看出翼间干涉对前翅影响较小，对后翅影响较大。单翅拍动和双翅拍动下前翅产生的平均升力系数分别为1.26和1.15，单翅拍动和双翅拍动下后翅的平均升力系数为1.22和0.98，双翅干涉使前翅和后翅平均升力系数分别减小了8.7%和19.7%；翼间干涉在翅膀下拍行程中双翅距离较近时影响效果明显，前翅在T=0.2～0.4时、后翅在T=0.7～0.9时升力下降明显。

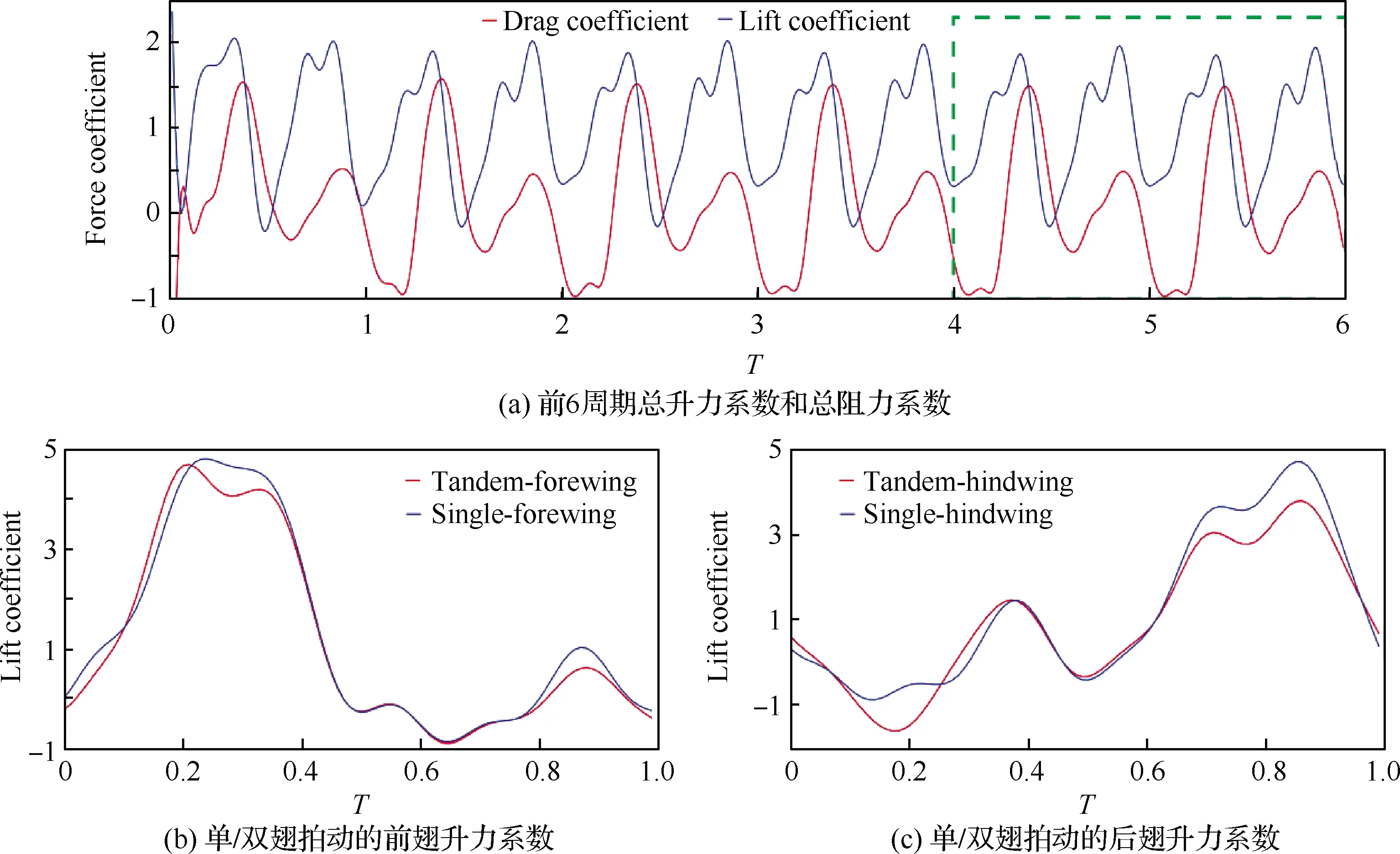
图6 单翅/双翅拍动力系数

翅膀在扑动过程中克服气动力所需功率可以通过计算力矩和角速度的乘积得到。单翅拍动和双翅拍动下前翅平均功率分别为8.4 mW和8.0 mW，后翅平均功率分别为10.0 mW和8.6 mW。前翅和后翅的气动功率分别下降了4.8%和14.0%。

本文对蜻蜓悬停效率的定义为维持悬停状态所需的理想功率与翅膀运动实际所需的平均气动功率的比值。由于悬停中的蜻蜓与直升机相似，因此参考直升机悬停效率的计算公式，翅膀视为激盘模型，运用动量定理和质量守恒定理得到悬停效率公式为

(9)

式中：L为翅膀产生的总升力；Pa为翅膀运动克服的气动功率；A为翅膀扫过的面积。由于双翅拍动模型中前翅和后翅视为一个激盘模型，因此得到的双翅悬停效率为前翅和后翅共同作用的结果。单独拍动的前翅和后翅的悬停效率分别为22.91%和21.65%，双翅拍动的悬停效率为27.18%。对比单独拍动的前翅和后翅，翼间干涉使悬停效率分别提高了18.6%和25.5%。

翼间干涉效应对前后翅气动参数的影响总结为表1。翼间干涉对前翅影响较小，对后翅影响较大，使翅膀的平均升力和气动功率减小，使悬停效率增加。

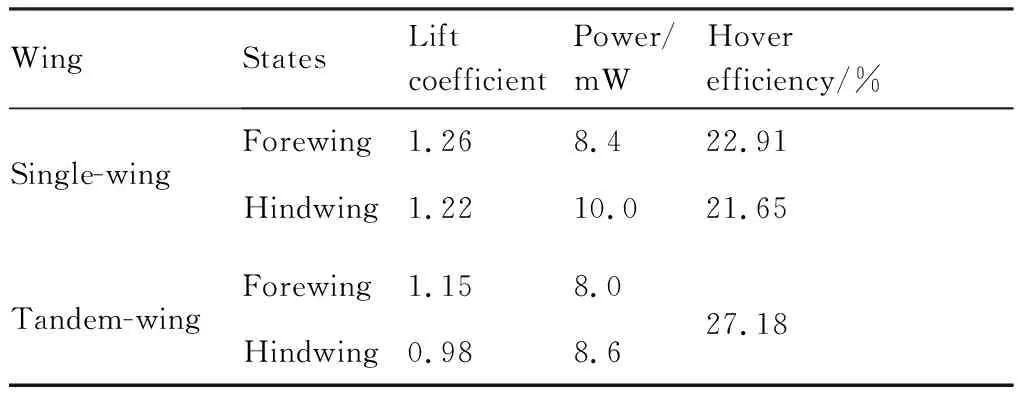
表1 前后翅气动参数

2.2 尾迹集中效应的影响

通过对单翅悬停和双翅悬停的流场进行分析，得到翼间干涉产生上述影响的两个气动机制：尾迹集中机制和来流偏折机制。下面将通过对比双翅拍动和单翅拍动中的后翅流场，对这两个机制进行说明。

由于后翅在T=0.7～0.9时翼间干涉影响明显，因此选择T=0.8时单翅下拍和双翅下拍过程中后翅r2截面的流线进行分析。如图7(a)所示，T=0.8时，单翅下拍翅膀的运动带动周围的空气在翅膀的前缘和尾缘附近部分气流形成涡旋(红色虚线框所示)。涡旋不能提供垂升力，并且气流的耗散会造成能量损失，不利于提高悬停效率。在双翅拍动中，当前后翅靠近时，两翅之间产生的高压区可以消除两翅之间的涡旋，并使原本形成涡旋的气流向下流动，有利于减少能量耗散，提高悬停效率。前翅与后翅相对位置较远时(T=0.4)，前翅对后翅流动的影响较弱。但通过图7(b)T=0.4时刻单翅拍动和双翅拍动的流线对比可以看出，由于前翅对后翅流场存在“阻塞”作用，可以使后翅产生的涡旋强度减弱。通过对图7(c)拍动尾迹的气流角度进行对比可以看出，在双翅拍动下，后翅产生的尾迹气流角相对集中，气流角云图中红色区域面积更大，说明尾迹气流更接近垂直(90°)，有利于更好地提供升力；单翅拍动下产生的尾迹相对分散，气流速度的水平分量更大，不利于悬停状态的维持。

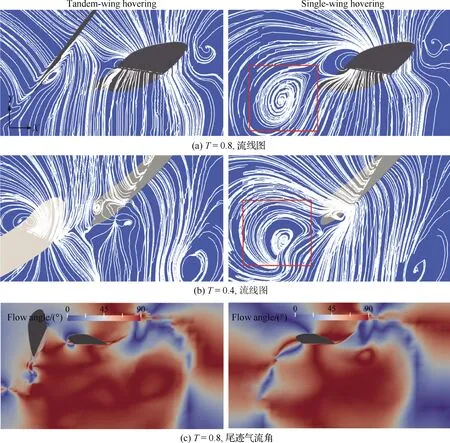
图7 尾迹集中效应流场

综合上述分析，尾迹集中效应总结如下：① 在 双翅拍动下前翅靠近后翅时，两翅之间产生高压区，可以消除涡旋，当两翅远离时，由于前翅的“阻塞”作用，后翅产生的涡流强度也会减弱。② 由于前翅的存在，原本应该产生漩涡的气流向下流动，使尾迹更加集中，垂直向下的速度分量更大。消除漩涡可以减少能量损耗，尾迹集中可以提高悬停的效率。

2.3 来流偏折效应的影响

在翅膀下拍过程中，产生升力的主要来源是附着于翅膀前缘的前缘涡。通过图8中T=0.7，0.8，0.9时刻双翅拍动和单翅拍动的后翅r2界面涡量对比可以看出，双翅拍动的后翅前缘涡尺寸和强度明显减弱。这也解释了图6(c)中T=0.7～0.9期间翼间干涉使后翅下拍过程中升力明显减弱的现象。

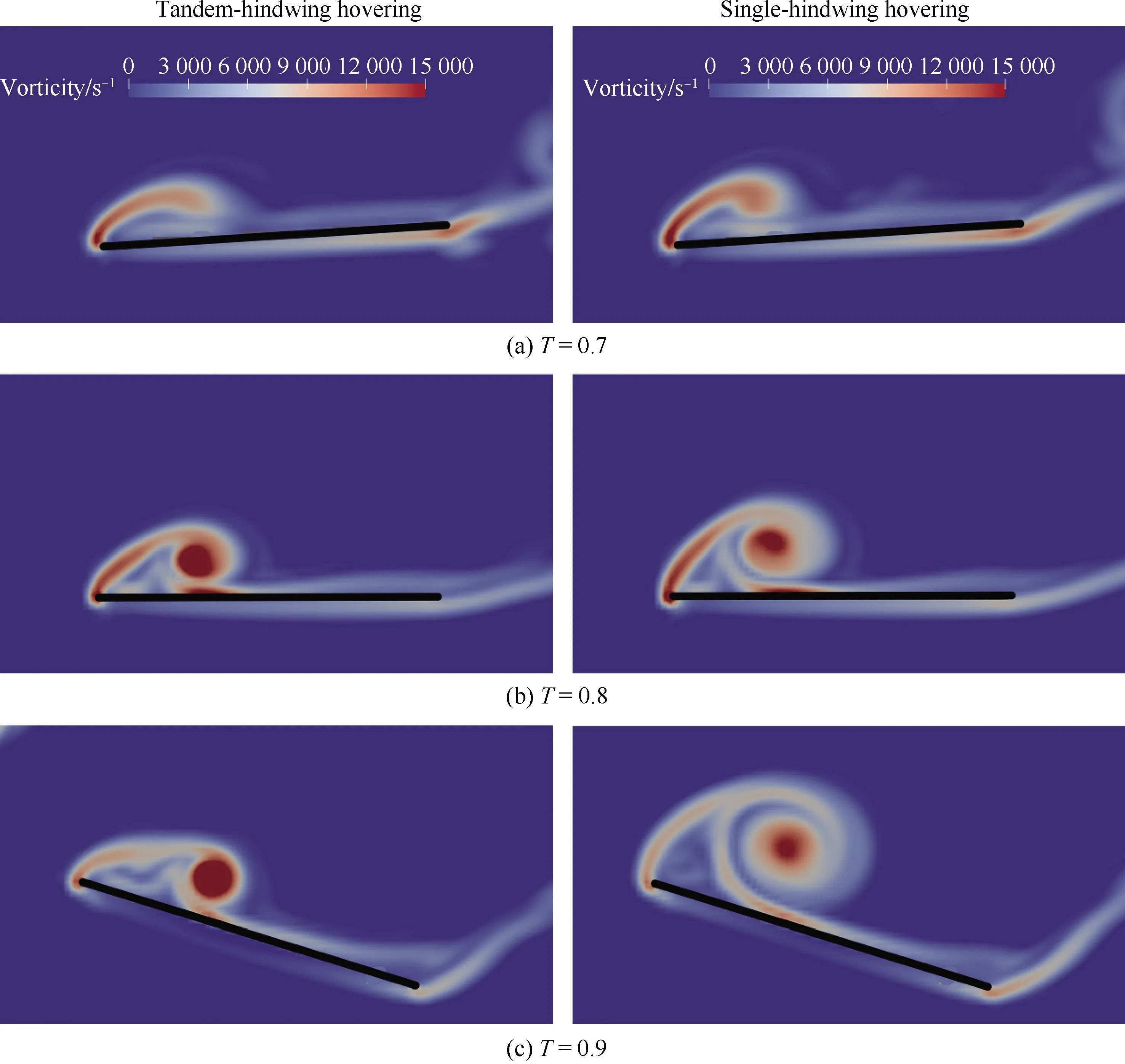
图8 T=0.7,0.8,0.9时刻单独/双翅拍动下后翅涡量图

测量T=0.7，0.8，0.9时刻前缘涡的涡量平均值和涡尺寸，其中涡量平均值为前缘涡范围内平均取点后统计的涡量算数平均值，涡尺寸为前缘涡边缘的最大距离。统计结果如表2所示，可以看出双翅拍动下，翼间干涉减小前缘涡的涡量和尺寸。其中T=0.9时刻减小幅度最大，涡量平均值下降33.8%，前缘涡尺寸下降22.9%。

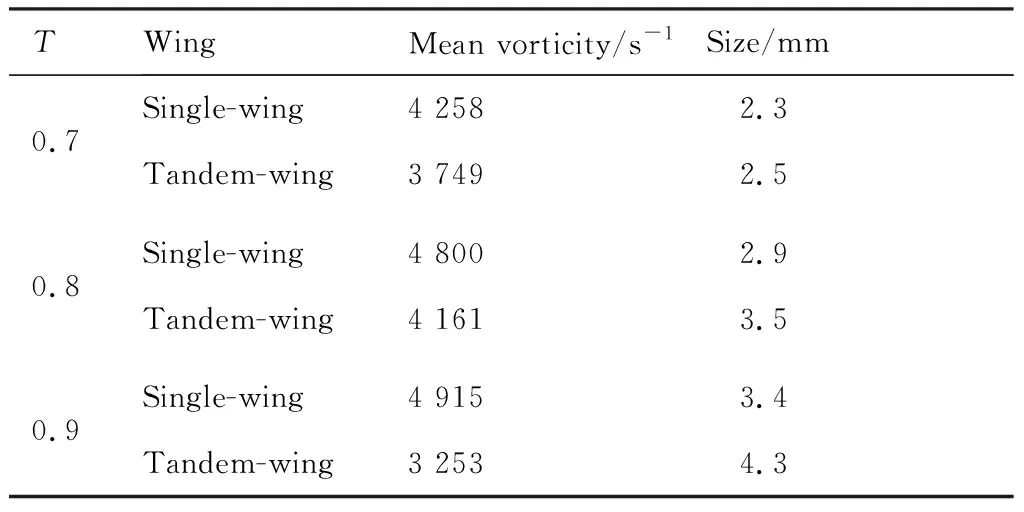
表2 前缘涡平均涡量和尺寸

为了探究翼间干涉减小后翅下拍过程中前缘涡的涡量和尺寸，进而使升力下降的气动机理，提取前缘涡涡量平均值和尺寸下降幅度最大的T=0.9时刻r2截面的流线图进行分析。

从图9(a)对单翅拍动和双翅拍动的流线比较可以看出，在后翅下拍过程中，由于前翅上拍产生的尾迹影响，后翅的来流攻角明显减小。来流攻角的减小会使后翅前缘涡的尺寸、强度和展向流动减弱。

如图9(b)所示，后翅单独拍动时来流的相对速度为V1(蓝色)；双翅拍动中，由于前翅产生向上升力,同时产生向下的尾迹V2(绿色)，两者合成后翅的相对来流速度V3(黑色)。V1和V3的夹角Δα即为尾迹偏折效应使后翅攻角减少的角度。

图9 单/双翅拍动流线图和来流偏折效应流场图

综合上述分析，来流偏折效应总结如下：在后翅下拍过程中，前翅上拍产生的尾迹使得后翅的来流发生偏折，造成后翅来流攻角减小，使前缘涡的展向流动减弱，尺寸和强度相应减小。来流偏折效应带来的前缘涡减弱是翼间干涉造成后翅升力明显减弱的主要原因。需要强调的是，这种气动力上的减弱是蜻蜓通过调节翅膀相位差和运动规律进行的主动、有益的减弱。气动力的减弱可以使蜻蜓在满足悬停状态升力需求的前提下，降低功耗，增加续航。

3 结 论

蜻蜓在悬停状态下利用翼间干涉使双翅拍动下悬停的效率更高，功耗更小。通过对流场进行分析得到翼间干涉改善悬停飞行的两个气动效应，可以为MAV提升续航提供支持。

1)翼间干涉使前翅和后翅的升力系数和气动功率下降，悬停效率上升。前翅升力系数下降8.7%，气动功率下降4.8%，悬停效率提升18.6%；后翅升力下降19.7%，气动功率下降14.0%，悬停效率提升25.5%。翼间干涉下，后翅气动参数的变化幅度大于前翅。由于气动功主要用于提供升力，因此来流偏折效应时气动力下降，气动功率也随之下降。而效率的上升是由于尾迹集中效应减小尾迹中的涡旋耗散引起的。

2)尾迹集中效应通过前后翅的干涉，减弱和消除不利于悬停飞行的涡旋，并使原本产生涡旋的气流向下流动，使尾迹更加集中，垂直向下的速度分量更大，有利于提高悬停效率。

3)来流偏折效应通过前翅对后翅来流的偏折作用，减弱后翅下拍过程中的攻角，使得后翅产生的前缘涡减弱。来流偏折效应减小翅产生的升力，降低所需功耗。